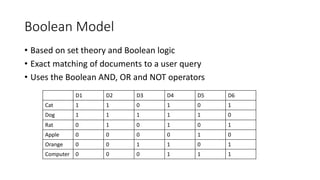
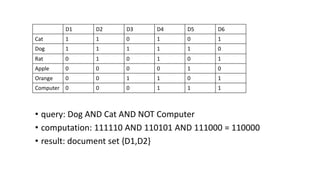
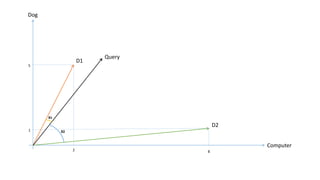
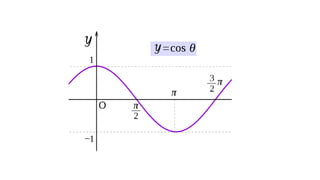
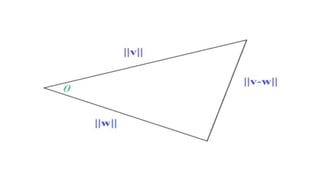
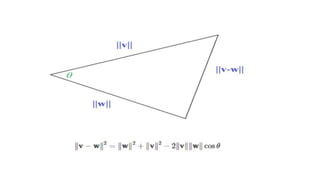
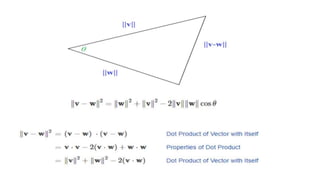
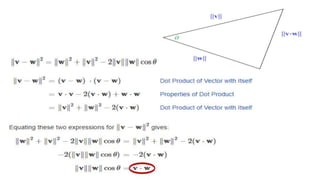
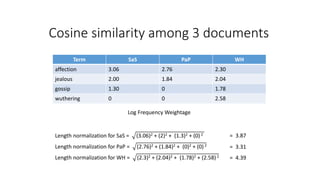
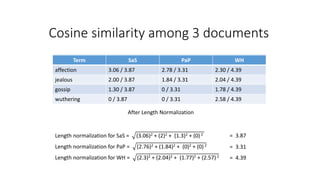
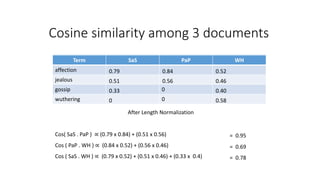
The document compares the Boolean model and the vector space model for information retrieval. The Boolean model emphasizes exact matching using Boolean operators but lacks ranking and synonymy considerations, while the vector space model represents documents and queries as vectors, allowing for similarity computation through cosine similarity. Both models have advantages and disadvantages in terms of implementation, scalability, and processing speed.

1. Vector Space Model
By: Tharuka Vishwajith

2. Boolean Model
• Based on set theory and Boolean logic
• Exact matching of documents to a user query
• Uses the Boolean AND, OR and NOT operators
D1 D2 D3 D4 D5 D6
Cat 1 1 0 1 0 1
Dog 1 1 1 1 1 0
Rat 0 1 0 1 0 1
Apple 0 0 0 0 1 0
Orange 0 0 1 1 0 1
Computer 0 0 0 1 1 1

3. • query: Dog AND Cat AND NOT Computer
• computation: 111110 AND 110101 AND 111000 = 110000
• result: document set {D1,D2}
D1 D2 D3 D4 D5 D6
Cat 1 1 0 1 0 1
Dog 1 1 1 1 1 0
Rat 0 1 0 1 0 1
Apple 0 0 0 0 1 0
Orange 0 0 1 1 0 1
Computer 0 0 0 1 1 1

4. Boolean Model ...
Advantages
• Relatively easy to implement and scalable
• Fast query processing based on parallel scanning of indexes
Disadvantages
• Does not pay attention to synonymy
• Does not pay attention to polysemy
• No ranking of output
• Often the user has to learn a special syntax such as the use of double quotes to
search for phrases

5. Vector Space Model
• Algebraic model representing text documents and queries as vectors
based on the index terms
• One dimension for each term
• Compute the similarity (angle) between the query vector and the
document vectors

6. Dog
Computer
D2
D1
5
1
2 8
Query
θ1
θ2

12. Cosine similarity among 3 documents
Term SaS PaP WH
affection 115 58 20
jealous 10 7 11
gossip 2 0 6
wuthering 0 0 38
1 + log(tf)
Term frequency (tf) count
Log normalization:

13. Cosine similarity among 3 documents
Term SaS PaP WH
affection 115 58 20
jealous 10 7 11
gossip 2 0 6
wuthering 0 0 38
Log Frequency Weightage
Length normalization for SaS = (3.06)2 + (2)2 + (1.3)2 + (0) 2
Term SaS PaP WH
affection 3.06 0.83 0.52
jealous 2.00 0.55 0.46
gossip 1.30 0 0.40
wuthering 0 0 0.58
Length normalization for PaP = (2.76)2 + (1.84)2 + (0)2 + (0) 2
Length normalization for WH = (2.3)2 + (2.04)2 + (1.78)2 + (2.58) 2
= 3.87
= 3.31
= 4.39
Term SaS PaP WH
affection 3.06 2.76 2.30
jealous 2.00 1.84 2.04
gossip 1.30 0 1.78
wuthering 0 0 2.58

14. Cosine similarity among 3 documents
Term SaS PaP WH
affection 115 58 20
jealous 10 7 11
gossip 2 0 6
wuthering 0 0 38
After Length Normalization
Length normalization for SaS = (3.06)2 + (2)2 + (1.3)2 + (0) 2
Term SaS PaP WH
affection 3.06 / 3.87 2.78 / 3.31 2.30 / 4.39
jealous 2.00 / 3.87 1.84 / 3.31 2.04 / 4.39
gossip 1.30 / 3.87 0 / 3.31 1.78 / 4.39
wuthering 0 / 3.87 0 / 3.31 2.58 / 4.39
Length normalization for PaP = (2.76)2 + (1.84)2 + (0)2 + (0) 2
Length normalization for WH = (2.3)2 + (2.04)2 + (1.77)2 + (2.57) 2
= 3.87
= 3.31
= 4.39

15. Cosine similarity among 3 documents
Term SaS PaP WH
affection 115 58 20
jealous 10 7 11
gossip 2 0 6
wuthering 0 0 38
After Length Normalization
Cos( SaS . PaP ) ∝ (0.79 x 0.84) + (0.51 x 0.56)
Term SaS PaP WH
affection 0.79 0.84 0.52
jealous 0.51 0.56 0.46
gossip 0.33 0 0.40
wuthering 0 0 0.58
Cos ( PaP . WH ) ∝ (0.84 x 0.52) + (0.56 x 0.46)
Cos ( SaS . WH ) ∝ (0.79 x 0.52) + (0.51 x 0.46) + (0.33 x 0.4)
= 0.95
= 0.69
= 0.78