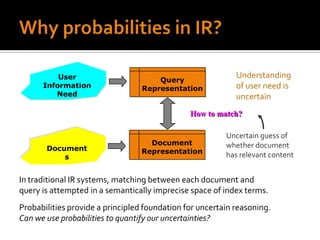
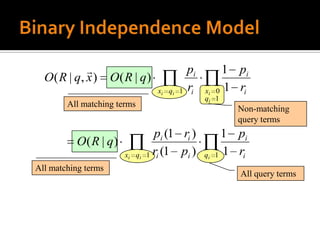
The document discusses probabilistic information retrieval and Bayesian approaches. It introduces concepts like conditional probability, Bayes' theorem, and the probability ranking principle. It explains how probabilistic models estimate the probability of relevance between a document and query by representing them as term sets and making probabilistic assumptions. The goal is to rank documents by the probability of relevance to present the most likely relevant documents first.

1. Ahmet Selman Bozkır

2.  Introduction to conditional, total probability & Bayesian
theorem
 Historical background of probabilistic information retrieval
 Why probabilities in IR?
 Document ranking problem
 Binary Independence Model

3.  Given some event B with nonzero probability P(B) > 0
 We can define conditional prob. as an event A, given B, by
P( A B)
P( A B)
P( B)
The Probabilty P(A|B) simply reflects the fact that the probability of an
event A may depend on a second event B. So if A and B are mutually
exclusive, A B =

4. Tolerance Let’s define three events:
Resistance 5% 10% Total 1. A as “draw 47 resistor
( ) 2. B as “draw” a resistor with 5%
22- 3. C as “draw” a “100 resistor
10 14 24
47- 28 26 44
P(A) = P(47 ) = 44/100
100- 24 8 32 P(B) = P(5%) = 62/100
Total: 62 38 100 P(C) = P(100 ) = 32 /100
The joint probabilities are:
P(A B) = P(47 5%) = 28/100
P(A C) = P(47 100 ) = 0 P( A C )
P( A C ) 0
P(B C) = P(5% 100 ) = 24/100 P(C )
P( A B) 28 P( B C ) 24
I f we use them the cond. prob. : P( A B) P( B C )
P( B) 62 P(C ) 32

5.  The probability of P(A) of any event A defined on a sample space S can be
expressed in terms of cond. probabilities. Suppose we are given N
mutually exclusive events Bn ,n = 1,2…. N whose union equals S as
ilustrated in figure
A Bn
B1 B2
A N N
A S A B
n 1
n (A  B )
n 1
n
B3 Bn

6.  The definition of conditional probability applies to any two
events. In particular ,let Bn be one of the events defined
above in the subsection on total probability.
P(Bn A)
P( Bn A)
P(A)
İf P(A)≠O,or, alternatively,
P( A Bn )
P( A Bn )
P( Bn )

7.  if P(Bn)≠0, one form of Bayes’ theorem is obtained by
equating these two expressions:
P( A Bn ) P( Bn )
P( Bn A)
P( A)
 Another form derives from a substitution of P(A) as given:
P( A Bn ) P( Bn )
P( Bn A)
P( A B1 ) P( B1 ) ... P( A BN ) P( BN )

8.  The first attempts to develop a probabilistic theory of retrieval were made over
30 years ago [Maron and Kuhns 1960; Miller 1971], and since then there has been
a steady development of the approach. There are already several operational IR
systems based upon probabilistic or semiprobabilistic models.
 One major obstacle in probabilistic or semiprobabilistic IR models is finding
methods for estimating the probabilities used to evaluate the probability of
relevance that are both theoretically sound and computationally efficient.
 The first models to be based upon such assumptions were the “binary
independence indexing model” and the “binary independence retrieval model
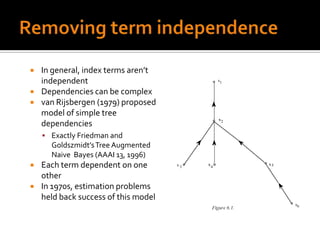
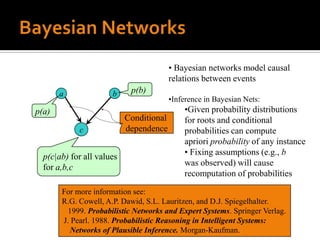
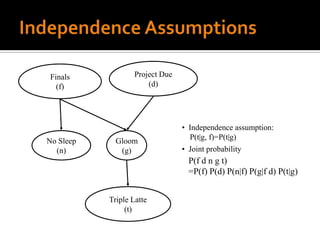
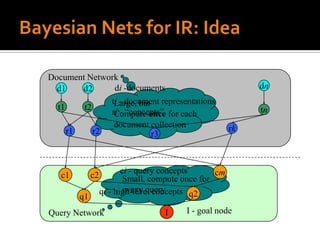
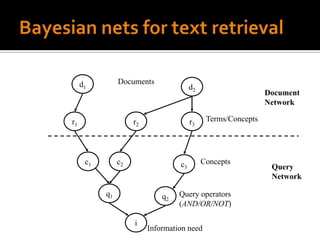
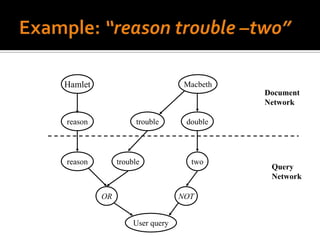
 One area of recent research investigates the use of an explicit network
representation of dependencies. The networks are processed by means of
Bayesian inference or belief theory, using evidential reasoning techniques such as
those described by Pearl 1988. This approach is an extension of the earliest
probabilistic models, taking into account the conditional dependencies present in
a real environment.

9. User Understanding
Query
Information Representation of user need is
Need uncertain
How to match?
Uncertain guess of
Document whether document
Document Representation
s has relevant content
In traditional IR systems, matching between each document and
query is attempted in a semantically imprecise space of index terms.
Probabilities provide a principled foundation for uncertain reasoning.
Can we use probabilities to quantify our uncertainties?

10.  Classical probabilistic retrieval model
 Probability ranking principle, etc.
 (Naïve) Bayesian Text Categorization
 Bayesian networks for text retrieval
 Probabilistic methods are one of the oldest but also one of the
currently hottest topics in IR.
 Traditionally: neat ideas, but they’ve never won on
performance. It may be different now.

11.  In probabilistic information retrieval, the goal is the estimation of the
probability of relevance P(R l qk, dm) that a document dm will be judged
relevant by a user with request qk. In order to estimate this probability, a
large number of probabilistic models have been developed.
 Typically, such a model is based on representations of queries and
documents (e.g., as sets of terms); in addition to this, probabilistic
assumptions about the distribution of elements of these representations
within relevant and nonrelevant documents are required.
 By collecting relevance feedback data from a few documents, the model
then can be applied in order to estimate the probability of relevance for
the remaining documents in the collection.

12.  We have a collection of documents
 User issues a query
 A list of documents needs to be returned
 Ranking method is core of an IR system:
 In what order do we present documents to the
user?
 We want the “best” document to be first, second best
second, etc….
 Idea: Rank by probability of relevance of the
document w.r.t. information need
 P(relevant|documenti, query)

13.  For events a and b:
 Bayes’ Rule
p(a, b) p(a b) p(a | b) p (b) p (b | a) p (a )
p(a | b) p(b) p (b | a ) p (a )
Prior
p(b | a) p(a) p(b | a) p(a)
p ( a | b)
Posterior
p (b) x a ,a
p (b | x) p( x)
 Odds: p(a) p(a)
O(a )
p(a ) 1 p(a)

14. Let x be a document in the collection.
Let R represent relevance of a document w.r.t. given (fixed)
query and let NR represent non-relevance.
R={0,1} vs. NR/R
Need to find p(R|x) - probability that a document x is relevant.
p( x | R) p( R) p(R),p(NR) - prior probability
p( R | x) of retrieving a (non) relevant
p( x) document
p( x | NR) p( NR)
p( NR | x)
p ( x) p ( R | x) p( NR | x) 1
p(x|R), p(x|NR) - probability that if a relevant (non-relevant) document is
retrieved, it is x.

15.  Bayes’ Optimal Decision Rule
 x is relevant iff p(R|x) > p(NR|x)
 PRP in action: Rank all documents by p(R|x)

16.  More complex case: retrieval costs.
 Let d be a document
 C - cost of retrieval of relevant document
 C’ - cost of retrieval of non-relevant document
 Probability Ranking Principle: if
C p( R | d ) C (1 p( R | d )) C p( R | d ) C (1 p( R | d ))
for all d’ not yet retrieved, then d is the next
document to be retrieved
 We won’t further consider loss/utility from
now on

17.  How do we compute all those probabilities?
 Do not know exact probabilities, have to use
estimates
 Binary Independence Retrieval (BIR) – which we
discuss later today – is the simplest model
 Questionable assumptions
 “Relevance” of each document is independent of
relevance of other documents.
▪ Really, it’s bad to keep on returning duplicates
 Boolean model of relevance

18.  Estimate how terms contribute to relevance
 How tf, df, and length influence your judgments
about do things like document relevance?
▪ One answer is the Okapi formulae (S. Robertson)
 Combine to find document relevance
probability
 Order documents by decreasing probability

19.  Basic concept:
 "For a given query, if we know some documents
that are relevant, terms that occur in those
documents should be given greater weighting in
searching for other relevant documents.
 By making assumptions about the distribution of
terms and applying Bayes Theorem, it is possible
to derive weights theoretically."
 Van Rijsbergen

20.  Traditionally used in conjunction with PRP
 “Binary” = Boolean: documents are represented as binary
incidence vectors of terms (cf. lecture 1):

 x ( x1 , , xn )
 xi 1 iff term i is present in document x.
 “Independence”: terms occur in documents independently
 Different documents can be modeled as same vector
 Bernoulli Naive Bayes model (cf. text categorization!)

21.  Queries: binary term incidence vectors
 Given query q,
 for each document d need to compute p(R|q,d).
 replace with computing p(R|q,x) where x is binary term
incidence vector representing d Interested only in
ranking
 Will use odds and Bayes’ Rule:

p ( R | q ) p ( x | R, q )
 
 p ( R | q, x ) p( x | q)
O ( R | q, x )  
p( NR | q, x ) p( NR | q) p( x | NR, q)

p( x | q)

22.  
 p ( R | q, x ) p ( R | q ) p ( x | R, q )
O ( R | q, x )  
p( NR | q, x ) p( NR | q) p( x | NR, q)
Constant for a
Needs estimation
given query
• Using Independence Assumption:
 n
p ( x | R, q ) p ( xi | R, q )

p ( x | NR, q ) i 1 p ( xi | NR, q )
n
•So : p ( xi | R, q )
O ( R | q, d ) O( R | q)
i 1 p ( xi | NR , q )

23. n
p ( xi | R, q )
O ( R | q, d ) O( R | q)
i 1 p ( xi | NR, q )
• Since xi is either 0 or 1:
p( xi 1 | R, q) p( xi 0 | R, q)
O( R | q, d ) O( R | q)
xi 1 p( xi 1 | NR, q) xi 0 p( xi 0 | NR, q)
• Let pi p( xi 1 | R, q); ri p( xi 1 | NR, q);
• Assume, for all terms not occurring in the query (qi=0) pi ri
This can be
changed (e.g., in
Then... relevance feedback)

24.  pi 1 pi
O ( R | q, x ) O( R | q)
xi qi 1 ri xi 0 1 ri
qi 1
All matching terms
Non-matching
query terms
pi (1 ri ) 1 pi
O( R | q)
xi qi 1 ri (1 pi ) qi 1 1 ri
All matching terms
All query terms

25.  pi (1 ri ) 1 pi
O ( R | q, x ) O ( R | q )
xi q i 1 ri (1 pi ) qi 1 1 ri
Constant for
each query
Only quantity to be estimated
for rankings
• Retrieval Status Value:
pi (1 ri ) pi (1 ri )
RSV log log
xi qi 1 ri (1 pi ) xi qi 1 ri (1 pi )

26. • Estimating RSV coefficients.
• For each term i look at this table of document counts:
Documens Relevant Non-Relevant Total
Xi=1 s n-s n
Xi=0 S-s N-n-S+s N-n
Total S N-S N
s (n s)
• Estimates: pi ri
S (N S) For now,
s (S s) assume no
ci K ( N , n, S , s ) log zero terms.
(n s) ( N n S s)

27.  If non-relevant documents are approximated by the whole
collection, then ri (prob. of occurrence in non-relevant
documents for query) is n/N and
 log (1– ri)/ri = log (N– n)/n ≈ log N/n = IDF!
 pi (probability of occurrence in relevant documents) can be
estimated in various ways:
 from relevant documents if know some
▪ Relevance weighting can be used in feedback loop
 constant (Croft and Harper combination match) – then just get idf
weighting of terms
 proportional to prob. of occurrence in collection
▪ more accurately, to log of this (Greiff, SIGIR 1998)

28. 1. Assume that pi constant over all xi in query
 pi = 0.5 (even odds) for any given doc
2. Determine guess of relevant document set:
 V is fixed size set of highest ranked documents on
this model (note: now a bit like tf.idf!)
3. We need to improve our guesses for pi and ri, so
 Use distribution of xi in docs in V. Let Vi be set of
documents containing xi
▪ pi = |Vi| / |V|
 Assume if not retrieved then not relevant
▪ ri = (ni – |Vi|) / (N – |V|)
4. Go to 2. until converges then return ranking

29. 1. Guess a preliminary probabilistic description of R
and use it to retrieve a first set of documents
V, as above.
2. Interact with the user to refine the description:
learn some definite members of R and NR
3. Reestimate pi and ri on the basis of these
 Or can combine new information with original guess
(use Bayesian prior): | Vi | pi(1)
pi( 2 ) κ is
|V | prior
4. Repeat, thus generating a succession of weight
approximations to R.

30.  Getting reasonable approximations of
probabilities is possible.
 Requires restrictive assumptions:
 term independence
 terms not in query don’t affect the outcome
 boolean representation of documents/queries/relevance
 document relevance values are independent
 Some of these assumptions can be removed
 Problem: either require partial relevance information or
only can derive somewhat inferior term weights

31.  In general, index terms aren’t
independent
 Dependencies can be complex
 van Rijsbergen (1979) proposed
model of simple tree
dependencies
 Exactly Friedman and
Goldszmidt’s Tree Augmented
Naive Bayes (AAAI 13, 1996)
 Each term dependent on one
other
 In 1970s, estimation problems
held back success of this model

32.  What is a Bayesian network?
 A directed acyclic graph
 Nodes
▪ Events or Variables
▪ Assume values.
▪ For our purposes, all Boolean
 Links
▪ model direct dependencies between nodes

33. • Bayesian networks model causal
relations between events
a b p(b)
•Inference in Bayesian Nets:
p(a) •Given probability distributions
Conditional for roots and conditional
c dependence probabilities can compute
apriori probability of any instance
• Fixing assumptions (e.g., b
p(c|ab) for all values
was observed) will cause
for a,b,c
recomputation of probabilities
For more information see:
R.G. Cowell, A.P. Dawid, S.L. Lauritzen, and D.J. Spiegelhalter.
1999. Probabilistic Networks and Expert Systems. Springer Verlag.
J. Pearl. 1988. Probabilistic Reasoning in Intelligent Systems:
Networks of Plausible Inference. Morgan-Kaufman.

34. f 0 .3 Project Due d 0.4
Finals
f 0 .7 (f) (d) d 0.6
f f fd fd f d f d
n 0.9 0.3 No Sleep Gloom g 0.99 0.9 0.8 0.3
(n) (g)
n 0.1 0.7 g 0.01 0.1 0.2 0.7
g g Triple Latte
t 0.99 0.1 (t)
t 0.01 0.9

35. Finals Project Due
(f) (d)
• Independence assumption:
No Sleep Gloom P(t|g, f)=P(t|g)
(n) (g) • Joint probability
P(f d n g t)
=P(f) P(d) P(n|f) P(g|f d) P(t|g)
Triple Latte
(t)

36.  Goal
 Given a user’s information need (evidence), find
probability a doc satisfies need
 Retrieval model
 Model docs in a document network
 Model information need in a query network

37. Document Network
d1 d2 di -documents dn
ti - document representations
Large, but
t1 t2 tn
ri - “concepts” for each
Compute once
document collection rk
r1 r2 r3
ci - query concepts cm
c1 c2 Small, compute once for
every query
qi - high-level concepts q2
q1
Query Network I I - goal node

38.  Construct Document Network (once !)
 For each query
 Construct best Query Network
 Attach it to Document Network
 Find subset of di’s which maximizes the
probability value of node I (best subset).
 Retrieve these di’s as the answer to query.

39. d1 Documents
d2
Document
Network
r1 r2 r3 Terms/Concepts
c1 c2 c3 Concepts
Query
Network
q1 q2 Query operators
(AND/OR/NOT)
i
Information need

40.  Prior doc probability P(d) =  P(c|r)
1/n  1-to-1
 P(r|d)  thesaurus
 within-document term  P(q|c): canonical forms of
frequency query operators
 tf idf - based  Always use things like AND
and NOT – never store a
full CPT*
*conditional probability table

41. Hamlet Macbeth
Document
Network
reason trouble double
reason trouble two
Query
Network
OR NOT
User query

42.  Prior probs don’t have to be 1/n.
 “User information need” doesn’t have to be a
query - can be words typed, in docs read, any
combination …
 Phrases, inter-document links
 Link matrices can be modified over time.
 User feedback.
 The promise of “personalization”

43.  Document network built at indexing time
 Query network built/scored at query time
 Representation:
 Link matrices from docs to any single term are like
the postings entry for that term
 Canonical link matrices are efficient to store and
compute
 Attach evidence only at roots of network
 Can do single pass from roots to leaves

44. All sources served by Google!