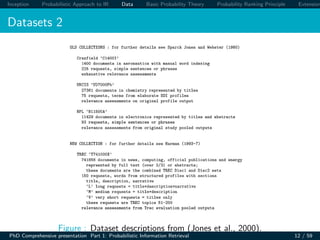
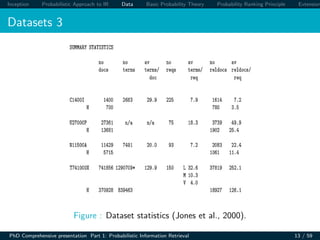
The document presents an overview of probabilistic models for information retrieval. It discusses how probability theory can be applied to model the uncertain nature of retrieval, where queries only vaguely represent user needs and relevance is uncertain. The document outlines different probabilistic IR models including the classical probabilistic retrieval model, probability ranking principle, binary independence model, Bayesian networks, and language modeling approaches. It also describes datasets used to evaluate these models, including collections from TREC, Cranfield, and others. Basic probability theory concepts are reviewed, including joint probability, conditional probability, and rules relating probabilities.





































































![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Probability Ranking Principle (PRP)
PRP in brief
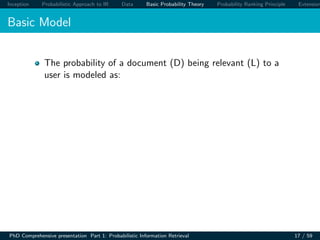
If the retrieved documents (w.r.t a query) are ranked
decreasingly on their probability of relevance, then the
effectiveness of the system will be the best that is obtainable
PRP in full
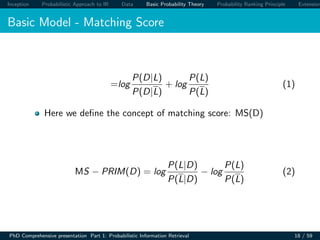
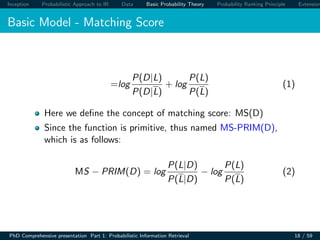
If [the IR] system’s response to each [query] is a ranking of the
documents [...] in order of decreasing probability of relevance
to the [query], where the probabilities are estimated as
accurately as possible on the basis of whatever data have been
made available to the system for this purpose, the overall
effectiveness of the system to its user will be the best that is
obtainable on the basis of those data
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 26 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-88-320.jpg)























































![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
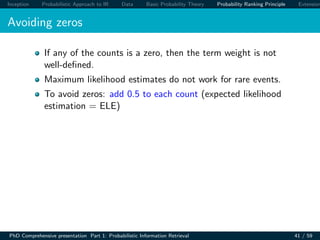
Simplifying assumption
Assuming that relevant documents are a very small
percentage of the collection, approximate statistics for
nonrelevant documents by statistics from the whole collection
Hence, (pt) (the probability of term occurrence in nonrelevant
documents for a query) is n/N and
log[(1 − (pt))/(pt)] = log[(N − n)/n] ≈ log N/n
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 42 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-149-320.jpg)
![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Simplifying assumption
Assuming that relevant documents are a very small
percentage of the collection, approximate statistics for
nonrelevant documents by statistics from the whole collection
Hence, (pt) (the probability of term occurrence in nonrelevant
documents for a query) is n/N and
log[(1 − (pt))/(pt)] = log[(N − n)/n] ≈ log N/n
The above approximation cannot easily be extended to
relevant documents
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 42 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-150-320.jpg)





























![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Okapi BM25 Basic Weighting
Improve idf term [log N/n] by factoring in term frequency and
document length.
RSVd =
t∈q
log
N
n
·
(k1 + 1)tftd
k1((1 − b) + b × (Ld /Lave)) + tftd
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 50 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-188-320.jpg)
![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Okapi BM25 Basic Weighting
Improve idf term [log N/n] by factoring in term frequency and
document length.
RSVd =
t∈q
log
N
n
·
(k1 + 1)tftd
k1((1 − b) + b × (Ld /Lave)) + tftd
tftd : term frequency in document d
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 50 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-189-320.jpg)
![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Okapi BM25 Basic Weighting
Improve idf term [log N/n] by factoring in term frequency and
document length.
RSVd =
t∈q
log
N
n
·
(k1 + 1)tftd
k1((1 − b) + b × (Ld /Lave)) + tftd
tftd : term frequency in document d
Ld (Lave): length of document d (average document length in
the whole collection)
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 50 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-190-320.jpg)
![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Okapi BM25 Basic Weighting
Improve idf term [log N/n] by factoring in term frequency and
document length.
RSVd =
t∈q
log
N
n
·
(k1 + 1)tftd
k1((1 − b) + b × (Ld /Lave)) + tftd
tftd : term frequency in document d
Ld (Lave): length of document d (average document length in
the whole collection)
k1: tuning parameter controlling the document term
frequency scaling
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 50 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-191-320.jpg)
![Inception Probabilistic Approach to IR Data Basic Probability Theory Probability Ranking Principle Extension
Okapi BM25 Basic Weighting
Improve idf term [log N/n] by factoring in term frequency and
document length.
RSVd =
t∈q
log
N
n
·
(k1 + 1)tftd
k1((1 − b) + b × (Ld /Lave)) + tftd
tftd : term frequency in document d
Ld (Lave): length of document d (average document length in
the whole collection)
k1: tuning parameter controlling the document term
frequency scaling
b: tuning parameter controlling the scaling by document
length
PhD Comprehensive presentation Part 1: Probabilistic Information Retrieval 50 / 59](https://image.slidesharecdn.com/probabilisticirv1-150805205610-lva1-app6891/85/Probabilistic-Information-Retrieval-192-320.jpg)