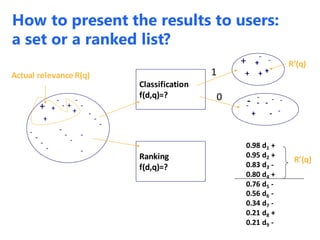
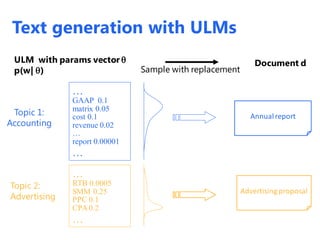
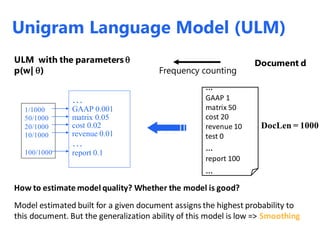
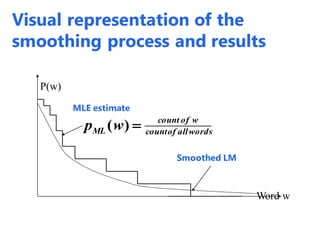
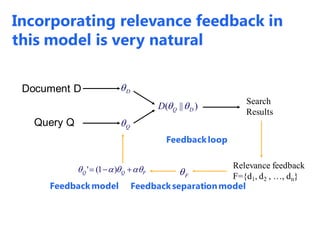
The document discusses statistical language models for information retrieval (IR), covering their historical development and various ranking models including probabilistic approaches. It details methodologies for filtering and ranking documents based on query relevance using vector space models, and emphasizes the evolution of models from classical to advanced statistical methods. Additionally, it examines the concept of text similarity, the use of machine learning in ranking, and evaluates the performance of unigram language models in IR contexts.

1. Statistical Language Models
for Information Retrieval
by: Nik Spirinat:
Disclaimer: The slides are significantly based on the lectures of Prof. ChengXiang Zhai at UIUC
(http://czhai.cs.illinois.edu/). All the credit goes to the author. All the blame is for the presenter.

2. This talk will help
you help people
find jobs! 

3. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

4. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

5. History of Information Retrieval
• 1950 – 1960: early days and first empirical observations
– Hypothesis on automated indexing (Luhn)
– First experiments and development of guidelines for information retrieval
systems evaluation (Cleverdon’s Cranfield 1 and Cranfield 2)
– Early experiments of a Vector Space Model for ranking (Salton’s SMART)
• 1970 – 1980: active development of information retrieval
– Establishment of a Vector Space Model for ranking
– Ranking models based on probability ranking principle (PRP)
• 1990s: further development and formalization of IR (new applications and
theoretical explanations)
– Statistical Language Models (Croft ’98)
– Development of large scale collections for IR systems evaluation (TREC)
• 2000s: web search, large scale search engines in the wild, anti-spam
– Machine Learning to Rank
– MapReduce, GFS, Hadoop…
• 2010s: vertical search, entity search, social search, real-time search

6. Problem formulation
• Given:
– A vocabulary for a natural language ;
– A set of learning queries , where each
word from a query is part of the vocabulary;
– A collection of documents , where
every document is an order sequence of words;
– A set of learning query/document pairs with
relevance judgments
• Deliever:
– A set (ranked list) of documents from a collection
for a new query.

7. How to present the results to users:
a set or a ranked list?
• Strategy 1 (document filtering)
– R(q) = { dC | f(d,q)=1 }, where f(d,q)  {0,1} is a
classifier, indicator function
– The algorithm should predict an absolute
relevance of a document with respect to a query.
• Strategy 2 (document ranking)
– R(q) = { dC | f(d,q)> }, where f(d,q)  is a
raning function;  is a relevance threshold
– The algorithm should predict a relative relevance
of a document with respect to the query and
adjust the threshold.

8. +
+
+ +
-
-
-
-
-
-
-
-
-
-
-
-
-
-
+
-
-
Classification
f(d,q)=?
+
+
+
+
- -
+
-
+
-
-
- -
-
--
-
Ranking
f(d,q)=?
1
0.98 d1 +
0.95 d2 +
0.83 d3 -
0.80 d4 +
0.76 d5 -
0.56 d6 -
0.34 d7 -
0.21 d8 +
0.21 d9 -
R’(q)
R’(q)
Actual relevance R(q)
How to present the results to users:
a set or a ranked list?
0

9. How to present the results to users:
a set or a ranked list?
• Strategy 1 (document filtering)
– R(q) = { dC | f(d,q)=1 }, where f(d,q)  {0,1} is a
classifier, indicator function
– The algorithm should predict an absolute
relevance of a document with respect to a query.
• Strategy 2 (document ranking)
– R(q) = { dC | f(d,q)> }, where f(d,q)  is a
raning function;  is a relevance threshold
– The algorithm should predict a relative relevance
of a document with respect to the query and
adjust the threshold.

10. Models based on text similarity (1)
• Insight:
– A document relevance for a query correlates with
the textual similarity between a document and a
query
• Vector Space Model for ranking(VSM)
– Document and query are represented as vectors
in a metric space (dim ~ |V|);
– Each word in a vocabulary has an associated
weight, which serves as a proxy for the word
informativeness and uniqueness;
– Relevance is a function of vectors similarity.

11. • Document is a vector ;
• Query is a vector ;
• Words are weighted according to TFIDF, which takes
into account:
– Word frequency in a document (TF);
– Word popularity in a collection (IDF);
– Document length;
• Similarity is measured as a normalized scalar
product (cosine similarity).
Models based on text similarity (2)

12. • Advantages:
– Gives the best results among all classical ranking
models;
– Very simple conceptually and implementation-wise;
– There are many collections and benchmarks for
evaluation with the peers;
• Disadvantages:
– Based on heuristics and assumes independence of
words in the query and documents;
– Difficult to extend given a domain knowledge;
– Requires careful parameter tuning by experts;
– Doesn’t explain how to represent queries and
documents and why vectors are good.
Models based on text similarity (3)

13. Probabilistic Ranking Principle, PRP (1)
• Given a training set , construct
a mapping function .
• Define a likelihood function
and a function of a posterior model
parameters

14. • The optimal decision function for a new
object will look like
• Define a loss function s.t. when
and when , and Bayesian risk
then
Probabilistic Ranking Principle, PRP (2)

15. Probabilistic Ranking Models (1)
• Insight:
– What is the probability that a document is
relevant for a query?
• Probabilistic Ranking Model (PRM):
– Consider three random variables (query,
document, relevance R  {0,1});
– Goal: sort the documents in the decreasing order
using probabilistic scores, P(R=1|Q,D);
– There are several major ways to estimate the
probability P(R=1|Q,D).

16. • Discriminative approach (estimate the probability
directly, machine learning to rank):
– Define features on Q x D, like # shared words,
document length, IDF of the most frequent word on a
page, predictions of multiple ranking functions
baseR(Q,D),…
– Using a training set (query, documents, known
relevance judgements on training pairs), tune model
parameters
– For a new case (query/document) pair, generate
features and apply a trained model
Probabilistic Ranking Models (1)

17. • Generative approach (factorize a probability of
relevance into a product of random variables)
– Compute Odds(R=1|Q,D) using Bayes rule
– Define a generative model P(Q,D|R)
• Possible factorization approaches
– Document generation: P(Q,D|R)=P(D|Q,R)P(Q|R)
– Query generation: P(Q,D|R)=P(Q|D,R)P(D|R)
)0(
)1(
)0|,(
)1|,(
),|0(
),|1(
),|1(








RP
RP
RDQP
RDQP
DQRP
DQRP
DQRO
Doesn’t affect ranking
Probabilistic Ranking Models (2)

18. )0,|(
)1,|(
)0|()0,|(
)1|()1,|(
)0|,(
)1|,(
),|0(
),|1(











RQDP
RQDP
RQPRQDP
RQPRQDP
RDQP
RDQP
DQRP
DQRP
Model for relevant document for Q
Model for irrelevant document for Q
Lets assume independence of random variablesT1… Tk
Let D=d1…dk, where dk {0,1} is a set of possiblevalues for Tk (same for Q=q1…qm )
)0),0,|1()1,|1((
)1,|0()0,|1(
)0,|0()1,|1(
)1,|0()0,|1(
)0,|0()1,|1(
)0,|0(
)1,|0(
)0,|1(
)1,|1(
)0,|(
)1,|(
),|0(
),|1(
1,1
1,1
0,11,1
1

























iii
qdi ii
ii
di ii
ii
di i
i
di i
i
i ii
ii
qwhenRQTPRQTPLet
RQTPRQTP
RQTPRQTP
RQTPRQTP
RQTPRQTP
RQTP
RQTP
RQTP
RQTP
RQdTP
RQdTP
DQRP
DQRP
ii
i
ii
Probabilistic Ranking Models (3):
document generation

19. One should estimate 2 parameters for each term Ti:
• pi = P(Ti=1|Q,R=1):probability that Ti is associated with relevant
class of documents;
• qi = P(Ti=1|Q,R=0):probability that Ti is associated with irrelevant
class of documents;
  


1,1 )1(
)1(
log),|1(log
ii qdi ii
ii
Rank
pq
qp
DQRO (RSJ model)
How to estimate these parameters?
1).(#
5.0).(#
ˆ
1).(#
5.0).(#
ˆ






docnonrel
Twithdocnonrel
q
docrel
Twithdocrel
p i
i
i
i
Probabilistic Ranking Models (4):
document generation

20. ))0|()0,|((
)0|(
)1|(
)1,|(
)0|()0,|(
)1|()1,|(
)0|,(
)1|,(
),|1(










RQPRDQPПусть
RDP
RDP
RDQP
RDPRDQP
RDPRDQP
RDQP
RDQP
DQRO
Assuming a uniform documents relevance
Probability of a query p(q| d)
A priori document relevance
)1,|(),|1(  RDQPDQRO
How to estimate query probability given a document? )1,|( RDQP
The approach consists of 2 stages:
• Build a language model for each document D
• Compute relevance of documents for the query.
Probabilistic Ranking Models (5):
query generation

21. Other classical IR models
• Ranking based on graphical models
– Insight: using a full Bayesian inference derive the
relevance of a document for a query
• Ranking based on genetic algorithms and
symbolic regression
– Insight: generate, test, pick the most promising
• Full empirical risk minimization
• Heuristic approach based on structural
properties of a ranking function

22. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

23. Statistical Language Models (def)
• Probabilistic distribution on word sequences:
– p(“I love Indeed”)  0.001;
– p(“Gramm matrix in a Unitarian space is
Hermitian”)  0.0000000000001;
– p(“I beat Google”)  0.00001.
• It can be used to generate texts and
sentences => also referred to as a generative
language model.
• Depends on a collection, language, type of
model, params, training procedure..

24. Statistical Language Models
(examples of application)
• Allows to analyze and describe language using
an abstract theoretical model.
• Using SLM one can answer:
– For a phrase “Responsible for”, predict the probability that the next work
will be “analysis”? What about “sales”? May be “coffee”?
(speech recognition, machine translation)
– If the word “Big” is observed 1 per job posting and “Data” 7 times, what
is the probabilitythat the job posting is about a Data Scientist job?
(information retrieval, text categorization)
– If a person applies for accountant, what is the probabilitythat s/he will
use the phrase “attention to details” in the resume?
(informationretrieval using language models)

25. • Texts is generated sequentially using
sampling with replacement such that words
in the sequence are independent.
– p(w1 w2 ... wn)=p(w1)p(w2)…p(wn).
• Model parameters {p(wi)} must follow
p(w1)+…+p(wN)=1, where N = |V|.
• Formally, ULM represents a multinomial
distribution on the set of words.
Unigram Language Model (ULM)

26. ULM with params vector 
p(w| )
…
GAAP 0.1
matrix 0.05
cost 0.1
revenue 0.02
…
report 0.00001
…
Topic 1:
Accounting
…
RTB 0.0005
SMM 0.25
PPC 0.1
CPA 0.2
…
Topic 2:
Advertising
Document d
Annualreport
Advertising proposal
Sample with replacement
Text generation with ULMs

27. ULM with the parameters 
p(w| )
Document d
Frequency counting
…
GAAP 1
matrix 50
cost 20
revenue 10
test 0
…
report 100
…
DocLen = 1000
1/1000
50/1000
20/1000
10/1000
100/1000
…
GAAP 0.001
matrix 0.05
cost 0.02
revenue 0.01
…
report 0.1
How to estimate model quality? Whether the model is good?
Model estimated built for a given document assigns the highest probability to
this document. But the generalization ability of this model is low => Smoothing
Unigram Language Model (ULM)

28. Evaluation of SLMs
• Direct: How good the model predicts the data?
– Examples: likelihood, perplexity, cross-entropy, KL-
divergence (equivalents of each other under simple
transformations)
• Indirect: Does this model lead to improvements in the final
application (translation, search,..)?
– Domain-dependent external metric. In case of information
retrieval we measure the improvements in quality, which in
turn is estimated via heuristic metrics, like DCG, MRR, MAP.
– Assumption: more accurate linguistic model leads to
better search quality, but not always!
Evaluation of SLMs

29. • N-gram model
– p(w1 w2 ... wn)=p(w1)p(w2|w1)…p(wn|w1 …wn-1);
– n-gram means that the generation process depends on
the last n-1 words;
– For example, the bi-gram model has the following form:
p(w1 ... wn)=p(w1)p(w2|w1) p(w3|w2) …p(wn|wn-1).
• Models taking into account long range dependencies
between words (Maximum Entropy Language Model..)
• Structured language models (probabilistic context-
free grammar, PCFG).
• Most of the time in information retrieval we use
only a Unigram Language Model.
More complex SLMs

30. Why only Unigram Language Models?
• Computational challenge to use more complex
models:
– Need to tune more parameters => need more data to
combat data scarcity problems (e.g. model trained on
100 documents is far from useful).
– Lead to increase in query latencies and storage cost.
• The most important aspect from IR perspective is
to capture topical relevance. Not the case for IE.
• But the application of more complex models
should finally lead to the increase in search
quality and we hope to see more of this in the
future.

31. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

32. Document
Job posting for
data scientist
Job posting for
product manager
Language model
…
text ?
mining ?
analysis?
Bayes ?
…
hadoop?
…
…
product?
launch?
customer?
prioritization?
…
Query: Q = “Hadoop”
Which model most likely
generated this query
Basic ranking model based on statistical
language models (1)

33. d1
d2
dN
qd1
d2
dN
LMs documents
p(q| d1
)
p(q| d2
)
p(q| dN
)
Query likelihood
…
2 key questions:
• Which language model we should use?
• How to effectively estimate parameters for all models di
?
Basic ranking model based on statistical
language models (2)

34. • Multi-Bernoulli: presence/absence of words
– q= (x1, …, x|V|), xi =1 если слово wi есть в документе; xi =0 если нет;
– Параметры: { p(wi=1|d), p(wi=0|d)}, так что p(wi=1|d)+ p(wi=0|d) = 1.
• Multinomial (ULM): words frequency model
– Q = q1,…qm , where qj is a word form the query
– c(wi,q) is the word frequency wi in a query Q
– Parameters: {p(wi|d)} such that p(w1|d)+… p(w|v||d) = 1.
| | | | | |
1 | |
1 1, 1 1, 0
( ( ,..., ) | ) ( | ) ( 1| ) ( 0| )
i i
V V V
V i i i i
i i x i x
p q x x d p w x d p w d p w d
    
       
| |
( , )
1
1 1
( ... | ) ( | ) ( | ) i
Vm
c w q
m j i
j i
p q q q d p q d p w d
 
   
Practically, multinomial model is the best according to multiple benchmarks
2 key models for text generation

35. The key problem to use statistical
language models for IR is..
• How to estimate accurate language model
for a document p(wi|d)?
• How to smooth document language model?

36. • Insight
– Discount probabilities of words present in the document
– Re-distribute “taken-away” probability mass across all other
words in the vocabulary
• Laplacian smoothing (additive smoothing)add one unit for
each word count and renormalize
( , ) 1
( | )
| | | |
c w d
p w d
d V



Laplacianfactor
Vocabularysize
w frequency in d
Document length (total # of words)
Smoothing methods

37. P(w)
Word w
MLE estimate
wordsallofcount
wofcount
ML wp )(
Smoothed LM
Visual representation of the
smoothing process and results

38. • Insight
– Should we consider all words as equal?
– Nope.
• Let us use a language model built for the
entire collection to do a better smoothing.
Discounted MLE estimate
Collection language model
( | )
( | )
( | )
DML
d
p w d if w is seen in d
p w d
p w REF otherwise

 

Idea development: smoothing using
the entire collection (Jelinek-Mercer)

39. Idea development: smoothing with the
a priori word distribution (Dirichlet)
• Formally, the Dirichlet distribution has the form
• The nice part of the Dirichlet distribution is in its
connection to Multinomial (conjugate prior):
• Following Bayesian
inference, we have
, where
.

40. Query Type Jelinek- M ercer Dirichlet Abs. Discount ing
Title 0.228 0 .2 56 0.237
Long 0 .2 78 0.276 0.260
0
0.05
0.1
0.15
0.2
0.25
0.3
JM DIR AD
precision
Method
Relative performance of JM, Dir. and AD
TitleQuery
LongQuery
Comparison of language models with
various smoothing functions for IR

41. ( | )
( | )
( | )
DML
d
p w d if w is seen in d
p w d
p w REF otherwise

 

Discounted MLE estimate
ULM for collection
Ranking principle with
smoothing in a general
form
General smoothing formula
 
 
 

 
 
 





0),(,
0),(,0),(,
0),(, 0),(,
)|(log),(log||
)|(
)|(
log),(
)|(log),()|(log),()|(log),(
)|(log),()|(log),(
)|(log),()|(log
dwcVw Vw
d
d
DML
dwcVw
d
dwcVw Vw
dDML
dwcVw dwcVw
dDML
Vw
REFwpqwcq
REFwp
dwp
qwc
REFwpqwcREFwpqwcdwpqwc
REFwpqwcdwpqwc
dwpqwcdqp




Why smoothing is so important while
using language models for information
retrieval?

42. , ( , ) 0
( , ) 0
( | )
log ( | ) ( , )log | | log ( , ) ( | )
( | )
DML
d
w V c w d w Vd
c w q
p w d
p q d c w q q c w q p w REF
p w REF

  

   
Not important for
ranking (relative)
IDF-discounting
TF weight
Document length normalization
(longer documents are discounted less)
• Collection smoothing p(w|C) is similar to TFIDF + length
normalization. Therefore, smoothing is exactly a realization of
classical heuristics used for IR.
• SLM-IR with the simple heuristics can be computed as
efficiently as classical retrieval models (VSM).
Summationover
words from the query
Comparison with classical ranking heuristics

43. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

44. Advanced ranking models based on
statistical language models
• Language models taking into account sentence
structure and interactions between terms (n-gram, ..)
• Cluster smoothing (cosine, LDA, PLSI)
• Translation model (semantic smoothing, cross-
language smoothing)
• Full Bayesian inference models
• Query noise mixture models (detects informative and
uninformative terms in the query)

45. Advanced ranking models based on
statistical language models
• Language models taking into account sentence
structure and interactions between terms (n-gram, ..)
• Cluster smoothing (cosine, LDA, PLSI)
• Translation model (semantic smoothing, cross-
language smoothing)
• Full Bayesian inference models
• Query noise mixture models (detects informative and
uninformative terms in the query)

46. Language models with long range
dependencies
• Take into account interactions between consecutive words in a
document:
• Take into account structure of the query and a document:
• This models, being interesting from theoretical point of view,
don’t lead to significant improvements in ranking quality:
– Requires a lot of parameter tuning on large collection;
– Queries are short => complex interactions of words in a
phrase aren’t that important. Topicality is captured by ULM.

47. Cluster smoothing (1)
• Insight
– Cluster documents and smooth document
language models using language models
estimated for the corresponding cluster.
• According to experiments, this approach doesn’t
leads to serious improvements in quality.
• Reason: hard clustering and extensive parameter
tuning discount important from the cluster more.

48. • Insight
– Document collection has k topics.
– Each cluster is a soft distribution over topics.
• According to experiments, this approach has much
better performance and smoothing works.
• However, this approach hasn’t been used for large
scale collections due to challenges with LDA.
Cluster smoothing – Dirichlet (2)

49. • What to do if a document is on the verge of a
few clusters?
• Do smoothing using the nearest neighbors
Document-centered smoothing (3)

50. • Insight
– All considered models do search using the words from
the query. Do we miss some relevant documents because
of that? Yes.
• Translation model takes into account complex semantic
dependencies between words in a query and documents
• Allows to increase the search quality(recall).
• Challenges with model training and query execution.
1
( | , ) ( | ) ( | )
j
m
t i j j
w Vi
p Q D R p q w p w D

 
Translation model simple LM
Translation model for ranking

51. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

52. • Motivation
– Models based on query-document similarity and
probabilistic document generation models allow to easily
incorporate user relevance feedback for re-ranking.
– Models based on query likelihood (statistical language
models) doesn’t allow to take into account this
information.
• Insight
– Similarly to the Vector Space Model we will represent a
query and a document in the same space (now
probabilistic space) and define a measure of query-
document similarity to enable relevance feedback.
Ranking approach based on probabilistic
distance of statistical language models

53. Relevance feedback in the Vector Space Model
Original query
+
qq
+ +
++
+ +
+
+
++
+
+
+
+
+
-
--
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
+ + +
Irrelevant
documents
New
query
Relevant documents

54. ( 1| , ) ( | , 1)O R Q D P Q D R  
( | , 1)
( 1| , )
( | , 0)
P D Q R
O R Q D
P D Q R

 

Document generation:
Query generation
(language model):
Relevant docs
Irrelevant docs
“Relevant” queries
model
P(D|Q,R=1)
P(D|Q,R=0)
P(Q|D,R=1)
(q1,d1,1)
(q1,d2,1)
(q1,d3,1)
(q1,d4,0)
(q1,d5,0)
(q3,d1,1)
(q4,d1,1)
(q5,d1,1)
(q6,d2,1)
(q6,d3,0)
Direct query:
- P(Q|D,R=1) language model achieves
the highest quality.
Relevance feedback:
- P(D|Q,R=1) useful for the same query
and new documents
- P(Q|D,R=1) useful for new queries
and the same document
Relevance feedback in the models based on
probabilistic ranking principle

55. • Building blocks:
– Representation – statistical language model;
– Similarity function – KL-divergence.
Not important
for ranking
Ranking approach based on probabilistic
distance of statistical language models

56. • MLE estimate of the query language model:
• The formula for documents ranking based on KL-
divergence has the form:
Connections with the basic model based on
query likelihood (simple ULM ranking)

57. Query Q
D
)||( DQD 
Document D
Search
Results
Relevance feedback
F={d1, d2 , …, dn}
FQQ   )1('
Feedbackseparationmodel
Q
F
Feedbackmodel
Incorporating relevance feedback in
this model is very natural
Feedbackloop

58. Talk outline
• Background
– Overview of classical ranking models
– Intro to statistical language models
• Basic language modeling for IR
• Advanced ranking approaches based on
statistical language models
• Ranking approach based on probabilistic
distance of statistical language models
• Conclusions

59. • Advantages:
– Theoretically elegant model (simple parameter tuning, clear
probabilistic assumptions and framework, matches and
generalizes existing approaches).
– Extensible for special problems/domains (themes, opinion
search,..).
– A lot of research in related communities (NLP, MT,..).
– Achieves state-of-the-art ranking accuracy and comparable
with fine-tuned classical heuristic models (Okapi BM25)
– Allows to incorporate relevance feedback
• Disadvantages:
– Requires estimation of a generative model (difficult for no ULMs).
– Computationally more expensive to achieve the same ranking
quality of simple heuristic models.
Comparison of classical ranking models and
models based on query likelihood (SLM)

60. • Theoretical framework for known ranking heuristics
• Empirically models from this algorithmic family achieve
state-of-the-art quality:
– Basic SLM with Dirichlet smoothing
– Basic SLM with domain-dependent document relevance
modeling (URL, PageRank,..).
– Translation model can incorporate semantic connections
between words from the same and different languages.
– Model based on KL-divergence allows to incorporate relevance
feedback within a probabilistic framework.
– Advanced probabilistic models (mixtures, cluster smoothing)
demonstrate model extensibility.
• Fully automated and explained model estimation
Statistical language models (summary)

61. Many thanks to major contributors and
experts on statistical language models!

62. Thank you!