The document presents a hypothesis test involving the weekly production of the model 6la steel by Abul Khayer Steel Company. It details the calculation of population and sample means, standard deviations, and the statistical analysis performed to determine if the mean production differs from 180 at a 0.01 significance level. The conclusion indicates that the null hypothesis cannot be rejected, validating the claim that the mean production remains 180.

1. Presentation On
REAL LIFE HYPOTHESIS TEST
Presented by:
Organized By:
Mohammad Khaled Afzal,
Professor,
Department Of Management,
University Of Chittagong.
Ashik Amin Prem
Department of Management,
University of Chittagong.

2. Real Life Example Of Hypothesis
10 weeks production Of AKS Company (In MT):
1st
Week
2nd
Week
3rd
Week
4th
Week
5th
Week
6th
Week
7th
Week
8th
Week
9th
Week
10th
Week
203.2 365.7 102.8 150.1 95.7 302.8 182.2 73.8 90.1 233.6

3. Real Life Example Of Hypothesis
To prove the hypothesis test,
We need to show population mean, sample mean and
population standard deviation…

4. Real Life Example Of Hypothesis
Population Mean & Standard Deviation :
Weak Production (x) (x-μ) (x-μ)²
1 203.2 23.2 538.24
2 365.7 185.7 34484
3 102.8 -77.2 5959.8
4 150.1 -29.9 894.01
5 95.7 -84.3 7106.49
6 302.8 122.8 15079.8
7 182.2 2.2 4.84
8 73.8 -106.2 11278.4
9 90.1 -89.9 8082.01
10 233.6 53.6 2872.96
Total (∑x) 1800
Mean (μ) 180 ∑(x-μ)²=86300.55

5. Real Life Example Of Hypothesis
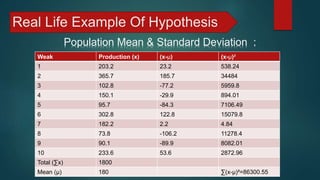
σ = √[∑(x-μ)²/N]
= √(86300.55/10)
=92.89
[Where N=10]
Standard Deviation (Population):

6. Real Life Example Of Hypothesis
Sample mean (On 5 Weeks) :
Weak Production (x)
1 203.2
2 365.7
3 102.8
4 150.1
5 95.7
Sample Mean, (x̄ ) 183.5

7. Real Life Example Of Hypothesis
Question:
Abul Khayer Steel Company, Chittagong manufactures an assembles
steels equipment at several plant in Chittagong. The weekly production of
the model 6LA steel follows a normal probability distribution with mean of
180 and a standard deviation of 92.89. Recently, because of market
expansion, new production methods have been introduced and new
employees hired. The executive of manufacturing would like to
investigate whether there has been a change in the weekly production of
the model 6LA steel. Is the mean number of steels produced different
from 180 at the 0.01 significance level?
[The mean number of steels produced is 183.5 (5 weaks)]

8. Real Life Example Of Hypothesis
Solution:
Step 1: Make Assumptions and Meet Test Requirements:
One sample test and two tail hypothesis test.
Population Mean, μ = 180
Population Standard Deviation, σ = 92.89
Sample Size, n = 5
Sample Mean, (x̄ )= 183.50
Level of Significance, α = 0.01

9. Real Life Example Of Hypothesis
Solution:
Step 2: State the Null Hypothesis and Alternative Hypothesis:
Null Hypothesis, Ho: μ = 180
Alternative Hypothesis, H1: μ ≠ 180

10. Real Life Example Of Hypothesis
Solution:
Step 3: Select Sampling Distribution and Establish the Critical Region:
The test statistic for a mean, when σ known is z test.
And it is a two tailed test.
σ ✓ σ ✗
n>30 z distribution, z table z distribution, z table
n<30 z distribution, z table t distribution, t table

11. Real Life Example Of Hypothesis
Solution:
Step 3: Select Sampling Distribution and Establish the Critical Region:
0.005 0.005
0.4950 0.4950
0.5000 0.5000
μ = 180-2.58 +2.58
Critical Value Critical Value
α = 0.01
Two Tail Test
ZCritical Value ±2.58

12. Real Life Example Of Hypothesis
Solution:
Step 4: Use Formula to Compute the Test Statistic:
= (x̄- μ)/ ^σx̅
=(183.5-180 )/(92.89/√5)
=3.5/41.54
=0.084
ZCalculate Population Mean, μ = 180
Sample Mean, (x̄ )= 183.50
Standard Error of the Mean,
^σx̅
= σ/√n = 41.54.

13. Real Life Example Of Hypothesis
Solution:
Step 5: Make a Decision and Interpret Results:
Absolute Zcal = 0.084 < Absolute Zcrt = 2.58.
The Null Hypothesis can not be rejected.
Decision:
The claim of the mean number of steels 180 is valid.

14. THE END