This document describes a project on game theory completed by 6 students. It includes an index listing the various topics covered in the project such as the history of game theory, definitions of key terms, assumptions of games, and methods for finding solutions to games including pure strategies, dominance rules, and mixed strategies. The project received certification that it satisfactorily addressed the required topics on game theory.

1. SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
Theory of Game
Project work

2.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
2
CERTIFICATE
This is to certify that project work for the subject of
“Theory of Game” by
A Subjected to the project of Mathematics,
satisfactorily completed their teamwork in course of B.Sc.
(sem-5th
& 6th
) during the year 2020-2021.
Date: Project Guide
Examiner’s Signature Head of Department
Name
1. Lakum Chiragbhai J.
2. Chavda Hiralal H.
3. Hirani Brijesh V.
4. Degamadiya Bhavikbhai T.
5. Parmar Dipen K.
6. Thadoda Akshaykumar N.
Enrollment No.
3101184329
3101184867
3101184895
3101184264
3101184376
3101184433
Roll No.
138
125
132
128
145
151

3.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
3
ACKNOWLEDGMENT
The successful completion of this project rests on
the shoulder of many persons who were helpful to us
directly or indirectly. We wish to take this opportunity to
express our appreciation to all of them, without whose
help the completion of this project would have been
difficult.
We are thankful to Prof. N.T.Chotaliya (H.O.D. of
Maths Department) & Dr. Amit kumar Mishra (Principle)
for his keen effort to Improve our education system
and provide opportunity for this innovative project. We
are thankful to Asst. Prof. M.P. Shekhavat and Asst .
prof. Jaydeep dodiya for his support,guidance and advice.
We are thankful to all our friend and well-
wishers, for their Continuous support and valuable
tips. We are thankful to all those Who are directly or
indirectly involved in the completion of this Project.
Last but not the least we are obliged beyond
words to our Loving parents without their help,
support and everlasting Inspiration we would have
been unable to achieve this feat.

4.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
4
INDEX
1. HISTORY............................................................ 5
2. DEFINITION OF GAME THEORY............................. 5
3. BASIC TERM USED IN GAME THOERY.................... 6
4. ASSUMPTIONS OF THE GAME............................... 8
5. FLOW CHART OF GAME THEORY ........................... 9
6. RULES FOR GAME THEORY..................................10
7. PURE STRATEGIES (MINIMAX AND MAXIMIN
PRINCIPLE) .............................................................10
8. RULE TO FINDOUT SADDLE POINT.......................11
9. DOMINANCE RULES ...........................................13
10. MIXED STRATEGY (GAME WITHOUT SADDLE
POINT) ...................................................................16
10.1 ALGEBRIC METHOD......................................16
10.2 ARITHMETIC METHOD ..................................21
10.3 MATRIX METHOD .........................................25
10.4 GRAPHICAL METHOD....................................27
10.5 LINEAR PROGRAMMING METHOD ..................35

5.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
5
1. HISTORY
2. DEFINITION OF GAME THEORY
In business and economics literature, the term
'game' refers to a situation of conflict and competition
in which two or more competitor(or participant) are
involved in the decision making process in
anticipation of certain outcome over a period of time.
 In Game theory came in to
existence in 20th
Century.
 In 1944 John Von Neumann and
Oscar Morgenstern published a
book Theory of game and
Economic Behavior which they
discussed how businesses of all
types may use this technique to
determine the best strategies
given a competitive business
environment John Von Neumann

6.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
6
3. BASIC TERM USED IN GAME THOERY
3.1 PLAYER
The competitor is referred to as player A player may
be individual, a group of individual, or an organization.
3.2 TWO-PERSON GAME/ N-PERSON GAME
 If a game involves only two players (competitors),
then it is called a two-person game.
 If numbers of player are more than two, then game
is referred to as n-person game.
3.3 ZERO SUM GAME/NON-ZERO SUM GAME
In a game, if sum of the gain to one player is
exactly equal to the sum of losses to another player, so
that the sum of the gains and losses equals to zero, then
the game is said to be a zero-sum game. Otherwise it is
said to be non zero-sum game.
3.4 STRATEGY
The strategy for a player is the list of all possible
actions (moves or courses of action) that he will take for
every payoff (outcome) that might arise.
3.4.1PURE STRATEGY
 A player always chooses the same strategy-same
row or column.
3.4.2MIXED STRATEGY
 A player chooses the strategy with some fix
probabilities.
 A player changes the choice of row or column with
different plays or turns.

7.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
7
3.4.3OPTIMAL STRATEGY
The particular strategy by which a player optimizes
his gains or losses without knowing the competitors
strategies is called optimal strategy.
3.5 PAYOFF MATRIX
The payoff (a quantitative measure of satisfaction
that a player gets at the end of the play) in terms of
gains and losses, when player select their particular
strategies, can be represented in the form of a matrix,
called the payoff matrix.
In this pay-off matrix, positive pay-off is the gain to
maximizing player (X) and loss to minimizing player (Y).
E.g., if X chooses strategy X2 and Y chooses strategy Y1,
then X’s gain is 32 and Y's loss is 32.
24 36 8
32 20 16
PLAYER
X
PLAYER Y
Y1 Y2 Y3
X1
X2

8.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
8
4. ASSUMPTIONS OF THE GAME
1.There are finite numbers of competitors.
2. There is conflict of interests between them.
3.Each player has available with him finite number
of possible strategies (courses of action). The list
may not be the same for each player.
4.One player attempts to maximize gains and the
other attempts to minimize losses.
5.Players know all possible available choices but do
not know which one is going to be chosen.
6.Players simultaneously select their respective
courses of action.
7.The payoff is fixed and determined in advance.
8.Players have to make individual decisions without
direct communication.

9.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
9
5. FLOW CHART OF GAME THEORY

10.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
10
6. RULES FOR GAME THEORY
RULE 1: Look for pure Strategy (Saddle point)
RULE 2: Reduce game by Dominance
If no pure strategies exist, the next step is to eliminate
certain strategies (row/column) by law of Dominance.
RULE 3: Solve for mixed Strategy
A mixed strategy game can be solved by different
solution method, such as
1. Algebraic Method
2. Arithmetic Method
3. Matrix Method
4. Graphical method
5. Linear Programming Method
7. PURE STRATEGIES (MINIMAX AND MAXIMIN PRINCIPLE)
(1) Maximin principle:
Maximize the player’s minimum gains. That means
select the strategy that gives the maximum gains among
the row minimum value.
(2) Minimax Principle:
Minimize the player’s maximum gains. That means,
select the strategy that gives the minimum loss among
the column maximum values.

11.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
11
(3) Saddle Point:
If the maximin value equals the minimax value, the
game is said to have a saddle (equilibrium) point and the
corresponding strategies are called "Optimal Strategies".
(4) Value of game:
This is the expected payoff at the end of the game,
when each player uses his optimal strategy.
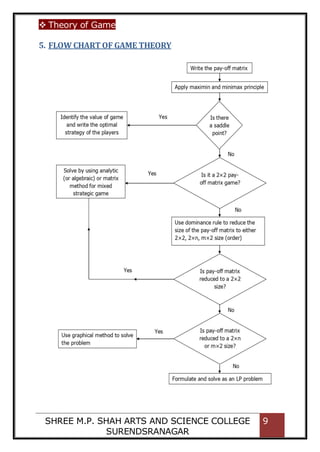
8. RULE TO FINDOUT SADDLE POINT
 Select the minimum (lowest) element in each row of
the payoff matrix and write them under ‘Row
Minimum’ heading. Then, select the largest element
among these element and enclose it in a
rectangle [ ].
 Select the maximum (largest) element in each
column of the pay off matrix and write them under
'Column Maximum' heading. Then, select the lowest
element among these elements and enclose it in a
circle ( ).
 Find out the element(s) that is same in the circle as
the well as rectangle and mark the position of such
element(s) in the matrix. This element represents
the value of the game and is called the Saddle (or
equilibrium) point.
Example: Find Solution of game theory problem
using saddle point

12.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
12
Player APlayer B
B1 B2
A1 4 6
A2 3 5
Solution:
We apply the maximin (minimax) principle to analyze the
game,
Select minimum from the maximum of columns
Column MiniMax = (4)
Select maximum from the minimum of rows
Row MaxiMin = [4]
Here, Column MiniMax = Row MaxiMin = 4
∴ This game has a saddle point and value of the game is
4.
The optimal strategies for both players are,
The player A will always adopt strategy A1.
The player B will always adopt strategy B1.
Player APlayer B
B1 B2
Row
Minimum
A1 [(4)] 6 [4] Maximin
A2 3 5 3
Column
Maximum
(4)
Minimax
6

13.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
13
Why Dominance Rules used?
 To reduce size of payoff matrix in game theory
9. DOMINANCE RULES
Step-1: If all the elements of Column-i are greater than
or equal to the corresponding elements of any other
Column-j, then the Column-i is dominated by the
Column-j and it is removed from the matrix.
eg. If all values of Column-2 ≥ Column-4, then remove
Column-2
Step-2: If all the elements of a Row-i are less than or
equal to the corresponding elements of any other Row-j,
then the Row-i is dominated by the Row-j and it is
removed from the matrix.
eg. If all values of Row-3 ≤ Row-4, then remove Row-3
Step-3: If strategy k is dominated by average of any two
strategy i and j than delete column or row strategy k
Example: Given problem Reduced 2×2 matrix using
dominance method
Player APlayer B
B1 B2 B3 B4
A1 3 5 4 2
A2 5 6 2 4
A3 2 1 4 0
A4 3 3 5 2
Solution:
Dominance rule to reduce the size of the payoff matrix

14.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
14
Using dominance property
Player APlayer B
B1 B2 B3 B4
A1 3 5 4 2
A2 5 6 2 4
A3 2 1 4 0
A4 3 3 5 2
row-3 ≤ row-4, so remove row-3
(A3≤A4: 2≤3,1≤3,4≤5,0≤2)
Player APlayer B
B1 B2 B3 B4
A1 3 5 4 2
A2 5 6 2 4
A4 3 3 5 2
column-2 ≥ column-4, so remove column-2
(B2≥B4:5≥2,6≥4,3≥2)
Player APlayer B
B1 B3 B4
A1 3 4 2
A2 5 2 4
A4 3 5 2
column-1 ≥ column-3, so remove column-1.
(B1≥B4:3≥2,5≥4,3≥2)

15.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
15
Player APlayer B
B3 B4
A1 4 2
A2 2 4
A4 5 2
row-1 ≤ row-3, so remove row-1, (A1≤A4: 4≤5,2≤2)
Player APlayer B
B3 B4
A2 2 4
A4 5 2
Example: Find Solution of game theory problem
using dominance method
Solution:
Dominance rule to reduce the size of the payoff matrix
Using dominance property
row-3 ≤ row-2, so remove row-3
(A3≤A2:5≤5,-20≤-10,-20≤-10)
Player APlayer B
B1 B2 B3
A1 -5 10 20
A2 5 -10 -10
A3 5 -20 -20
Player APlayer B
B1 B2 B3
A1 -5 10 20
A2 5 -10 -10
A3 5 -20 -20

16.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
16
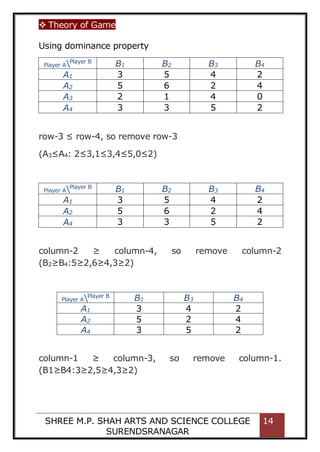
column-3 ≥ column-2, so remove column-3.
(B3≥B2:20≥10,-10≥-10)
Player APlayer B
B1 B2
Row
Minimum
A1 -5 10 [-5] Maximin
A2 5 -10 -10
Column
Maximum
(5)
Minimax
10
Note: The maximin value is not equal to minimax value;
hence there is no saddle point. For this type of game
situation, it is possible to obtain a solution by applying
the concept of mixed strategies.
10. MIXED STRATEGY (GAME WITHOUT SADDLE POINT)
In certain case, there is no pure strategy solution for
a game. i.e. No Saddle Point exists.
10.1 ALGEBRIC METHOD
This method is used to determine the probability of
using different strategies by players A and B. This method
becomes quite lengthy when a number of strategies for
both the players are more than two.
Player APlayer B
B1 B2 B3
A1 -5 10 20
A2 5 -10 -10

17.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
17
Consider a game where the payoff matrix is: [aij]m×n.
Let (p1,p2,…,Pm) and (q1,q2,…,qn) be the probabilities with
which players A and B select their strategies
(A1,A2,...,Am) and (B1 ,B2 ,…, Bn ),respectively. If v is the
value of game, then the expected gain to player A, when
player B selects strategies B1, B2,…,Bn, one by one, is given
left –hand side of the following simultaneous equations,
respectively. Since player A is the gainer player and
expects at least V, therefore, we must have
Player APlayer B
B1 B2 …. Bn
A1 a11 a12 …. a1n
A2 a21 a22 …. a2n
:
:
An am1 am2 … amn
a11 p1 + a21 p2 +…+ am1 pm ≥V
a12 p1 + a21 p2 +…+ am2 pm ≥V
: : :
: : :
a1n p1 + a2n p2 +…+ amn pm ≥V
where, p1 + p2 +. . .+ pm=1 and pi ≥ 0 for all i
Similarly, the expected loss to player B, when player A
selects strategies A1, A2,..., Am, One by one, can also be
determined. Since player B is the loser player, therefore,
he must have:
probability
p1
p2
:
:
pm
Probability q1 q2 … qn

18.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
18
a11 q1+ a12 q2 +…+ a1n qn ≤V
a21 q1 + a22 q2 +…+ a2n qn≤V
: : :
: : :
am1 q1 + am2 q2 +…+ amn qn ≤V
Where, q1 + q2 + ... + qn = 1 and qj≥ 0 for all j
To get the values of pi's and qj's, the above
inequalities are considered as equations and are then
solved for given unknowns. However, if the system of
equations, so obtained, is inconsistent, then at least One
of the inequalities must hold as a strict inequality. The
solution can now be obtained only by applying the trial
and error method.
Example: Find Solution of game theory problem
using algebraic method
Player APlayer B
B1 B2
A1 5 2
A2 3 4
Solution:
 Saddle point testing
Player APlayer B
B1 B2
A1 5 2
A2 3 4
 We apply the maximin (minimax) principle to analyze
the game.

19.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
19
Select minimum from the maximum of columns
Column MiniMax = (4)
Select maximum from the minimum of rows
Row MaxiMin = [3]
Here, Column MiniMax ≠ Row MaxiMin
∴ This game has no saddle point.
 Solution using algebraic method
Let, p1= probability of selecting the strategy A1,
p2= probability of selecting the strategy A2,
q1= probability of selecting the strategy B1,
Player APlayer B
B1 B2
Row
Minimum
A1 5 2 2
A2 [3] (4) [3] Maximin
Column
Maximum
5 (4)
Minimax
Player APlayer B
B1 B2
A1 5 2
A2 3 4
q1 q2
p1
p2

20.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
20
q2= probability of selecting the strategy B2
And V be the value of game,
5 p1+3 p2=v………………………………(1)
2 p1+4 p2=v………………………………(2)
p1+ p2=1……………………………… (3)
After solving above three equation,
p1=
1
4
, p2=
3
4
V=
7
2
Therefore optimum strategy for player A is(1/4 ,3/4).
Player A should play strategy A1 25% time and A2 75%
time in order to maximize is expected game by 7/2 units.
In the same way for player B
5 q1+2 q2=v ……………………………… (1)
3 q1+4 q2=v……………………………… (2)
q1+ q2=1……………………………… (3)
After solving above equation,
q1=
1
2
, q2=
1
2
V=
7
2

21.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
21
Therefore optimum strategies for player B is (1/2, 1/2)
player B should play strategy B1 50% time and B2 50%
time in order to minimize is expected game by 7/2 unit.
10.2 ARITHMETIC METHOD
The arithmetic method (also known as short cut
method) provides an easy method for finding optimal
strategies for each player in a payoff matrix of size 2*2,
without saddle point.
The steps of this method are as follows:
Step-1: Find the differences between the two values
in the first row and put it against the second row of
the matrix. Neglecting the negative Sign (if any).
Step-2: Find the differences between the two values
in the second row and put it against the first row of
the matrix. Neglecting the negative sign (if any).
Step-3: Repeat step 1 and step 2 for two columns
also.
The values obtained by ‘swapping the difference’
represent the optimal relative frequency of play for both
players’ strategies. These may be converted to
probabilities by dividing each of them by their sum.
Example: Find Solution of game theory problem
using arithmetic method
Player APlayer B
B1 B2
A1 2 -1
A2 -1 0

22.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
22
Solution:
 Saddle point testing
Player APlayer B
B1 B2
A1 2 -1
A2 -1 0
 We apply the maximin (minimax) principle to analyze
the game.
Select minimum from the maximum of columns
Column MiniMax = (0)
Select maximum from the minimum of rows
Row MaxiMin = [-1]
Here, Column MiniMax ≠ Row MaxiMin
∴ this game has no saddle point.
Player APlayer B
B1 B2
Row
Minimum
A1 2 [-1] [-1] Maximin
A2 -1 (0) -1
Column
Maximum
2 (0)
Minimax

23.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
23
 using arithmetic method to get optimal mixed
strategies for both the players,
Player APlayer B
B1
B2
A1 2 -1
A2
-1 0
1.Find absolute difference between the two values
in the first row and put it against second row of
the matrix
│2-(-1) │=3
2.Find absolute difference between the two values
in the second row and put it against first row of
the matrix
│-1-0│=1
∴ p1=
1
1+3
=
1
4
∴ p2=
3
3+1
=
3
4
Hence, Player A should adopt A1 and A2 with 25% of
time and 75% of time respectively.
│-1-0│=1 │2-(-1)│=3
∴ q1=
1
1+3
=
1
4
∴ q2=
3
3+1
=
3
4
│-1-0│=1 ∴ p1=
1
1+3
=
1
4
│2-(-1) │=3 ∴ p2=
3
3+1
=
3
4

24.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
24
3.Find absolute difference between the two values
in the first column and put it against second
column of the matrix
│2-(-1) │=3
4.Find absolute difference between the two values
in the second column and put it against first
column of the matrix
│-1-0│=1
∴ q1=
1
1+3
=
1
4
∴ q2=
3
3+1
=
3
4
Hence, Player B should adopt B1 and B2 with 25% of
time and 75% of time respectively.
Expected gain of Player A
(1) 2×
1
4
+ (-1)×
3
4
= -
1
4
, Player B adopt B1
(2) (-1)×
1
4
+ 0×
3
4
= -
1
4
, Player B adopt B2
Expected loss of Player B
(1) 2×
1
4
+ (-1)×
3
4
= -
1
4
, Player A adopt A1
(2) (-1)×
1
4
+ 0×
3
4
= -
1
4
, Player A adopt A2

25.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
25
10.3 MATRIX METHOD
If the game matrix is in the form of a square
matrix, then the optimal strategy mix as well as value of
the game may be obtained by the matrix method.
The solution of a two-person zero-sum game with
mixed strategies with a square payoff matrix may be
obtained by using the following formula:
Player A's optimal strategy =
[1 1]𝑃𝑎𝑑𝑗
[1 1] 𝑃𝑎𝑑𝑗[
1
1
]
=[𝑝1 𝑝2]
Player B's optimal strategy =
[1 1]𝑃𝑐𝑜𝑓
[1 1] 𝑃𝑎𝑑𝑗[
1
1
]
=[𝑞1 𝑞2]
Value of the game = (Player A's optimal strategies) x
(Payoff matrix pij ) × (Player B's optimal strategies)
V=[𝑝1 𝑝2] × 𝑝 × [
𝑞1
𝑞2
]
Where padj = adjoint matrix, Pcof= cofactor matrix.
Player A's optimal strategies are in the form of a row
vector and B's optimal strategies are in the form of a
column vector.
This method can be used to find a solution of a
game with size of more than 2x2. However, in rare
cases, the solution violates the non-negative
condition of probabilities, i.e. pi ≥ 0, qi ≥ 0, although
the requirement p1 + p2 + …+ pm = 1 or q1 + q2 +…+
qn= 1 is met.

26.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
26
Example: Find Solution of game theory problem
using matrix method
Player APlayer B
B1 B2
A1 1 7
A2 6 2
Solution:
For reduced matrix, calculated PAdj and PCof
PAdj =[
2 −7
−6 1
]
PCof =[
2 −6
−7 1
]
Player A's optimal strategy =
[1 1]𝑃𝑎𝑑𝑗
[1 1]× 𝑃𝑎𝑑𝑗×[
1
1
]
=
[1 1][
2 −7
−6 1
]
[1 1][
2 −7
−6 1
][
1
1
]
=
[−4 −6]
−10
=[
2
5
3
5
]
P1=
2
5
and P2=
3
5
,
Where p1 and p2 represent the probabilities of player A’s,
using his strategies A1 and A2 respectively.
Player B's optimal strategy =
[1 1]𝑃𝑐𝑜𝑓
[1 1] 𝑃𝑎𝑑𝑗[
1
1
]

27.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
27
=
[1 1][
2 −6
−7 1
]
[1 1][
2 −7
−6 1
][
1
1
]
=
[−5 −5]
−10
=[
1
2
1
2
]
q1=
1
2
and q2=
1
2
,
Where q1 and q2 represent the probabilities of player B’s,
using his strategies B1 and B2 respectively.
Value of the game = (Player A's optimal strategies) x
(Payoff matrix pij ) × (Player B's optimal strategies)
V=[𝑝1 𝑝2] × 𝑝 × [
𝑞1
𝑞2
]
V=[
2
5
3
5
] [
1 7
6 2
] [
1
2
1
2
]=4
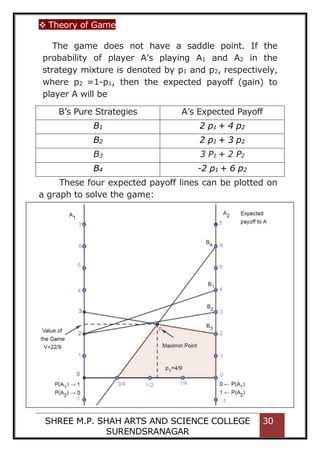
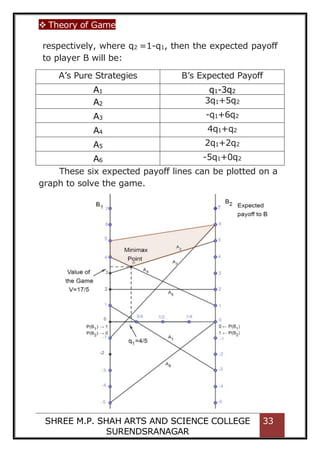
10.4 GRAPHICAL METHOD
The graphical method is useful for the game
where the payoff matrix is of the size 2 x n or m x 2,
i.e. the game with mixed strategies that has only two
undominated pure strategies for one of the players in
the two person zero-sum game.

28.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
28
Optimal strategies for both the players assign
non-zero probabilities to the same number of pure
strategies. Therefore, if one player has only two
strategies, the other will also use the same number of
strategies. Hence, this method is useful in finding
out which of the two strategies can be used.
Consider the following 2 x n payoff matrix of a
game, without saddle point.
Player A has two strategies A1 and A2 with
probability of their selection p1 and p2, respectively,
such that p1 + p2 = 1 and p1, p2 ≥ 0. Now for each of the
pure strategies available to player B, the expected pay
off for player A would be as follows:
B’s Pure Strategies A’s Expected Payoff
B1 a11 p1 + a21 p2
B2 a12 p1 + a21 p2
: :
Bn a1n p1 + a2n p2
According to the maximin criterion for mixed
strategy games, player A should select the value of

29.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
29
probability p1 and p2 so as to maximize his minimum
expected payoffs. This may be done by plotting the
straight lines representing player A's expected payoff
values.
The highest point on the lower boundary of these
lines will give the maximum expected payoff among the
minimum expected payoffs and the optimum value of
probability p1 and p2.
Now the two strategies of player B corresponding to
those lines which pass through the maximum point can
be determined. This helps in reducing the size of the
game to (2 x 2), which can be easily solved by any of
the methods discussed earlier.
The(m x 2) games are also treated in the same
way except that the upper boundary of the straight
lines corresponding to B's expected payoff will give the
maximum expected payoff to player B and the lowest
point on this boundary then give the minimum
expected payoff (minimax value) and the optimum
value of probability q1 and q2.
Example: Find Solution of game theory problem
using graphical method
Player APlayer B
B1 B2 B3 B4
A1 2 2 3 -2
A2 4 3 2 6
Solution:

30.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
30
The game does not have a saddle point. If the
probability of player A’s playing A1 and A2 in the
strategy mixture is denoted by p1 and p2, respectively,
where p2 =1-p1, then the expected payoff (gain) to
player A will be
B’s Pure Strategies A’s Expected Payoff
B1 2 p1 + 4 p2
B2 2 p1 + 3 p2
B3 3 P1 + 2 P2
B4 -2 p1 + 6 p2
These four expected payoff lines can be plotted on
a graph to solve the game:
1111111111111111111

31.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
31
Now the original (2×4) game reduces to that of the
game with payoff matrix of size (2×2) as given below:
 Solution using algebraic method
The optimal payoff to player A,
3 p1+2(1-p1) =v……………………………… (1)
-2 p1+6(1-p1) =v……………………………… (2)
p1+ p2=1……………………………… (3)
Now solving above three equation,
p1=
4
9
p2=
5
9
V= 3×
4
9
+ 2×
5
9
=
22
9
Therefore optimum strategy for player A is (4/9, 5/9).
Player A should play strategy A1 44.44% time and A2
55.55% time in order to maximize is expected game by
22/9 units.
The optimal payoff to player B can be found in the same
way,
3 q3-2(1-q3) =v……………………………… (1)
Player APlayer B
B3 B4
A1 3 -2
A2 2 6
q3 q4
P1
P2=1-p1

32.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
32
2 q3+6(1-q3) =v……………………………… (2)
q3+ q4=1……………………………… (3)
After solving above equation,
q1=
8
9
q2=
1
9
V= 3×
8
9
+ 2×
1
9
=
22
9
Therefore optimum strategies for player B is
(0,0,8/9,1/9) player B should play strategy B3 88.88%
time and B4 11.11% time in order to minimize is
expected game by 22/9 unit.
Example: Obtain the optimal strategies for both
person and the value of game for two-person zero
sum game whose payoff matrix is as follows:
Player APlayer B
B1 B2
A1 1 -3
A2 3 5
A3 -1 6
A4 4 1
A5 2 2
A6 -5 0
Solution:
The game does not have a saddle point. If the
probability of player B’s playing strategies B1 and B2 in
the strategy mixture is denoted by q1 and q2,

33.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
33
respectively, where q2 =1-q1, then the expected payoff
to player B will be:
A’s Pure Strategies B’s Expected Payoff
A1 q1-3q2
A2 3q1+5q2
A3 -q1+6q2
A4 4q1+q2
A5 2q1+2q2
A6 -5q1+0q2
These six expected payoff lines can be plotted on a
graph to solve the game.

34.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
34
Now the original (6×2) game reduces to that of the
game with payoff matrix of size (2×2) as given below:
 Solution using algebraic method
The optimal payoff to player A,
3 p2+4(1-p2) =v ………………………………… (1)
5 p2+1(1-p2) =v………………………………… (2)
P2+ p4=1………………………………… (3)
Now solving above three equation,
p1=
3
5
p2=
2
5
V= 3×
3
5
+ 2×
2
5
=
17
5
Therefore optimum strategy for player A is
(0,3/5,0,2/5,0,0). Player A should play strategy A2 60%
time and A4 40% time in order to maximize is expected
game by 17/5 units.
The optimal payoff to player B can be found in the same
way,
3 q1+5(1-q1) =v…………………………………(1)
Player APlayer B
B1 B2
A2 3 5
A4 4 1
q1 q2
P2
P4=1-p2

35.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
35
4 q1+1(1-q1) =v………………………………… (2)
q1+ q2=1………………………………… (3)
After solving above equation,
q1=
4
5
q2=
1
5
V= 3×
4
5
+ 2×
1
5
=
17
5
Therefore optimum strategies for player B is (4/5,1/5)
player B should play strategy B1 80% time and B2 20%
time in order to minimize is expected game by 17/5 unit.
10.5 LINEAR PROGRAMMING METHOD
The two-person zero-sum games can also be solved
by linear programming. The major advantage of using
linear programming technique is that it helps to solve the
mixed-strategy games of larger dimension payoff matrix.
To illustrate the transformation of a game problem
to a linear programming problem, consider a payoff
matrix of size m x n. Let aij be the element in the ith
row
and jth
column of game payoff matrix, and letting pi be
the probabilities of m strategies (i = 1, 2,..., m) for
player A. Then, the expected gains for player A, for
each of player B's strategies will be:
V= ∑ 𝑝𝑖𝑎𝑖𝑗
𝑚
𝑖=1
j=1, 2,…,n

36.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
36
The aim of player A is to select a set of strategies
with probability pi (i = 1, 2,..., m) on any play of game
such that he can maximize his minimum expected
gains.
Now to obtain values of probability pi, the value the
game to player A for all strategies by player B must be
at least equal to V. Thus to maximize the minimum
expected gains, it is necessary that:
a11 p1 + a21 p2 +…+ am1 pm ≥V
a12 p1 + a21 p2 +…+ am2 pm ≥V
: : :
: : :
a1n p1 + a2n p2 +…+ amn pm ≥V
Where, p1 + p2 +…+pm=1 and pi ≥ 0 for all i
Dividing both sides of the m inequalities and
equation by V the division is valid as long as V<0, the
direction of inequality constrains must be reversed. But if
v=0, the division would be meaningless. In this case a
constant can be added to all entries of the matrix, ensuring
that the value of the game (V) for the revised matrix
becomes more than zero. After optimal solution is
obtained, the true value of the game is obtained by
subtracting the same constant value. Let
𝑝𝑖
𝑉
=xi, (≥0), we
then have
a11
𝑝1
𝑉
+ a21
𝑝2
𝑉
+…+ am1
𝑝𝑚
𝑉
≥1
a12
𝑝1
𝑉
+ a22
𝑝2
𝑉
+…+ am2
𝑝𝑚
𝑉
≥1
: : :
: : :

37.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
37
a1n
𝑝1
𝑉
+ a2n
𝑝2
𝑉
+…+ amn
𝑝𝑚
𝑉
≥1
𝑝1
𝑉
+
𝑝2
𝑉
+...+
𝑝𝑚
𝑉
=1
Since the objective of player A is to maximize the
value of the game, V, which is equivalent to minimizing
1/V, the resulting linear programming problem can be
stated as:
Minimize Zp (=1/V) = x1 + x2 +…+xm
Subject to the constraints
𝑝𝑖
𝑉
≥ 0
a11 x1 + a21 x2 +…+ am1 xm ≥1
a12 x1 + a21 x2 +…+ am2 xm ≥1
: : :
: : :
a1n x1 + a2n x2 +…+ amn xm ≥1
x1 ,x2,…,xm≥0
Where, xi =
𝑝𝑖
𝑉
≥0 ; i=1,2,…,m
Similarly, Player B has similar problem with the
inequalities of the constraints reversed, i.e. minimize the
expected loss. Since minimizing V equivalent to
maximizing 1/V, therefore, the resulting linear
programming problem can be stated as:
Maximize Zq (=1/V) = y1 + y2 +…+yn
Subject to the constraints
a11 y1 + a12 y2 +…+ a1n yn ≤1
a21 y1 + a22 y2 +…+ a2n yn ≤1
: : :

38.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
38
: : :
am1 y1 + am2 y2 +…+ amn yn≤ 1
y1 ,y2,…,ym≥0
Where, yj=
𝑞𝑖
𝑉
≥0 j=1,2,…,n
It may be noted that the LP problem for player B is
the dual of LP problem for player A and vice versa.
Therefore, the solution of the dual problem can be
obtained from the primal simplex table. Since for both
the players Zp = Zq the expected gain to player A in the
game will be exactly equal to expected loss to Player B.
Remark: Linear programming technique requires all
variables to be non-negative and therefore to obtain a
non-negative of value V of the game, the data to the
problem, i.e. aij in the payoff table should all be a non-
negative. If there are some negative elements in the
payoff table, a constant to every element in the payoff
table must be added so as to make the smallest element
zero; the solution to this new game will give of optimal
mixed strategy for the original game. The element the
original game then equals the value of the new game
minus the constant.
Example: Find Solution of game theory problem
using linear programming method
Player APlayer B
B1 B2 B3
A1 1 -1 3
A2 3 5 -3
A3 6 2 2

39.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
39
Solution:
 We apply the maximin (minimax) principle to
analyze the game.
Player APlayer B
B1 B2
B3 Row
Minimum
A1 1 [-1] (3) [-1]
A2 3 5 -3 -3
A3 6 2 2 -2
Column
Maximum
6 5 (3)
Select minimum from the maximum of columns
Column MiniMax = (3)
Select maximum from the minimum of rows
Row MaxiMin = [-1]
Here, Column MiniMax ≠ Row MaxiMin
∴ this game has no saddle point.
Since the maximin value is -1, it is possible that the value
of game (V) may be negative or zero because -1<V<3.
Thus, a constant k is added to all the element of payoff
matrix. Let k=4, then the given payoff matrix becomes:
Player APlayer B
B1 B2 B3
A1 5 3 7
A2 7 9 1
A3 10 6 2
Probability q1 q2 q3
Probability
p1
p2
P3

40.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
40
Let pi(i=1,2,3) and qi(j=1,2,3) be the probabilities of
selecting Ai(i=1,2,3) and Bj(j=1,2,3) by player A and B,
respectively.
The expected gain for player A will be as follows :
5p1 +7p2 + 10p3≥V (if B uses strategy B1)
3p1 +9p2 +6p3≥V (if B uses strategy B2)
7p1 + p2 +2p3≥V (if B uses strategy B3)
Where, p1 + p2 + p3=1 and p1 , p2 , p3≥ 0
Dividing the above constraints by V, we get
5(
𝑝1
𝑉
) +7(
𝑝2
𝑉
) +10(
𝑝3
𝑉
) ≥1
3(
𝑝1
𝑉
)+9(
𝑝2
𝑉
)+6(
𝑝3
𝑉
) ≥1
7(
𝑝1
𝑉
)+ (
𝑝2
𝑉
) +2(
𝑝3
𝑉
) ≥1
𝑝1
𝑉
+
𝑝2
𝑉
+
𝑝3
𝑉
=
1
𝑉
To simplify the problem, we put
𝑝1
𝑉
=x1,
𝑝2
𝑉
=x2,
𝑝3
𝑉
=x3
In order to maximize V, player A can
Minimize ZP( =
1
𝑉
) =x1 + x2 + x3
Subject to constraints,
5x1 +7x2 +10x3 ≥ 1

41.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
41
3x1 +9x2+6x3 ≥ 1
7x1 + x2 +2x3 ≥1
And x1,x2 ,x3 ≥0
Player B's objective is to minimize its expected
losses that can be reduced to by minimizing the value
of the game V. Hence the problem of B can be
expressed as follows:
Maximize Zq(=
1
𝑉
)=y1+y2+y3
Subject to constraints,
5y1+3y2+7y3≤1
7y1+9y2+y3≤1
10y1+6y2+2y3≤1
and y1,y2,y3≥0
Where y1=
𝑞1
𝑉
; y2=
𝑞2
𝑉
; y1=
𝑞3
𝑉
.
Now, solve this problem using simplex method
Problem is
The problem is converted to canonical form by adding
slack, surplus and artificial variables as appropriate
Max Zq = y1+ y2+ y3
subject to
5 y1+3y2+7y3≤1
7 y1+9y2+ y3≤1
10y1+6y2+2y3≤1
and y1,y2,y3≥0;

42.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
42
1. As the constraint-1 is of type '≤' we should add slack
variable S1
2. As the constraint-2 is of type '≤' we should add slack
variable S2
3. As the constraint-3 is of type '≤' we should add slack
variable S3
After introducing slack variables
Iteration-1 Cj 1 1 1 0 0 0
B CB XB Y1 Y2 Y3 S1 S2 S3
MinRatio
XB/y1
S1 0 1 5 3 7 1 0 0
1
5
S2 0 1 7 9 1 0 1 0
1
7
S3 0 1 (10) 6 2 0 0 1
1
10
→
Zq=0 Zj 0 0 0 0 0 0
Cj-Zj 1↑ 1 1 0 0 0
Max Zq = y1+ y2+ y3+0s1+0s2+0s3
subject to constraints
5 y1+3y2+7y3+s1=1
7 y1+9y2+ y3+s2=1
10y1+6y2+2y3+s3=1
and y1,y2,y3,s1,s2,s3≥0
 The initial solution is shown in below table.

43.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
43
Positive maximum Cj-Zj is 1 and its column index is 1.
So, the entering variable is y1.
Minimum ratio is
1
10
and its row index is 3. So, the
leaving basis variable is S3.
∴ The pivot element is 10.
Iteration-2 Cj 1 1 1 0 0 0
B CB XB y1 y2 y3 S1 S2 S3
MinRatio
XB/y3
S1 0
1
2
0 0 (6) 1 0 −
1
2
1
2
6
=
1
12
=0.0833→
S2 0
3
10
0
24
5
−
2
5
0 1 −
7
10
---
y1 1
1
10
1
3
5
1
5
0 0
1
10
1
10
1
5
=
1
2
=0.5
Zq=
𝟏
𝟏𝟎
Zj 1
𝟑
𝟓
𝟏
𝟓
0 0
𝟏
𝟏𝟎
Cj-Zj 0
𝟐
𝟓
𝟒
𝟓
↑ 0 0 −
𝟏
𝟏𝟎
Positive maximum Cj-Zj is
4
5
and its column index is 3.
So, the entering variable is y3.
Minimum ratio is 0.0833 and its row index is 1. So, the
leaving basis variable is S1.

44.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
44
∴ The pivot element is 6.
Iteration
-3
Cj 1 1 1 0 0 0
B CB XB y1 y2 y3 S1 S2 S3
MinRatio
XB/y2
y3 1
1
12
0 0 1
1
6
0 −
1
12
---
S2 0
1
3
0 (
𝟐𝟒
𝟓
) 0
1
15
1 −
11
15
1
3
24
5
=
5
72
=
0.0694→
y1 1
1
12
1
3
5
0 −
1
30
0
7
60
1
12
3
5
=
5
36
= 0.1389
Zq=
𝟏
𝟔
Zj 1
𝟑
𝟓
1
𝟐
𝟏𝟓
0
𝟏
𝟑𝟎
Cj-Zj 0
𝟐
𝟓
↑ 0 −
𝟐
𝟏𝟓
0 −
𝟏
𝟑𝟎
Positive maximum Cj-Zj is
2
5
and its column index is 2.
So, the entering variable is y2.
Minimum ratio is 0.0694 and its row index is 2. So, the
leaving basis variable is S2.
∴ The pivot element is (
𝟐𝟒
𝟓
)

45.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
45
Iteration
-4
Cj 1 1 1 0 0 0
B CB XB y1 y2 y3 S1 S2 S3
MinRatio
XB/S3
y3 1
1
12
0 0 1
1
6
0 −
1
12
---
y2 1
5
72
0 1 0
1
72
5
72
−
11
72
---
y1 1
1
24
1 0 0 −
1
24
−
1
8
(
𝟓
𝟐𝟒
)
1
24
5
24
=
1
5
=
0.2→
Zq=
𝟕
𝟑𝟔
Zj 1 1 1
𝟓
𝟑𝟔
𝟏
𝟏𝟐
−
𝟏
𝟑𝟔
Cj-Zj 0 0 0 −
𝟓
𝟑𝟔
−
𝟏
𝟏𝟐
𝟏
𝟑𝟔
↑
Positive maximum Cj-Zj is
1
36
and its column index is 6.
So, the entering variable is S3.
Minimum ratio is 0.2 and its row index is 3. So, the
leaving basis variable is y1.
∴ The pivot element is (
𝟓
𝟐𝟒
).

46.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
46
Iteration-5 Cj 1 1 1 0 0 0
B CB XB y1 y2 y3 S1 S2 S3 MinRatio
y3 1
1
10
2
5
0 1
3
20
−
1
20
0
y2 1
1
10
11
15
1 0 −
1
60
7
60
0
S3 0
1
5
24
5
0 0 −
1
5
−
3
5
1
Zq=
𝟏
𝟓
Zj
𝟏𝟕
𝟏𝟓
1 1
𝟐
𝟏𝟓
𝟏
𝟏𝟓
0
Cj-Zj −
𝟐
𝟏𝟓
0 0 −
𝟐
𝟏𝟓
−
𝟏
𝟏𝟓
0
Since all Cj-Zj≤0
Hence, optimal solution is arrived with value of
variables as:
y1=0,y2=
1
10
,y3=
1
10
Max Zq=
1
5
∴Zq=1/V=
1
5
∴V=
1
1
5
=5

47.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
47
But, here constant k = 4 was added to all the elements
of pay-off matrix.
So expected value of the game is Z=V-k=5-4=1
Player B's optimal strategy
q1=V×y1=5×0=0
q2=V×y2=5×
1
10
=
1
2
q3=V×y3=5×
1
10
=
1
2
Hence, player B's (B1, B2, B3) optimal strategy
is (0,
1
2
,
1
2
).
Player A's optimal strategy
The values for x1, x2, x3 can be obtained from the
(cj-zj) row of final simplex table
x1=
2
15
, x2=
1
15
, x3=0
p1=V×x1=5×
2
15
=
2
3
p2=V×x2=5×
1
15
=
1
3
p3=V×x3=5×0=0

48.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
48
Hence, player A's (A1, A2,A3) optimal strategy is (
2
3
,
1
3
,0).
So, finally player B's (B1, B2, B3) optimal strategy
is (0,
1
2
,
1
2
),
And player A's (A1, A2, A3) optimal strategy is (
2
3
,
1
3
,0),
And Value of game is V=1.

49.  Theory of Game
SHREE M.P. SHAH ARTS AND SCIENCE COLLEGE
SURENDSRANAGAR
49
Reference
 Book
6TH
EDITION OPERATIONS RESEARCH THEORY AND
APPLICATION BY JK SHARMA
 Website
1)http://www.slideshare.net/neelamkushwaha904
/game-theory-47179069?from_m_app=android
2)http://www.slideshare.net/RushabhShah350/ga
me-theory-operation-research-
241185431?from_m_app=android
3)https://youtu.be/m8QYjaF4WPA