Dokumen ini membahas praktikum analisis regresi sederhana dengan tujuan agar mahasiswa dapat menentukan model regresi, melakukan pengujian hipotesis, dan menginterpretasikan output. Materi mencakup hubungan antara variabel independen dan dependen, serta langkah-langkah analisis menggunakan SPSS. Uji keberartian model dan koefisien regresi diperinci dengan pengujian hipotesis dan analisis variansi.

1. PRAKTIKUM 3
ANALISIS REGRESI SEDERHANA
1. MINGGU KE : 6
2. PERALATAN : LCD
3. SOFTWARE : SPSS
4. TUJUAN :
Mahasiswa dapat menentukan model regresi sederhana, serta mampu melakukan
pengujian hipotesis untuk menguji keberartian dari model regresi yang diperoleh, selain itu
mahasiswa juga dapat menginterpretasikan hasil output dari analisis regresi sederhana.
5. TEORI PENGANTAR
Analisis regresi dipergunakan untuk mempelajari hubungan antara dua variabel atau
lebih, yang menjadi fokus adalah untuk menelusuri pola hubungan tersebut yang modelnya
belum diketahui dengan sempurna, atau untuk mengetahui bagaimana variasi dari beberapa
variabel independen mempengaruhi variabel dependen dalam suatu fenomena yang kompleks.
Apabila X1, X2, … , Xi adalah variabel-variabel independen dan Y adalah variabel dependen,
maka terdapat hubungan fungsional antara X dan Y, di mana variasi dari X akan diiringi pula
oleh variasi dari Y. Secara matematika hubungan di atas dapat dijabarkan sebagai berikut: Y
= f(X1, X2, …, Xi, e), di mana : Y adalah variabel dependen, X adalah variabel independen
dan e adalah variabel residu (disturbance term).
KOEFISIEN REGRESI SEDERHANA
Regresi sederhana, bertujuan untuk mempelajari hubungan antara dua variabel.
Model regresi sederhana adalah model regresi dengan satu variabel tak bebas dan satu
variabel bebas.
Model regresi sederhana untuk populasi :
Y = α + βX + ε
dengan, Y adalah variabel tak bebas, X adalah variabel bebas, α adalah intersep (perpotongan
garis dengan sumbu Y), β adalah koefisien regresi untuk variabel bebas, dan ε adalah
galat/error, diasumsikan berdistribusi normal dengan rata-rata 0 dan varians σ2.
Model regresi sederhana untuk sampel :
y = a + bX + ε
ˆ

2. ˆ
di mana, y adalah variabel tak bebas, X adalah variabel bebas, a adalah penduga bagi intersep
(α), b adalah penduga bagi koefisien regresi (β), dan α, β adalah parameter yang nilainya
tidak diketahui sehingga diduga menggunakan statistik sampel.
Rumus yang dapat digunakan untuk mencari a dan b adalah:
a=
∑Y − b∑ X = Y − bX
.N .
N .( ∑ X Y ) − ∑ X ∑Y
b=
.N .∑ X 2 − ( ∑ X )
2
Keterangan:
Xi = Rata-rata skor variabel X
Yi = Rata-rata skor variabel Y
UJI KEBERARTIAN PARSIAL PARAMETER REGRESI (UJI KEBERARTIAN INTERSEP)
Pemeriksaan keberartian parsial parameter regresi dilakukan melalui pengujian
hipotesis nol, bahwa intersep a sama dengan nol (tidak berarti) melawan hipotesis tandingan
bahwa intersep tidak sama dengan nol.
Pengujian hipotesis uintuk menguji apakah intersep yang diperoleh signifikan
digunakan uji t.
Perumusan hipotesis :
Ho : α = 0 : Intersep untuk model regresi sederhana tersebut tidak signifikan.
H1 : α ≠ 0 : Intersep untuk model regresi sederhana tersebut signifikan.
dengan uji statistik :
a −α
t hit =
sb
dengan: sb =
se SSE (∑ X ) 2
SS x
, se = , SS x = ∑ X − 2
n −2 n
SSE = ∑( y − y ) = ∑y 2 − a ∑y − b ∑xy
2
ˆ
Pengambilan keputusan menggunakan angka pembanding t tabel dengan kriteria
sebagai berikut:
t tabel = t  α 
 , n −2 
2 

3. o Jika t hitung < −t tabel atau t hitung > t tabel , maka H0 ditolak; H1 diterima
o Jika − t tabel ≤ t hitung ≤ t tabel , maka H0 diterima; H1 ditolak
Untuk pengujian dalam SPSS digunakan kriteria sebagai berikut:
o Jika angka signifikansi hasil riset < α, maka nilai intersep untuk model regresi
sederhana tersebut berarti, atau H0 ditolak; H1 diterima.
o Jika angka signifikansi hasil riset > α, maka nilai intersep untuk model regresi
sederhana tersebut tidak berarti, atau H0 diterima; H1 ditolak.
UJI KEBERARTIAN PARSIAL PARAMETER REGRESI (UJI KEBERARTIAN KOEFISIEN
REGRESI)
Pemeriksaan keberartian parsial parameter regresi dilakukan melalui pengujian
hipotesis nol, bahwa koefisien regresi b sama dengan nol (tidak berarti) melawan hipotesis
tandingan bahwa koefisien arah regresi tidak sama dengan nol.
Pengujian hipotesis uintuk menguji apakah koefisien regresi yang diperoleh
signifikan digunakan uji t.
Perumusan hipotesis :
Ho : β = 0 : Koefisien regresi untuk model regresi sederhana tersebut tidak signifikan.
H1 : β ≠ 0 : Koefisien regresi untuk model regresi sederhana tersebut signifikan.
dengan uji statistik :
b−β
t hit =
sb
dengan: sb =
se SSE (∑ X ) 2
SS x
, se = , SS x = ∑ X − 2
n −2 n
SSE = ∑( y − y ) = ∑y 2 − a ∑y − b ∑xy
2
ˆ
Pengambilan keputusan menggunakan angka pembanding t tabel dengan kriteria
sebagai berikut:
t tabel = t  α 
 , n −2 
2 
o Jika t hitung < −t tabel atau t hitung > t tabel , maka H0 ditolak; H1 diterima
o Jika − t tabel ≤ t hitung ≤ t tabel , maka H0 diterima; H1 ditolak
Untuk pengujian dalam SPSS digunakan kriteria sebagai berikut:

4. o Jika angka signifikansi hasil riset < α, maka nilai koefisien regresi untuk model regresi
sederhana tersebut berarti, atau H0 ditolak; H1 diterima.
o Jika angka signifikansi hasil riset > α, maka nilai koefisien regresi untuk model regresi
sederhana tersebut tidak berarti, atau H0 diterima; H1 ditolak.
UJI KEBERARTIAN MODEL REGRESI
Pemeriksaan keberartian model regresi dilakukan melalui pengujian hipotesis nol,
bahwa intersep serta koefisien regresi sama dengan nol melawan hipotesis tandingan bahwa
intersep serta koefisien regresi tidak sama dengan nol.
Pengujian keberartian model regresi dilakukan dengan menggunakan pendekatan
analisis variansi (ANOVA) yaitu dengan menguraikan komponen-komponen total keragaman
dari variabel terikat.
Langkah-langkah uji keberartian model regresi dapat disederhanakan dalam sebuah
tabel anova sebagai berikut :
Tabel 1
Analisis of Varians
Sumber Variasi df SS MS Fhitung Ftabel
Intersep 1 SSI SSI
MSI =
1
Regresi 1 SSR SSR MSR F(α, 1, n −2 )
MSR = Fhit =
1 MSE
Residual n-2 SSE SSE
MSE =
n −2
Total n SST SST
MST =
n
Keterangan:
( ∑Y ) 2
SSI =
n

SSR = b.∑XY −
∑X .∑Y 

 n 
 

5.  Y 2 − ( ∑Y )
 2

SST = ∑ 
 n 
 
SSE = SST − SSR
Pengujian hipotesis uintuk menguji apakah koefisien regresi yang diperoleh
signifikan digunakan uji F.
Perumusan hipotesis :
Ho : Β = 0 : Model regresi tidak bearti.
H1 : Β ≠ 0 : Model regresi berarti.
Β = [α, β]
dengan uji statistik :
MSR
Fhit =
MSE
Pengambilan keputusan menggunakan angka pembanding F tabel dengan kriteria
sebagai berikut:
Ftabel = F(α,1, n −2 )
o Jika Fhitung ≥ Ftabel , maka H0 ditolak; H1 diterima
o Jika Fhitung < Ftabel , maka H0 diterima; H1 ditolak
Untuk pengujian dalam SPSS digunakan kriteria sebagai berikut:
o Jika angka signifikansi hasil riset < α, maka model regresi yang diperoleh berarti, atau
H0 ditolak; H1 diterima.
o Jika angka signifikansi hasil riset > α, maka model regresi yang diperoleh tidak
berarti, atau H0 diterima; H1 ditolak.
6. LANGKAH KERJA
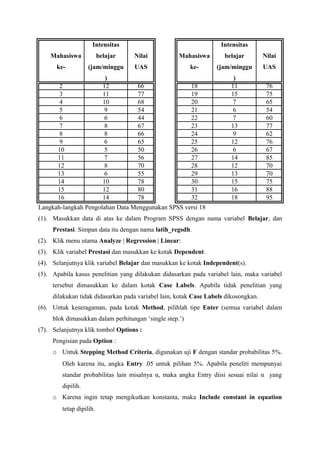
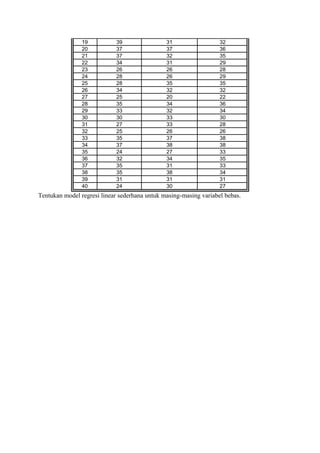
Contoh kasus, seorang peneliti ingin mengetahui pola hubungan fungsional antara
intensitas belajar (diukur dari lamanya belajar dalam 1 minggu) dengan prestasi mata kuliah
statistika dasar (diukur dari nilai ujian akhir semester). Data yang diperoleh sebanyak 32 data
sebagai berikut:
Intensitas Intensitas
Mahasiswa belajar Nilai Mahasiswa belajar Nilai
ke- (jam/minggu UAS ke- (jam/minggu UAS
) )
1 6 65 17 16 90

6. Intensitas Intensitas
Mahasiswa belajar Nilai Mahasiswa belajar Nilai
ke- (jam/minggu UAS ke- (jam/minggu UAS
) )
2 12 66 18 11 76
3 11 77 19 15 75
4 10 68 20 7 65
5 9 54 21 6 54
6 6 44 22 7 60
7 8 67 23 13 77
8 8 66 24 9 62
9 6 65 25 12 76
10 5 50 26 6 67
11 7 56 27 14 85
12 8 70 28 12 70
13 6 55 29 13 70
14 10 78 30 15 75
15 12 80 31 16 88
16 14 78 32 18 95
Langkah-langkah Pengolahan Data Menggunakan SPSS versi 18
(1). Masukkan data di atas ke dalam Program SPSS dengan nama variabel Belajar, dan
Prestasi. Simpan data itu dengan nama latih_regsdh.
(2). Klik menu utama Analyze | Regression | Linear:
(3). Klik variabel Prestasi dan masukkan ke kotak Dependent.
(4). Selanjutnya klik variabel Belajar dan masukkan ke kotak Independent(s).
(5). Apabila kasus penelitian yang dilakukan didasarkan pada variabel lain, maka variabel
tersebut dimasukkan ke dalam kotak Case Labels. Apabila tidak penelitian yang
dilakukan tidak didasarkan pada variabel lain, kotak Case Labels dikosongkan.
(6). Untuk keseragaman, pada kotak Method, pilihlah tipe Enter (semua variabel dalam
blok dimasukkan dalam perhitungan ‘single step.’)
(7). Selanjutnya klik tombol Options :
Pengisian pada Option :
o Untuk Stepping Method Criteria, digunakan uji F dengan standar probabilitas 5%.
Oleh karena itu, angka Entry .05 untuk pilihan 5%. Apabila peneliti mempunyai
standar probabilitas lain misalnya α, maka angka Entry diisi sesuai nilai α yang
dipilih.
o Karena ingin tetap mengikutkan konstanta, maka Include constant in equation
tetap dipilih.

7. o Klik Continue untuk meneruskan langkah.
(8). Pilih kolom Statistics dengan mengklik pilihan tersebut.
(9). Klik Estimates, Descriptive dan Model fit.
(10). Pada kolom Residuals, klik pada Casewise diagnostics, dan dari situ dipilih all cases
untuk melihat pengaruh regresi terhadap keseluruhan. Kemudian klik Continue.
(11). Pilih Plots untuk melihat grafik untuk regresi.
(12). Klik pilihan SDRESID dan masukkan ke pilihan Y. Klik pilihan ZPRED dan masukkan
ke pilihan X. Setelah kedua variabel X dan Y terisi, klik tombol Next untuk melanjutkan
pengisian plot kedua.
(13). Tampak variabel Y dan X kosong kembali. Sekarang klik pilihan ZPRED dan
masukkan ke Y dan klik pilihan DEPENDENT masukkan ke pilihan X.
(14). Untuk plot ketiga, pilihlah Standardized Residual Plots, kliklah pada Normal
Probability Test.
(15). Selanjutnya klik Continue
(16). Klik OK.
(17). Hasil pengolahan data akan muncul pada Output Navigator.
7. TUGAS
Berdasarkan data rekapitulasi hasil penelitian, dimana seorang peneliti ingin
mengetahui pola hubungan antara prestasi kerja dengan gaya kepemimpinan, dan prestasi
kerja dengan motivasi kerja. Data yang diperoleh sebanyak 40 data, berikut ini :
No. Kepemimpinan Motivasi Kerja Prestasi Kerja
Resp (X1) (X2) (Y)
1 35 36 34
2 31 34 32
3 40 39 36
4 24 26 24
5 20 25 26
6 39 37 39
7 32 38 37
8 40 35 37
9 32 36 36
10 43 43 40
11 42 40 39
12 37 32 32
13 23 20 25
14 35 43 41
15 41 38 39
16 42 38 39
17 31 33 31
18 36 35 33

8. 19 39 31 32
20 37 37 36
21 37 32 35
22 34 31 29
23 26 26 28
24 28 26 29
25 28 35 35
26 34 32 32
27 25 20 22
28 35 34 36
29 33 32 34
30 30 33 30
31 27 33 28
32 25 26 26
33 35 37 38
34 37 38 38
35 24 27 33
36 32 34 35
37 35 31 33
38 35 38 34
39 31 31 31
40 24 30 27
Tentukan model regresi linear sederhana untuk masing-masing variabel bebas.

9. DAFTAR PUSTAKA
Gujarati, Damodar N. 1988. Basic Econometrics. New York, USA, McGraw-Hill.
Hosmer, David W, and Stanley Lemeshow. 2000. Applied Logistic Regression, New York,
USA, John Wiley & Sons.
http://www.jonathansarwono.info/korelasi/korelasi.htm
http://samianstats.files.wordpress.com/2008/10/korelasional-spss1.pdf
http://guruvalah.20m.com/kasus_penelitian_korelasi.pdf
Nachrowi D. N. And Usman D., 2008, Penggunaan Teknik Ekonometri, Jakarta, PT.
RajaGrafindo Persada
Uyanto, S., S., 2009, Pedoman Analisis Data dengan SPSS, Yogyakarta, Graha Ilmu.
Suharjo, B., 2008, Analisis Regresi Terapan dengan SPSS, Yogyakarta, Graha Ilmu.