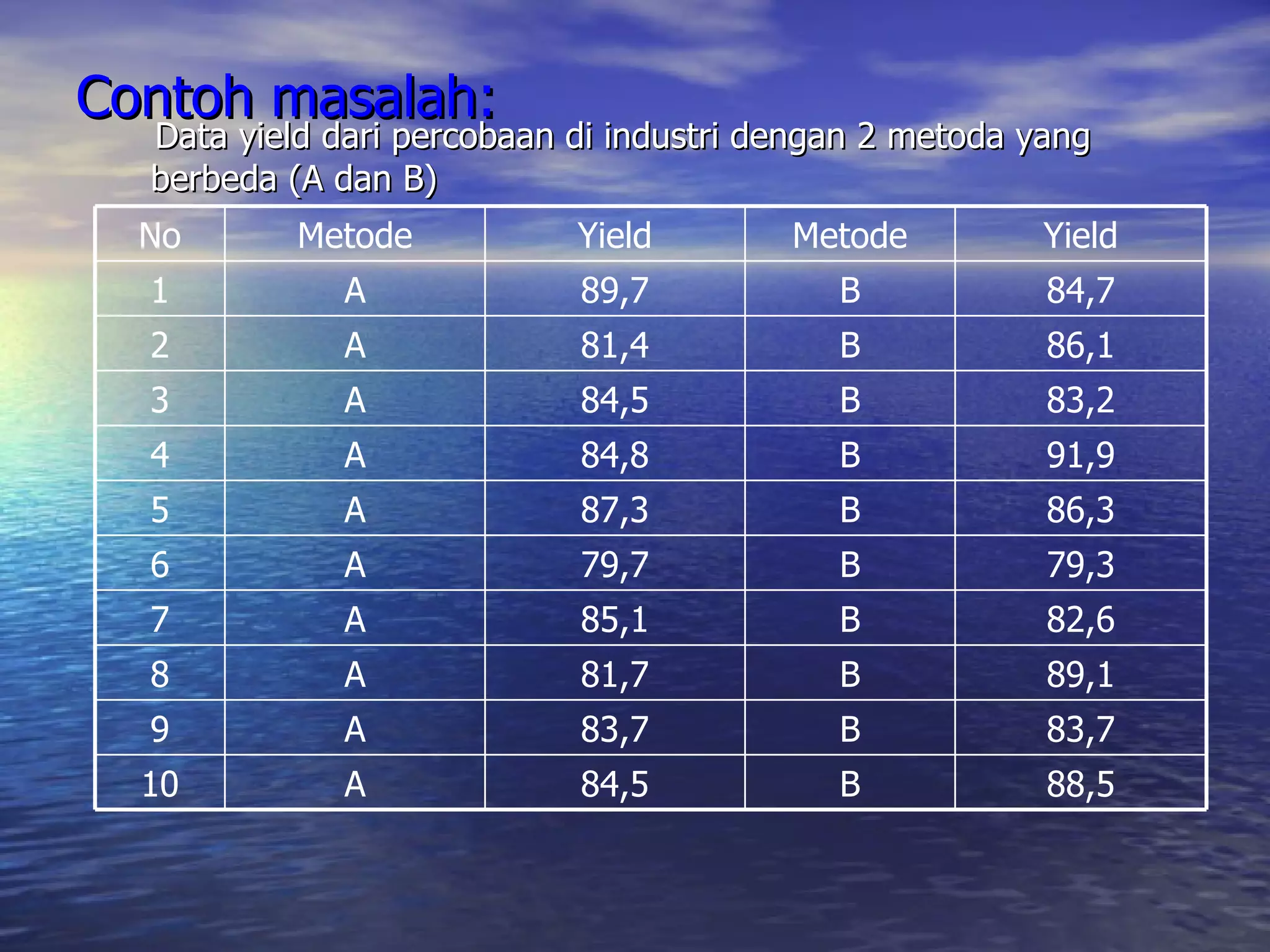
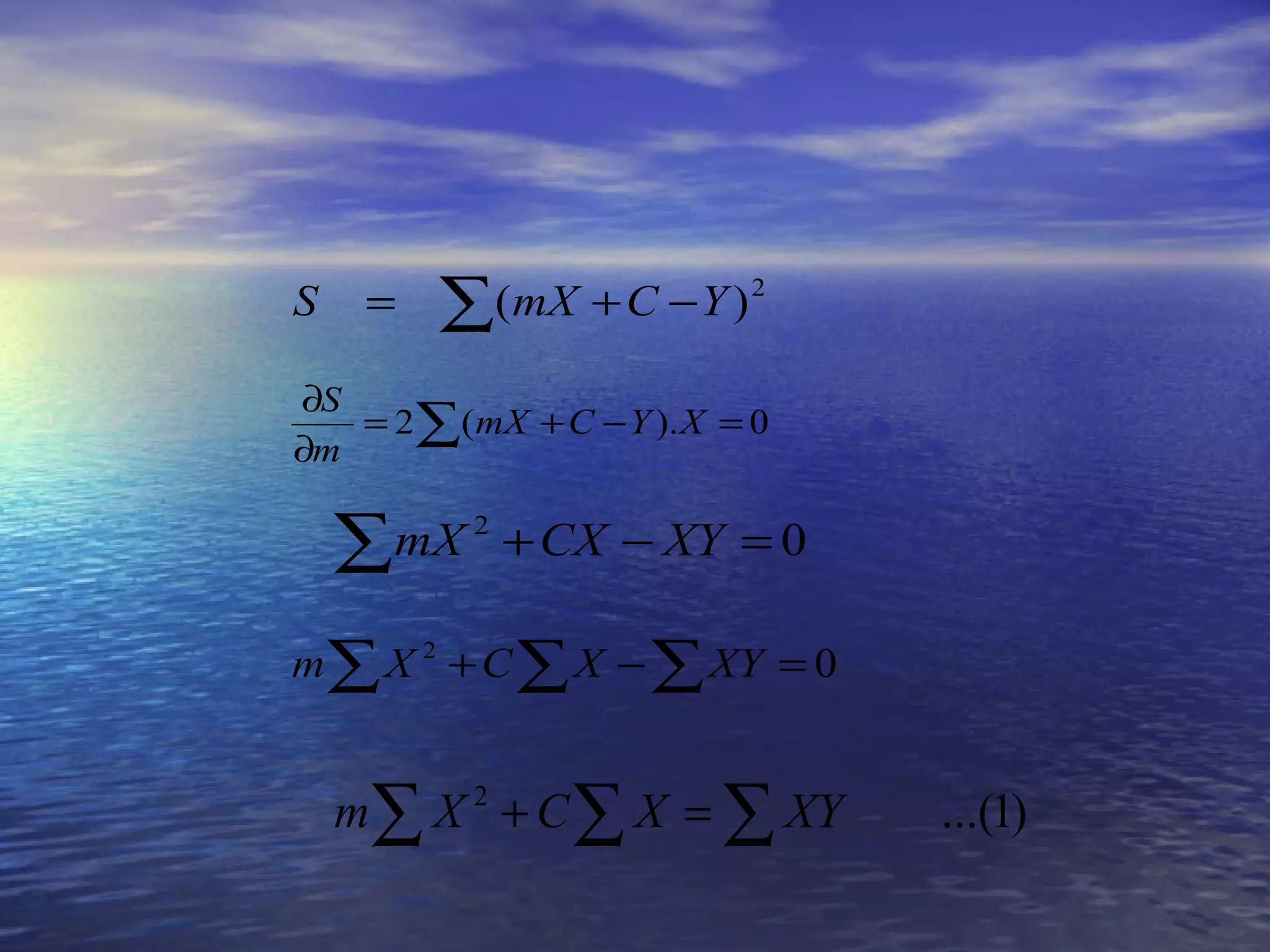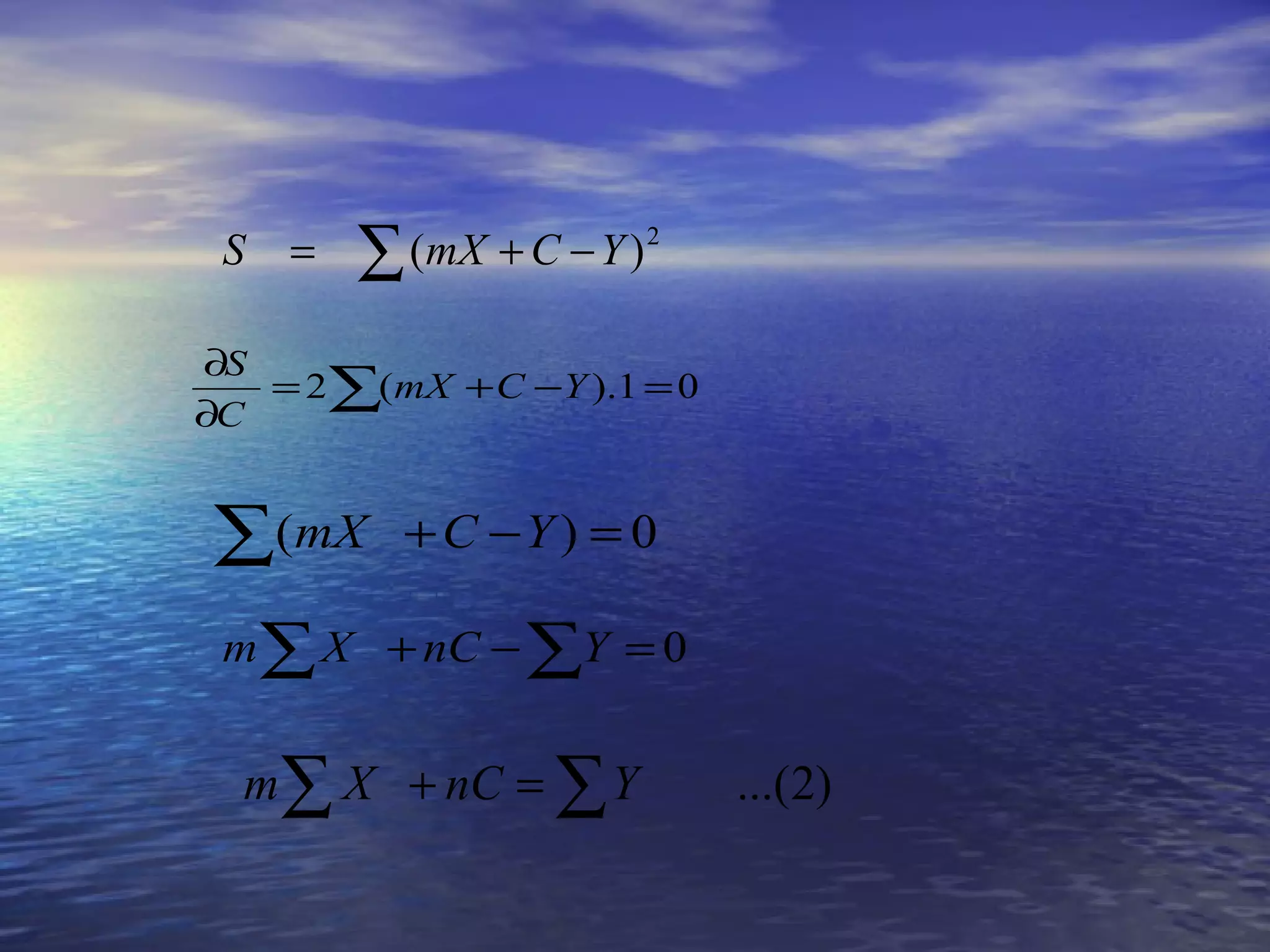Dokumen ini membahas teknik pemodelan dan analisis hubungan antar variabel melalui regresi dan analisis korelasi. Pembahasan meliputi koefisien korelasi, regresi linear sederhana, regresi linear berganda, serta analisis komparatif untuk membandingkan data dari dua kelompok atau lebih. Terdapat juga penjelasan mengenai analisis deskriptif yang digunakan untuk menguji generalisasi hasil penelitian.

1. PEMODELAN SEDERHANA DENGAN REGRESI Dengan pemodelan ----  bisa memperkirakan bagaimana hubungan antara variabel yang ada ----  pertanyaan : seberapa cocok model yang disusun terhadap data yang diperoleh ??? ===  perlu topik mengenai ANALISIS HUBUNGAN

2. ANALISIS HUBUNGAN Yaitu bentuk analisis variabel (data) penelitian untuk untuk mengetahui : Derajat atau kekuatan hubungan Bentuk atau arah hubungan di antara variabel2 Besarnya pengaruh variabel yang satu (var. bebas) terhadap variabel lainnya (var. terikat).

3. TEKNIK STATISTIK DALAM ANALISIS HUBUNGAN ANALISIS KORELASI (KOEFISIEN KORELASI KOEFISIEN PENENTU (KOEF. DETERMINASI ANALISIS REGRESI (PERSAMAAN REGRESI ===  baik untuk hubungan yang melibatkan 2 variabel atau lebih

4. ANALISIS HUBUNGAN ANTARA 2 VARIABEL 1. KOEFISIEN KORELASI (KK) adalah indeks atau bilangan yang digunakan untuk mengukur derajat hubungan, meliputi kekuatan hubungan dan bentuk/arah hubungan Untuk kekuatan hubungan : KK antara 0 dan +1 KK = 0 tidak ada hubungan KK = 1 sempurna 0,9 < KK < 1,00 sangat tinggi, kuat sekali 0,7 <KK < 0,9 tinggi atau kuat 0,4 < KK < 0,7 cukup atau sedang, dsb Untuk bentuk/arah hubungan, + =  Y naik terhadap kenaikan X - =  Y turun terhadap penurunan X

5. KOEFISIEN KORELASI PEARSON r = koefisien korelasi Pearson X = variabel bebas Y = variabel terikat

6. ANALISIS HUBUNGAN ANTARA 2 VARIABEL 2. KOEFISIEN PENENTU (KP) adalah angka / indeks yang digunakan untuk mengetahui besarnya sumbangan sebuah variabel lebih (var. bebas, X) terhadap variabel lainnya (var. terikat, Y) KP = (KK) 2 X 100 %

7. 3. REGRESI linear sederhana Regresi : teknik analisis hubungan yang digunakan untuk meramalkan atau memperkirakan nilai dari suatu variabel dalam hubungannya dg variabel yang lain melalui suatu persamaan ==  bisa pers. linear dan non linear Regresi linear sederhana : regresi linear dimana variabel yang terlibat hanya 2, yaitu variabel terikat Y dan variabel bebas X, serta berpangkat 1

8. Bentuk persamaannya : Y = mX + C X = variabel bebas Y variabel terikat (variabel yang diduga) C = intersep m = koefisien regresi (slope)

9. Jumlah kuadrat kesalahan =  minimal Sum of square error (S) =  minimal Least square S = Jumlah(Y-Ym)2 =  minimal

10. REGRESI LINEAR SEDERHANA (2 VARIABEL) Y P = mX + C =  seberapa dekat persamaan pendekatan Y P dengan data hasil percobaan Y dan X ?? Jumlah kuadrat kesalahan (S) antara Y P dan Y harus minimal

11. Barapa nilai m dan C agar S minimal ??? =  berlaku

14. Substitusi dari pers (1) dan (2) =  2 persamaan dengan 2 bilangan tak diketahui ==  m dan C bisa ditentukan

15. ANALISIS HUBUNGAN LEBIH 2 VARIABEL Koefisien korelasi untuk 3 variabel =  Y = f(X 1 , X 2 ) Atau KP = R Y1,2 2 x 100 %

16. 2. Koefisien korelasi 4 variabel ===  Y = f (X1, X1, X3) Koefisien Penentu KP = R 2 Y1,2 x 100 %

17. KOEFISIEN KORELASI PARSIAL 3 VARIABEL 1. Koef. Korelasi parsial Y dan X1 bila X2 konstan Koef. Penentu parsial Y dan X1 bila X2 konstan KP = r 2 Y1,2 x 100 %

18. 2. Koef. Korelasi parsial Y dan X2 bila X1 konstan Koef. Penentu parsial Y dan X2 bila X1 konstan KP = r 2 Y2,1 x 100 %

19. 2. Koef. Korelasi parsial X1 dan X2 bila Y konstan Koef. Penentu parsial X1 dan X2 bila Y konstan KP = r 2 Y12 x 100 %

20. REGRESI LINEAR BERGANDA 3 VARIABEL Y = f(x 1 , x 2 ) Misal Y = a + b 1 X 1 + b 2 X 2 ===  bila diturunkan akan diperoleh 3 persamaan dengan 3 bilangan tak diketahui a, b1, b2

21. ANALISIS KOMPARATIF = analisis komparasi = analisis perbedaan = analisis variabel (data) untuk mengetahui perbedaan antara dua kelompok data (variabel) atau lebih =  teknik statistik yang digunakan = uji statistik yaitu pengujian hipotesis komparatif =  sering disebut UJI SIGNIFIKANSI ( test of significance )

22. Contoh analisis komparatif 1. sampel yang bekorelasi perbandingan kemampuan kerja pegawai sebelum dan sesudah diberi pelatihan Perbandingan nilai pretest dan posttest Perbandingan kelompok eksperimen dengan kelompok kontrol Perbadingan yield reaksi kimia antara katalis A dan katalis B dll

23. Contoh analisis komparatif 2. sampel yang tidak bekorelasi Perbandingan kinerja Reaktor Fixed Bed dengan Reaktor Fluidized bed Perbandingan pendapatan dosen dengan pegawai Perbandingan IP mahasiswa Teknik Kimia dengan mahasiswa Teknik Sipil

24. Analisis komparatif 2 sampel berkorelasi ==  Uji statistik t untuk data interval/rasio Menentukan formulasi hipotetis a. Ho : tidak perbedaan positif antara kelompok I dan II H1 : ada perbedaan positif antara kelompok I dan II b. Ho tidak ada perbedaan negatif H1 : ada perbedaan negatif c. Ho : tidak perbedaan H1 ada perbedaan 2. Menentukan taraf nyata ( α ) dan t tabel 3. Menentukan kriteria pengujian

25. 4. Menentukan nilai uji statistik X = rata2 skor kelompok I Y = rata skor kelompok II D = jumlah skor kelompok I dan II N = jumlah data 5. Membuat kesimpulan =  menyimpulkan Ho diterima atau tidak

26. Contoh masalah: Data yield dari percobaan di industri dengan 2 metoda yang berbeda (A dan B) 88,5 B 84,5 A 10 83,7 B 83,7 A 9 89,1 B 81,7 A 8 82,6 B 85,1 A 7 79,3 B 79,7 A 6 86,3 B 87,3 A 5 91,9 B 84,8 A 4 83,2 B 84,5 A 3 86,1 B 81,4 A 2 84,7 B 89,7 A 1 Yield Metode Yield Metode No

27. Masalah : Dari dua metoda yang digunakan, apakah ada perbedaan yang signifikan?? Bila ada perbedaan, metode manakah yang lebih baik??

28. Analisa komparatif k (lebih dr 2) sampel berkorelasi Anova 1 arah; dg 1 faktor berpengaruh: - Anova 1 arah dengan sampel sama banyaknya - anlova 1 arah dg sampal tidak sama banyaknya 2. Anova 2 arah; dg 2 faktor berpengaruh

29. ANALISIS DESKRIPTIF Merupakan bentuk analisis data untuk menguji generalisasi hasil penelitian yang didasarkan atas satu sampel Dilakukan melalui uji hipotesis deskriptif Hasil analisa : apakah hipotesis penelitian dapat digeneralisasikan atau tidak Menggunakan satu variabel atau lebih tapi bersifat mandiri ==  TIDAK BERBENTUK PERBANDINGAN ATAU HUBUNGAN

30. Contoh analisis deskriptif Penelitian untuk IP kumulatif rata-rata mahasiswa Teknik Kimia. Untuk itu diambel 50 sampel IP mahasiswa. =  ujilah hipotesis yang mengatakan bahwa IPK rata-rata mahasiswa Teknik Kimia adalah 3,2.