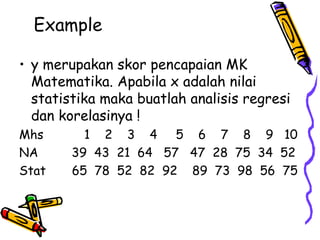
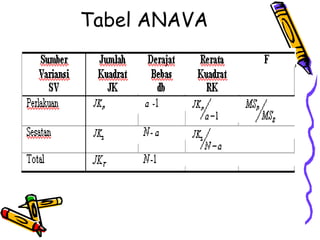
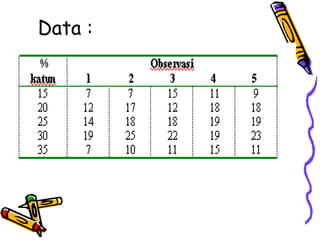
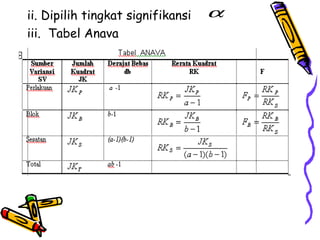
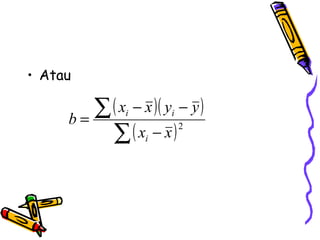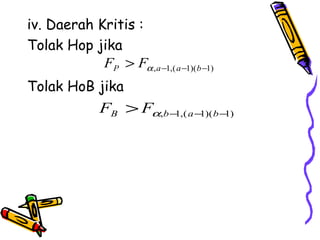Statistika parametrik digunakan untuk melakukan inferensi terhadap rata-rata populasi, membandingkan dua rata-rata populasi, dan menganalisis hubungan antar variabel menggunakan korelasi dan regresi. Metode ini meliputi penggunaan uji-z, uji-t, uji-F, dan analisis regresi linier untuk memodelkan hubungan antara variabel tergantung dan bebas.

1. Selayang Pandang
Statistika
Parametrik

2. Berbagai Metode Parametrik
a. Inferensi terhadap sebuah rata-rata
populasi
 sampel besar, gunakan rumus z
 sampel kecil (<30), gunakan student t test
b. Inferensi terhadap dua rata-rata populasi
 Sampel besar, gunakan z test yang
dimodifikasi
 Sampel kecil, gunakan t test yang
dimodifikasi atau F test

3. c. Inferensi untuk mengetahui hubungan antar
variabel
> Hubungan antar Dua Variabel, meng
gunakan metode korelasi dan Regresi
sederhana
> Hubungan antar lebih dari dua variabel,
menggunakan metode korelasi dan regresi
berganda

4. Analisis Regresi
dan Korelasi

5. Regresi Sederhana dan Korelasi
o Analisis hubungan di antara kedua
variabel/lebih  analisis Regresi dan
Korelasi.
o Dalam analisis Regresi, akan
dikembangkan sebuah persamaan regresi
yaitu formula matematika yang mencari
nilai variabel tergantung (dependent) dari
nilai variabel bebas (independent) yang
diketahui.
o Analisa regresi terutama digunakan untuk
tujuan peramalan.

6. Model Matematika yang
digunakan :
• Garis Lurus
• Parabola / Kurva Kuadratik
• Kurva kubik
• Kurva Quartic
• Kurva pangkat n
• Biasanya disebut sebagai polinomial
berderajat satu, dua, ….dst

7. Metoda Garis Lurus
• y= a + bx

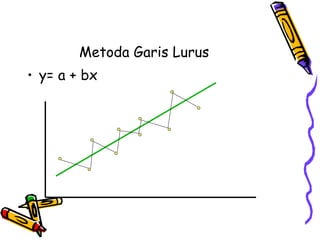
8. • Xi variabel independen ke-i
• Yi variabel dependen ke-i maka bentuk model
regresi sederhana adalah :
Yi = α + β X i + ε i , i = 1,2,, n
dengan
α , β parameter yang tidak diketahui
εi sesatan random dgn asumsi
E[ε i ] = 0
Var (ε i ) = σ 2

9. • Bentuk model di atas diprediksi
berbentuk :
ˆ
Yi = a + bX i
• dengan a dan b koefisien regresi
merupakan penaksir α, β
Dengan Metode Kuadrat terkecil
diperoleh :
a = y − bx
( ∑ y )( ∑ x )
∑ yx −
i i
n
i i
b=
( ∑ xi ) 2
∑ xi − n
2

10. • Atau
b=
∑ ( x − x )( y − y )
i i
∑( x − x)
2
i

11. • Perhatikan
( y − y ) = ( yˆ − y )+ ( y − yˆ )
i i i i
var iasi regresi sisa
∑(y ) (
− y = ∑ yi − y + ∑ ( yi − yi ) )
2 2 2
i
ˆ ˆ
JKT JKR JKS

12. • Tabel Anava :
Sumber JK dk RK F Hitung
Variasi
Regresi JKR 1 RKR=JKR/1 RKR/RKS
Sesatan JKS n-2 RKS=JKS/n-2 F(alpha,
1,n-2)
Total JKT n-1

13. Dalam analisis regresi & ANAVAlangkah-langkah yang dapat dilakukan antara
lain :
1. ek Asumsi : kenormalan, independensi dan homogenitas
C
2. enentukan prediksi model regresi dan Koefisien regresi
M
3. Menentukan koefisien korelasi R2
4. Membuat Tabel Anava
5. Pemeriksaan sisa data
6. Menentukan Korelasi Sederhana

14. Uji Hipotesa koefisien regresi
• H 0 : β = 0 vs H 1 : β ≠ 0
• Dipilih tingkat signifikansi
• Hitung Tabel Anava
• Tolak Ho jika
FHitung > Fα,1, n −2
tingkat signifikansi > Sig.
• Untuk uji satu sisi :
FHitung > Fα ,1,n − 2 = t 2
n−2

15. Korelasi
• Menyatakan hubungan antara dua
atau lebih peubah  asosiasi
• Bila dua peubah tidak berhubungan ;
korelasinya 0, bila sempurna
korelasinya 1 (kolinier)

16. • Koefisien korelasi dinotasikan dengan R2
• Setelah ditaksir persamaan regresi dari data
masalah berikutnya adalah menilai
baik/buruknya kecocokan model dengan data
• Rumus :
JKR
R =
2
JKT
∑ ( yi − y )
2
ˆ
=
∑ ( yi − y )
2
0 ≤ R2 ≤ 1

17. Aplikasi Regresi dengan SPSS.
• 1. Pilih menu Analyze – Regression – Linear
• 2. Tentukan var bergantung dan var bebas
• 3. Tentukan Metoda yang digunakan (Enter,
Stepwise,Forward, Backward)
• 4. Tentukan perhitungan statistik yang diperlukan
• 5. Tentukan jenis plot yang diperlukan
• 6. Tentukan harga F testnya
•

18. Example
• y merupakan skor pencapaian MK
Matematika. Apabila x adalah nilai
statistika maka buatlah analisis regresi
dan korelasinya !
Mhs 1 2 3 4 5 6 7 8 9 10
NA 39 43 21 64 57 47 28 75 34 52
Stat 65 78 52 82 92 89 73 98 56 75

19. Analisis SPSS 16.0
Nilai rata-rata nilai akhir 46 dan nilai
rata-rata statistika dari 10 mahasiswa
adalah 76

20. Korelasi atau hubungan antara nilai akhir dan
nilaistatistika adalah 0.84, jadi hubungannya
sangat erat (mendekati1).
Hasil didukung dengan (misal) α = 0.05 > 0.001
maka H0 bahwa antara variabel y (NA) dengan
x (Nilai Statistika) tidak berhubungan ditolak.

21. R square=0.705 mengindikasinya besarnya
hubungan antara NA dengan nilai statistika
sebesar 70.5%.

22. Uji Hipotesa koefisien regresi
• H 0 : β = 0 vs H 1 : β ≠ 0
• Dipilih tingkat signifikansi =0.05
• Hitung Tabel Anava
• Tolak Ho jika
FHitung =19.141 > F0.05,1,8 =5.32
α = 0.05 > Sig. = 0.002

23. • D.k.l : terdapat hubungan linier
antara variabel dependen (y) dengan
variabel independen (x)

24. Model linier yang terbentuk antara variabel y
(Nilai Akhir) dengan nilai statistika (x) adalah
y = −24.012 + 0.921x
ˆ

25. ANAVA SATU ARAH
Rancangan random lengkap karena
unit eksperimen yang dipergunakan
dianggap sama/seragam
Satu Arah karena 1 faktor yang
diselidiki

26. • Model RRL :
 i = 1, 2,K , a
yij = µ + τ i + ε ij 
 j = 1, 2,K , n
dengan
a = perlakuan ,
n = banyak observasi,
µ
= rata-rata,
τ
= efek perlakuan ke-i,
i

27. Uji F
• Analisa efek perlakuan ke-i (untuk
model efek tetap)
i. Hipotesis H 0 : τ i = 0, untuk semua i
H 1 : Tidak semua τ i = 0
ii. Dipilih tingkat signifikansi α
iii. Tabel ANAVA

28. Tabel ANAVA

29. iv. Daerah Kritis :
Tolak Ho jika F > Fα ,a −1, N − a
Atau Tolak Ho jika α > Sig.

30. Example
• Akan diteliti pengaruh kadar serat
katun sintetis terhadap kualitas daya
rentang kain tersebut. Dipilih 5 serat
katun dengan kadar prosentase 15%,
20%, 25%, 30% dan 35%. Anggap
tingkat signifikansi 0.05. Diambil 5
observasi secara acak untuk tiap
perlakuan, diperoleh data :

31. Data :

32. ANAVA Dua Arah
• Jika unit percobaan sangat heterogen dan
dapat dikelompokkan ke dalam blok- blok
yang lebih homogen maka menggunakan
Rancangan Blok Random Lengkap ( RBRL )
lebih menguntungkan daripada Rancangan
Random Lengkap ( RRL ) karena selain
efisien waktu eksperimen juga bertujuan
menghilangkan sumber yang menyebabkan
variasi sesatan dari eksperimen.

33. • Model :
 i = 1,2, , a
y ij = µ + τ i + β j + ε ij 
 j = 1,2, , b
y ij
• adalah observasi untuk perlakuan
µ
ke- i dalam blok ke- j, rata-rata βj
τi
keseluruhan, efek perlakuan ke-i,
efek blok ke- j

34. Uji F
• Langkah-langkah :
• Analisa efek perlakuan ke-i
H 0 P : µ i = 0, untuk semua i
H 1P : Tidak semua µ i = 0
Analisa efek blok ke- j
H 0B : τ 1 = τ 2 =  = τ a = 0
H 1B : τ i ≠ 0, untuk suatu i

35. ii. Dipilih tingkat signifikansi α
iii. Tabel Anava

36. iv. Daerah Kritis :
Tolak Hop jika
FP > Fα ,a −1,( a −1)(b −1)
Tolak HoB jika
FB > Fα,b −1,( a −1)( b −1)

37. Example
• Akan diselidiki pengaruh tiga metode
(penentu premi maksimum) terhadap
tingkat kepercayaan pemegang polis
asuransi. Dipilih 50 pemegang polis asuransi
untuk memberikan skala kepercayaan
terhadap masing- masing metode dengan
skala 0 untuk tidak percaya sepenuhnya
sampai skala 20 untuk nilai sangat percaya.
Kelimapuluh orang tersebut dibagi dalam
lima macam eksekutif sebagai blok
berdasarkan peringkat usia dan diperoleh
data sebagai berikut :

38. gunakan tingkat signifikansi 0.01, untuk
menganalisa data di bawah ini :