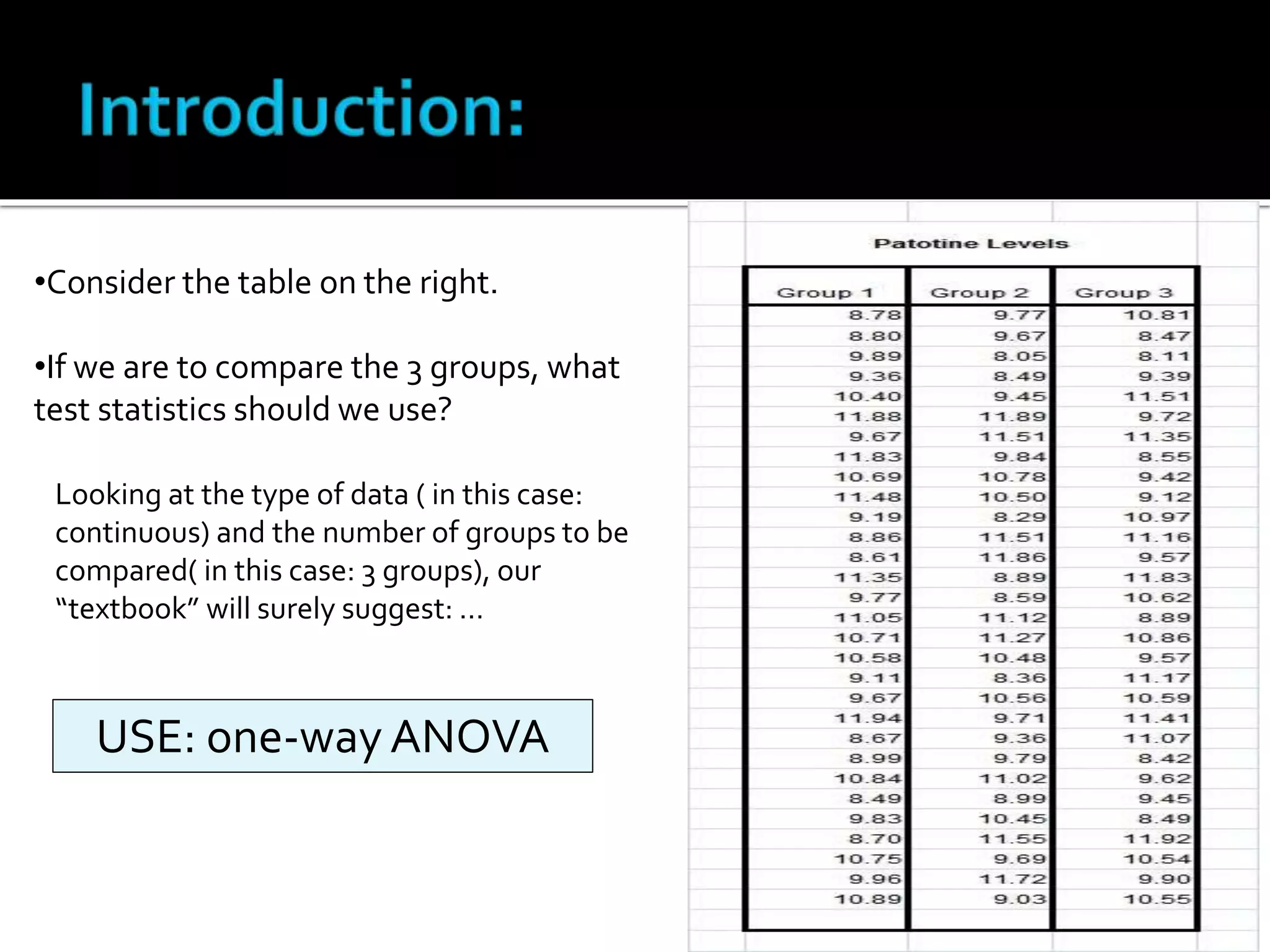
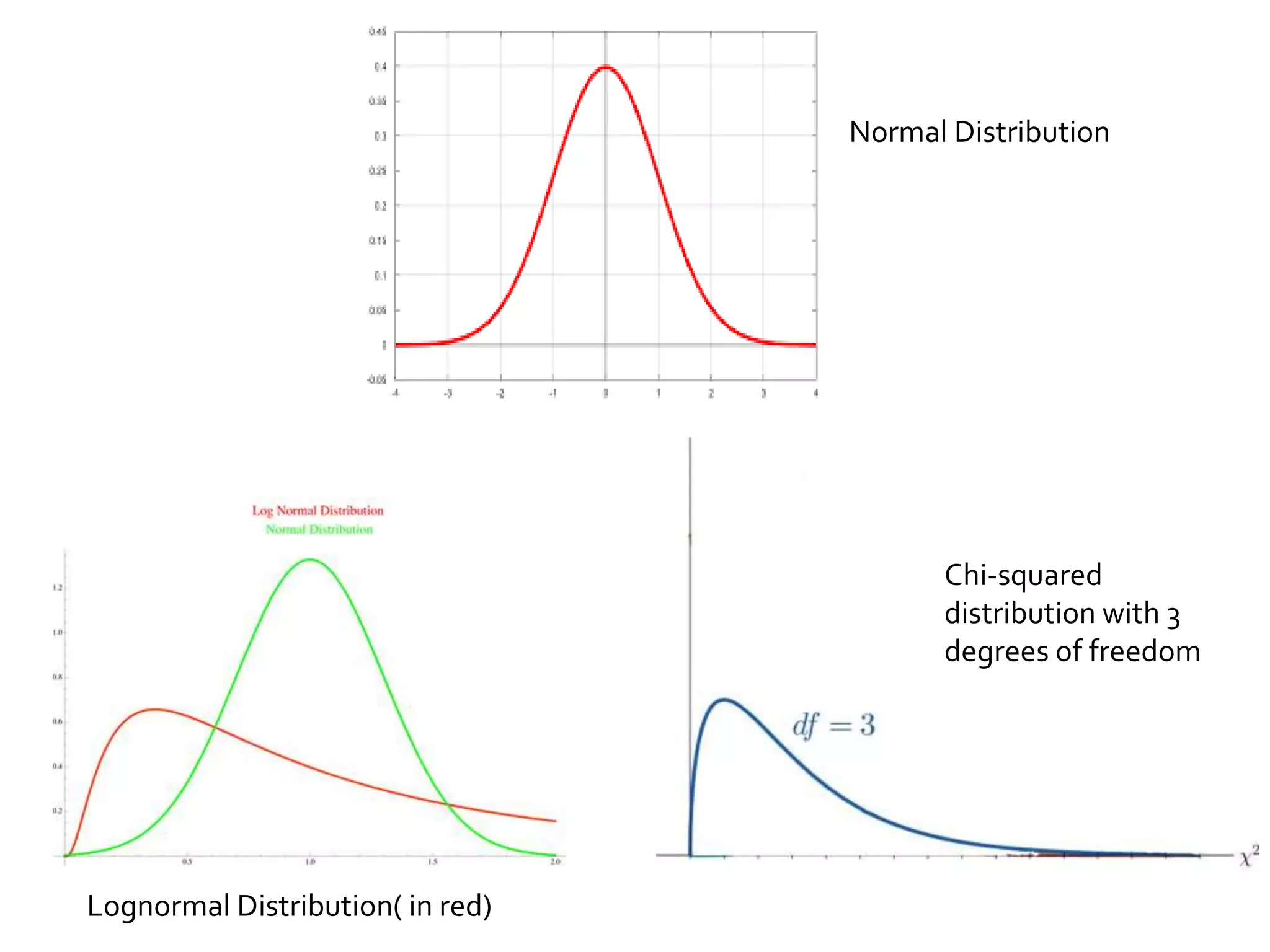
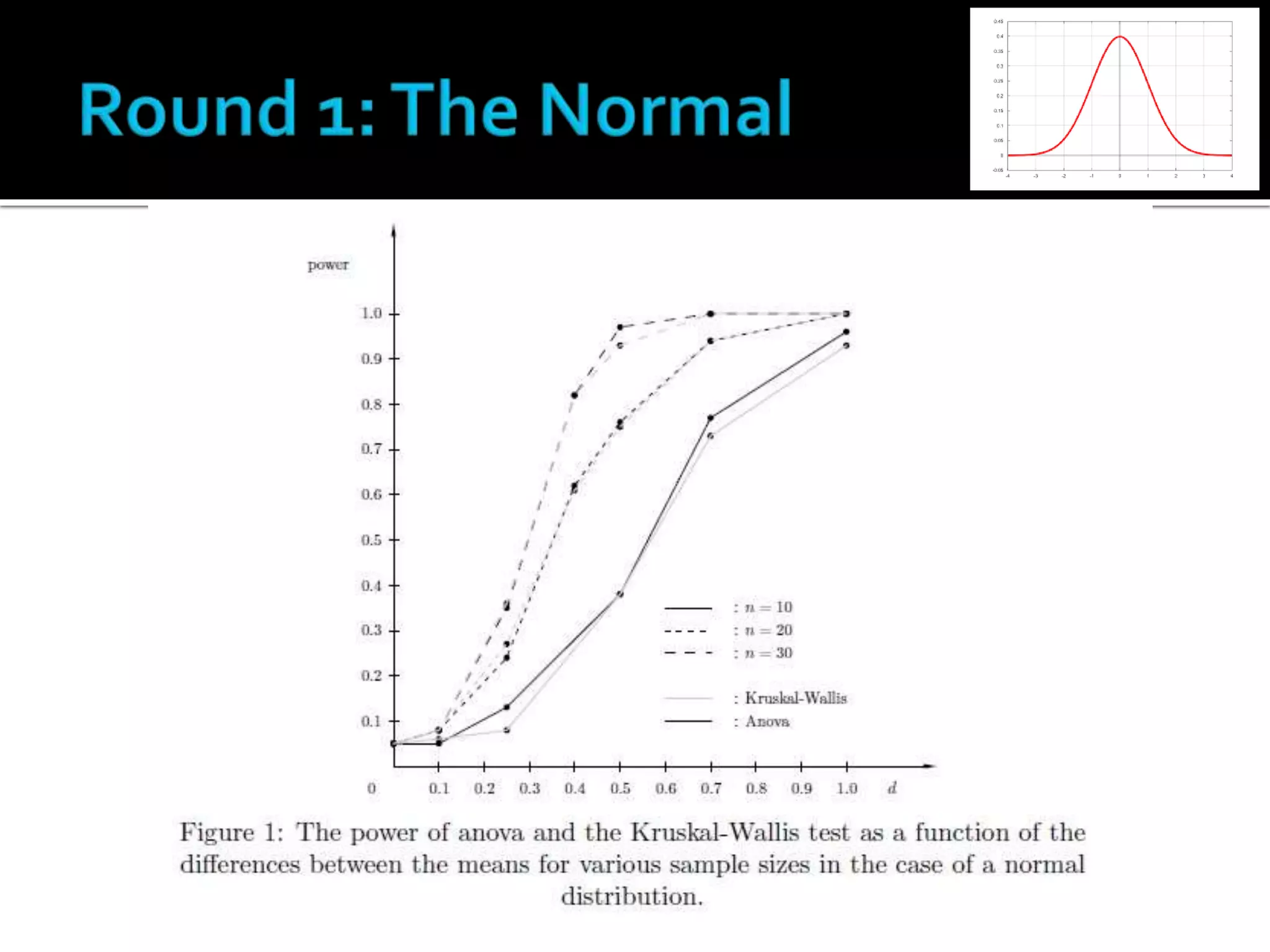
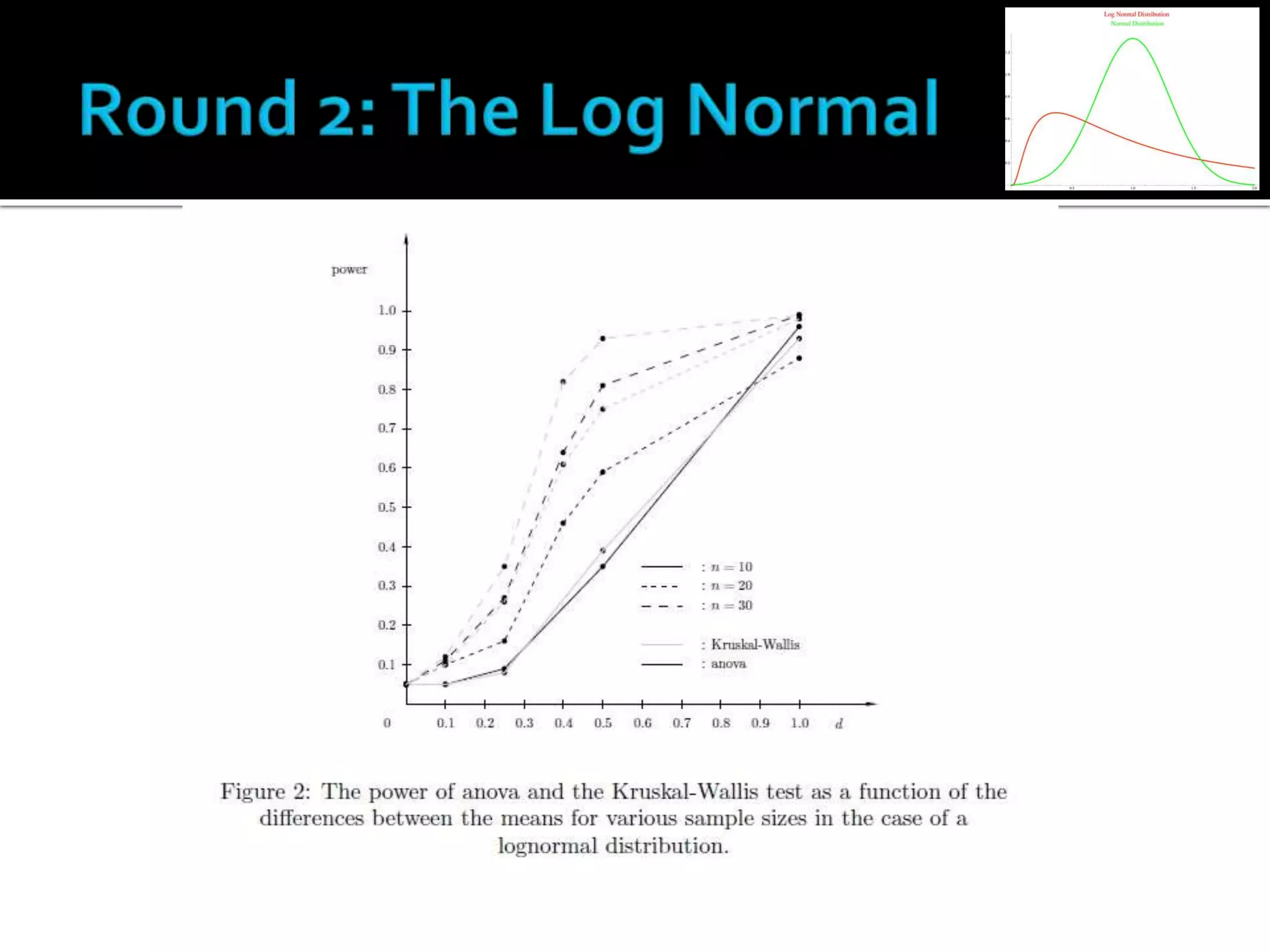
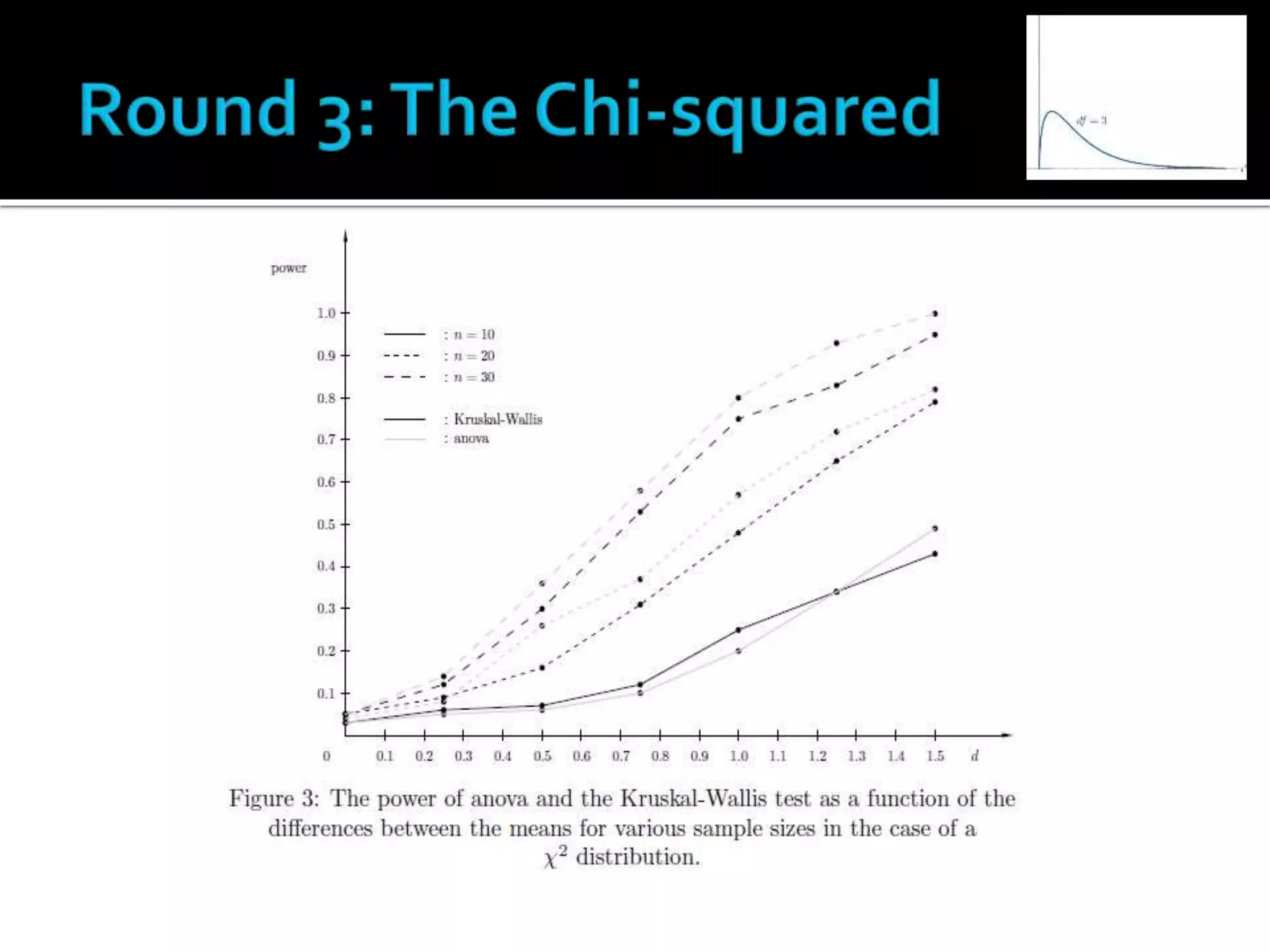
This paper compared the ANOVA and Kruskal-Wallis tests in situations where the assumption of normality is violated. Through Monte Carlo simulations with normally distributed, lognormally distributed, and chi-squared distributed data, the paper found that when the data is asymmetrically distributed, the non-parametric Kruskal-Wallis test has higher power to detect differences between groups than the parametric ANOVA test. The results show that checking assumptions like normality is important before choosing a test, as the power of ANOVA can significantly decrease when the normality assumption is violated.

1. “Monday Journal Activity”

2. A Parametric test A Non-parametric test
“Many-sample location parameter tests” bout

3. TanjaVan Hecke
Faculty of Applied Engineering Sciences,
Ghent University,
Ghent ,Belgium
Tanja.VanHecke@hogent.be
Presented by:
Mr. Benito Jr. B. Cuanan
Scientific Publishing and Statistics Department
Strategic Center for Diabetes Research
King Saud University

4. Suppose levels of Patotine (a non-existing hormone) of
different groups are being investigated.
Suppose the groups are: “the underweight
group” , “the normal group” and “the
overweight group”. Once data are collected,
how should this three groups be compared?

5. -----The most common approach would be to
compare the mean or median levels of the
different groups.
But how?
Take note:
It would be very awkward if in your
research paper, you present your data
like this:
“ … figures in table 1.1 are the Tukey’s
Biweight m-estimator…”

6. •Consider the table on the right.
•If we are to compare the 3 groups, what
test statistics should we use?
Looking at the type of data ( in this case:
continuous) and the number of groups to be
compared( in this case: 3 groups), our
“textbook” will surely suggest: …
USE: one-way ANOVA

7. Are you sure
about that?
Have you checked
the normality?
How about its
scedasticity?

8. This paper described the comparison of the
ANOVA and the Kruskal-Wallis test by means
of the power when violating the assumption
about normally distributed populations. The
permutation method is used as a simulation
method to determine the power of the test. It
appears that in the case of asymmetric
populations, the non-parametric Kruskal-Wallis
test performs better than the parametric
equivalent ANOVA method.

9.  A parametric test
 The most commonly used test for location.
 Used to analyze the differences between group means and
their associated procedures.
 It models the data as:
yij= μi + εij ,
μi is the mean or expected response of data in
the i-th treatment.
εij are independent, identically
distributed normal random errors.

10. The one-way ANOVA is used to test the
equality of k (k > 2) population
means, so the null hypothesis is:
H0 : μ1 = μ2 = . . . = μk.
Assumptions:
1. The dependent variable is
normally distributed in each group
that is being compared.
2. There is homogeneity of
variances. This means that the
population variances in each group
are equal.
What if the
assumptions are
violated?
one-way ANOVA may yield
inaccurate estimates of the p-value
when the data are not
normally distributed at all.
If the sample sizes are equal
or nearly equal, ANOVA is very
robust. If not, then the true p-value
is greater than the
computed p-value.

11. This paper focused on the violation of the
first(in our list) assumption of ANOVA,
that is: violation on NORMALITY of each
group’s distribution.

12.  A Non-parametric test
 The “analogue” of ANOVA in testing for location.
 Used to compare the medians of 3 or more independent
groups.
 It models the data as:
yij = ηi + φij ,
ηi is the median response of data in the i-th
treatment.
φij are independent, identically
distributed continuous random errors

13.  Unlike the ANOVA, this test does not make assumptions
about normality. However, it assumes that each group have
approximately the same shape.
 Like most non-parametric tests, it is performed on the ranks
of the measurement observations.
 The null hypothesis of the Kruskal-Wallis test states that the
samples are from identical populations.
 When rejecting the null hypothesis of the Kruskal-Wallis test,
then at least one of sample stochastically dominates at least
one other sample.

14. POWER:
 Statistical power is defined as the probability that the test
correctly rejects the null hypothesis when the null hypothesis
is false.
 It is the “sensitivity” of the test.
 In this paper, empirical power were calculated.

15. PERMUTATION TEST:
The steps for a multiple-treatment permutation test:
• Compute the F-value of the given samples, called Fobs.
• Re-arrange the k n observations in k samples of size n.
• For each permutation of the data, compare the F-value with the Fobs
For the upper tailed test, compute the p-value as
p =#(F >Fobs)/ntot
If the p-value is less than or equal to the predetermined level of
significance α, then we reject H0.
 if we have 3 groups with 20 observations each, there are (60!)(20!)-3
possible different permutations of those observations into three
groups.
 That’s equivalent to 577,831,814,478,475,823,831,865,900

16. The Monte Carlo simulation was used.
 random data from a specified distribution with given
parameters were generated.
 ANOVA and Kruskal-Wallis test were then conducted.
 2500 samples from chosen distributions were tested
at α = 0.05.

17.  The following hypotheses were considered:
Ho : μ1 = μ2 = μ3
and
H1 : μ1 + d = μ2 and μ1 + 2d = μ3
Ex. @d=0.3:
if μ1 = 1 , then μ2 =1.3 and μ3 =1.6
 The two tests were compared in 3 distribution types,
namely: Normal, Lognormal, and Chi-squared
distribution.

18. Normal Distribution
Chi-squared
distribution with 3
degrees of freedom
Lognormal Distribution( in red)

22.  For non-symmetrical distributions, the non-parametrical
Kruskal-Wallis test results in a higher
power compared to the classical one-way anova.
 The results of the simulations show that an
analysis of the data is needed before a test on
differences in central tendencies is conducted.
 Although the literature and textbooks state that
the F-test is robust under the violations of
assumptions, these results show that the power
suffers a significant decrease.