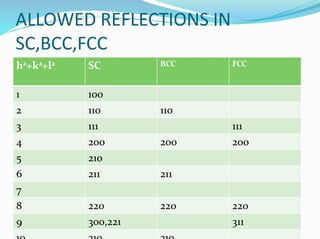
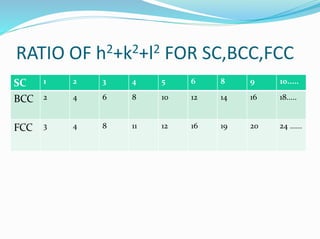
This document discusses powder X-ray diffraction (XRD), including Miller indices for describing crystal planes, Bragg's law relating diffraction and plane spacing, systematic absences due to crystal structure, determining structure from XRD patterns, and applications and limitations of the technique. Key components of an XRD diffractometer are described. The process of indexing diffraction patterns to determine the unit cell type and parameters is outlined.

1. BY ,
JAYABRATA DAS
ROLL-99/05/PG-III ,NO – 150021
REGN. NO -28-0605, UNIVERSITY OF NORTH
BENGAL

2. OUTLINE
 1. WHAT ARE MILLER INDICES
 2. HOW BRAGG’S LAW AND REFLECTION FROM
PLANES ARE RELATED
 SELECTION RULES OF REFLECTIONS FOR
VARIOUS LATTICES
 BRIEF INTRDUCTION TO DIFFRACTOMETER
 HOW TO OBTAIN LATTICE STRUCTURE FROM
POWRER-XRD DATA
 APPLICATIONS
 LIMITATIONS

3. MILLER INDICES (h,k,l)
Miller indices are notations for describing and
labelling planes in crystals and lattices.

4. BRAGG’S LAW IS A NECESSARY BUT INSUFFICIENT
CONDITION FOR DIFFRACTION
BRAGG’S EQN. IS A NEGATIVE STATEMENT-
If Bragg’s eqn is not satisfied- No Reflection can occur
If Bragg’s eqn is satisfied – Reflection ‘MAY’ occur
The presence of additional atom in the unit cell
Is the reason for missing Reflection ,known as
‘SYSTEMETIC ABSENCES’

5. Reflection from some planes are missing in
the below BCC unit cell
 path difference between
 green rays is λ so they are in
 phase but between green
 and red rays are λ/2,so they
 out of phase and reflection
 from 100 (red) plane is not
 observed.

6. THE REFLECTIONS PRESENT AND MISSING
REFLECTIONS IN CUBIC SYSTEM
BRAVAIS LATTICE REFLECTIONS WHICH
MAY BE P
RESENT
REFLECTION WHICH
NECESSARILY ABSENT
SC ALL NONE
BCC (h+ k+l ) even (h+k+l) ODD
FCC h, k, l unmixed h, k, l mixed

7. ALLOWED REFLECTIONS IN
SC,BCC,FCC
h2+k2+l2 SC BCC FCC
1 100
2 110 110
3 111 111
4 200 200 200
5 210
6 211 211
7
8 220 220 220
9 300,221 311

8. RATIO OF h2+k2+l2 FOR SC,BCC,FCC
SC 1 2 3 4 5 6 8 9 10.....
BCC 2 4 6 8 10 12 14 16 18.....
FCC 3 4 8 11 12 16 19 20 24 ......

10.  d- spacing in cubic system – 1/d2 =h2+k2+l2/a2
 and Bragg’s eqn. n λ= 2dsin θ
 Combining this two sin2 θ =( λ2/4a2) (h2+k2+l2)
 So sin2 θ is propotional to h2+k2+l2 , which can be used
to determine lattice parameters.

11. MODERN DIFFRACTOMETER

12. ESSENTIAL PARTS OF
DIFFRACTOMETER
 1. X-RAY TUBE
 2. INCIDENT BEAM OPTICS
 3.THE GONIOMETER
 4. THE SAMPLE AND SAMPLE HOLDER
 5.RECIEVING SIDE OPTICS
 6. DETECTOR

13. DETERMINING CRYSTAL
STRUCTURE
 A Diffraction pattern cannot be analyzed until it has
been ‘INDEXED’.
 1.Manual Indexing 2.Autoindexing
 Two methods of indexing
 a. Mathematical b.Analytical

14. STEPS TO FOLLOW FOR
MATHEMATICAL INDEXING
 1. Identify the peaks.
 2. Determine sin2θ
 3. Calculate the ratio of sin2θ/sin2θmin and multiply by the
appropriate integers
 4. Select result from (3) that yields h2+k2+l2 as integers

 5.Compare results with the sequences of h2+k2+l2
 values to idetify the Bravais lattice
 6. calculate lattice parameters

15. NUMBER OF PEAKS DEPENDS ON
 WAVELENGTH OF X-RAY
 LATTICE TYPE
 SYMMETRY OF THE CRYSTAL

16. APPLICATIONS
 BRAVAIS LATTICE DETERMINATION
 LATTICE PARAMETER DETERMINATION
 DETERMINE IF MATERIAL IS AMORPHOUS OR
CRYSTALLIE
 PHASE COMPOSITION OF A SAMPLE
 CRYSTALLITE SIZE AND STRAIN
 QUANTITATIVE PHASE ANALYSIS

17. LIMITATIONS
 ELEMENTAL ANALYSIS
 ONLY SMALL FRACTION OF CRYSTALLITES IN
SAMPLE CONTRIBUTE TO DIFFRACTION PATTERN

18. ACKNOWLEDGEMENT
 I AM VERY GREATEFUL TO Dr. ASHIS
KUMAR NANDA FOR ASSISTING ME
DURING THE PREPARATION OF
SEMINAR.
 I AM ALSO THANKFUL TO OUR HEAD OF
DEPARTMENT Prof. BASUDEB BASU ,ALL
OTHER TEACHERS OF DEPARTMENT ,MY
FRIENDS AND WELL WISHERS FOR
SUPPORTING ME.

19. REFERENCE
 POWDER X-RAY DIFFRACTION ,MIT (PDF)
http://prism:mit.edu/x-ray
.X-RAY DIFFRACTION ,UNIVERSITY OF
NORTH CAROLLINA (PDF)
.MTE ,CLASS17 X-RAY DIFFRACTION

20. 
 THANK YOU