Allan Gulinao, profile picture
Uploaded byAllan Gulinao
DOCX, PDF1,604 views

Graph of polynomial function

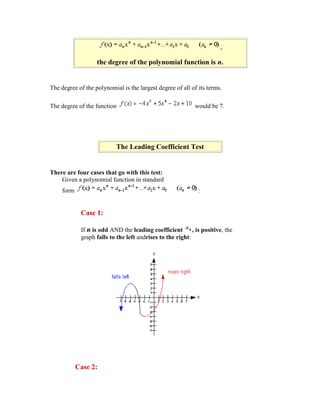
The document discusses graphing polynomial functions. It begins by stating the learning objectives, which include identifying polynomial functions, using the leading coefficient test to determine graph end behavior, finding zeros, determining zero multiplicity, knowing the maximum number of turning points, and graphing polynomial functions. It then provides an introduction and definitions of key polynomial function concepts like leading term, leading coefficient, degree of a term and function, and the leading coefficient test. The document uses examples to demonstrate how to apply the leading coefficient test and find zeros and their multiplicities. It states that a polynomial can have at most n-1 turning points if it has degree n. Finally, it outlines the steps to graph a polynomial function.

Embed presentation

Downloaded 27 times
Learning Objectives After completing this tutorial, you should be able to: 1. Identify a polynomial function. 2. Use the Leading Coefficient Test to find the end behavior of the graph of a given polynomial function. 3. Find the zeros of a polynomial function. 4. Find the multiplicity of a zero and know if the graph crosses the x-axis at the zero or touches the x-axis and turns around at the zero. 5. Know the maximum number of turning points a graph of a polynomial function could have. 6. Graph a polynomial function. Introduction In this tutorial we will be looking at graphs of polynomial functions. If you need a review on functions, feel free to go to Tutorial 30: Introduction to Functions. If you need a review on polynomials in general, feel free to go to Tutorial 6: Polynomials. Basically, the graph of a polynomial function is a smooth continuous curve. There are several main aspects of this type of graph that you can use to help put the curve together. I will be going over how to use the leading term of your polynomial function to determine the end behavior of its graph. We will also be looking at finding the zeros, aka the x-intercepts, as well as the y-intercept of the graph. If you need a review on intercepts, feel free to go to Tutorial 26: Equations of Lines. Another important concept is to know the largest possible number of turning points. This will help you be more accurate in the graph that you draw. That just about covers it. I guess you are ready to get to it.
Tutorial Polynomial Function A polynomial function is a function that can be written in the form , where are real numbers and n is a nonnegative integer. Basically it is a function whose rule is given by a polynomial in one variable. If you need a review on functions, feel free to go to Tutorial 30: Introduction to Functions. If you need a review on polynomials in general, feel free to go to Tutorial 6: Polynomials. An example of a polynomial function is . Leading Term When the polynomial function is written in standard form, , the leading term is .
In other words, the leading term is the term that the variable has its highest exponent. The leading term of the function would be . Leading Coefficient When the polynomial function is written in standard form, , the leading coefficient is . Basically, the leading coefficient is the coefficient on the leading term. The leading coefficient of the function would be - 4. Degree of a Term of a Polynomial Function The degree of a term of a polynomial function is the exponent on the variable. Degree of a Polynomial Function When the polynomial function is written in standard form,
, the degree of the polynomial function is n. The degree of the polynomial is the largest degree of all of its terms. The degree of the function would be 7. The Leading Coefficient Test There are four cases that go with this test: Given a polynomial function in standard form : Case 1: If n is odd AND the leading coefficient , is positive, the graph falls to the left andrises to the right: Case 2:
If n is odd AND the leading coefficient , is negative, the graph rises to the left andfalls to the right. Case 3: If n is even AND the leading coefficient , is positive, the graph rises to the left and to the right. Case 4:
If n is even AND the leading coefficient , is negative, the graph falls to the left and to the right. Example 1: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!! Second question is what is the leading term’s degree? If you said 3, you are right on!! 3 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said 5, pat yourself on the back!!
Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 3, is odd and the leading coefficient, 5, is positive, then the graph of the given polynomial falls to the left and rises to the right. Example 2: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!! Second question is what is the leading term’s degree? If you said 4, you are right on!! 4 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said -1, pat yourself on the back!! Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 4, is even and the leading coefficient, -1, is negative, then the graph of the given polynomial falls to the left and falls to the right.
Example 3: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!! Second question is what is the leading term’s degree? If you said 5, you are right on!! 5 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said -7, pat yourself on the back!! Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 5, is odd and the leading coefficient, -7, is negative, then the graph of the given polynomial rises to the left and falls to the right. Example 4: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!!
Second question is what is the leading term’s degree? If you said 6, you are right on!! 6 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said 1, pat yourself on the back!! Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 6, is even and the leading coefficient, 1, is positive, then the graph of the given polynomial rises to the left and rises to the right. Zeros (or Roots) of Polynomial Functions A zero or root of a polynomial function is the value of x such that f(x) = 0. In other words it is the x-intercept, where the functional value or y is equal to 0. Zero of Multiplicity k If is a factor of a polynomial function f and is not a factor of f, then r is called a
zero of multiplicity k of f. In other words, when a polynomial function is set equal to zero and has been completely factored and each different factor is written with the highest appropriate exponent, depending on the number of times that factor occurs in the product, the exponent on the factor that the zero is a solution for, gives the multiplicity of that zero. The exponent indicates how many times that factor would be written out in the product, this gives us a multiplicity. Multiplicity of Zeros and the x-intercept There are two cases that go with this concept: Case 1: If r is a zero of even multiplicity: This means the graph touches the x-axis at r and turns around. This happens because the sign of f(x) does not change from one side to the other side of r. Case 2: If r is a zero of odd multiplicity: This means the graph crosses the x-axis at r. This happens because the sign of f(x) changes from one side to the other side of r.
Turning Points If f is a polynomial function of degree n, then there is at most n - 1 turning points on the graph of f. A turning point is a point at which the graph changes direction. Keep in mind that you can have fewer than n - 1 turning points, but it will never exceed n - 1 turning points. Example 5: Find the zeros for the polynomial function and give the multiplicity for each zero. Indicate whether the graph crosses the x-axis or touches the x-axis and turns around at each zero. First Factor: The first factor is 3, which is a constant. Therefore, there are no zeros that go with this factor. Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = -1/2 is a zero
What would the multiplicity of the zero x = -1/2 be? If you said the multiplicity for x = -1/2 is 4, you are correct!!!! Since the exponent on this factor is 4, then its multiplicity is 4. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = -1/2? If you said it touches the x-axis and turns around at the zero x = -1/2, pat yourself on the back!!! It does this because the multiplicity is 4, which is even. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = 4 is a zero What would the multiplicity of the zero x = 4 be? If you said the multiplicity for x = 4 is 3, you are correct!!!! Since the exponent on this factor is 3, then its multiplicity is 3. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = 4? If you said it crosses the x-axis at the zero x = 4, pat yourself on the back!!! It does this because the multiplicity is 3, which is odd. Example 6: Find the zeros for the polynomial
function and give the multiplicity for each zero. Indicate whether the graph crosses the x-axis or touches the x-axis and turns around at each zero. Let’s factor this one first: *Factor out a GCF *Factor a diff. of squares First Factor: *Setting the 1st factor = 0 *Solve for x *x = 0 is a zero What would the multiplicity of the zero x = 0 be? If you said the multiplicity for x = 0 is 2, you are correct!!!! Since the exponent on this factor is 2, then its multiplicity is 2. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = 0? If you said it touches the x-axis and turns around at the zero x = 0, pat yourself on the back!!! It does this because the multiplicity is 2, which is even. Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = -3 is a zero
What would the multiplicity of the zero x = -3 be? If you said the multiplicity for x = -3 is 1, you are correct!!!! Since the exponent on this factor is 1, then its multiplicity is 1. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = -3? If you said it crosses the x-axis at the zero x = -3, pat yourself on the back!!! It does this because the multiplicity is 1, which is odd. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = 3 is a zero What would the multiplicity of the zero x = 3 be? If you said the multiplicity for x = 3 is 1, you are correct!!!! Since the exponent on this factor is 1, then its multiplicity is 1. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = 3? If you said it crosses the x-axis at the zero x = 3, pat yourself on the back!!! It does this because the multiplicity is 1, which is odd. Graphing a Polynomial Function Step 1: Determine the graph’s end behavior.
Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Step 2: Find the x-intercepts or zeros of the function. Recall that you find your x-intercept or zero by setting your function equal to 0, f(x) = 0, completely factoring the polynomial and setting each factor equal to 0. If you need a review on x-intercepts, feel free to go to Tutorial 26: Equations of Lines. Keep in mind that when is a factor of your polynomial and a) if k is even, the graph touches the x-axis at r and turns around. b) if k is odd, the graph crosses the x-axis at r. Step 3: Find the y-intercept of the function. Recall that you can find your y-intercept by letting x = 0 and find your functional value at x = 0, f(0). If you need a review on y-intercepts, feel free to go to Tutorial 26: Equations of Lines. Step 4: Determine if there is any symmetry. y-axis symmetry: Recall that your function is symmetric about the y-axis if it is an even function. In other words, if f(-x) = f(x), then your function is symmetric about the y-axis.
Origin symmetry: Recall that your function is symmetric about the origin if it is an odd function. In other words, if f(-x) = -f(x), then your function is symmetric about the origin. If you need a review on even and odd functions, feel free to go to Tutorial 32: Graphs of Functions, Part II. Step 5: Find the number of maximum turning points. As discussed above, if f is a polynomial function of degree n, then there is at most n - 1 turning points on the graph off. Step 6: Find extra points, if needed. Sometimes you may need to find points that are in between the ones you found in steps 2 and 3 to help you be more accurate on your graph. Step 7: Draw the graph. Plot the points found in steps 2, 3, and 6 and use the information gathered in steps 1, 2, 4, and 5 to draw your graph. The graph of polynomial functions is always a smooth continuous curve. Example 7: Given the polynomial function a) use the Leading Coefficient Test to determine the graph’s end behavior, b) find the x- intercepts (or zeros) and state whether the graph crosses the x-axis or touches the x-axis and turns around at each x-intercept, c) find the y-intercept, d) determine the symmetry of the graph, e) indicate the maximum possible turning points, and f) graph.
Step 1: Determine the graph’s end behavior. Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Do you think that the graph rises or falls to the left and to the right? Since the degree of the polynomial, 4, is even and the leading coefficient, 1, is positive, then the graph of the given polynomial rises to the left and rises to the right. Step 2: Find the x-intercepts or zeros of the function. *Factor out a GCF *Factor a trinomial First Factor: *Setting the 1st factor = 0 *Solve for x *x = 0 is a zero Since the exponent on this factor is 2, then the multiplicity for the zero x = 0 is 2. Since the multiplicity is 2, which is even, then the graph touches the x-axis and turns around at the zero x = 0.
Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = 3 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = 3 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 3. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = -1 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = -1 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = -1. Step 3: Find the y-intercept of the function. Letting x = 0 we get: *Plug in 0 for x
The y-intercept is (0, 0). Step 4: Determine if there is any symmetry. y-axis symmetry: *Plug in -x for x It is not symmetric about the y-axis. Origin symmetry: *Plug in -x for x *Take the opposite of f(x) It is not symmetric about the origin.
Step 5: Find the number of maximum turning points. Since the degree of the function is 4, then there is at most 4 - 1 = 3 turning points. Step 6: Find extra points, if needed. To get a more accurate curve, lets find some points that are in between the points we found in steps 2 and 3: x (x, y) -.5 (-.5, -.437) 1 (1, -4) 2 (2, -12) Step 7: Draw the graph.
Example 8: Given the polynomial function a) use the Leading Coefficient Test to determine the graph’s end behavior, b) find the x-intercepts (or zeros) and state whether the graph crosses the x-axis or touches the x-axis and turns around at each x-intercept, c) find the y-intercept, d) determine the symmetry of the graph, e) indicate the maximum possible turning points, and f) graph. Step 1: Determine the graph’s end behavior. Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Do you think that the graph rises or falls to the left and to the right? Since the degree of the polynomial, 3, is odd and the leading coefficient, -2, is negative, then the graph of the given polynomial rises to the left and falls to the right. Step 2: Find the x-intercepts or zeros of the function. *Factor out a GCF *Factor a diff. of squares First Factor: *Setting the 1st factor = 0 *Solve for x
*x = 0 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = 0 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 0. Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = -1 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = - 1 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = -1. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = 1 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = 1 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 1. Step 3: Find the y-intercept of the function.
Letting x = 0 we get: *Plug in 0 for x The y-intercept is (0, 0). Step 4: Determine if there is any symmetry. y-axis symmetry: *Plug in -x for x It is not symmetric about the y-axis. Origin symmetry:
*Plug in -x for x *Take the opposite of f(x) It is symmetric about the origin. Step 5: Find the number of maximum turning points. Since the degree of the function is 3, then there is at most 3 - 1 = 2 turning points. Step 6: Find extra points, if needed. To get a more accurate curve, lets find some points that are in between the points we found in steps 2 and 3: x (x, y) -1/2 (-1/2, -3/4) 1/2 (1/2, 3/4) Step 7: Draw the graph.
Practice Problems These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer. Practice Problems 1a - 1b: Given the polynomial function a) use the Leading Coefficient Test to determine the graph’s end behavior, b) find the x- intercepts (or zeros) and state whether the graph crosses the x-axis or touches the x-axis and turns around at each x-intercept, c) find the y-intercept, d)
determine the symmetry of the graph, e) indicate the maximum possible turning points, and f) graph. 1a. 1b. (answer/discussion to 1b) (answer/discussion to 1a)

More Related Content

PPT
Polynomial functions
byJessica Garcia
 
PPTX
Division Of Polynomials
byMid Michigan Community College
 
PPTX
Math 8 - Linear Inequalities in Two Variables
byCarlo Luna
 
PPTX
Polynomial function
byDepartment of Education
 
PDF
Probability of Simple and Compound Events
byJoey Fontanilla Valdriz
 
PPT
Remainder theorem
byDepartment of Education
 
DOCX
Factoring Non-Perfect Square Trinomial Lesson Plan
byLorie Jane Letada
 
PPT
Polynomial functionsandgraphs
byJerlyn Fernandez
 
Polynomial functions
byJessica Garcia
 
Division Of Polynomials
byMid Michigan Community College
 
Math 8 - Linear Inequalities in Two Variables
byCarlo Luna
 
Polynomial function
byDepartment of Education
 
Probability of Simple and Compound Events
byJoey Fontanilla Valdriz
 
Remainder theorem
byDepartment of Education
 
Factoring Non-Perfect Square Trinomial Lesson Plan
byLorie Jane Letada
 
Polynomial functionsandgraphs
byJerlyn Fernandez
 

What's hot

PPTX
Probability of Union of Two events
byJAYHARYLPESALBON1
 
PPT
Rational Exponents
byPhil Saraspe
 
PPTX
Inscribed Angle and Intercepted Arc
bycarren yarcia
 
PDF
General Mathematics - Rational Functions
byJuan Miguel Palero
 
PPT
Factor theorem
byAng Choon Cheng
 
PDF
Union and intersection of events (math 10)
byDamone Odrale
 
PPTX
Midpoint Formula
byGRACEALTO1
 
PPTX
Factoring the greatest common monomial factor
byNara Cocarelli
 
PPTX
ANgle Relationship.pptx
byJeraldelEncepto
 
PPTX
Chapter 2 understanding the normal curve distribution
byAntonio F. Balatar Jr.
 
PDF
3.4 Composition of Functions
bysmiller5
 
PPTX
PROBABILITY OF MUTUALLY EXCLUSIVE EVENTS final.pptx
byReinabelleMarfilMarq
 
PPTX
Factoring Perfect Square Trinomial - SIM
byshie5147
 
PPT
union and intersection of events.ppt
byIzah Catli
 
PPTX
Graphs of polynomial functions
byCarlos Erepol
 
PPT
G10 Math Q3- Week 9- Mutually Exclusive Events.ppt
byCheJavier
 
PPTX
Sim(mathematics 10 polynomial functions)
byileen menes
 
PPTX
Quadratic Function.pptx
byErickConcepcion9
 
PPTX
Product of a binomial and a trinomial involving
byMartinGeraldine
 
PPTX
If and then statements
byValDarylAnhao2
 
Probability of Union of Two events
byJAYHARYLPESALBON1
 
Rational Exponents
byPhil Saraspe
 
Inscribed Angle and Intercepted Arc
bycarren yarcia
 
General Mathematics - Rational Functions
byJuan Miguel Palero
 
Factor theorem
byAng Choon Cheng
 
Union and intersection of events (math 10)
byDamone Odrale
 
Midpoint Formula
byGRACEALTO1
 
Factoring the greatest common monomial factor
byNara Cocarelli
 
ANgle Relationship.pptx
byJeraldelEncepto
 
Chapter 2 understanding the normal curve distribution
byAntonio F. Balatar Jr.
 
3.4 Composition of Functions
bysmiller5
 
PROBABILITY OF MUTUALLY EXCLUSIVE EVENTS final.pptx
byReinabelleMarfilMarq
 
Factoring Perfect Square Trinomial - SIM
byshie5147
 
union and intersection of events.ppt
byIzah Catli
 
Graphs of polynomial functions
byCarlos Erepol
 
G10 Math Q3- Week 9- Mutually Exclusive Events.ppt
byCheJavier
 
Sim(mathematics 10 polynomial functions)
byileen menes
 
Quadratic Function.pptx
byErickConcepcion9
 
Product of a binomial and a trinomial involving
byMartinGeraldine
 
If and then statements
byValDarylAnhao2
 

Similar to Graph of polynomial function

PDF
Polynomials lecture
byAdnanBukhari13
 
PPT
Chapter 2_3 Polynomial Functions and Their Graphs _Blitzer 2_ _1_.ppt
byzijunleong
 
PPTX
Chapter 2_3 Polynomial Functions and Their Graphs _Blitzer 2_ _1_.pptx
byMatmarlluanSolarTori
 
PPT
6.3 evaluating-and-graphing-polynomila-functions
bymorrobea
 
PPT
6.3 evaluating-and-graphing-polynomila-functions
bymorrobea
 
PPTX
TURNING POINTS AND THE END BEHAVIOR OF POLYNOMIAL FUNCTIONS.pptx
byCunananKianneJoy
 
PPT
Lecture 8 section 3.2 polynomial equations
bynjit-ronbrown
 
PPTX
PPT-Graph-of-Polynomial-Function - a Grade 10 Mathematics lesson.pptx
byMARIVICCACAL
 
PPTX
Alg2 lesson 7-1
byCarol Defreese
 
PPTX
G10 Math Q2 Week 1- Graph of Polynomial Functions.pptx
bymerwinsonmanzano4
 
PDF
5.2 Power Functions and Polynomial Functions
bysmiller5
 
PPTX
G10 Math Q2 Week 1- Graph of Polynomial Functions.pptx
byJennyRoseAguila
 
PPTX
Alg2 lesson 7-1
byCarol Defreese
 
PPTX
Mathematics 10 Graphs of Polynomial Functions.pptx
byshahanieabbat3
 
PDF
end behavior.....pdf
byLunaLedezma3
 
PDF
New day 5 examples
byjchartiersjsd
 
PPTX
end behavior.....pptx
byLunaLedezma3
 
PDF
Day 5 examples u5w14
byjchartiersjsd
 
PPT
grph_of_polynomial_fnctn.ppt
byLunaLedezma3
 
DOCX
Polynomial functions modelllings
byTarun Gehlot
 
Polynomials lecture
byAdnanBukhari13
 
Chapter 2_3 Polynomial Functions and Their Graphs _Blitzer 2_ _1_.ppt
byzijunleong
 
Chapter 2_3 Polynomial Functions and Their Graphs _Blitzer 2_ _1_.pptx
byMatmarlluanSolarTori
 
6.3 evaluating-and-graphing-polynomila-functions
bymorrobea
 
6.3 evaluating-and-graphing-polynomila-functions
bymorrobea
 
TURNING POINTS AND THE END BEHAVIOR OF POLYNOMIAL FUNCTIONS.pptx
byCunananKianneJoy
 
Lecture 8 section 3.2 polynomial equations
bynjit-ronbrown
 
PPT-Graph-of-Polynomial-Function - a Grade 10 Mathematics lesson.pptx
byMARIVICCACAL
 
Alg2 lesson 7-1
byCarol Defreese
 
G10 Math Q2 Week 1- Graph of Polynomial Functions.pptx
bymerwinsonmanzano4
 
5.2 Power Functions and Polynomial Functions
bysmiller5
 
G10 Math Q2 Week 1- Graph of Polynomial Functions.pptx
byJennyRoseAguila
 
Alg2 lesson 7-1
byCarol Defreese
 
Mathematics 10 Graphs of Polynomial Functions.pptx
byshahanieabbat3
 
end behavior.....pdf
byLunaLedezma3
 
New day 5 examples
byjchartiersjsd
 
end behavior.....pptx
byLunaLedezma3
 
Day 5 examples u5w14
byjchartiersjsd
 
grph_of_polynomial_fnctn.ppt
byLunaLedezma3
 
Polynomial functions modelllings
byTarun Gehlot
 

More from Allan Gulinao

DOCX
Geography of Nigeria
byAllan Gulinao
 
PPTX
Educational System
byAllan Gulinao
 
DOC
Egypt Educational System
byAllan Gulinao
 
DOCX
Venezuela Educational System
byAllan Gulinao
 
DOCX
South Korea Educational System
byAllan Gulinao
 
DOC
Malaysia Educational System
byAllan Gulinao
 
DOCX
Libya Educational System
byAllan Gulinao
 
DOCX
Implementing rules and regulations of k to 12
byAllan Gulinao
 
DOC
Canada Educational System
byAllan Gulinao
 
DOCX
Transversal.lines.3rdyr
byAllan Gulinao
 
DOCX
Finland Educational System
byAllan Gulinao
 
DOCX
Lesson plan
byAllan Gulinao
 
Geography of Nigeria
byAllan Gulinao
 
Educational System
byAllan Gulinao
 
Egypt Educational System
byAllan Gulinao
 
Venezuela Educational System
byAllan Gulinao
 
South Korea Educational System
byAllan Gulinao
 
Malaysia Educational System
byAllan Gulinao
 
Libya Educational System
byAllan Gulinao
 
Implementing rules and regulations of k to 12
byAllan Gulinao
 
Canada Educational System
byAllan Gulinao
 
Transversal.lines.3rdyr
byAllan Gulinao
 
Finland Educational System
byAllan Gulinao
 
Lesson plan
byAllan Gulinao
 

Recently uploaded

PPTX
How to Manage Deferred Revenue in Odoo 18 Accounting
byCeline George
 
PPTX
"Aristotle : Father Of Western Philosophy"
bymitalbarathod28
 
PDF
TỔNG HỢP 156 ĐỀ CHÍNH THỨC KỲ THI CHỌN HỌC SINH GIỎI TIẾNG ANH LỚP 12 CÁC TỈN...
byNguyen Thanh Tu Collection
 
PPTX
Reimagining Academic Library Services through Artificial Intelligence: A Case...
byDon Bosco College, Itanagar
 
PDF
Information about the author Shashi Deshpande
bydarshanaparmar6522
 
PPTX
The night at deoli - Ruskin bond's story of first love
byrajibhammar4
 
PPTX
Drug Distribution in Pharmacology: Mechanisms, Barriers, Factors & Volume of ...
byamrin3379
 
PPTX
'Colonial Mentality and Social Identity in Karma by Khushwant Singh'
byKrishnarajsinh Parmar
 
PDF
Types of Foot & Foot Modifications in Birds
byDr. Ramzan Virani
 
PDF
APPSC APPSC AEE-AE GENERAL STUDIES QUESTION PAPER.pdf
byssuser9d8e4e
 
PPTX
" Jaya : Silence as Resistance " - That long silence
bydharabhandari35
 
PPTX
MEMORY &FORGETTING. Shilpa Hotakar.Psychology pptx
bySHILPA HOTAKAR
 
PPTX
West Hatch High School: Year 9 Art Course
byWestHatch
 
PPT
West Hatch High School - GCSE History Option
byWestHatch
 
PDF
Sharad Bisen_Soil Sterilization_Objectives_ICAR Course, Sixth Dean Committee.pdf
bybisensharad
 
PDF
Unit Plan and Unit Test-pdf-Dr. Rajashekhar Shirvalkar, Principal, SMRS B.Ed ...
byRajashekhar Shirvalkar
 
PPTX
West Hatch High School - GCSE Spanish Presentation
byWestHatch
 
PDF
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
PPTX
West Hatch High School - GCSE Media Studies
byWestHatch
 
PPTX
West Hatch High School -- GCSE Geography
byWestHatch
 
How to Manage Deferred Revenue in Odoo 18 Accounting
byCeline George
 
"Aristotle : Father Of Western Philosophy"
bymitalbarathod28
 
TỔNG HỢP 156 ĐỀ CHÍNH THỨC KỲ THI CHỌN HỌC SINH GIỎI TIẾNG ANH LỚP 12 CÁC TỈN...
byNguyen Thanh Tu Collection
 
Reimagining Academic Library Services through Artificial Intelligence: A Case...
byDon Bosco College, Itanagar
 
Information about the author Shashi Deshpande
bydarshanaparmar6522
 
The night at deoli - Ruskin bond's story of first love
byrajibhammar4
 
Drug Distribution in Pharmacology: Mechanisms, Barriers, Factors & Volume of ...
byamrin3379
 
'Colonial Mentality and Social Identity in Karma by Khushwant Singh'
byKrishnarajsinh Parmar
 
Types of Foot & Foot Modifications in Birds
byDr. Ramzan Virani
 
APPSC APPSC AEE-AE GENERAL STUDIES QUESTION PAPER.pdf
byssuser9d8e4e
 
" Jaya : Silence as Resistance " - That long silence
bydharabhandari35
 
MEMORY &FORGETTING. Shilpa Hotakar.Psychology pptx
bySHILPA HOTAKAR
 
West Hatch High School: Year 9 Art Course
byWestHatch
 
West Hatch High School - GCSE History Option
byWestHatch
 
Sharad Bisen_Soil Sterilization_Objectives_ICAR Course, Sixth Dean Committee.pdf
bybisensharad
 
Unit Plan and Unit Test-pdf-Dr. Rajashekhar Shirvalkar, Principal, SMRS B.Ed ...
byRajashekhar Shirvalkar
 
West Hatch High School - GCSE Spanish Presentation
byWestHatch
 
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
West Hatch High School - GCSE Media Studies
byWestHatch
 
West Hatch High School -- GCSE Geography
byWestHatch
 

Graph of polynomial function

  • 1.
    Learning Objectives After completingthis tutorial, you should be able to: 1. Identify a polynomial function. 2. Use the Leading Coefficient Test to find the end behavior of the graph of a given polynomial function. 3. Find the zeros of a polynomial function. 4. Find the multiplicity of a zero and know if the graph crosses the x-axis at the zero or touches the x-axis and turns around at the zero. 5. Know the maximum number of turning points a graph of a polynomial function could have. 6. Graph a polynomial function. Introduction In this tutorial we will be looking at graphs of polynomial functions. If you need a review on functions, feel free to go to Tutorial 30: Introduction to Functions. If you need a review on polynomials in general, feel free to go to Tutorial 6: Polynomials. Basically, the graph of a polynomial function is a smooth continuous curve. There are several main aspects of this type of graph that you can use to help put the curve together. I will be going over how to use the leading term of your polynomial function to determine the end behavior of its graph. We will also be looking at finding the zeros, aka the x-intercepts, as well as the y-intercept of the graph. If you need a review on intercepts, feel free to go to Tutorial 26: Equations of Lines. Another important concept is to know the largest possible number of turning points. This will help you be more accurate in the graph that you draw. That just about covers it. I guess you are ready to get to it.
  • 2.
    Tutorial Polynomial Function A polynomial function is a function that can be written in the form , where are real numbers and n is a nonnegative integer. Basically it is a function whose rule is given by a polynomial in one variable. If you need a review on functions, feel free to go to Tutorial 30: Introduction to Functions. If you need a review on polynomials in general, feel free to go to Tutorial 6: Polynomials. An example of a polynomial function is . Leading Term When the polynomial function is written in standard form, , the leading term is .
  • 3.
    In other words,the leading term is the term that the variable has its highest exponent. The leading term of the function would be . Leading Coefficient When the polynomial function is written in standard form, , the leading coefficient is . Basically, the leading coefficient is the coefficient on the leading term. The leading coefficient of the function would be - 4. Degree of a Term of a Polynomial Function The degree of a term of a polynomial function is the exponent on the variable. Degree of a Polynomial Function When the polynomial function is written in standard form,
  • 4.
    , the degree of the polynomial function is n. The degree of the polynomial is the largest degree of all of its terms. The degree of the function would be 7. The Leading Coefficient Test There are four cases that go with this test: Given a polynomial function in standard form : Case 1: If n is odd AND the leading coefficient , is positive, the graph falls to the left andrises to the right: Case 2:
  • 5.
    If n isodd AND the leading coefficient , is negative, the graph rises to the left andfalls to the right. Case 3: If n is even AND the leading coefficient , is positive, the graph rises to the left and to the right. Case 4:
  • 6.
    If n iseven AND the leading coefficient , is negative, the graph falls to the left and to the right. Example 1: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!! Second question is what is the leading term’s degree? If you said 3, you are right on!! 3 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said 5, pat yourself on the back!!
  • 7.
    Putting this informationtogether with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 3, is odd and the leading coefficient, 5, is positive, then the graph of the given polynomial falls to the left and rises to the right. Example 2: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!! Second question is what is the leading term’s degree? If you said 4, you are right on!! 4 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said -1, pat yourself on the back!! Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 4, is even and the leading coefficient, -1, is negative, then the graph of the given polynomial falls to the left and falls to the right.
  • 8.
    Example 3: Usethe Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!! Second question is what is the leading term’s degree? If you said 5, you are right on!! 5 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said -7, pat yourself on the back!! Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 5, is odd and the leading coefficient, -7, is negative, then the graph of the given polynomial rises to the left and falls to the right. Example 4: Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial . First question is what is the leading term? If you said , you are correct!!
  • 9.
    Second question iswhat is the leading term’s degree? If you said 6, you are right on!! 6 is the exponent on the leading term, which also means it is the degree of the polynomial. Third question is what is the coefficient on the leading term? If you said 1, pat yourself on the back!! Putting this information together with the Leading Coefficient Test we can determine the end behavior of the graph of our given polynomial: Since the degree of the polynomial, 6, is even and the leading coefficient, 1, is positive, then the graph of the given polynomial rises to the left and rises to the right. Zeros (or Roots) of Polynomial Functions A zero or root of a polynomial function is the value of x such that f(x) = 0. In other words it is the x-intercept, where the functional value or y is equal to 0. Zero of Multiplicity k If is a factor of a polynomial function f and is not a factor of f, then r is called a
  • 10.
    zero of multiplicity k of f. In other words, when a polynomial function is set equal to zero and has been completely factored and each different factor is written with the highest appropriate exponent, depending on the number of times that factor occurs in the product, the exponent on the factor that the zero is a solution for, gives the multiplicity of that zero. The exponent indicates how many times that factor would be written out in the product, this gives us a multiplicity. Multiplicity of Zeros and the x-intercept There are two cases that go with this concept: Case 1: If r is a zero of even multiplicity: This means the graph touches the x-axis at r and turns around. This happens because the sign of f(x) does not change from one side to the other side of r. Case 2: If r is a zero of odd multiplicity: This means the graph crosses the x-axis at r. This happens because the sign of f(x) changes from one side to the other side of r.
  • 11.
    Turning Points If f is a polynomial function of degree n, then there is at most n - 1 turning points on the graph of f. A turning point is a point at which the graph changes direction. Keep in mind that you can have fewer than n - 1 turning points, but it will never exceed n - 1 turning points. Example 5: Find the zeros for the polynomial function and give the multiplicity for each zero. Indicate whether the graph crosses the x-axis or touches the x-axis and turns around at each zero. First Factor: The first factor is 3, which is a constant. Therefore, there are no zeros that go with this factor. Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = -1/2 is a zero
  • 12.
    What would themultiplicity of the zero x = -1/2 be? If you said the multiplicity for x = -1/2 is 4, you are correct!!!! Since the exponent on this factor is 4, then its multiplicity is 4. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = -1/2? If you said it touches the x-axis and turns around at the zero x = -1/2, pat yourself on the back!!! It does this because the multiplicity is 4, which is even. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = 4 is a zero What would the multiplicity of the zero x = 4 be? If you said the multiplicity for x = 4 is 3, you are correct!!!! Since the exponent on this factor is 3, then its multiplicity is 3. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = 4? If you said it crosses the x-axis at the zero x = 4, pat yourself on the back!!! It does this because the multiplicity is 3, which is odd. Example 6: Find the zeros for the polynomial
  • 13.
    function and give the multiplicity for each zero. Indicate whether the graph crosses the x-axis or touches the x-axis and turns around at each zero. Let’s factor this one first: *Factor out a GCF *Factor a diff. of squares First Factor: *Setting the 1st factor = 0 *Solve for x *x = 0 is a zero What would the multiplicity of the zero x = 0 be? If you said the multiplicity for x = 0 is 2, you are correct!!!! Since the exponent on this factor is 2, then its multiplicity is 2. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = 0? If you said it touches the x-axis and turns around at the zero x = 0, pat yourself on the back!!! It does this because the multiplicity is 2, which is even. Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = -3 is a zero
  • 14.
    What would themultiplicity of the zero x = -3 be? If you said the multiplicity for x = -3 is 1, you are correct!!!! Since the exponent on this factor is 1, then its multiplicity is 1. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = -3? If you said it crosses the x-axis at the zero x = -3, pat yourself on the back!!! It does this because the multiplicity is 1, which is odd. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = 3 is a zero What would the multiplicity of the zero x = 3 be? If you said the multiplicity for x = 3 is 1, you are correct!!!! Since the exponent on this factor is 1, then its multiplicity is 1. Does the graph cross the x-axis or touch the x-axis and turn around at the zero x = 3? If you said it crosses the x-axis at the zero x = 3, pat yourself on the back!!! It does this because the multiplicity is 1, which is odd. Graphing a Polynomial Function Step 1: Determine the graph’s end behavior.
  • 15.
    Use the LeadingCoefficient Test, described above, to find if the graph rises or falls to the left and to the right. Step 2: Find the x-intercepts or zeros of the function. Recall that you find your x-intercept or zero by setting your function equal to 0, f(x) = 0, completely factoring the polynomial and setting each factor equal to 0. If you need a review on x-intercepts, feel free to go to Tutorial 26: Equations of Lines. Keep in mind that when is a factor of your polynomial and a) if k is even, the graph touches the x-axis at r and turns around. b) if k is odd, the graph crosses the x-axis at r. Step 3: Find the y-intercept of the function. Recall that you can find your y-intercept by letting x = 0 and find your functional value at x = 0, f(0). If you need a review on y-intercepts, feel free to go to Tutorial 26: Equations of Lines. Step 4: Determine if there is any symmetry. y-axis symmetry: Recall that your function is symmetric about the y-axis if it is an even function. In other words, if f(-x) = f(x), then your function is symmetric about the y-axis.
  • 16.
    Origin symmetry: Recall that your function is symmetric about the origin if it is an odd function. In other words, if f(-x) = -f(x), then your function is symmetric about the origin. If you need a review on even and odd functions, feel free to go to Tutorial 32: Graphs of Functions, Part II. Step 5: Find the number of maximum turning points. As discussed above, if f is a polynomial function of degree n, then there is at most n - 1 turning points on the graph off. Step 6: Find extra points, if needed. Sometimes you may need to find points that are in between the ones you found in steps 2 and 3 to help you be more accurate on your graph. Step 7: Draw the graph. Plot the points found in steps 2, 3, and 6 and use the information gathered in steps 1, 2, 4, and 5 to draw your graph. The graph of polynomial functions is always a smooth continuous curve. Example 7: Given the polynomial function a) use the Leading Coefficient Test to determine the graph’s end behavior, b) find the x- intercepts (or zeros) and state whether the graph crosses the x-axis or touches the x-axis and turns around at each x-intercept, c) find the y-intercept, d) determine the symmetry of the graph, e) indicate the maximum possible turning points, and f) graph.
  • 17.
    Step 1: Determinethe graph’s end behavior. Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Do you think that the graph rises or falls to the left and to the right? Since the degree of the polynomial, 4, is even and the leading coefficient, 1, is positive, then the graph of the given polynomial rises to the left and rises to the right. Step 2: Find the x-intercepts or zeros of the function. *Factor out a GCF *Factor a trinomial First Factor: *Setting the 1st factor = 0 *Solve for x *x = 0 is a zero Since the exponent on this factor is 2, then the multiplicity for the zero x = 0 is 2. Since the multiplicity is 2, which is even, then the graph touches the x-axis and turns around at the zero x = 0.
  • 18.
    Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = 3 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = 3 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 3. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = -1 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = -1 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = -1. Step 3: Find the y-intercept of the function. Letting x = 0 we get: *Plug in 0 for x
  • 19.
    The y-intercept is(0, 0). Step 4: Determine if there is any symmetry. y-axis symmetry: *Plug in -x for x It is not symmetric about the y-axis. Origin symmetry: *Plug in -x for x *Take the opposite of f(x) It is not symmetric about the origin.
  • 20.
    Step 5: Findthe number of maximum turning points. Since the degree of the function is 4, then there is at most 4 - 1 = 3 turning points. Step 6: Find extra points, if needed. To get a more accurate curve, lets find some points that are in between the points we found in steps 2 and 3: x (x, y) -.5 (-.5, -.437) 1 (1, -4) 2 (2, -12) Step 7: Draw the graph.
  • 21.
    Example 8: Giventhe polynomial function a) use the Leading Coefficient Test to determine the graph’s end behavior, b) find the x-intercepts (or zeros) and state whether the graph crosses the x-axis or touches the x-axis and turns around at each x-intercept, c) find the y-intercept, d) determine the symmetry of the graph, e) indicate the maximum possible turning points, and f) graph. Step 1: Determine the graph’s end behavior. Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Do you think that the graph rises or falls to the left and to the right? Since the degree of the polynomial, 3, is odd and the leading coefficient, -2, is negative, then the graph of the given polynomial rises to the left and falls to the right. Step 2: Find the x-intercepts or zeros of the function. *Factor out a GCF *Factor a diff. of squares First Factor: *Setting the 1st factor = 0 *Solve for x
  • 22.
    *x = 0is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = 0 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 0. Second Factor: *Setting the 2nd factor = 0 *Solve for x *x = -1 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = - 1 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = -1. Third Factor: *Setting the 3rd factor = 0 *Solve for x *x = 1 is a zero Since the exponent on this factor is 1, then the multiplicity for the zero x = 1 is 1. Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 1. Step 3: Find the y-intercept of the function.
  • 23.
    Letting x =0 we get: *Plug in 0 for x The y-intercept is (0, 0). Step 4: Determine if there is any symmetry. y-axis symmetry: *Plug in -x for x It is not symmetric about the y-axis. Origin symmetry:
  • 24.
    *Plug in -xfor x *Take the opposite of f(x) It is symmetric about the origin. Step 5: Find the number of maximum turning points. Since the degree of the function is 3, then there is at most 3 - 1 = 2 turning points. Step 6: Find extra points, if needed. To get a more accurate curve, lets find some points that are in between the points we found in steps 2 and 3: x (x, y) -1/2 (-1/2, -3/4) 1/2 (1/2, 3/4) Step 7: Draw the graph.
  • 25.
    Practice Problems These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer. Practice Problems 1a - 1b: Given the polynomial function a) use the Leading Coefficient Test to determine the graph’s end behavior, b) find the x- intercepts (or zeros) and state whether the graph crosses the x-axis or touches the x-axis and turns around at each x-intercept, c) find the y-intercept, d)
  • 26.
    determine the symmetryof the graph, e) indicate the maximum possible turning points, and f) graph. 1a. 1b. (answer/discussion to 1b) (answer/discussion to 1a)