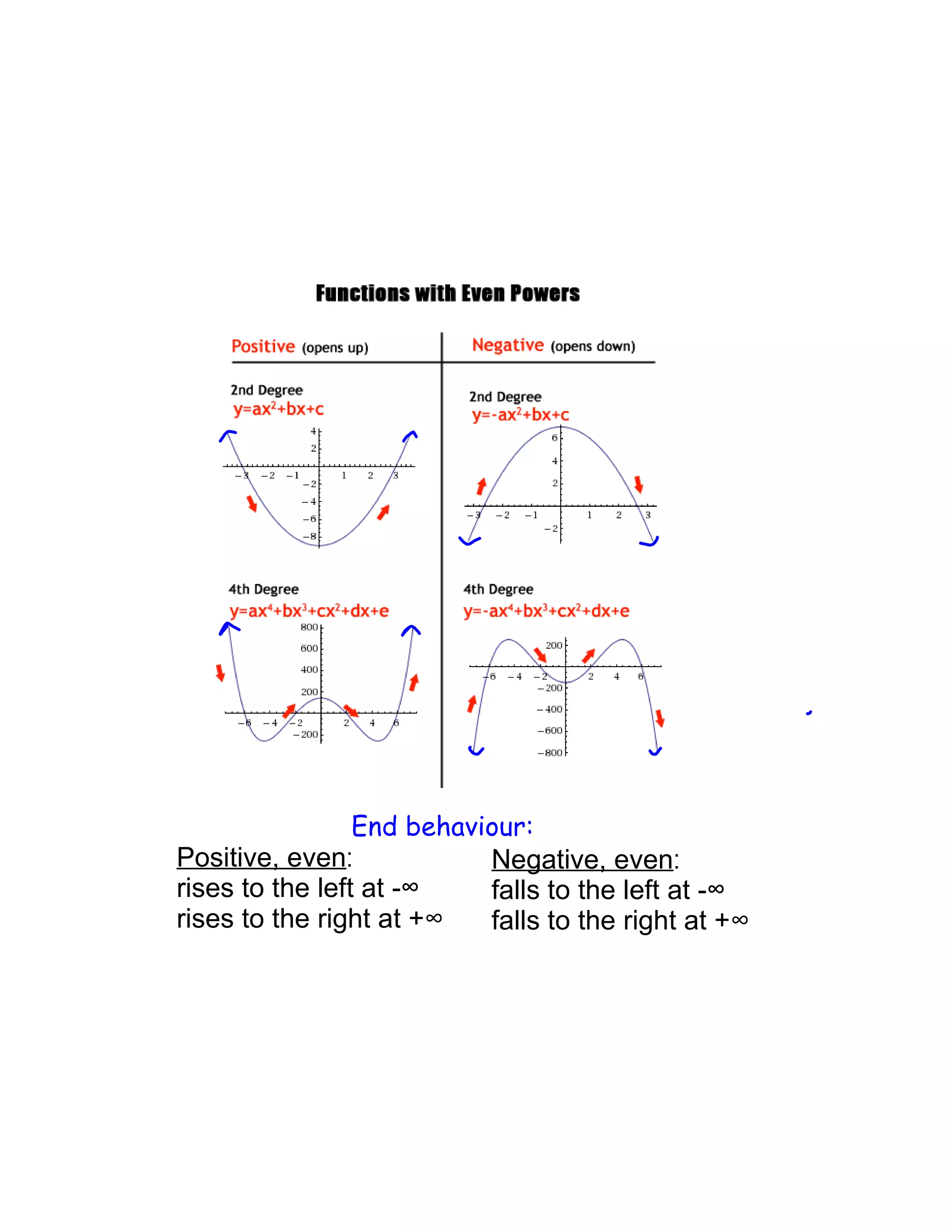
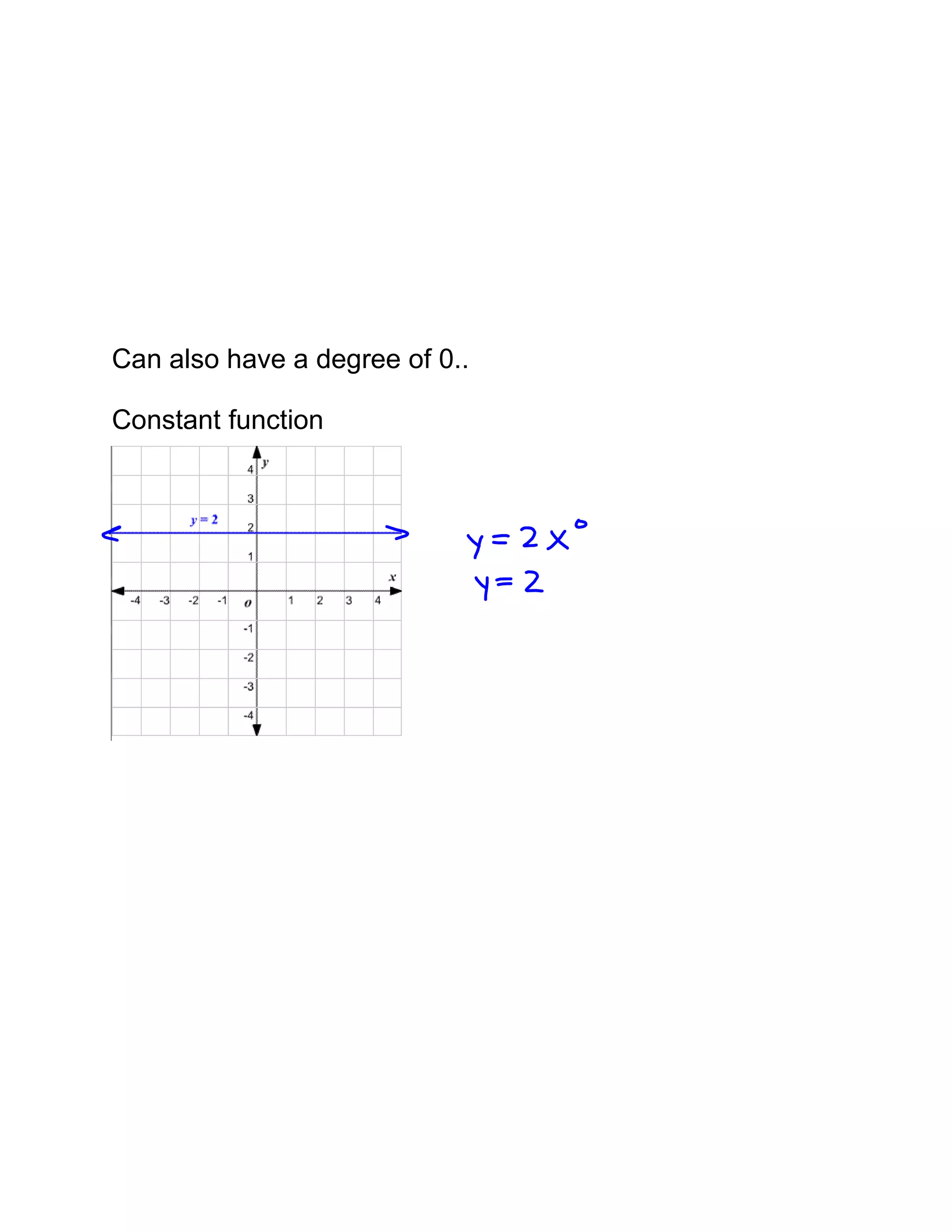
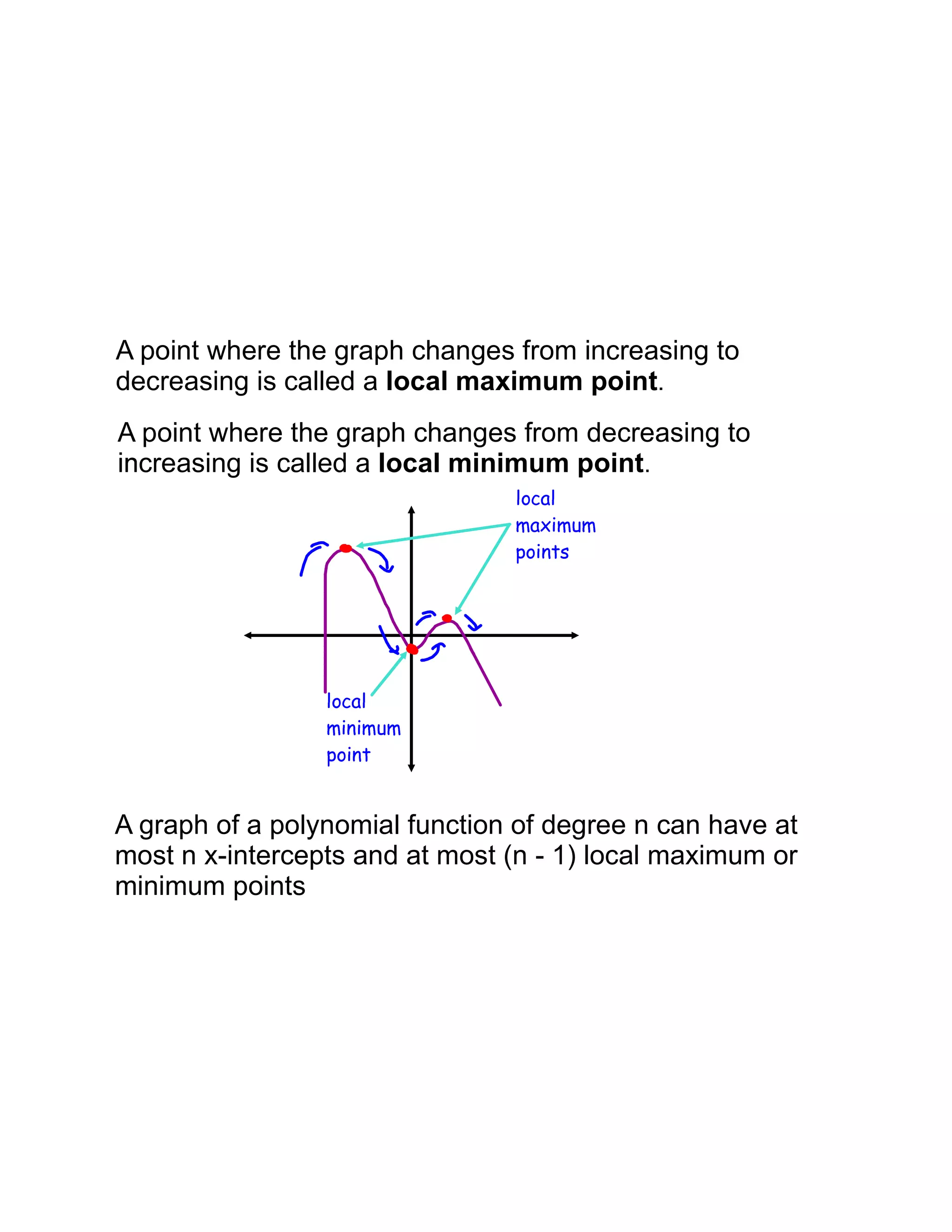
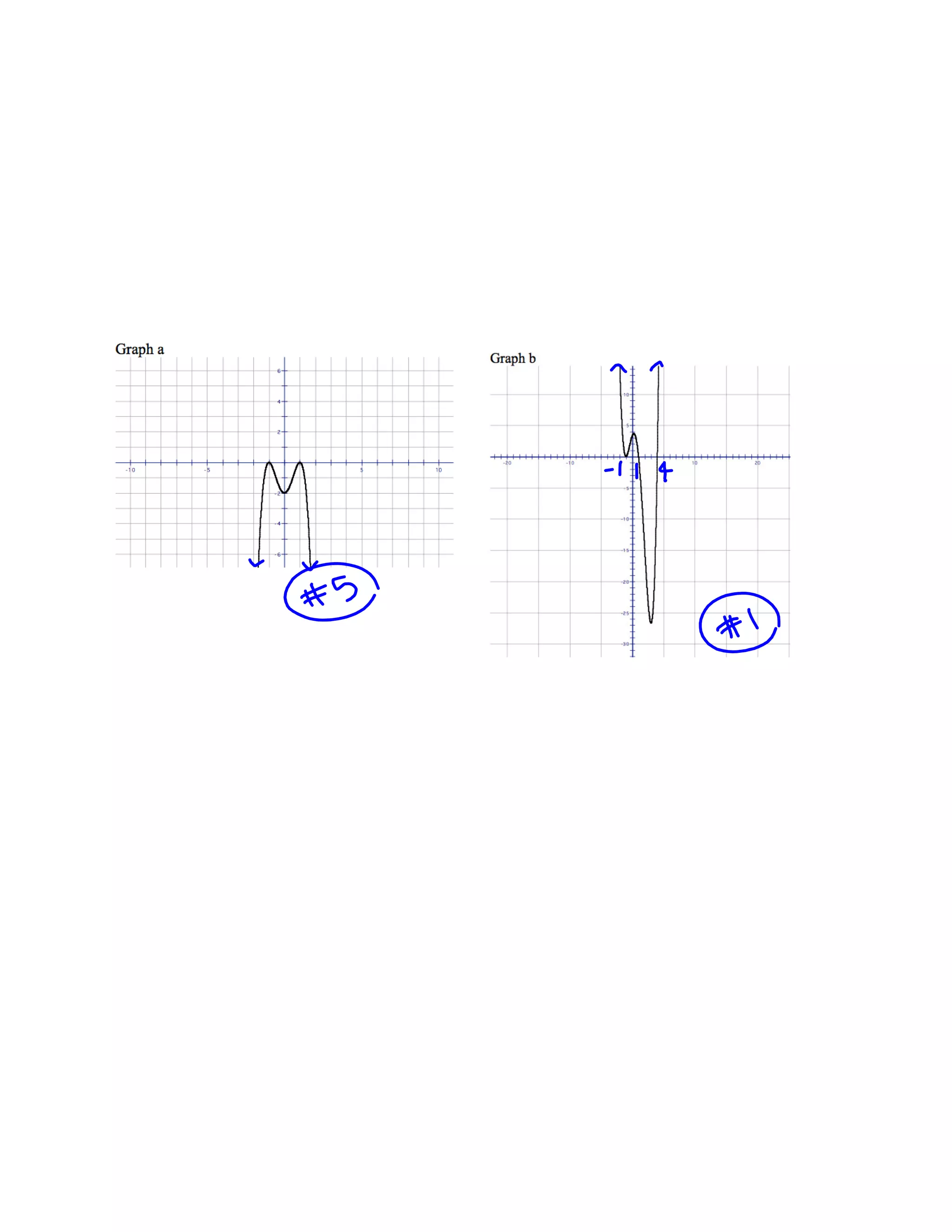
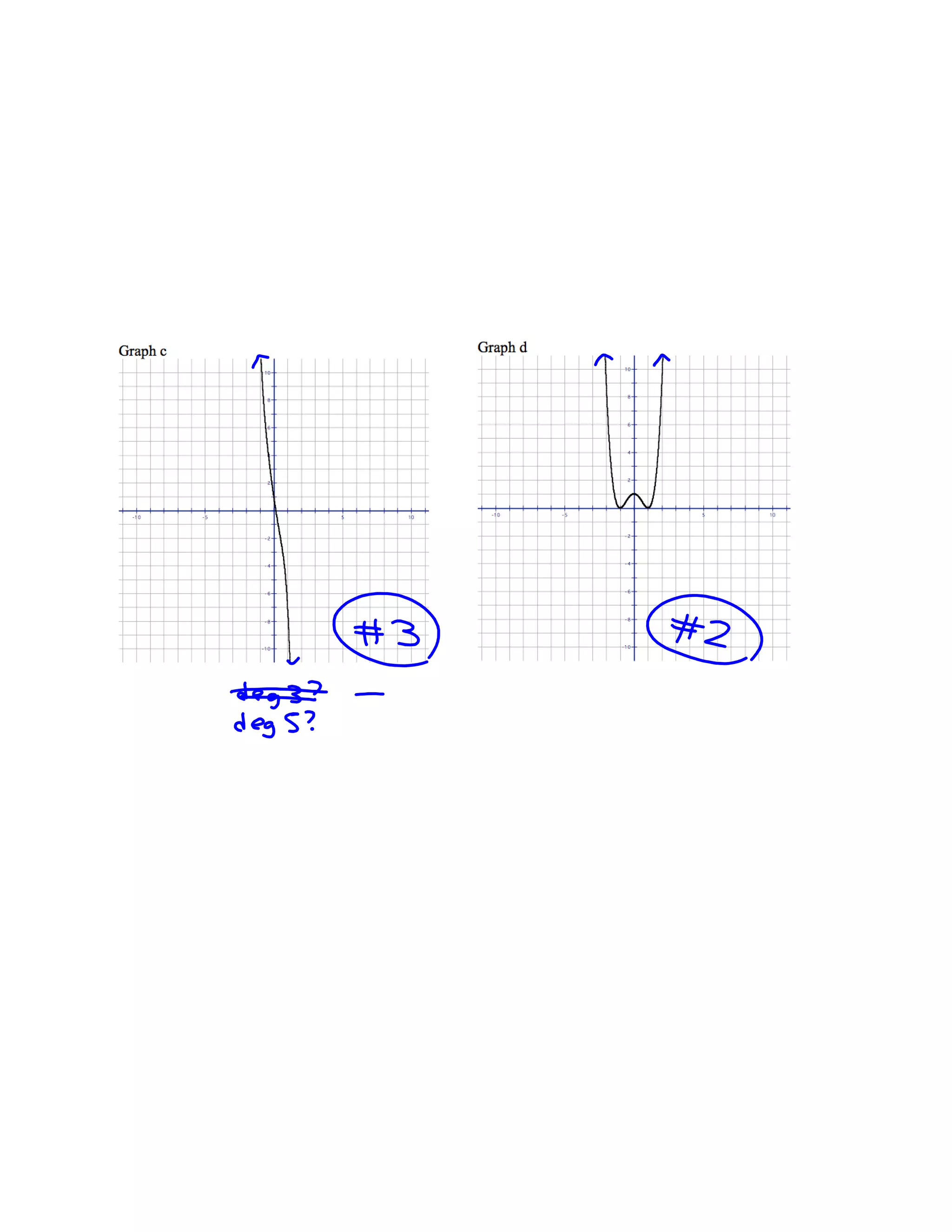
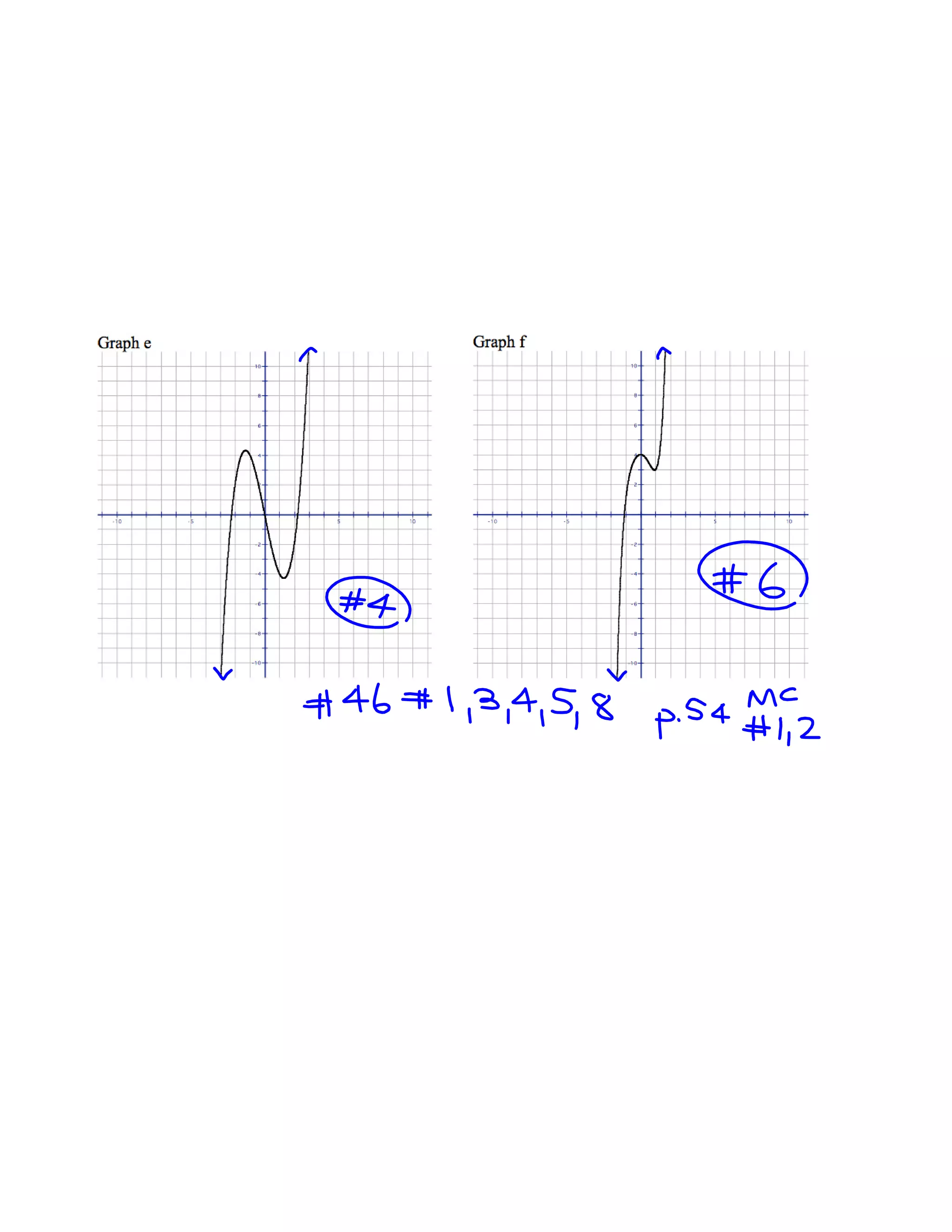
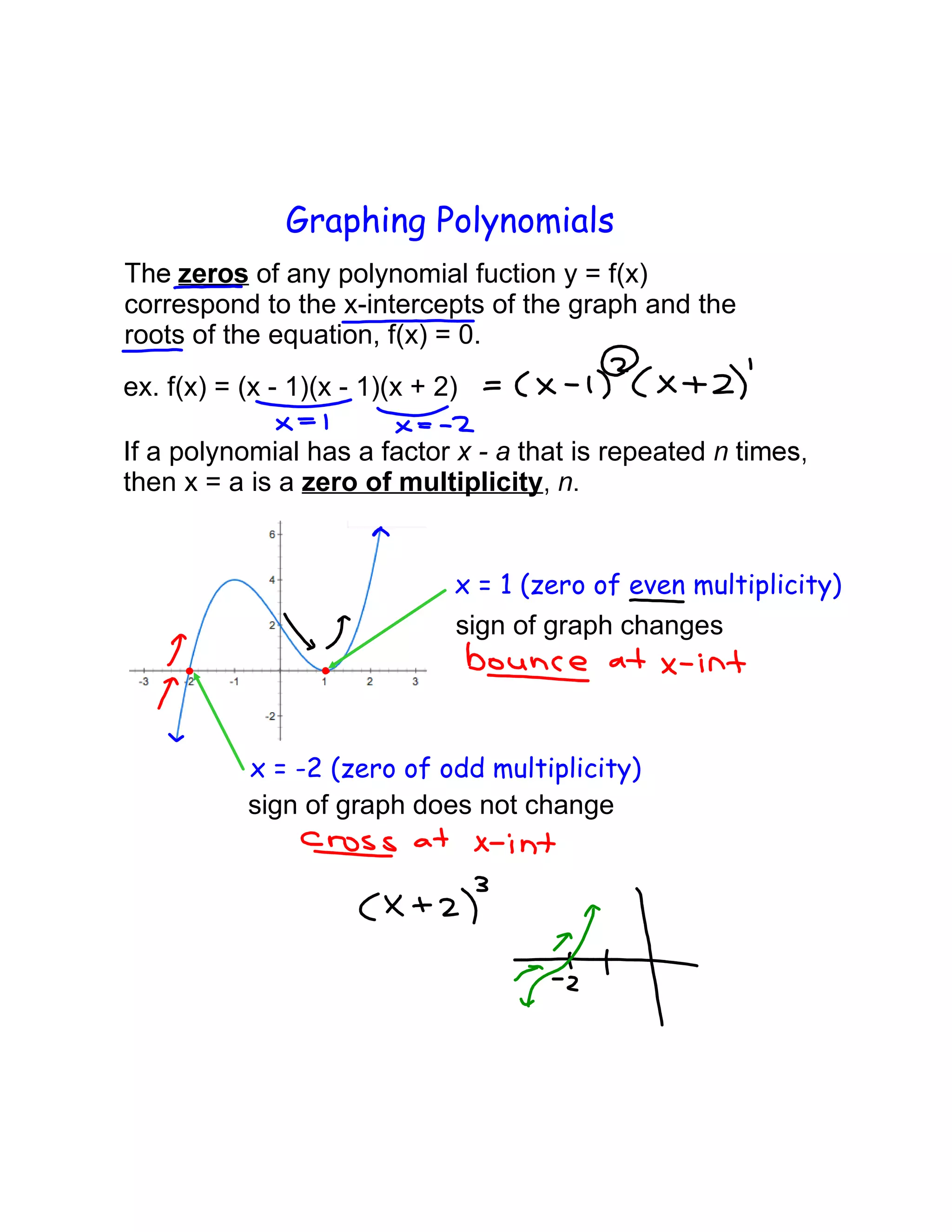
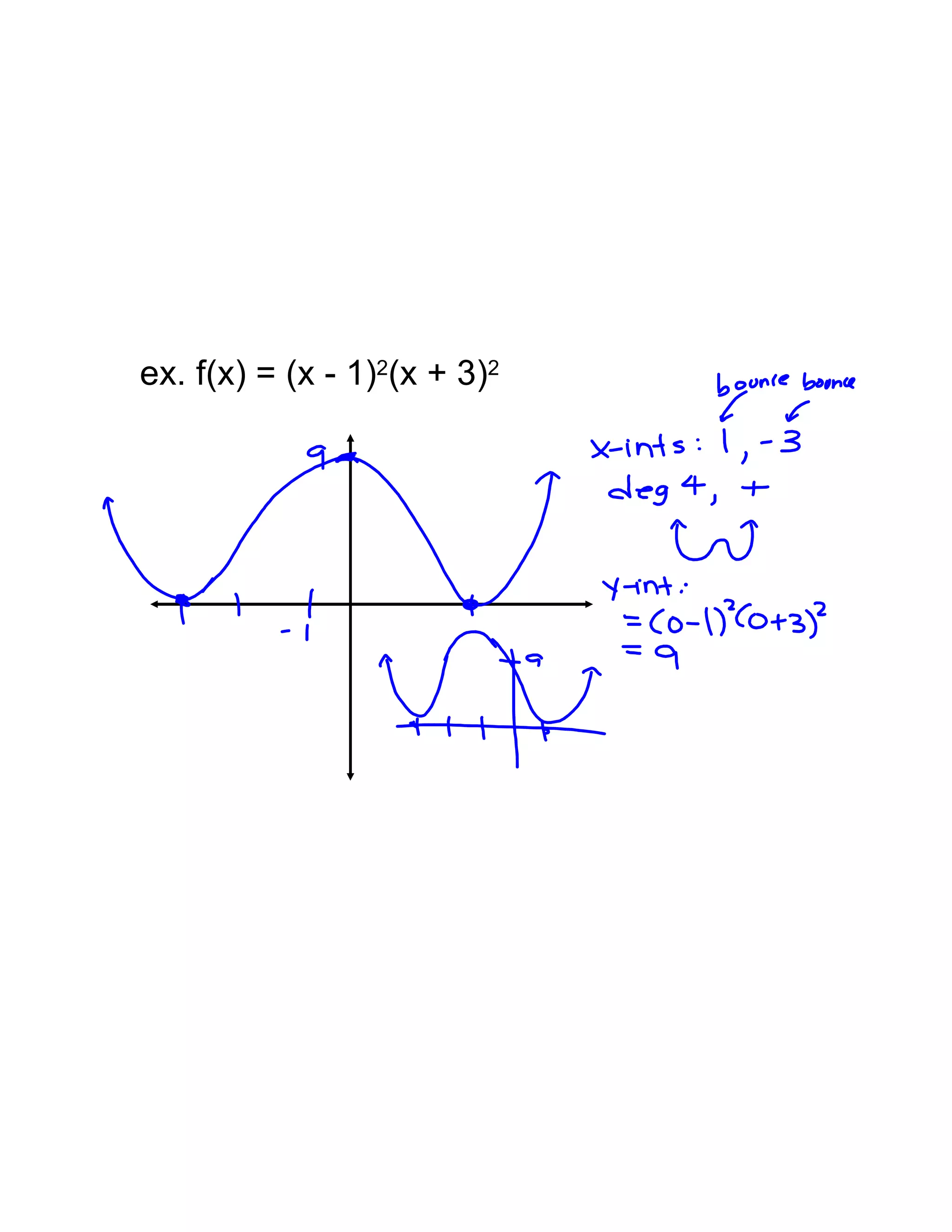
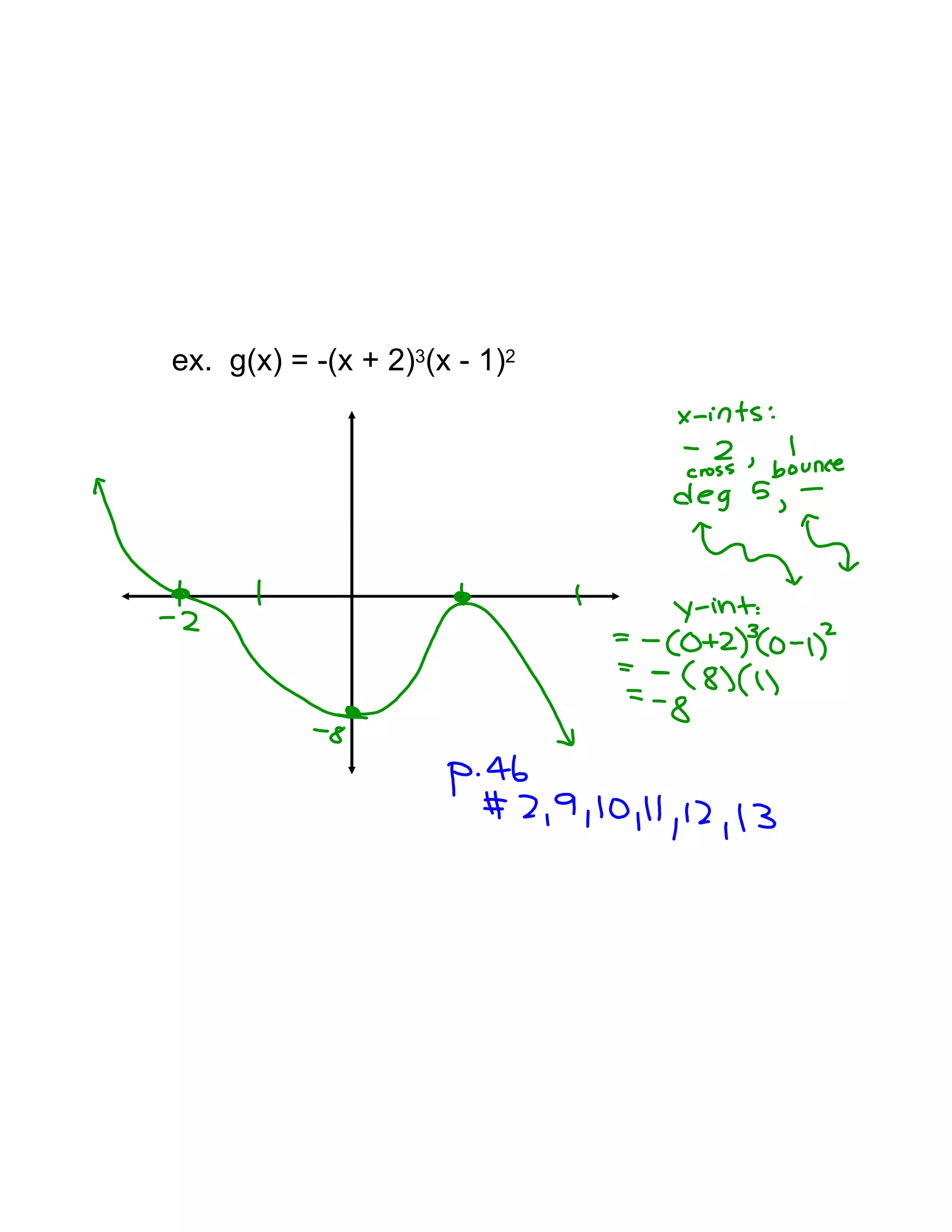
Polynomial functions are described by their degree and have certain characteristics. The graph of a polynomial is smooth and continuous without sharp corners. Odd degree polynomials rise on the left and fall on the right, while even degree polynomials rise on both sides. The number of x-intercepts and local maxima/minima are limited by the degree. Polynomials can be matched based on their degree, leading coefficient, even/odd nature, and number of x-intercepts and local extrema. The x-intercepts of a polynomial correspond to the roots of the equation, and a repeated root indicates a zero of higher multiplicity which affects the graph.

1. Characteristics of Polynomial Functions
Recall, standard form of a polynomial:
+ ... + a
x is a variable
the coefficients a are real numbers
of a polynomial is the highest power of
the variable in the equation.
leading coefficient is the coefficient of the

2. The graph of a polynomial is smooth and continuous
- no sharp corners and can be drawn without lifting a
pencil off a piece of paper
Polynomials can be described by their degree:
- Odd-degree polynomials (1, 3, 5, etc.)
- Even-degree polynomials (2, 4, etc.)
- Linear (degree 1)
- Quadratic (degree 2)
(degree 3)
- Quartic (degree 4)
- Quintic (degree 5)

3. Positive, odd
falls to the left at -
rises to the right at +∞
End behaviour:
Negative, odd
rises to the left at -
falls to the right at +∞

4. Positive, even
rises to the left at -
rises to the right at +∞
End behaviour:
Negative, even
falls to the left at -
falls to the right at +∞

5. Can also have a degree of 0..
Constant function

6. A point where the graph changes from increasing to
decreasing is called a local maximum point
A point where the graph changes from decreasing to
creasing is called a local minimum point
A graph of a polynomial function of degree n can have at
most n x-intercepts and at most (n - 1) local maximum or
minimum points

7. Polynomial Matching
What to look for?
- degree
- leading coefficient
- even or odd
- number of x-intercepts
- number of local max/min
- end behaviour

11. Graphing Polynomials
of any polynomial fuction y = f(x)
correspond to the x-intercepts of the graph and the
roots of the equation, f(x) = 0.
ex. f(x) = (x - 1)(x - 1)(x + 2)
If a polynomial has a factor that is repeated
then x = a is a zero of multiplicity
x = 1 (zero of even multiplicity)
x = -2 (zero of odd multiplicity)
sign of graph changes
sign of graph does not change

12. ex. f(x) = (x - 1)2(x + 3)2

13. ex. g(x) = -(x + 2)3(x - 1)2