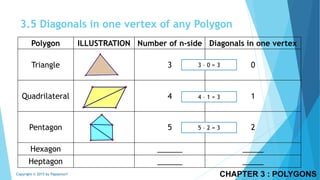
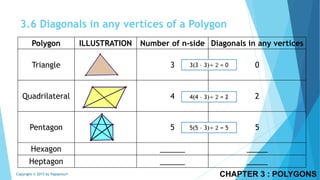
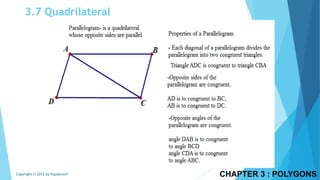
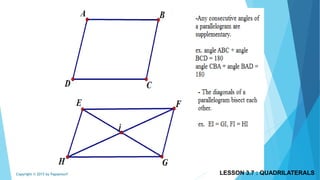
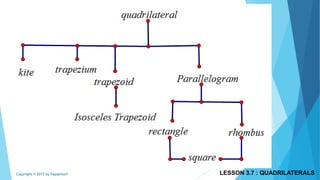
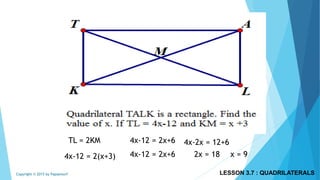
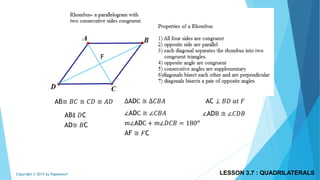
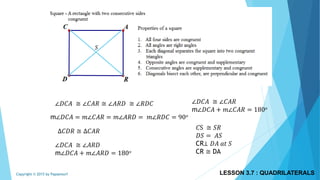
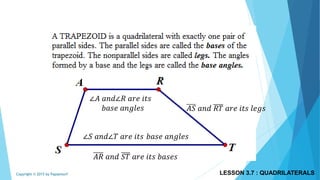
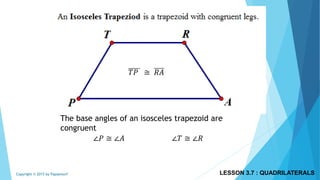
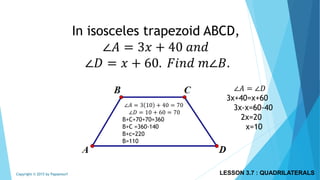
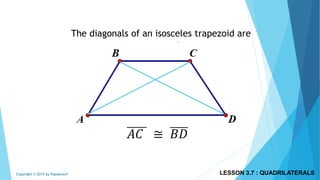
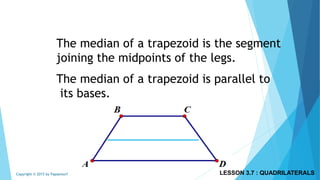
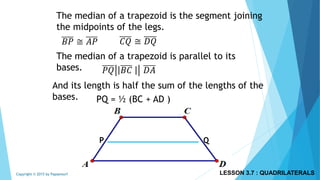
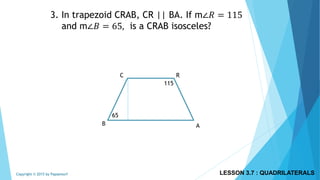
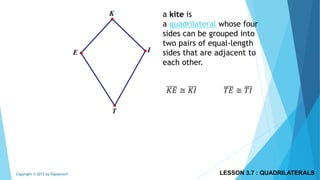
This document discusses different types of polygons and their properties. It begins by defining polygons as closed, planar shapes with three or more sides. It then covers terminology related to polygons such as vertices, sides, and diagonals. Several key properties of polygons are examined, including the sum of interior angles being (n-2)*180 degrees for an n-sided polygon and the sum of exterior angles always being 360 degrees. The document also discusses the number of diagonals that can be drawn in a single vertex or across all vertices of different polygons. Finally, it covers specific types of quadrilaterals like parallelograms, rectangles, squares, rhombi, and trapezoids.