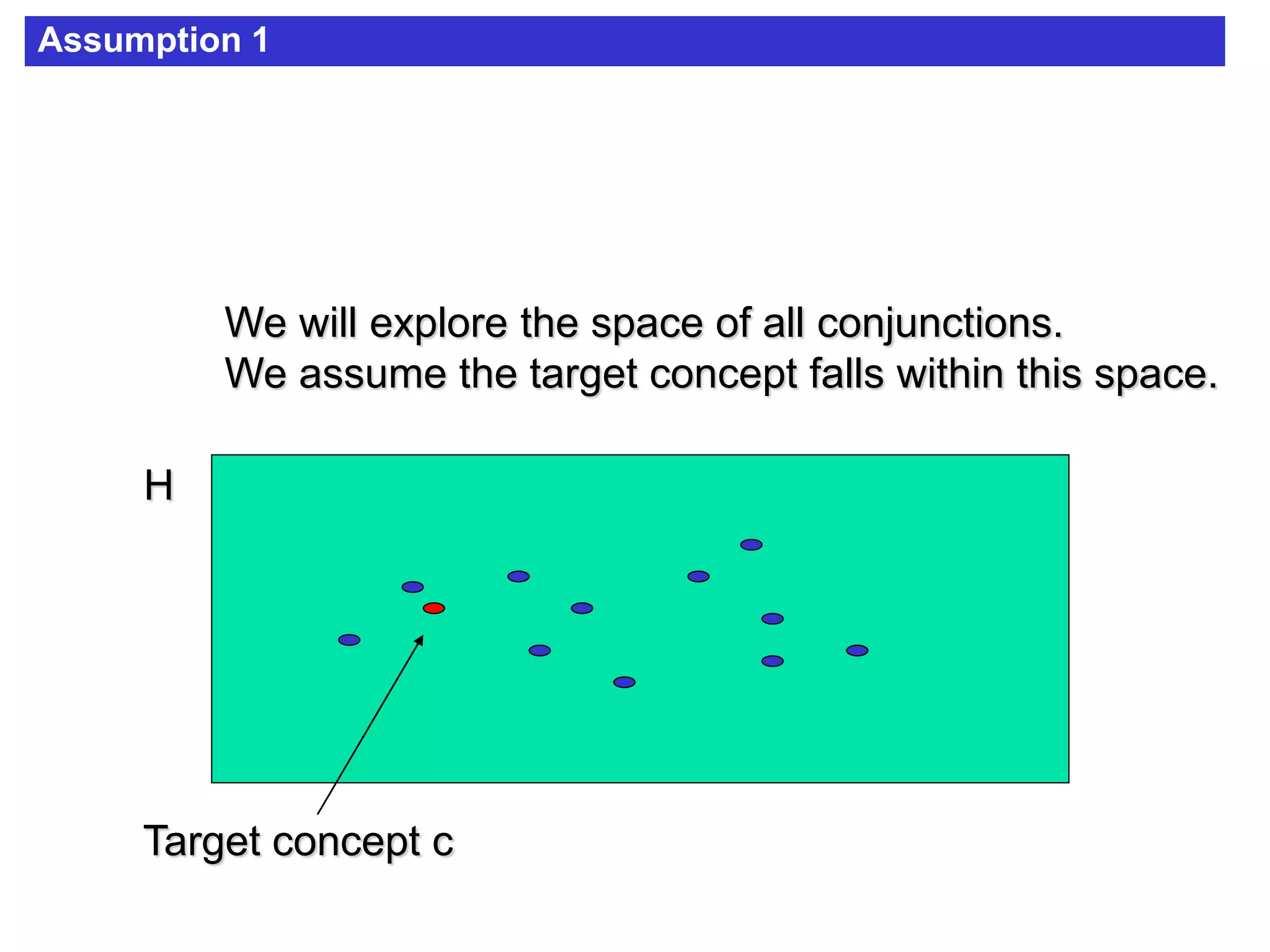
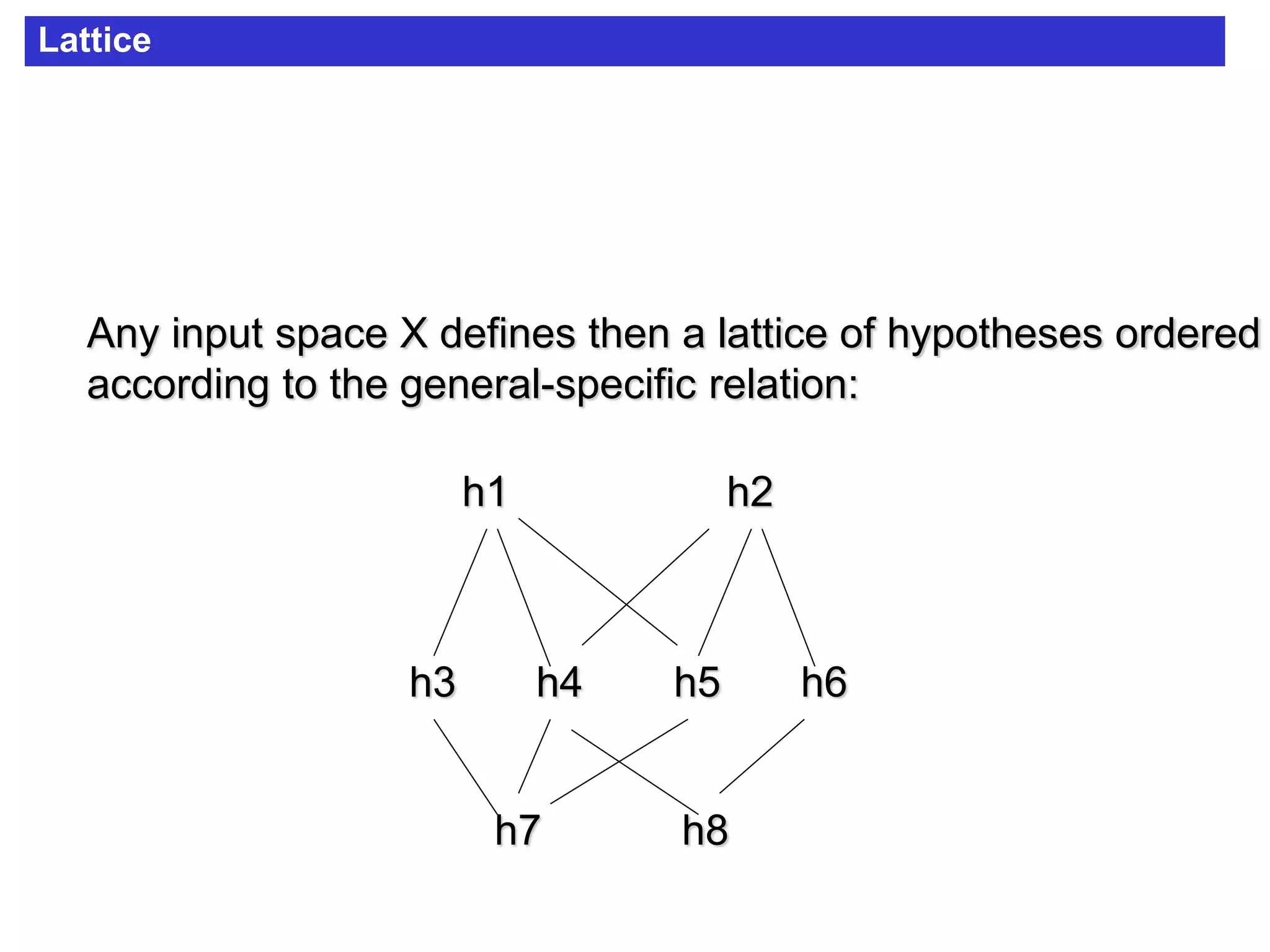
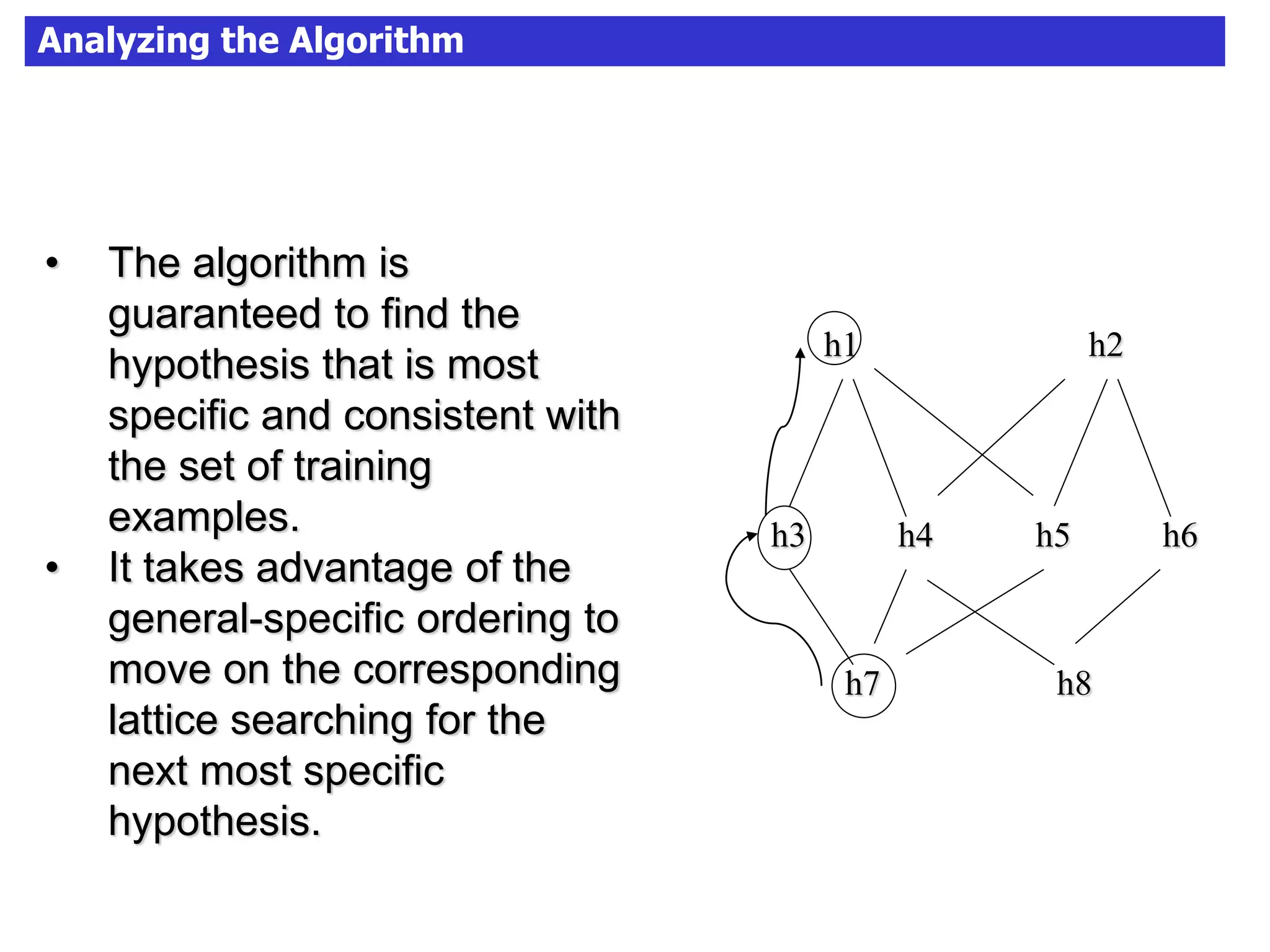
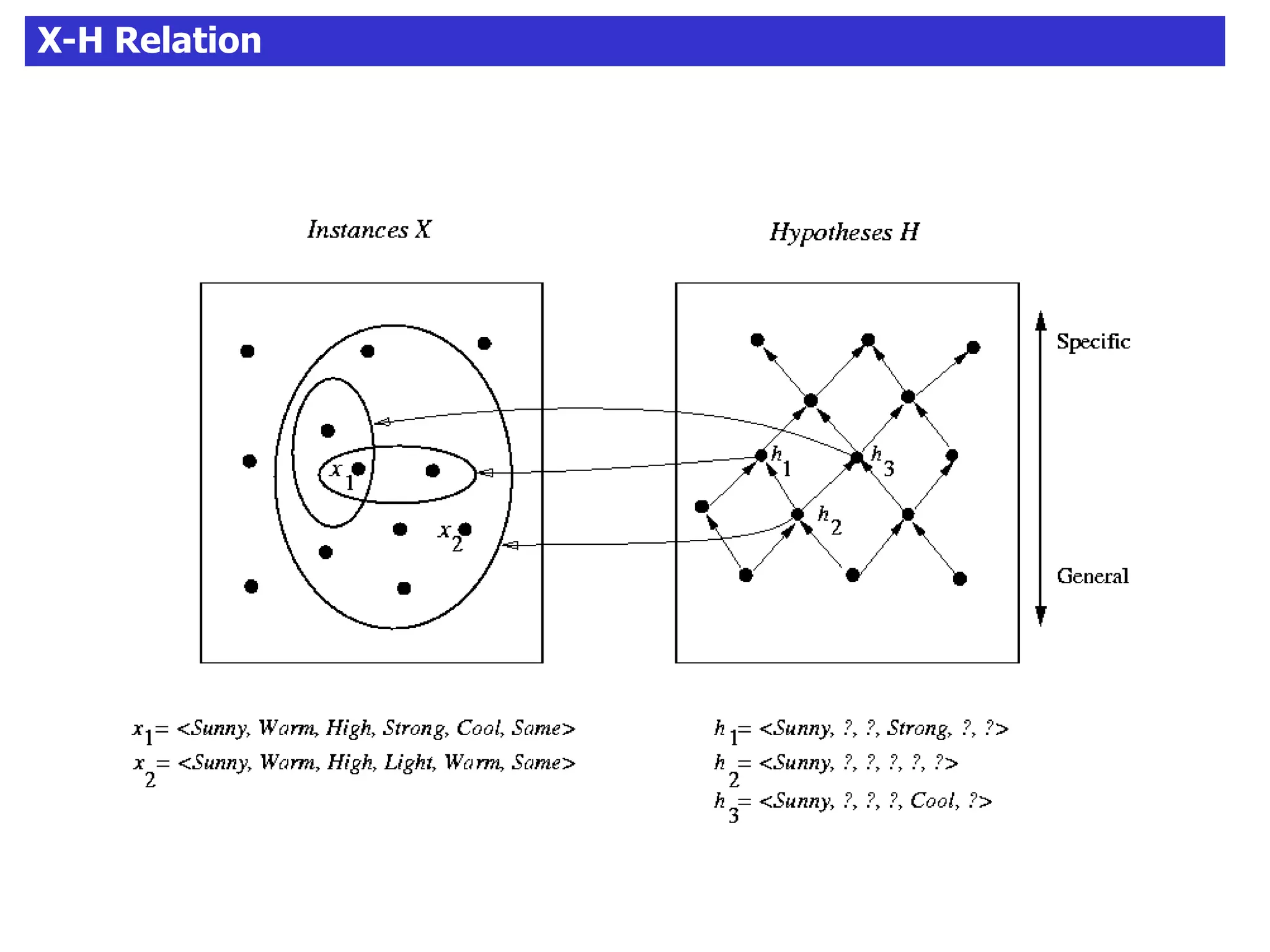
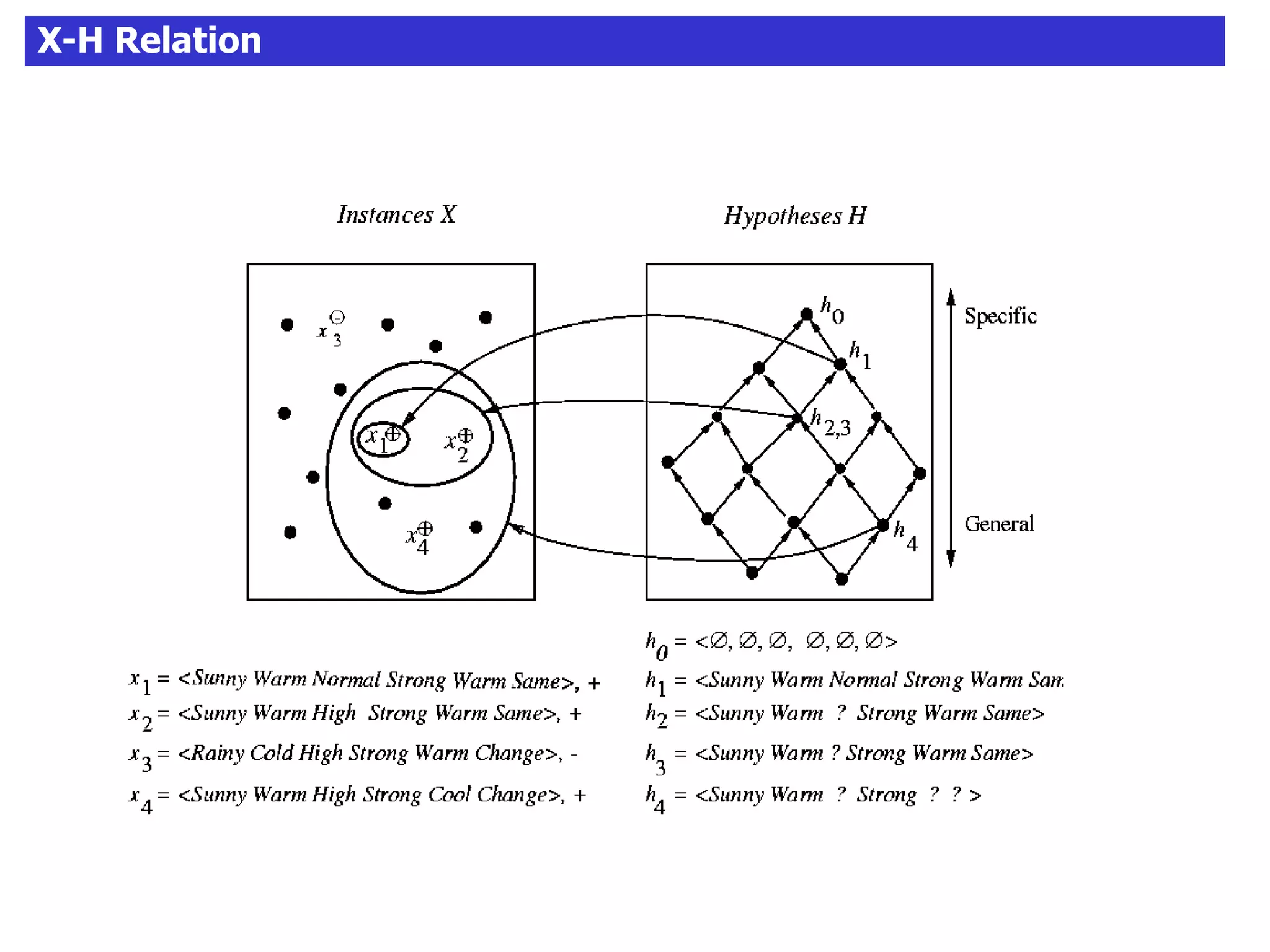
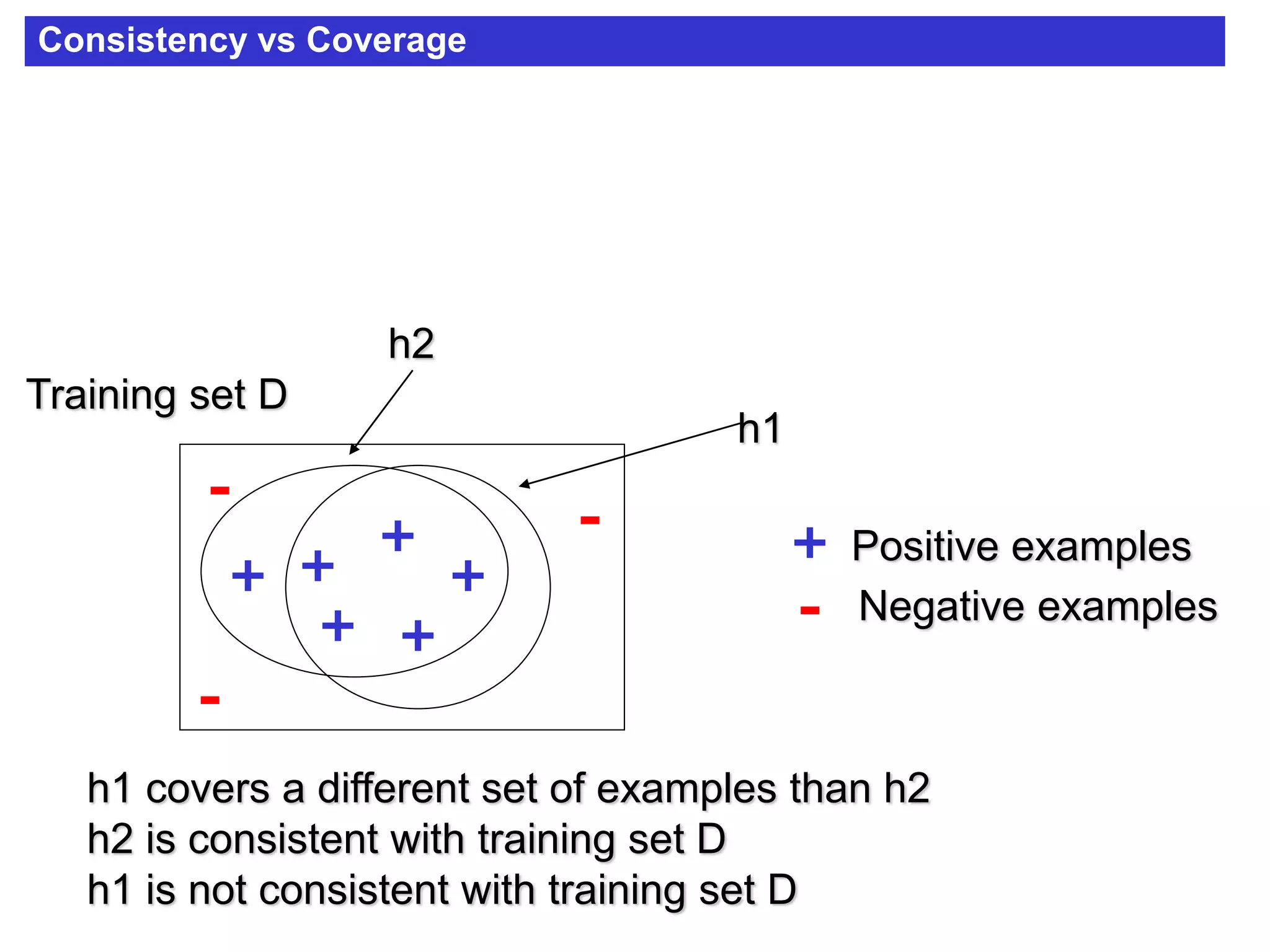
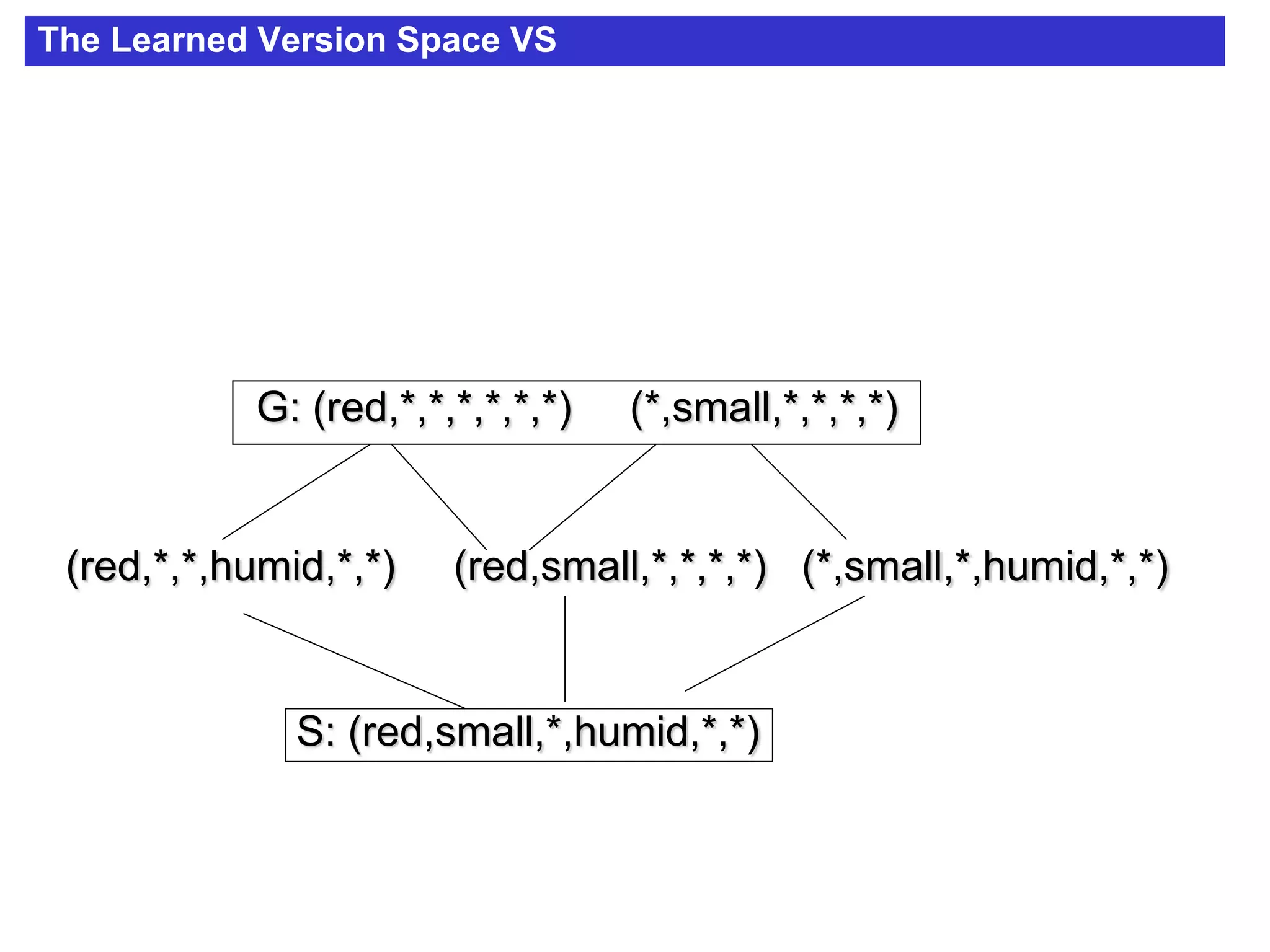
The document discusses concept learning algorithms. It introduces the problem of concept learning as inducing a function to classify examples into categories based on their attributes. The Candidate Elimination Algorithm (CEA) is presented as a method for finding all hypotheses consistent with training examples without enumerating them. CEA works by maintaining the most specific (S) and most general (G) consistent hypotheses. It updates S and G in response to positive and negative examples.

1. Buenos Aires, abril de 2016
Eduardo Poggi
http://www.shutterstock.com/

2. Concept Learning
 Definitions
 Search Space and General-Specific Ordering
 Concept learning as search
 FIND-S
 The Candidate Elimination Algorithm
 Inductive Bias

3. First definition
 The problem is to learn a function mapping examples into two
classes: positive and negative.
 We are given a database of examples already classified as positive or
negative.
 Concept learning: the process of inducing a function mapping input
examples into a Boolean output.

4. Notation
 Set of instances X
 Target concept c : X  {+,-}
 Training examples E = {(x , c(x))}
 Data set D  X
 Set of possible hypotheses H
 h  H / h : X  {+,-}
 Goal: Find h / h(x)=c(x)

5. Representation of Examples
Features:
• color {red, brown, gray}
• size {small, large}
• shape {round,elongated}
• land {humid,dry}
• air humidity {low,high}
• texture {smooth, rough}

6. The Input and Output Space
X
Only a small subset is contained
in our database.
Y = {+,-}
X : The space of all possible examples (input space).
Y: The space of classes (output space).
An example in X is a feature vector X.
For instance: X = (red,small,elongated,humid,low,rough)
X is the cross product of all feature values.

7. The Training Examples
D: The set of training examples.
D is a set of pairs { (x,c(x)) }, where c is the target concept
Example of D:
((red,small,round,humid,low,smooth), +)
((red,small,elongated,humid,low,smooth),+)
((gray,large,elongated,humid,low,rough), -)
((red,small,elongated,humid,high,rough), +)
Instances from the input space
Instances from
the output space

8. Hypothesis Representation
Consider the following hypotheses:
(*,*,*,*,*,*): all mushrooms are poisonous
(0,0,0,0,0,0): no mushroom is poisonous
Special symbols:
 * Any value is acceptable
 0 no value is acceptable
Any hypothesis h is a function from X to Y
h: X Y
We will explore the space of conjunctions.

9. Hypothesis Space
The space of all hypotheses is represented by H
Let h be a hypothesis in H.
Let X be an example of a mushroom.
if h(X) = + then X is poisonous,
otherwise X is not-poisonous
Our goal is to find the hypothesis, h*, that is very “close”
to target concept c.
A hypothesis is said to “cover” those examples it classifies
as positive.
X
h

10. Assumption 1
We will explore the space of all conjunctions.
We assume the target concept falls within this space.
Target concept c
H

11. Assumption 2
A hypothesis close to target concept c obtained after
seeing many training examples will result in high
accuracy on the set of unobserved examples.
Training set D
Hypothesis h* is good
Complement set D’
Hypothesis h* is good

12. Concept Learning as Search
There is a general to specific ordering inherent to any
hypothesis space.
Consider these two hypotheses:
h1 = (red,*,*,humid,*,*)
h2 = (red,*,*,*,*,*)
We say h2 is more general than h1 because h2 classifies
more instances than h1 and h1 is covered by h2.

13. General-Specific
For example, consider the following hypotheses:
h1
h2 h3
h1 is more general than h2 and h3.
h2 and h3 are neither more specific nor more general
than each other.

14. Let hj and hk be two hypotheses mapping examples into {+,-}.
We say hj is more general than hk iff
For all examples X, hk(X) = +  hj(X) = +
We represent this fact as hj >= hk
The >= relation imposes a partial ordering over the
hypothesis space H (reflexive, antisymmetric, and transitive).
Definition

15. Lattice
Any input space X defines then a lattice of hypotheses ordered
according to the general-specific relation:
h1
h3 h4
h2
h5 h6
h7 h8

16. Working Example: Mushrooms
Class of Tasks: Predicting poisonous mushrooms
Performance: Accuracy of Classification
Experience: Database describing mushrooms with their class
Knowledge to learn:
Function mapping mushrooms to {+,-}
where -:not-poisonous and +:poisonous
Representation of target knowledge:
conjunction of attribute values.
Learning mechanism:
Find-S

17. Finding a Maximally-Specific Hypothesis
Algorithm to search the space of conjunctions:
 Start with the most specific hypothesis
 Generalize the hypothesis when it fails to cover a positive
example
Algorithm:
1. Initialize h to the most specific hypothesis
2. For each positive training example X
For each value a in h
If example X and h agree on a, do nothing
else generalize a by the next more general constraint
3. Output hypothesis h

18. Example
Let’s run the learning algorithm above with the
following examples:
((red,small,round,humid,low,smooth), +)
((red,small,elongated,humid,low,smooth),+)
((gray,large,elongated,humid,low,rough), -)
((red,small,elongated,humid,high,rough), +)
We start with the most specific hypothesis:
h = (0,0,0,0,0,0)
The first example comes and since the example is positive and h
fails to cover it, we simply generalize h to cover exactly this
example: h = (red,small,round,humid,low,smooth)

19. Example
Hypothesis h basically says that the first example is the only
positive example, all other examples are negative.
Then comes examples 2:
((red,small,elongated,humid,low,smooth), poisonous)
This example is positive. All attributes match hypothesis h
except for attribute shape: it has the value elongated, not
round.
We generalize this attribute using symbol * yielding:
h: (red,small,*,humid,low,smooth)
The third example is negative and so we just ignore it.
Why is it we don’t need to be concerned with negative
examples?

20. Example
Upon observing the 4th example, hypothesis h is
generalized to the following:
h = (red,small,*,humid,*,*)
h is interpreted as any mushroom that is red, small and
found on humid land should be classified as poisonous.

21. Analyzing the Algorithm
• The algorithm is
guaranteed to find the
hypothesis that is most
specific and consistent with
the set of training
examples.
• It takes advantage of the
general-specific ordering to
move on the corresponding
lattice searching for the
next most specific
hypothesis.
h1
h3 h4
h2
h5 h6
h7 h8

22. X-H Relation

23. X-H Relation

24. Points to Consider
 There are many hypotheses consistent with the training data D.
 Why should we prefer the most specific hypothesis?
 What would happen if the examples are not consistent?
 What would happen if they have errors, noise?
 What if there is a hypothesis space H where one can find more that one
maximally specific hypothesis h?
 The search over the lattice must then be different to allow for this
possibility.

25. Summary FIND-S
 The input space is the space of all examples; the output space is the
space of all classes.
 A hypothesis maps examples into classes.
 We want a hypothesis close to target concept c.
 The input space establishes a partial ordering over the hypothesis
space.
 One can exploit this ordering to move along the corresponding
lattice.

26. Working Example: Mushrooms
Class of Tasks: Predicting poisonous mushrooms
Performance: Accuracy of Classification
Experience: Database describing mushrooms with their class
Knowledge to learn:
Function mapping mushrooms to {+,-}
where -:not-poisonous and +:poisonous
Representation of target knowledge:
conjunction of attribute values.
Learning mechanism:
candidate-elimination

27. Candidate Elimination
 The algorithm that finds the maximally specific hypothesis
is limited in that it only finds one of many hypotheses
consistent with the training data.
 The Candidate Elimination Algorithm (CEA) finds ALL
hypotheses consistent with the training data.
 CEA does that without explicitly enumerating all
consistent hypotheses.

28. Consistency vs Coverage
h1
h2
h1 covers a different set of examples than h2
h2 is consistent with training set D
h1 is not consistent with training set D
Positive examples
Negative examples
Training set D
-
-
-
-
+
+
++
+
+
+

29. Version Space VS
Hypothesis space H
Version space:
Subset of hypothesis from H consistent with training set D.

30. List-Then-Eliminate Algorithm
Algorithm:
1. Version Space VS: All hypotheses in H
2. For each training example X
Remove every hypothesis h in H inconsistent
with X: h(x) = c(x)
3. Output the version space VS
Comments: This is unfeasible. The size of H is unmanageable.

31. Previous Exercise: Mushrooms
Let’s remember our exercise in which we tried to classify
mushrooms as poisonous (+) or not-poisonous (-).
Training set D:
((red,small,round,humid,low,smooth), +)
((red,small,elongated,humid,low,smooth), +)
((gray,large,elongated,humid,low,rough), -)
((red,small,elongated,humid,high,rough), +)

32. Consistent Hypotheses
Our first algorithm found only one out of six
consistent hypotheses:
(red,small,*,humid,*,*)
(*,small,*,humid,*,*)(red,*,*,humid,*,*) (red,small,*,*,*,*)
(red,*,*,*,*,*) (*,small,*,*,*,*)G:
S:
S: Most specific
G: Most general

33. Candidate-Elimination Algorithm
(red,small,*,humid,*,*)
(red,*,*,*,*,*)(*,small,*,*,*,*)G:
S:
The candidate elimination algorithm keeps two lists
of hypotheses consistent with the training data:
The list of most specific hypotheses S and
The list of most general hypotheses G
This is enough to derive the whole version space VS.
VS

34. Candidate-Elimination Algorithm
• Initialize G to the set of maximally general hypotheses in H
• Initialize S to the set of maximally specific hypotheses in H
• For each training example X do
• If X is positive: generalize S if necessary
• If X is negative: specialize G if necessary
• Output {G,S}

35. Candidate-Elimination Algorithm
 Initialize G to the set of maximally general hypotheses in H
 Initialize S to the set of maximally specific hypotheses in H
 For each training example d, do
 If d+
 Remove from G any hypothesis inconsistent with d
 For each hypothesis s in S that is not consistent with d
 Remove s from S
 Add to S all minimal generalizations h of s such that h is consistent with
d and some member of G is more general than h
 Remove from S any hipothesis that is more general than another
hypothesis in S
 If d-
 Remove from S any hypothesis inconsistent with d
 For each hypothesis g in G that is not consistent with d
 Remove g from G
 Add to G all minimal specializations h of g such that h is consistent with
d and some member of S is more general than h
 Remove from G any hipothesis that is less general than another
hypothesis in G

36. Positive Examples
a) If X is positive:
 Remove from G any hypothesis inconsistent with X
 For each hypothesis h in S not consistent with X
 Remove h from S
 Add all minimal generalizations of h consistent with X
such that some member of G is more general than h
 Remove from S any hypothesis more general than
any other hypothesis in S
G:
S:
h
inconsistent
add minimal generalizations

37. Negative Examples
b) If X is negative:
Remove from S any hypothesis inconsistent with X
For each hypothesis h in G not consistent with X
Remove g from G
Add all minimal generalizations of h consistent with X
such that some member of S is more specific than h
Remove from G any hypothesis less general than any other
hypothesis in G
G:
S: h inconsistent
add minimal specializations

38. An Exercise
Initialize the S and G sets:
S: (0,0,0,0,0,0)
G: (*,*,*,*,*,*)
Let’s look at the first two examples:
((red,small,round,humid,low,smooth), +)
((red,small,elongated,humid,low,smooth), +)

39. An Exercise: two positives
The first two examples are positive:
((red,small,round,humid,low,smooth), +)
((red,small,elongated,humid,low,smooth), +)
S: (0,0,0,0,0,0)
(red,small,round,humid,low,smooth)
(red,small,*,humid,low,smooth)
G: (*,*,*,*,*,*)
generalize
specialize

40. An Exercise: first negative
The third example is a negative example:
((gray,large,elongated,humid,low,rough), -)
S:(red,small,*,humid,low,smooth)
G: (*,*,*,*,*,*)
generalize
specialize
(red,*,*,*,*,*,*) (*,small,*,*,*,*) (*,*,*,*,*,smooth)
Why is (*,*,round,*,*,*) not a valid specialization of G

41. An Exercise: another positive
The fourth example is a positive example:
((red,small,elongated,humid,high,rough), +)
S:(red,small,*,humid,low,smooth)
generalize
specialize
G: (red,*,*,*,*,*,*) (*,small,*,*,*,*) (*,*,*,*,*,smooth)
(red,small,*,humid,*,*)

42. The Learned Version Space VS
G: (red,*,*,*,*,*,*) (*,small,*,*,*,*)
S: (red,small,*,humid,*,*)
(red,*,*,humid,*,*) (red,small,*,*,*,*) (*,small,*,humid,*,*)

43. Points to Consider
 Will the algorithm converge to the right hypothesis?
 The algorithm is guaranteed to converge to the right hypothesis
provided the following:
 No errors exist in the examples
 The target concept is included in the hypothesis space H
 What happens if there exists errors in the examples?
 The right hypothesis would be inconsistent and thus eliminated.
 If the S and G sets converge to an empty space we have evidence that
the true concept lies outside space H.

44. Query Learning
Remember the version space VS after seeing our 4 examples
on the mushroom database:
G: (red,*,*,*,*,*,*) (*,small,*,*,*,*)
S: (red,small,*,humid,*,*)
(red,*,*,humid,*,*) (red,small,*,*,*,*) (*,small,*,humid,*,*)
What would be a good question to pose to the algorithm?
What example is best next?

45. Query Learning
 Remember there are three settings for learning:
 Tasks are generated by a random process outside the learner
 The learner can pose queries to a teacher
 The learner explores its surroundings autonomously
 Here we focus on the second setting; posing queries to an expert.
 Version space strategy: Ask about the class of an example that would
prune half of the space.
 Example: (red,small,round,dry,low,smooth)

46. Query Learning
 In general if we are able to prune the version space by
half on each new query then we can find an optimal
hypothesis in the following
 Number of steps: log2 |VS|
 Can you explain why?

47. Classifying Examples
 What if the version space VS has not collapsed into a
single hypothesis and we are asked to classify a new
instance?
 Suppose all hypotheses in set S agree that the instance is
positive.
 Then we are sure that all hypotheses in VS agree the instance is
positive. Why?
 The same can be said if the instance is negative by all members
of set G. Why?
 In general one can vote over all hypotheses in VS if there
is no unanimous agreement.

48. Inductive Bias
 Inductive bias is the preference for a hypothesis space H
and a search mechanism over H.
 What would happen if we choose an H that contains all
possible hypotheses?
 What would the size of H be?
 |H| = Size of the power set of the input space X.
 Example:
 You have n Boolean features. |X| = 2n
 And the size of H is 2^2^n

49. Inductive Bias
In this case, the candidate elimination algorithm would simply
classify as positive the training examples it has seen. This is
because H is so large, every possible hypothesis is contained
within it.
A Property of any Inductive Algorithm:
It must have some embedded assumptions about the
nature of H.
Without assumptions learning is impossible.

50. Summary
 The candidate elimination algorithm exploits the general-specific
ordering of hypotheses to find all hypotheses consistent with the
training data.
 The version space contains all consistent hypotheses and is simply
represented by two lists: S and G.
 Candidate elimination algorithm is not robust to noise and assumes
the target concept is included in the hypothesis space.
 Any inductive algorithm needs some assumptions about the
hypothesis space, otherwise it would be impossible to perform
predictions.

51. eduardopoggi@yahoo.com.ar
eduardo-poggi
http://ar.linkedin.com/in/eduardoapoggi
https://www.facebook.com/eduardo.poggi
@eduardoapoggi

52. Bibliografía
 Capítulo 2 de Mitchell