Presentation iaf 2014 v1

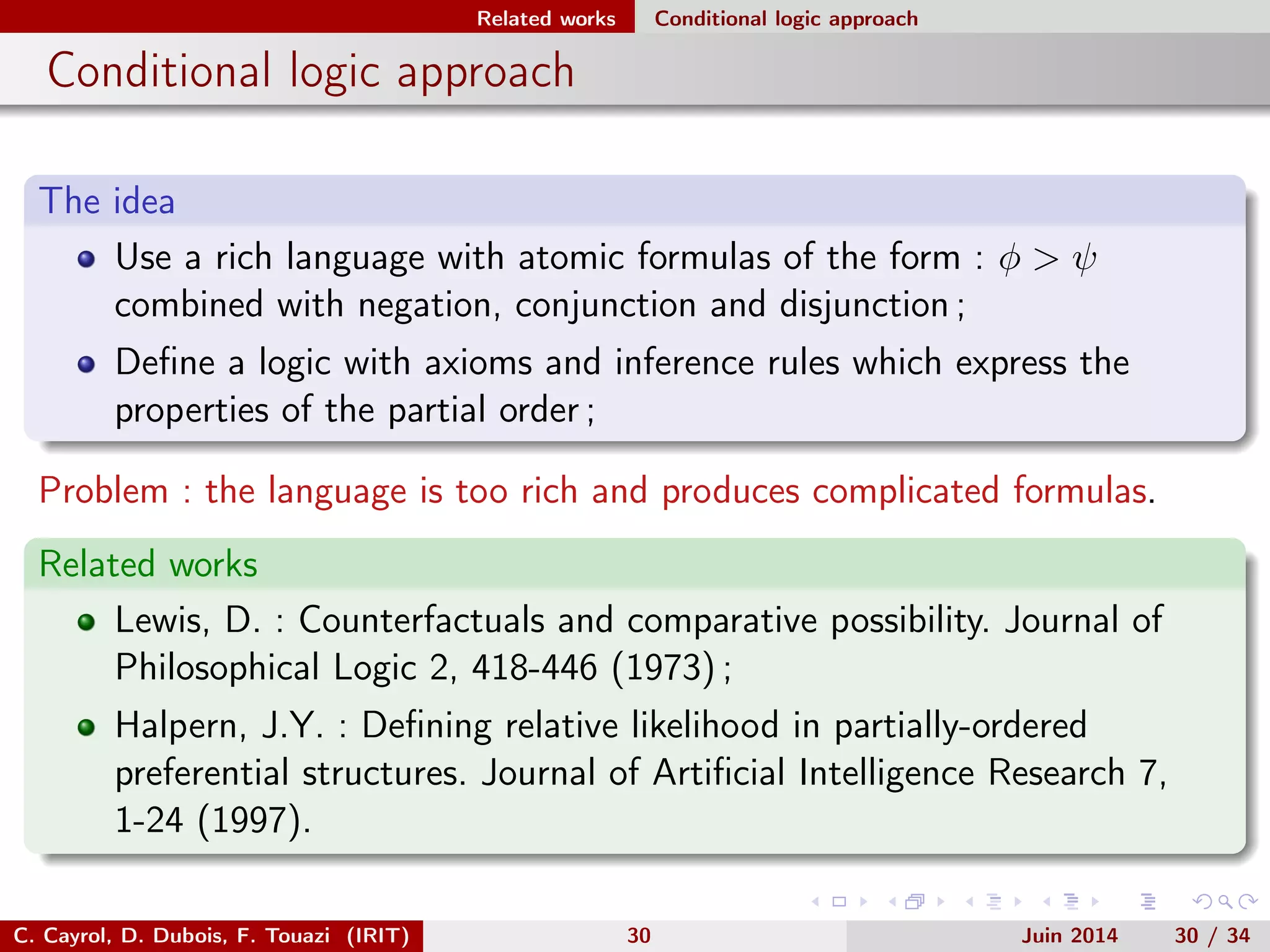
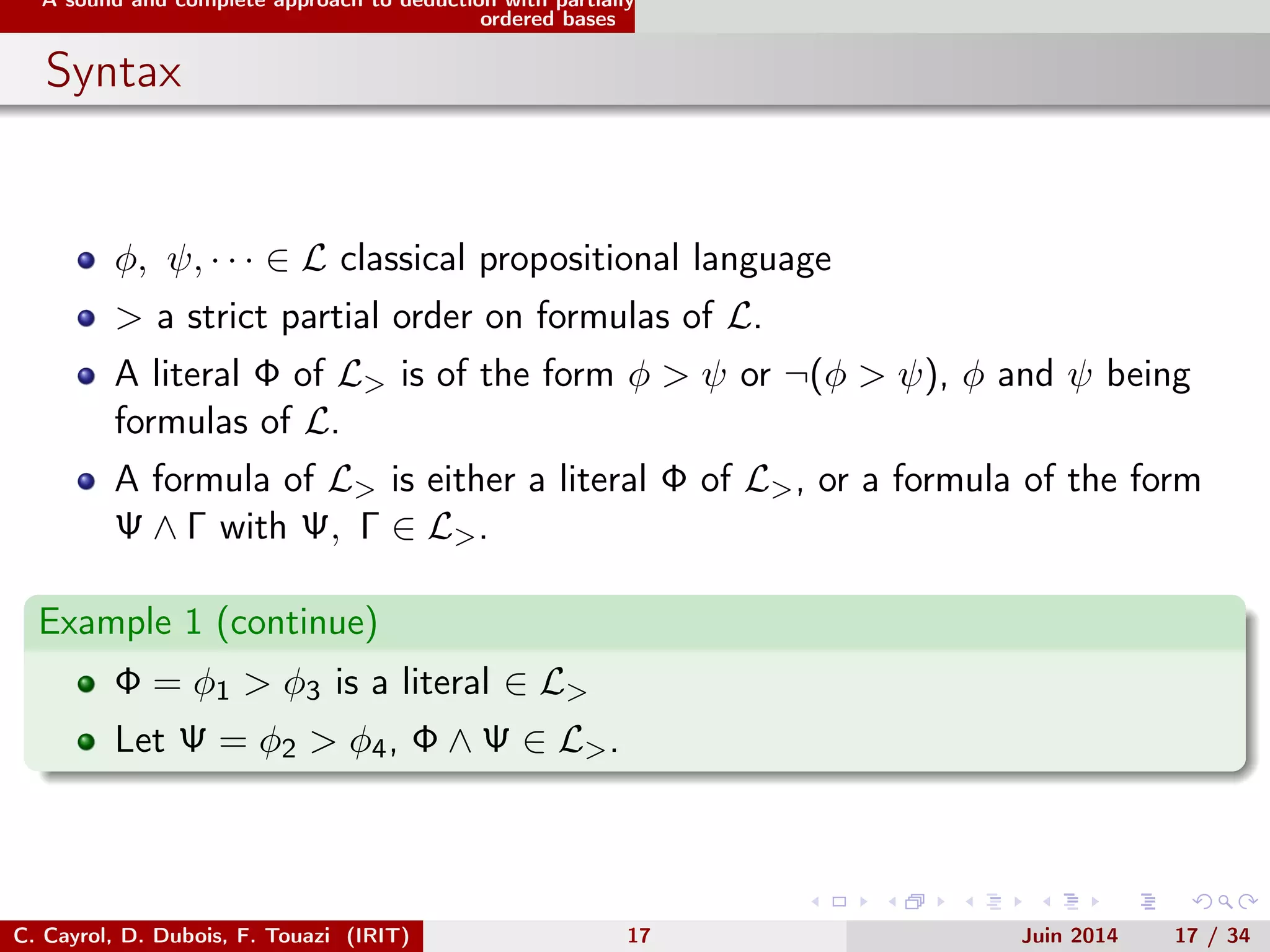
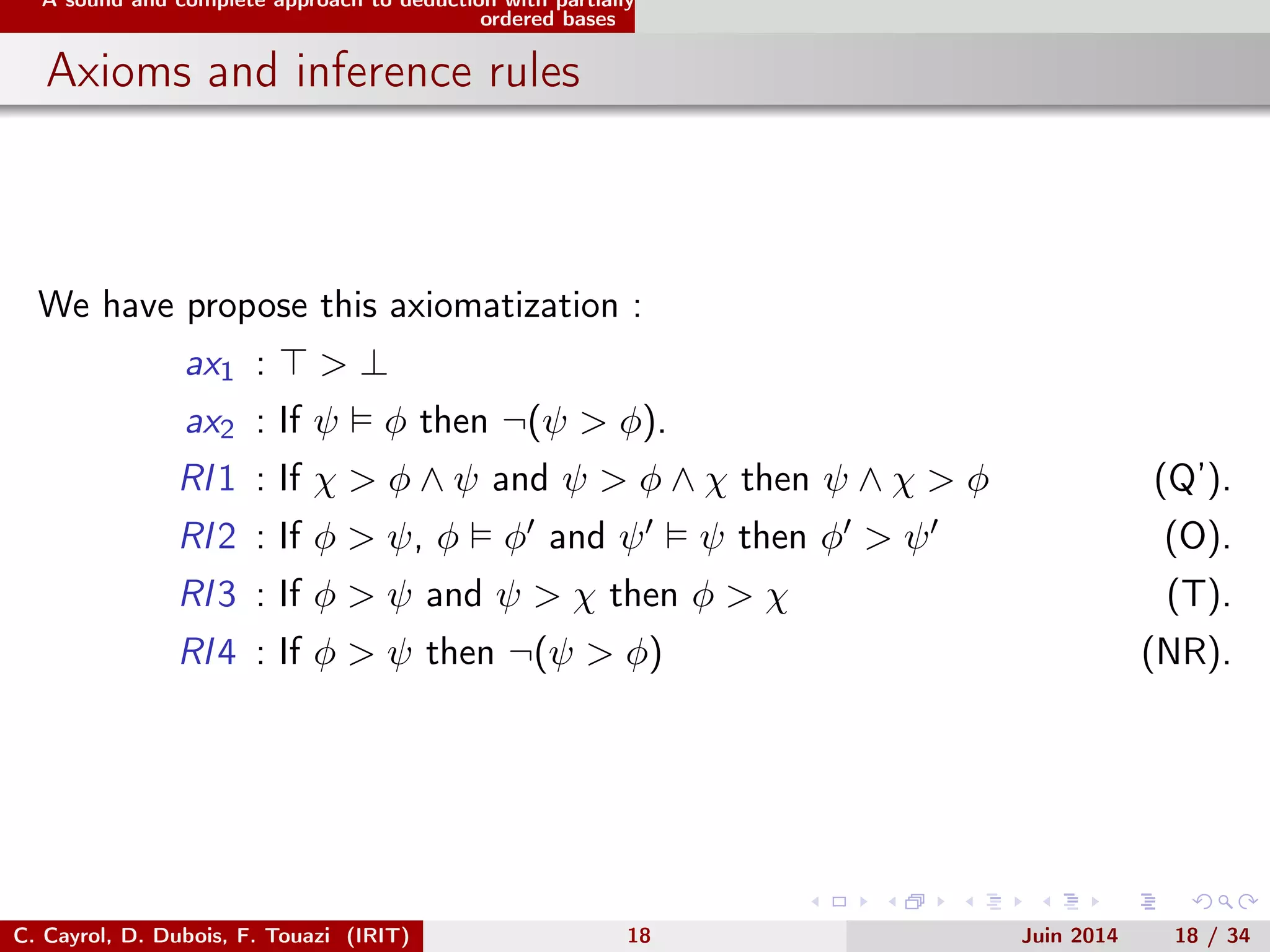
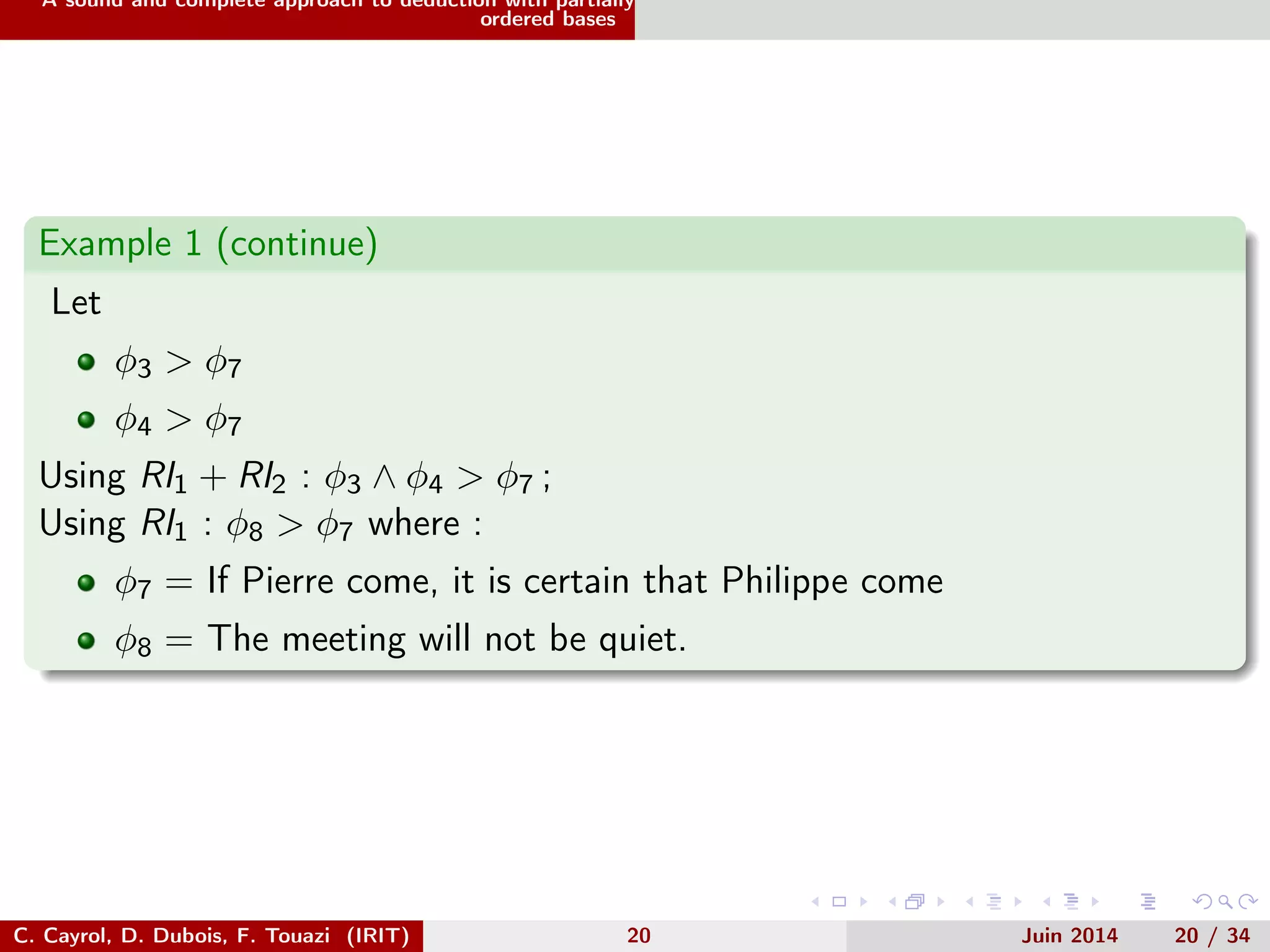
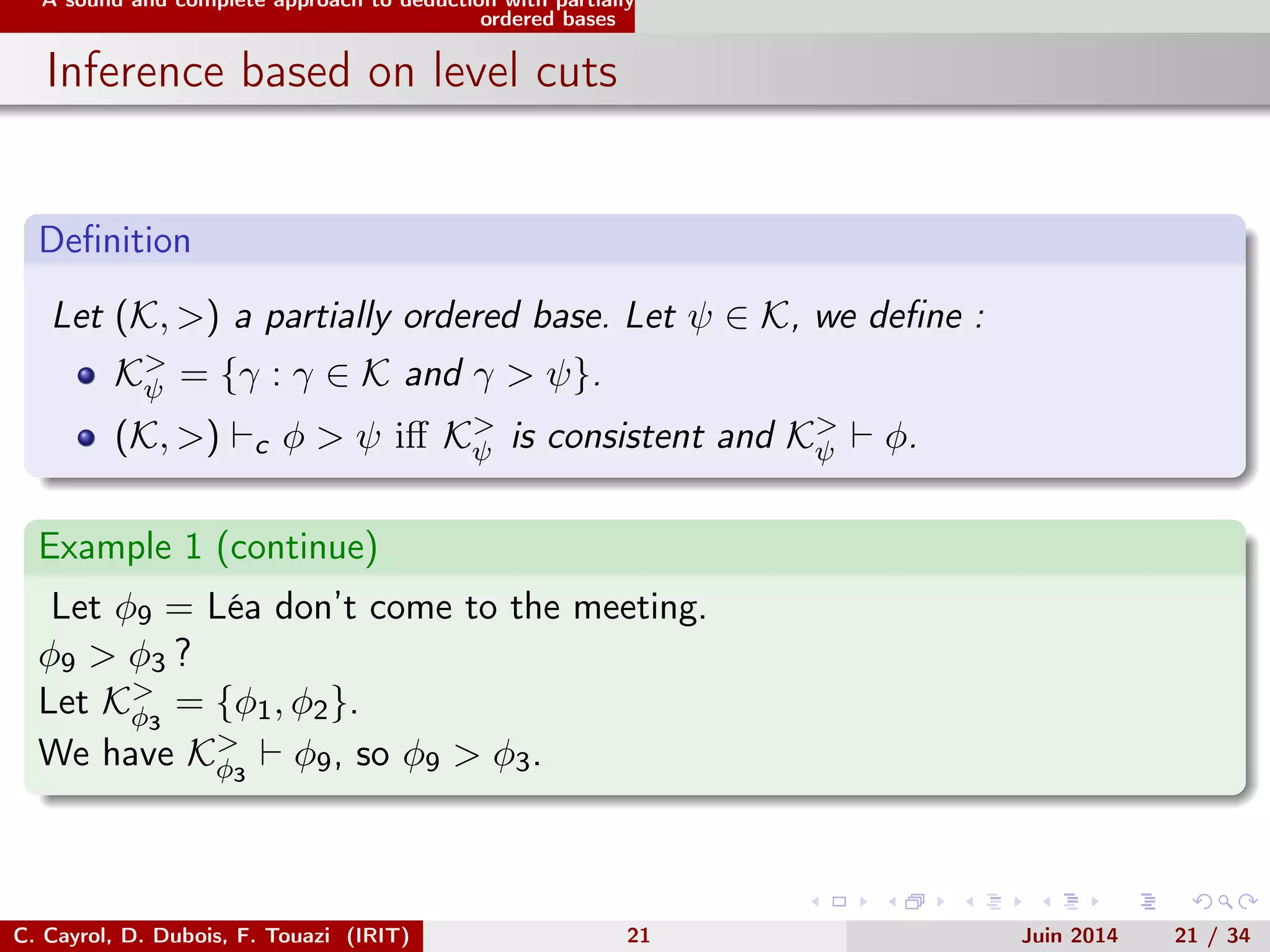
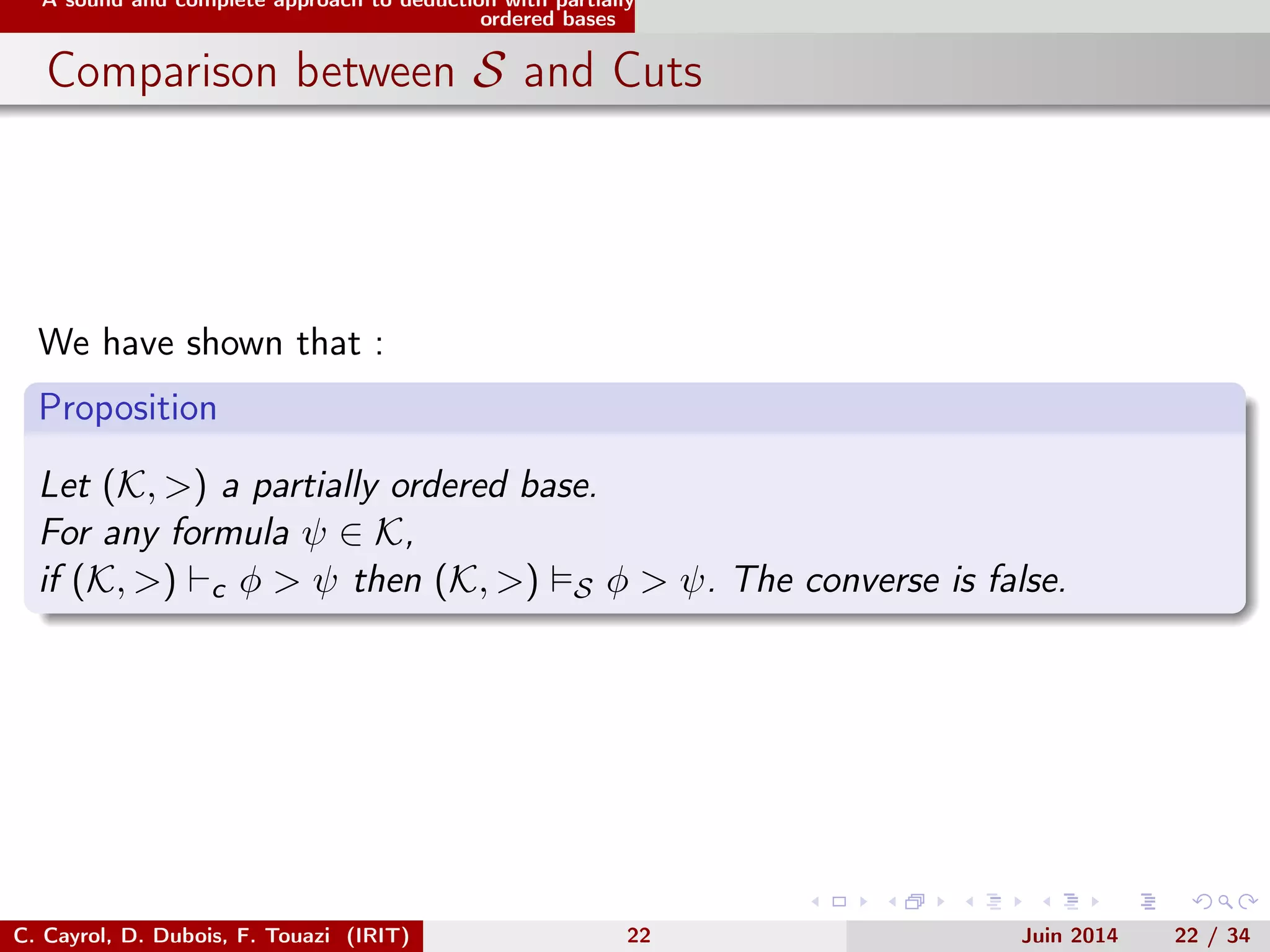
On the deductive closure of a partially ordered
propositional belief base
Claudette Cayrol Didier Dubois Fayçal Touazi
IRIT, University of Toulouse, France.
Juin 2014
JIAF
C. Cayrol, D. Dubois, F. Touazi (IRIT) 1 Juin 2014 1 / 34

Outline
1 Introduction
2 Background on Possibilistic logic
3 Semantics for partially ordered bases
4 A sound and complete approach to deduction with partially ordered
bases
5 Comparison with symbolic possibilistic approach
6 Related works
7 Conclusion

Introduction
Introduction
Reasoning from ordered bases
The basic concept of ordered knowledge base has been studied for two
decades in Artiﬁcial Intelligence
If totally ordered : Theophrastus, Rescher (1976), possibilistic logic
A total order on formulas induces a total order on the models
And conversely (a measure of possibility or necessity)
Goal
Find an adequate semantics on partially ordered bases.
Deﬁne a partially ordered deductive closure (partial order over the
language).

Introduction
Motivating example
Example 1
We suppose this knowledge base :
φ1 = If Bernard comes to the meeting, Léa don’t come
φ2 = Bernard come to the meeting
φ3 = If CLoé comes, it is certain that the meeting will not be quiet
φ4 = Cloé should come
φ5 = If Philippe comes to the meeting and Léa don’t come, it is
almost certain that the meeting will not be quiet
φ6 = It is almost certain that Léa or Pierre come
φ7 = If Pierre come, it is certain that Philippe come
We know that φ1 > {φ3, φ6} > φ7,φ2 > {φ3, φ6} > φ7 and φ5 > φ7.

Background on Possibilistic logic
Let Ω be the set of states of the world.
Boolean possibility distribution
Framework to represent incomplete information of the form v ∈ E.
Example of incomplete information
Let v = age (Peter). We know that v ∈ E = {20, 21, 22, 23, 24, 25} the set
of possible values (v = 20 or v = 21 or v = 22 or v = 23 or v = 24 or
v = 25).
This information is represented by a Boolean possibility distribution :
π(ω) =
1 if ω ∈ E
0 else
Possibilistic formula
Weighted extension of classical logic : (φ, αi ) with φ is a proposition in a
language L and 1≥ αi >0

Possibility and Necessity measures
Possibility measure
Let Π be the possibility measure that expresses how much an event is
possible :
Π(A) = max{π(ω)|ω ∈ A}
Necessity measure
Let N be the necessity measure that expresses how much an event is
certain :
N(A) = 1 − Π(¬A) = min{1 − π(ω)|ω /∈ A}
Characteristic properties
N(φ ∧ ψ) = min(N(φ), N(ψ))(axiom of N)
Π(φ ∨ ψ) = max(Π(φ), Π(ψ))(axiom of Π)

Totally ordered closure (equivalent syntactical construction)
Axioms and inference rules
Axioms of classical logic at degree 1.
(φ → (ψ → φ), 1) ;
((φ → (ψ → χ)) → ((φ → ψ) → (φ → χ)), 1) ;
((¬φ) → (¬ψ)) → (ψ → φ), 1) ;
Inference rules
Weakening rule : If α > β then (φ, α) (φ, β)
Modus Ponens : {(φ → ψ, α), (φ, α)} (ψ, α)
This system is correct and complete (Dubois, Lang, Prade, 1994).
Important remark
It may happen that if (φj , αj ) ∈ Σ then (φj , βj ) ∈ C(Σ) with βj > αj :
αj > αi ⇒ NΣ(φj ) > NΣ(φi )

Semantics for partially ordered bases
Strict weak optimistic dominance wos
Deﬁnition
A wos B iﬀ A = ∅ and ∀b ∈ B, ∃a ∈ A, a > b
Natural for relative likelihood (already, Halpern, 1977).
Proposition
Principal properties :
1 Qualitativeness (Q) ;
2 Orderliness (O) ;
Derived properties :
1 The reciprocal of (SU) ;
2 Negligibility (N) ;
3 Conditional Closure by Implication (CCI) ;
4 Conditional Closure by Conjunction (CCC) ;
5 Left Disjunction (OR), (CUT) and (CM) (Cumulativity).

Syntax and notations
Let L be a propositional language, K ⊂ L a finite set of formulas equiped
with a partial order >.
(K, >) is a set of constraints of the form φ > ψ ;
If φ, ψ ∈ K, φ > ψ is interpreted as " φ is preferred to ψ " (more
certain, higher priority) ;
K(ω) denotes the subset of formulas in K satisfied by the
interpretation ω ∈ Ω ; hence K(ω) is the subset of propositions
falsified by ω ∈ Ω ;
[φ] denotes the set of the models of φ, a subset of Ω.

Deductive closure based on the optimistic relation
Definition
From (K, >) to (Ω, ) ∀ω, ω ∈ Ω, ω ω iff K(ω ) >wos K(ω) iff
∀ψ ∈ K(ω), ∃φ ∈ K(ω ), φ > ψ
From (Ω, ) to (L, N) ∀φ, ψ ∈ L, φ N ψ iff [ψ] wos [φ] iff
∀ω ∈ [φ], ∃ω ∈ [ψ], ω ω .
These definitions interpret (K, >) as a certainty ordering, in agreement
with possibilistic logic.
Deductive closure of a partially ordered base
The partially ordered deductive closure of (K, >) can be defined by
C(K, >) N
= {(φ, ψ) ∈ L2
: φ N ψ}.
And we denote (φ, ψ) ∈ C(K, >) N
by K |=wos φ N ψ.

Counter-Example
This example shows the semantic deﬁnition of deductive closure is
problematic.
Example 1
Let (K, >) = {¬x ∨ y > x ∧ y > ¬x, x > ¬x} be a partially ordered base,
where > is the strict partial order.
Let us apply the previous deﬁnitions :
From (K, >) to (Ω, ) : we obtain xy {¯xy, x¯y, ¯x¯y} ;
From (Ω, ) to (L, N), we obtain :
x N ¬x,
x ∧ y N ¬x ;
¬x ∨ y N ¬x ;
but not ¬x ∨ y N x ∧ y.
We have lost the piece of information ¬x ∨ y > x ∧ y

What is wrong
Let us interpret the partial order of K as stemming from a partial order
on interpretations, via wos :
[x ∧ y] wos [¬x ∨ ¬y] ;
[¬x] wos [x ∧ y] ;
[¬x] wos [x].
It is easy to see that these constraints imply that :
xy {¯xy, x¯y, ¯x¯y}
(¯xy x¯y) ∨ (¯x¯y x¯y) (a disjunctive constraint)
Problem
More informative than the constraint on the partial order , but the
disjunction is not representable via a single partial order.

A sound and complete approach to deduction with partially
ordered bases
Syntax
φ, ψ, · · · ∈ L classical propositional language
> a strict partial order on formulas of L.
A literal Φ of L> is of the form φ > ψ or ¬(φ > ψ), φ and ψ being
formulas of L.
A formula of L> is either a literal Φ of L>, or a formula of the form
Ψ ∧ Γ with Ψ, Γ ∈ L>.
Example 1 (continue)
Φ = φ1 > φ3 is a literal ∈ L>
Let Ψ = φ2 > φ4, Φ ∧ Ψ ∈ L>.

ordered bases
Axioms and inference rules
We have propose this axiomatization :
ax1 : > ⊥
ax2 : If ψ φ then ¬(ψ > φ).
RI1 : If χ > φ ∧ ψ and ψ > φ ∧ χ then ψ ∧ χ > φ (Q’).
RI2 : If φ > ψ, φ φ and ψ ψ then φ > ψ (O).
RI3 : If φ > ψ and ψ > χ then φ > χ (T).
RI4 : If φ > ψ then ¬(ψ > φ) (NR).

ordered bases
Semantic
Deﬁnition (Semantic)
A model M is a structure (2Ω, ) where is a strict partial order on
2Ω satisfying the properties O and Q.
M S (φ > ψ) iﬀ [ψ] [φ].
We have show that :
Proposition
Let (K, >) a partially ordered base
Soundness :
(K, >) S φ > ψ ⇒ (K, >) S φ > ψ
Completeness :
(K, >) S φ > ψ ⇒ (K, >) S φ > ψ

ordered bases
Let
φ3 > φ7
φ4 > φ7
Using RI1 + RI2 : φ3 ∧ φ4 > φ7 ;
Using RI1 : φ8 > φ7 where :
φ7 = If Pierre come, it is certain that Philippe come
φ8 = The meeting will not be quiet.

ordered bases
Inference based on level cuts
Definition
Let (K, >) a partially ordered base. Let ψ ∈ K, we define :
K>
ψ = {γ : γ ∈ K and γ > ψ}.
(K, >) c φ > ψ iff K>
ψ is consistent and K>
ψ φ.
Let φ9 = Léa don’t come to the meeting.
φ9 > φ3 ?
Let K>
φ3
= {φ1, φ2}.
We have K>
φ3
φ9, so φ9 > φ3.

ordered bases
Comparison between S and Cuts
We have shown that :
Proposition
Let (K, >) a partially ordered base.
For any formula ψ ∈ K,
if (K, >) c φ > ψ then (K, >) S φ > ψ. The converse is false.

Comparison with symbolic possibilistic approach
Encoding a partially ordered base as a symbolic
possibilistic base
We start from a partially ordered base (K, >) :
Replace φ > ψ by (φ, ι(φ)) and (ψ, ι(ψ)) where ι(φ) is an ill-known
weight ∈ [0, 1], and ι(φ) > ι(ψ)
Deﬁnition
Let (K, >) a partially ordered base. (K, >) is encoded by
ΣK = {(φ, η(φ)), φ ∈ K}
C = {a > b/(φ, a), (ψ, b) ∈ ΣK and φ > ψ ∈ K}.
We can apply proof methods of possibilistic logic
Σ χ > ξ iﬀ NΣ(χ) > NΣ(ξ)
We do get a partial order on the language

However, this kind of encoding may add some unwanted information, as
shown by the following example.
Example
Let (K, >) = {¬x ∨ y > x ∧ y}.
ΣK = {(¬x ∨ y, a), (x ∧ y, b)} and C = {a > b}.
We can replace (x ∧ y, b) by (x, b), (y, b), Σ = {(¬x ∨ y, a), (x, b), (y, b)}
However, from ¬x ∨ y > x ∧ y, we can deduce neither ¬x ∨ y > x nor
¬x ∨ y > y using inference system S.
Remark
We consider only clausal bases

Encoding a symbolic possibilistic base as a partially ordered
base
We start from a partially ordered base (Σ, C) :
Deﬁnition
Let (Σ, C) be a symbolic possibilistic base and
Σ∗ = {φ : ∃a > 0, (φ, a) ∈ Σ} the corresponding set of formulas. The
coherent base associated to (Σ, C) is
Σ+
= {(φ, NΣ(φ)) : φ ∈ Σ∗
}.
Deﬁnition
A symbolic possibilistic base (Σ, C) is encoded by :
(K, >)Σ = {φ > ψ : (φ, w) ∈ Σ+, (ψ, w ) ∈ Σ+ and
C w > w } ∪ {φ > ⊥ : (φ, w) ∈ Σ+ and C w > Inc(Σ)}.

Comparison results
We have shown that :
Proposition
Let (Σ, C) be a symbolic possibilistic base and (K, >)Σ its encoding. Let
ψ ∈ K be such that ψ = ⊥, we have :
(Σ, C) φ > ψ iﬀ K>
ψ φ.
and also :
Proposition
Let (Σ, C) be a symbolic possibilistic base and (K, >)Σ its encoding.
(K, >)Σ S φ > ψ ⇒ (Σ, C) φ > ψ

Related works Partial order as a family of total orders
Partial order as a family of total orders
The idea
Consider the partial order > as a family of total orders >i , i = 1, . . . , n
extending it.
A partially ordered knowledge base (K, >) is then viewed as a
collection (K, >i ) of totally ordered ones.
Consider their possibilistic closures Ci (K) where formulas have weights
Ni (φ).
Cautious closure φ ψ iﬀ ∀i = 1, . . . , n, Ni (φ) > Ni (ψ)
Bold closure φ ψ iﬀ ∃i = 1, . . . , n, Ni (φ) > Ni (ψ)
Related work
Yahi, S. et al. : A lexicographic inference for partially preordered belief
bases. KR 2008, pp. 507-517.

Related works Conditional logic approach
Conditional logic approach
The idea
Use a rich language with atomic formulas of the form : φ > ψ
combined with negation, conjunction and disjunction ;
Define a logic with axioms and inference rules which express the
properties of the partial order ;
Problem : the language is too rich and produces complicated formulas.
Related works
Lewis, D. : Counterfactuals and comparative possibility. Journal of
Philosophical Logic 2, 418-446 (1973) ;
Halpern, J.Y. : Defining relative likelihood in partially-ordered
preferential structures. Journal of Artificial Intelligence Research 7,
1-24 (1997).

Related works Conditional logic approach
Reasoning with consistent subsets
The idea
A partial order > on K is just used to select preferred consistent
subsets of formulas ;
The inference (K, >) φ is deﬁned by : φ is consequence of all the
preferred subsets of formulas.
The deductive closure is then a classical set of accepted beliefs ;
This approach does not enable to deduce preferences between formulas,
but essentially extracts accepted beliefs.
Related works
Benferhat, S., Lagrue, S., Papini, O. : Reasoning with partially ordered
information in a possibilistic logic framework. Fuzzy Sets and Systems 144,
25-41 (2004).

Conclusion
Conclusion and Future works
Extending possibilistic logic to the partially ordered case is not
straightforward : we have used the idea of lifting a partial order from
elements to subsets, typical of possibilistic logic, but flaws, specific to
the partially ordered case, have been laid bare.
Define more faithful semantics for such partially ordered bases : a
partial order over the power set of the set of interpretations, not on
interpretations.
Define an appropriate syntactic inference, in a less expressive language
Compare the syntactical approach with the existing ones
Apply these results to the revision and the fusion of beliefs, as well as
preference modeling.

Conclusion

Presentation iaf 2014 v1

More Related Content

What's hot

Similar to Presentation iaf 2014 v1

Presentation iaf 2014 v1