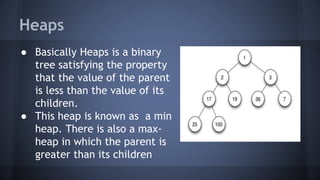
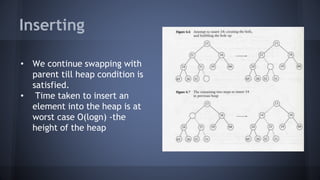
This document discusses heaps and their implementation and applications. It begins by defining heaps as binary trees where the value of each parent node is less than its children, forming a min heap. It then discusses the key properties of heaps, including finding the minimum element in O(1) time. The document goes on to describe implementing a heap using an array and the basic operations of insertion, deletion, and heapsort in O(logn) time. It concludes by discussing the advantages of heaps for fast insertion and removal and their applications in priority queues and sorting.

1. Placement Preparation
Heaps
Varun Raj
B.Tech, CSE

2. Heaps
● Basically Heaps is a binary
tree satisfying the property
that the value of the parent
is less than the value of its
children.
● This heap is known as a min
heap. There is also a max-heap
in which the parent is
greater than its children

3. Property of Heap
● The minimum element is found at the
root.Proof is trivial
● The maximum element is found at the
leaf.
● Hence time to find the minimum element
in the array is O(1)

4. Implementing a Heap
There are two most common ways to implement
a heap-
• Using an Array .We will use this since it is
more intuitive and simpler
• Using Linked List by struct. This is also
another method but I personally feel this is
an unnecessary complication

5. Implementation
Some Basic Implementation Concepts
• Generally in an array we start indexing from 0
in C++ but for heaps it is more convenient to
start numbering of the root from 1.
• For a particular node i its left child will be 2*i
and its right child will be 2*i+1 and its parent
will be i/2 irrespective of i being odd or even

6. Inserting
• We continue swapping with
parent till heap condition is
satisfied.
• Time taken to insert an
element into the heap is at
worst case O(logn) -the
height of the heap

7. Creating a heap
Method 1 using insert
• Starting from the insert method described
earlier to insert elements
• Time complexity from this method however
comes out to be log1+log2+…logn
=log(n!)=Theta (nlogn). Therefore we need
something faster

8. Heapify Procedure
• Opposite of insert procedure.
• You come down the heap instead
of moving up
• Time complexity is again O(logn).
• Therefore first create a normal
array and apply heapify to all the
elements of the array. Time
complexity is O(n).

9. Deleting an element from the heap
● In a heap ,normally you can
only delete from the root.
● So you delete from the root and
swap the last element of the
heap with it and then you do a
heapify on the root.
● Time complexity is again
O(logn)

10. Heapsort
• Since the element at the root is always the smallest we
print the element at the top and delete the root.
• The next element at the root will be the second
smallest element continuing like this we can sort the
entire array
• Since the time taken for deletion is O(logn). Therefore
time taken for n deletions is O(nlogn)
• Therefore time taken for heapsort is
O(n)+O(nlogn)=O(nlogn)

11. Advantages of Heaps
• Can sort in O(nlogn) time that is as fast as merge sort
but without using extra space
• Can insert elements in O(logn) time compare that with
sorted array.
• Can remove the smallest element in O(logn) time faster
than sorted array.

12. Applications of Heaps
• Very useful if you want a data structure that is used for
lots of insertions by value
• Is used in the implementation of priority queue
• Is also used for sorting