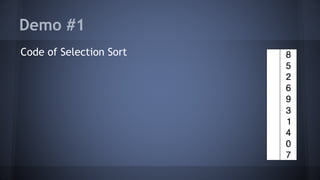
This document provides an overview of sorting algorithms including selection sort, bubble sort, insertion sort, merge sort, and heapsort. It discusses the time and space complexity of each algorithm, with merge sort having the best time complexity of O(n log n). Code examples and exercises are provided to help understand how each algorithm works. The goal is to help students learn common sorting techniques needed for coding interviews and problems.

1. Placement Preparation
Sorting and Heaps
Varun Raj
B.Tech, CSE

2. Prerequisites
• You must know array properly.
• You must be familiar with pointers and writing basic
loops
• You must have some basic idea of time complexity

3. Aim of Lecture
● Selection Sort/Bubble Sort
● Insertion Sort
● Merge Sort
● Heaps and Heapsort
● Quick Sort (If possible)

4. Motivation
Sorting is any process of arranging items according to value.
In computer science, sorting is one of the most extensively
researched subjects because of the need to speed up the operation
on thousands or millions of records during a search operation

5. The real reason.
● The real reason we are studying sorting is because be
it any coding question in any interview the candidate
is expected to know the basic of the sorting and
sorting questions are the most expected questions to
be asked

6. Selection Sort
The most intuitive sorting algorithm.
Works by selecting the smallest element of the
array and placing it at the head of the array.
Then the process is repeated for the remainder
of the array the next smallest element is
selected and put into the next slot, and so on
down the line

7. Demo #1
Code of Selection Sort

8. Exercise #1
● Write a program that does selection sort on a set of
integers
● Some pointers-
● You will need two loops
● You will need a variable that stores the current
minimum and then you will have to swap it with the
head.

9. Analysing Complexity
• In the 1st step the algorithm the for loop runs n-1
times.
• In the second step the for loop runs n-2 times since the
1st element is set
• Hence the time taken is n-1+n-2+n-3……..+1=n*(n-1)/2
That is O(n^2)
• The thing to note is that the complexity is O(n^2) for
best, average and worst case.
• The space complexity is O(1) that is no extra space is
used since the algorithm works only on the input array

10. Bubble Sort
The bubble sort works by iterating
down an array to be sorted from the
first element to the last, comparing
each pair of elements and switching
their positions if necessary. This
process is repeated as many times as
necessary, until the array is sorted

11. Demo #2
Code For Bubble Sort

12. Exercise #2
● Write a program that does bubble sort on a set of
integers
● Some pointers-
● You will need two loops
• At the end of 1st step the maximum reaches the last
position .At the end of second step the 2nd maximum
reaches the 2nd last position

13. Analysing Complexity for Bubble Sort
• In the 1st step the algorithm the for loop runs n times.
• In the second step the for loop runs n-1 times since the
1st element is set
• Hence the time taken is n+n-1+n-2……..+1=n*(n+1)/2
That is O(n^2)
• The thing to note is that the complexity is O(n^2) for
best, average and worst case.
• The space complexity is O(1) that is no extra space is
used since the algorithm works only on the input array

14. Some Improvements To Bubble Sort
On Close Observation we observe that even in the best
case Bubble Sort takes O(n^2) time this can be reduced to
O(n) that is in a perfectly sorted array bubble sort will
only take O(n) time to terminate(which is already sorted)
The idea behind this is that at each outer loop iteration
keep a counter so that if in it’s inner loop iteration no
swapping was done this means that the array is already
sorted and no further outer loop iterations need to be
done and the array is sorted.So terminate the code

15. Demo #3
● This improves only the best case running time of bubble sort the
worst case still remains O(n^2)
● The complexity is O(n^2) for average and worst case.
● For best case complexity is O(n) that is already sorted array

16. Insertion Sort
It inserts each element of the array
into its proper position, leaving
progressively larger stretches of the
array sorted

17. Demo
Code for insertion sort

18. Analysing Complexity for Insertion
Sort
• In the 1st step the algorithm the for loop runs 0 times.
• In the second step the for loop runs 1 times (worst
case) Hence the time taken is 1+2+3….n-1=n*(n-1)/2
That is O(n^2) (worst case)
• The thing to note is that the complexity is O(n^2) for
average and worst case.
• The best case time complexity is O(n).
• The space complexity is O(1) that is no extra space is
used since the algorithm works only on the input array

19. Merge Sort
MergeSort is a Divide and
Conquer algorithm. It divides input array in
two halves, calls itself recursively for the
two halves and then merges the two sorted
halves.

20. Merge Sort-Intiution
The main concept here is
recursion
The Merge Sort takes an
array from 1 to n and calls
itself on the array [1,n/2]
and [n/2+1,n] recursively
both these subparts are
sorted so too sort two
completely sorted list we
only merge them

21. Demo
Code for merge sort
Its little complicated so I would like you to practise
properly
Some common errors
• Base case of recursion
• Problems with merging especially when one half
crosses the midpoint (Explained)

22. Analysing Complexity for Merging
Sort
• There is some trick involved in finding the time complexity of
Merge Sort . The time complexity is O(nlogn) Here log refers to
base 2.
• Proof-
• T(n)=2*T(n/2) +cn where c is any constant
• The solution to this equation is k*nlogn the proof follows from
substitution and something you can look up online or I can do on
the board.
• The space complexity of this algorithm is O(n) since we are using
an extra array

23. Some remarks about Merge Sort
• Merge Sort is the fastest algorithm you have seen till now.Its
complexity is O(n*logn) and for large n it is faster than any
quadratic algorithm for large input
• Sometimes for small input merge sort may become slower than
insertion sort due to constant factors.Hence for small input prefer
insertion sort
• The space complexity is O(n) that is an extra array is required this
is the price we had to pay for a faster algorithm.
• We will see now that Heaps offer us time complexity of O(nlogn)
with no extra space required but it has a little sophisticated code.

24. Some Concluding Remarks -
● We learnt 3 quadratic time sorting algorithms –Selection Sort,
Insertion Sort, Bubble Sort
● We learnt to optimise bubble sort for best case
● The general advice is that whenever using a quadratic time
algorithm use insertion sort. (The reason for this is given as an
exercise at the last slide)
● Merge Sort trumps all the algorithm given large enough input,
however for input as small as 10 insertion sort will be faster

25. Extra Questions
I am not going to discuss the answer to these questions in the class,
however you could ask this question on facebook group or personally
message me.
These questions are for personal enhancement , maybe you could
encounter this question in the placement interview/test maybe not
• Insertion Sort-Prove that the time complexity of insertion sort is
O(n+x) where x is the number of inversions in the input array.Here
inversion refers to the pair (ai, aj) with i<j but ai >aj.
• Merge Sort- The time complexity of Merge Sort is O(nlogn) .Prove
that no sorting algorithm in the world that uses comparision
sorting can be asymptotically faster than this