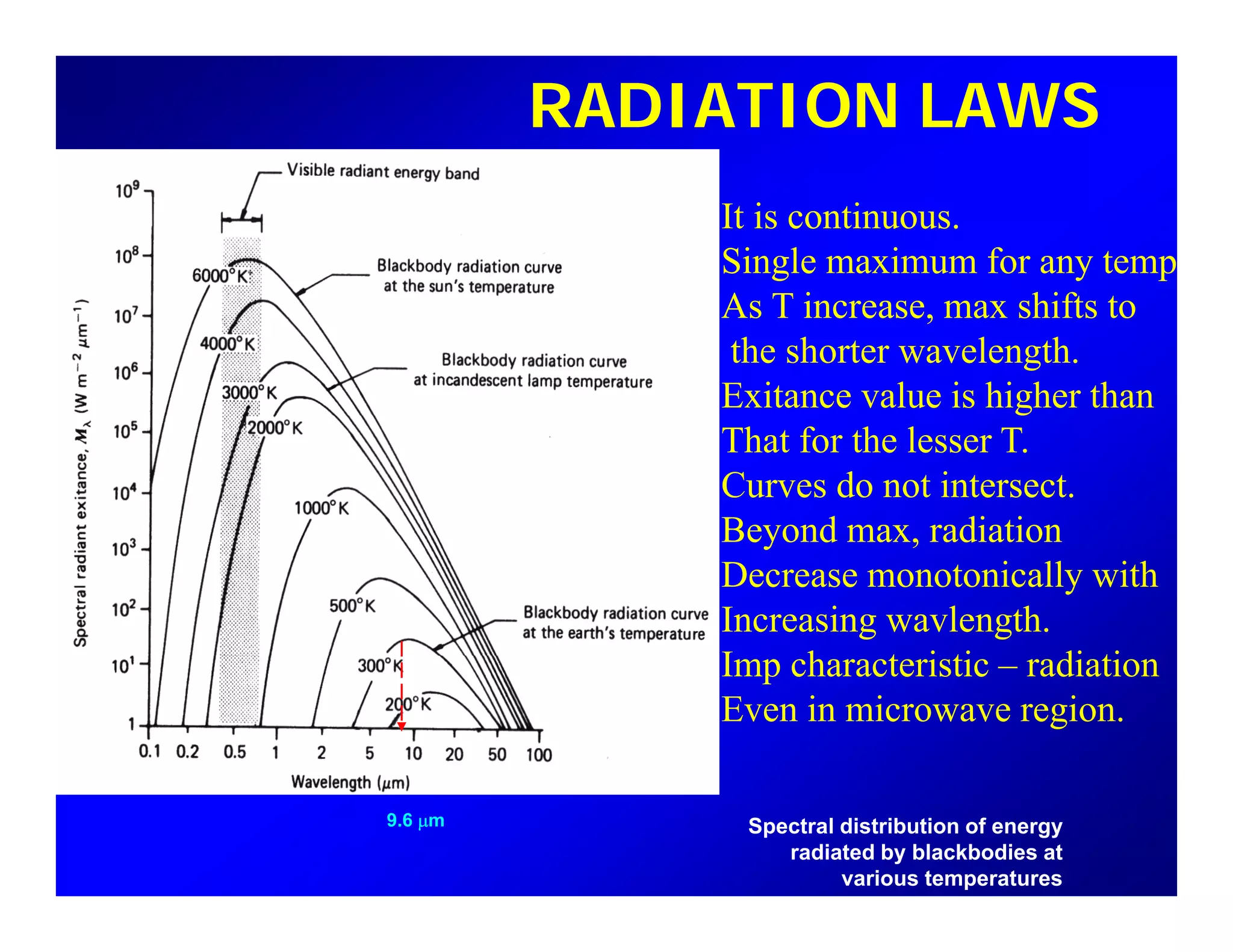
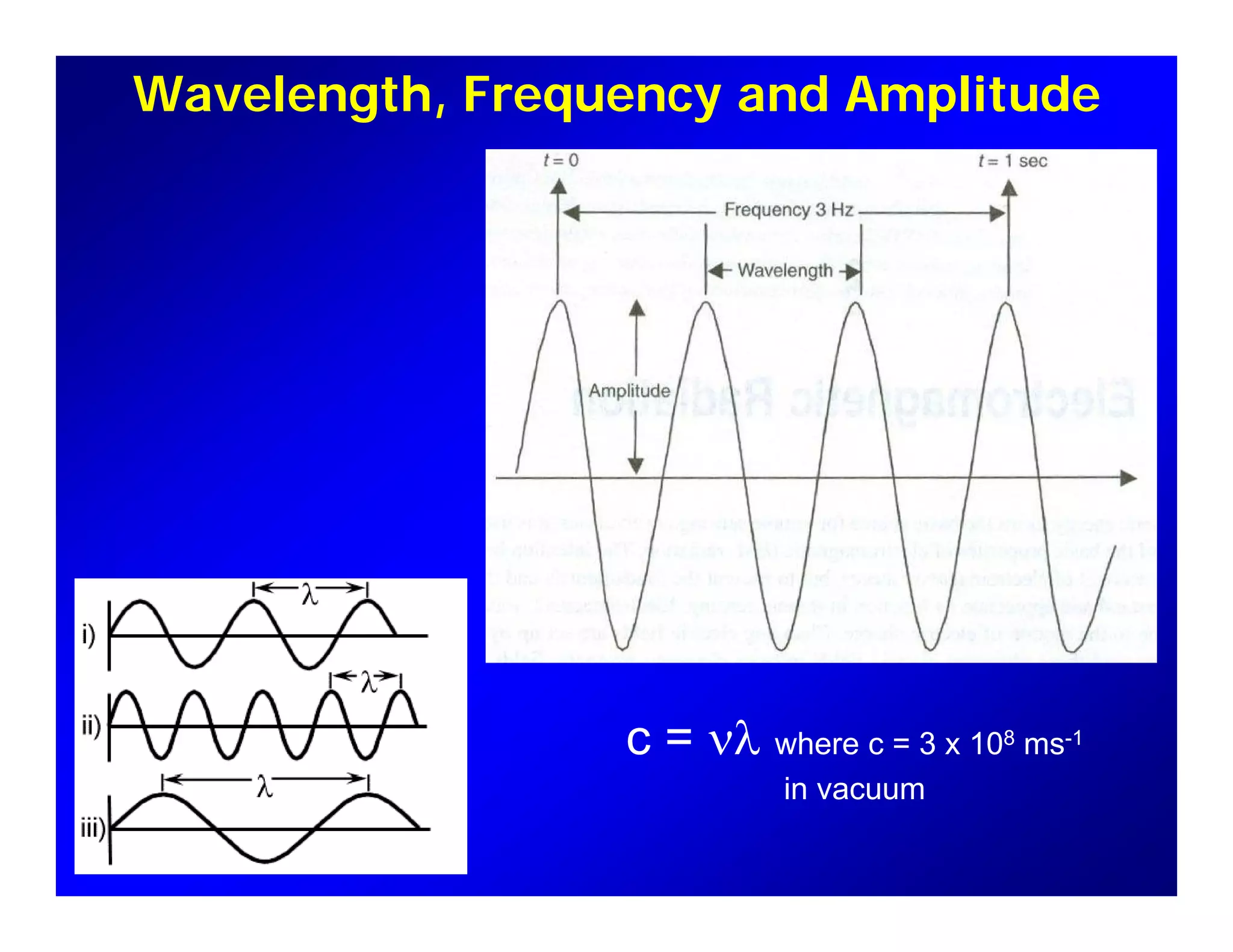
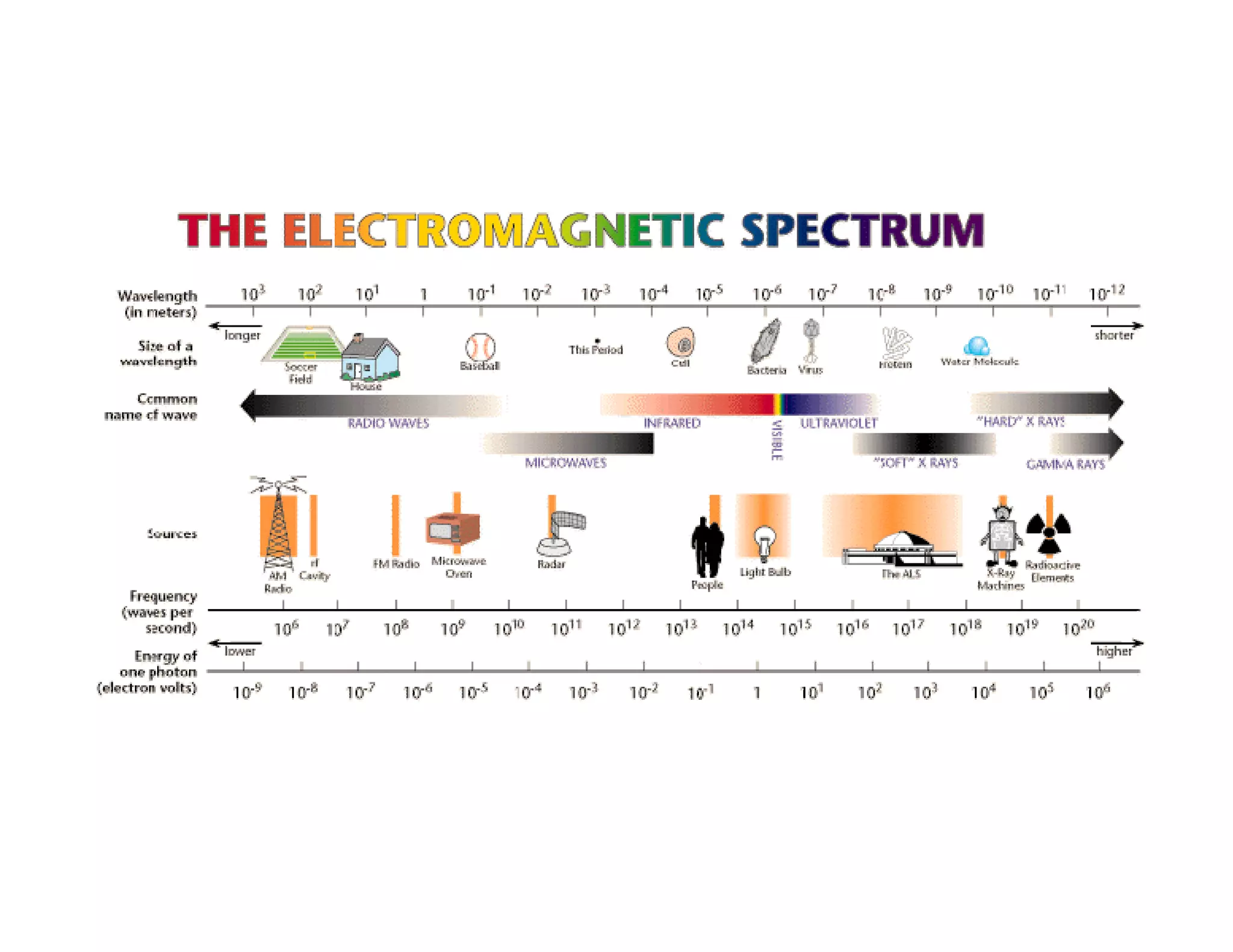
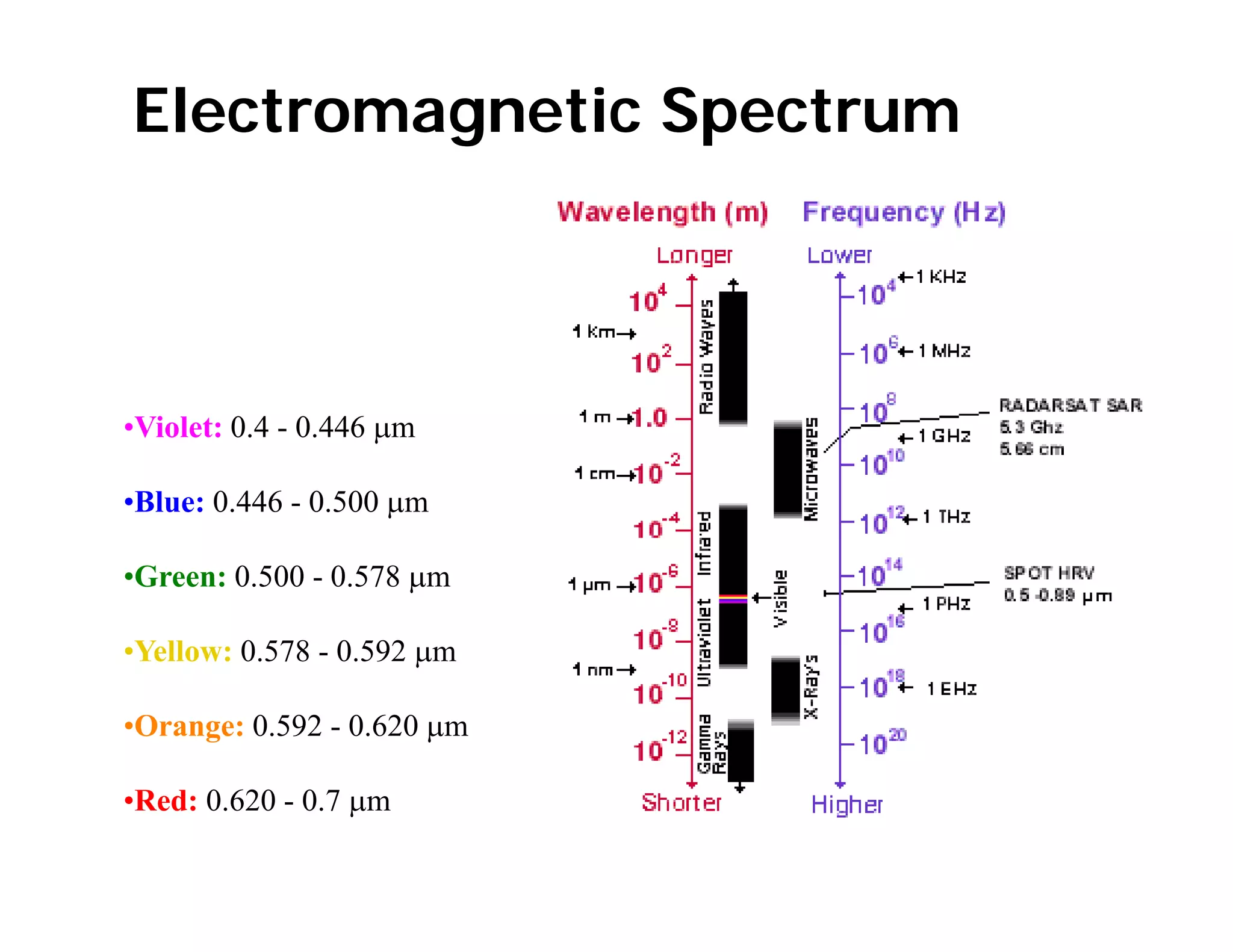
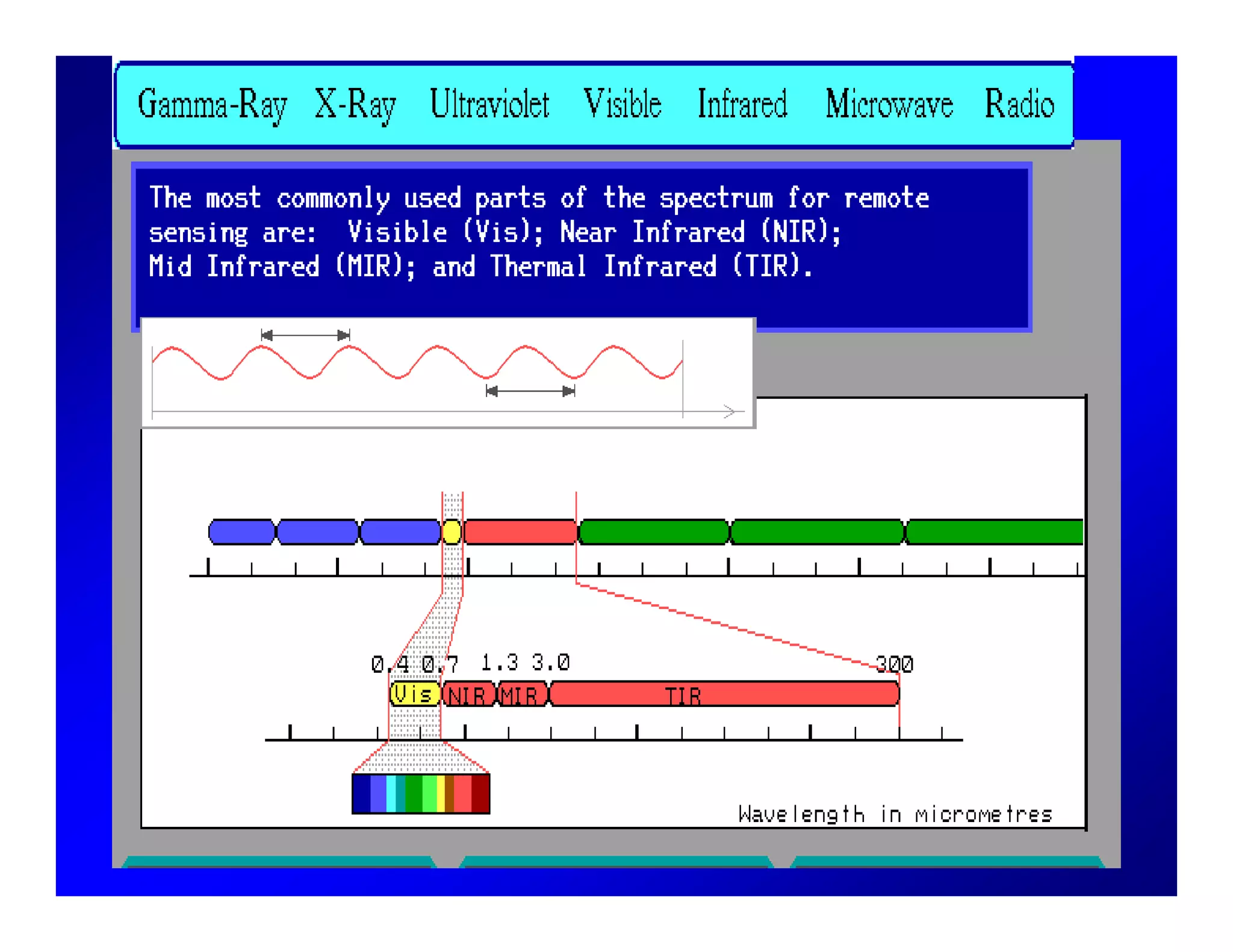
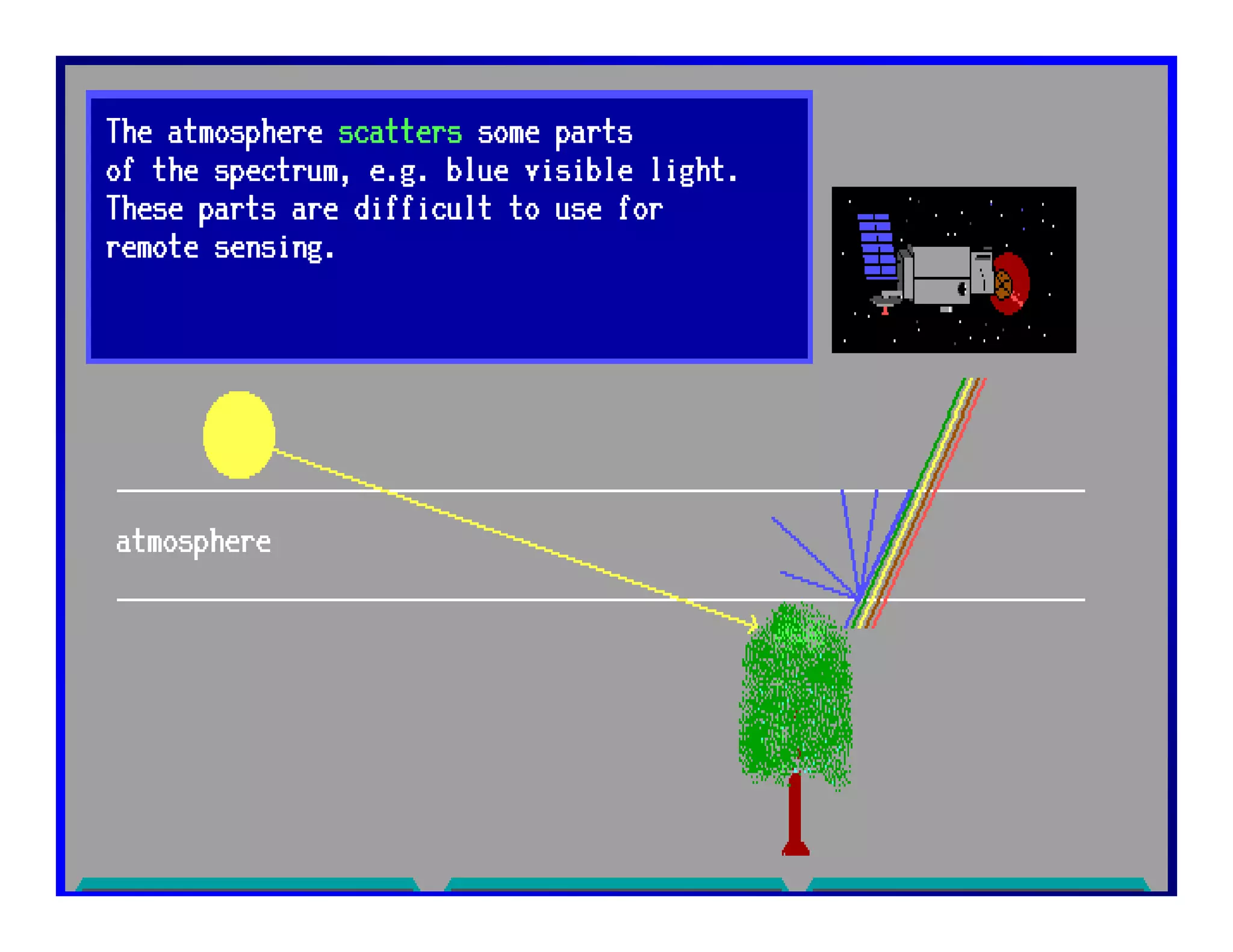
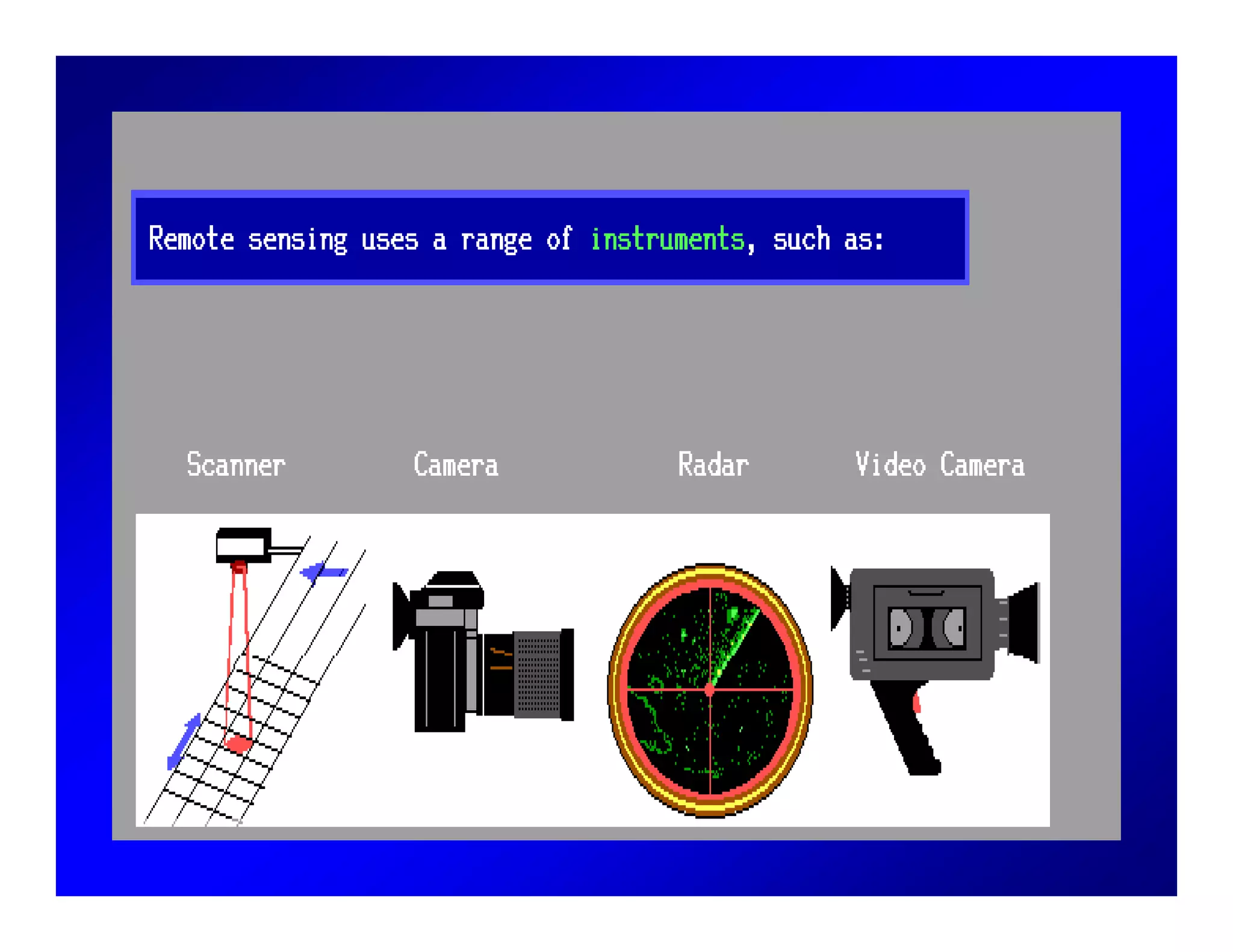
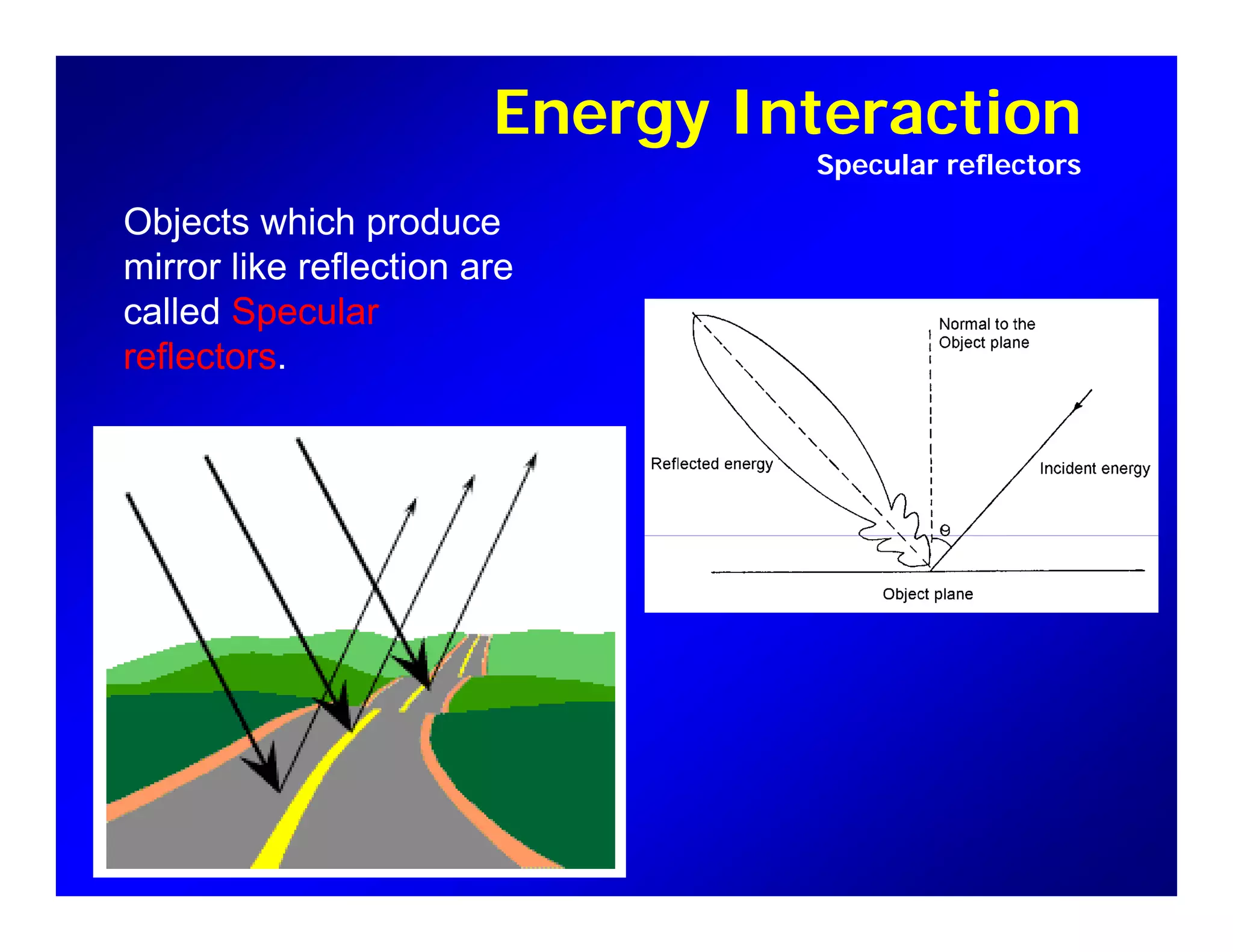
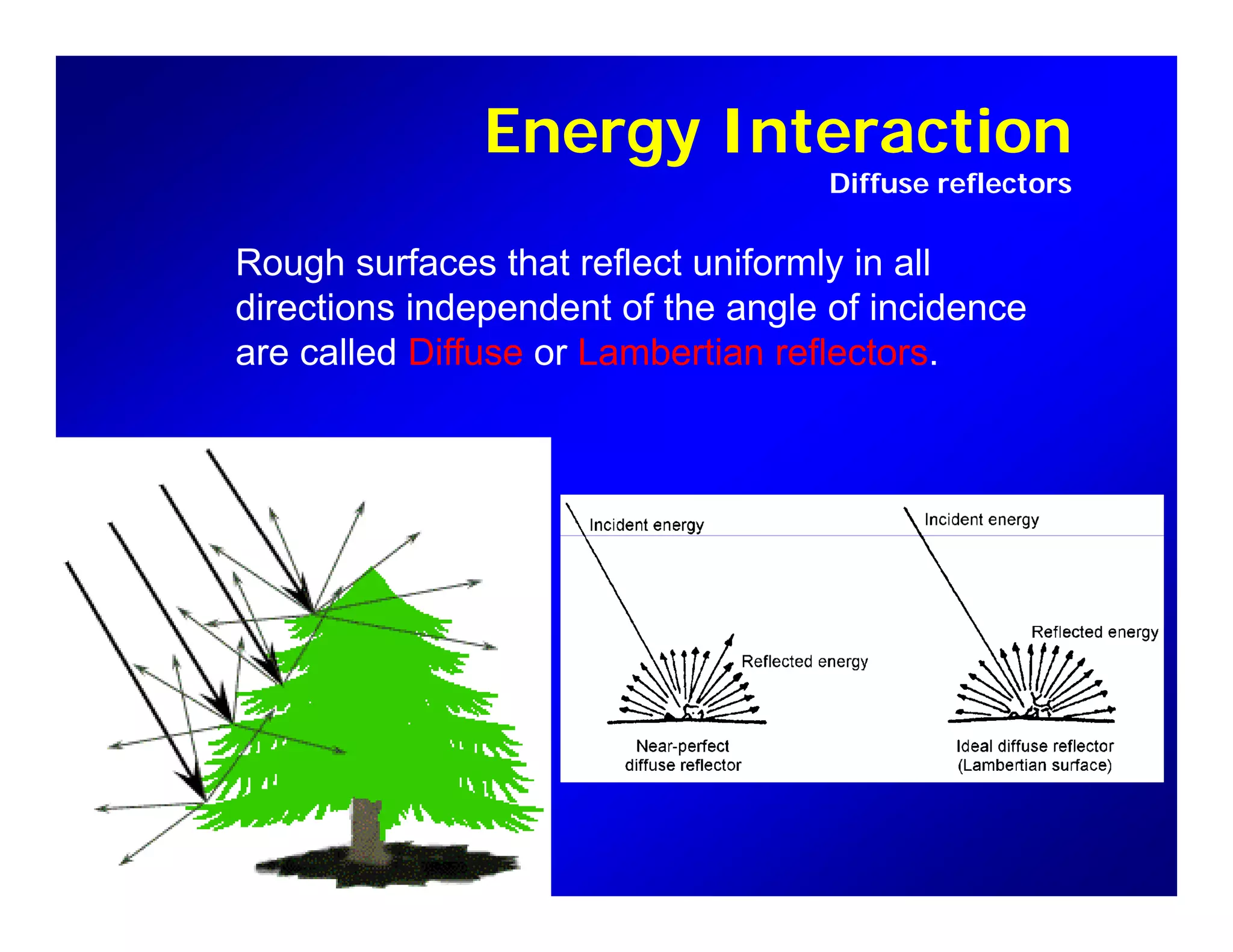
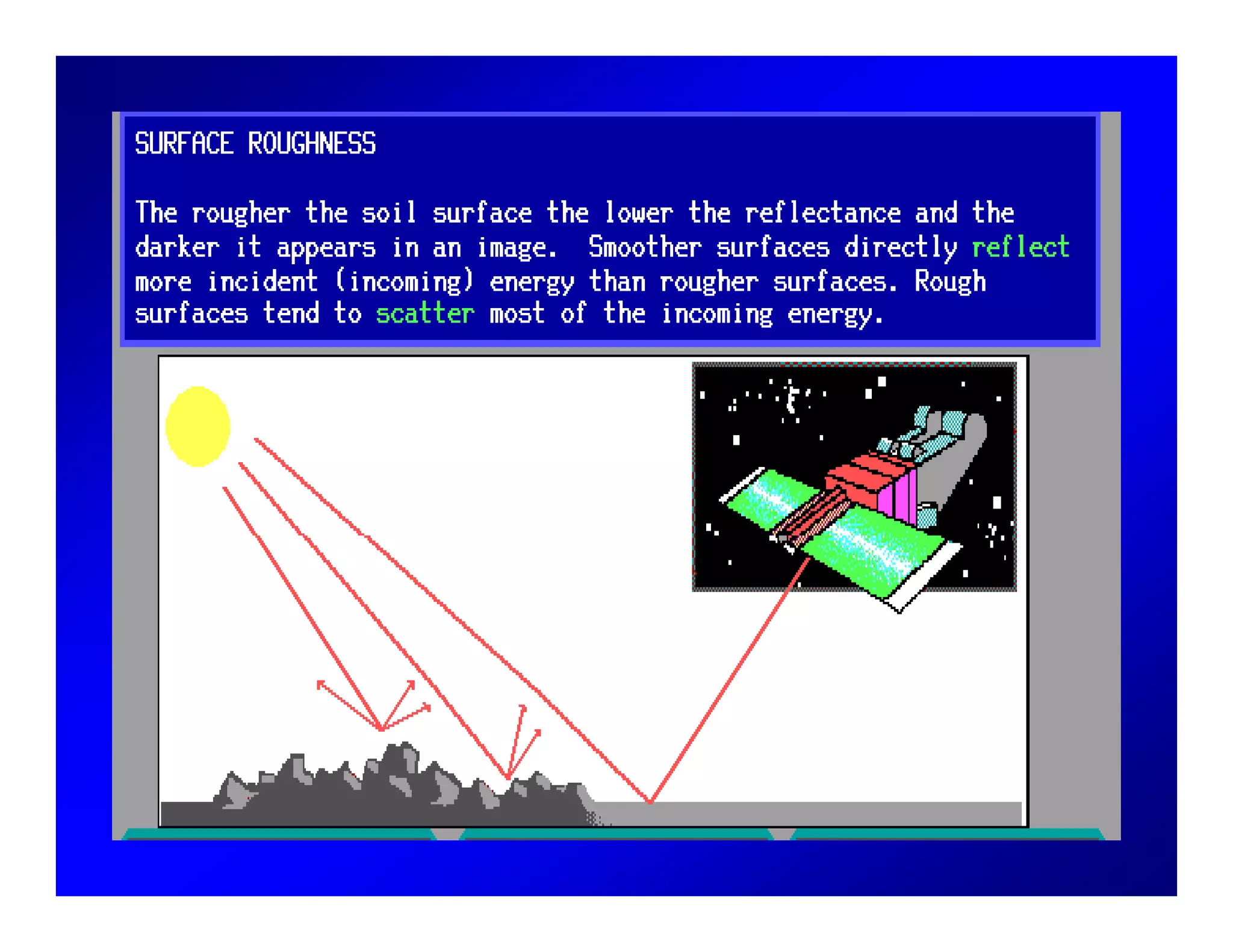
1. The document introduces concepts related to electromagnetic radiation and the electromagnetic spectrum. It discusses how electromagnetic waves are produced by oscillating electric and magnetic fields. 2. Key concepts in remote sensing are introduced such as the electromagnetic spectrum, radiant quantities, energy interactions of reflection, absorption and transmission, and thermal radiation properties. 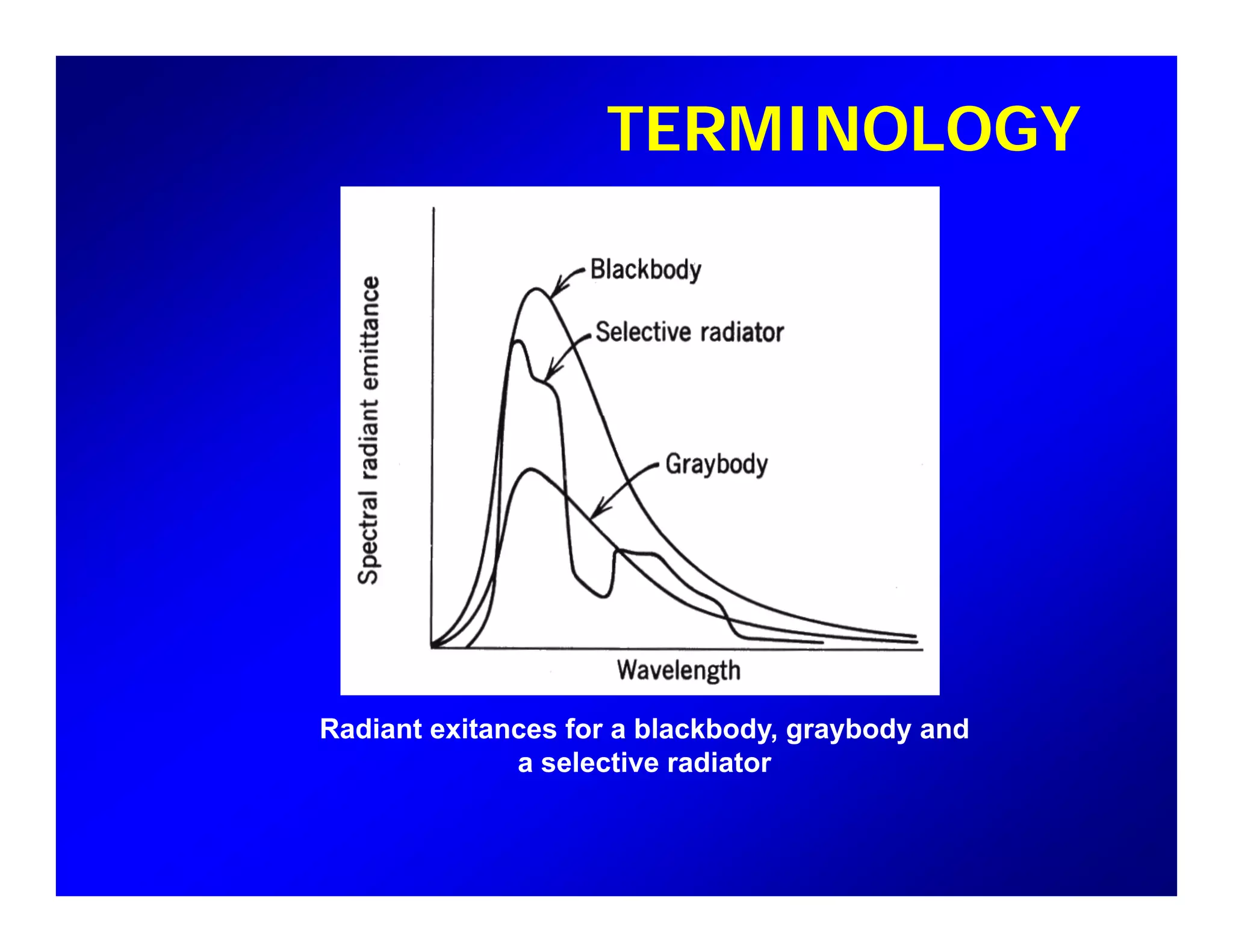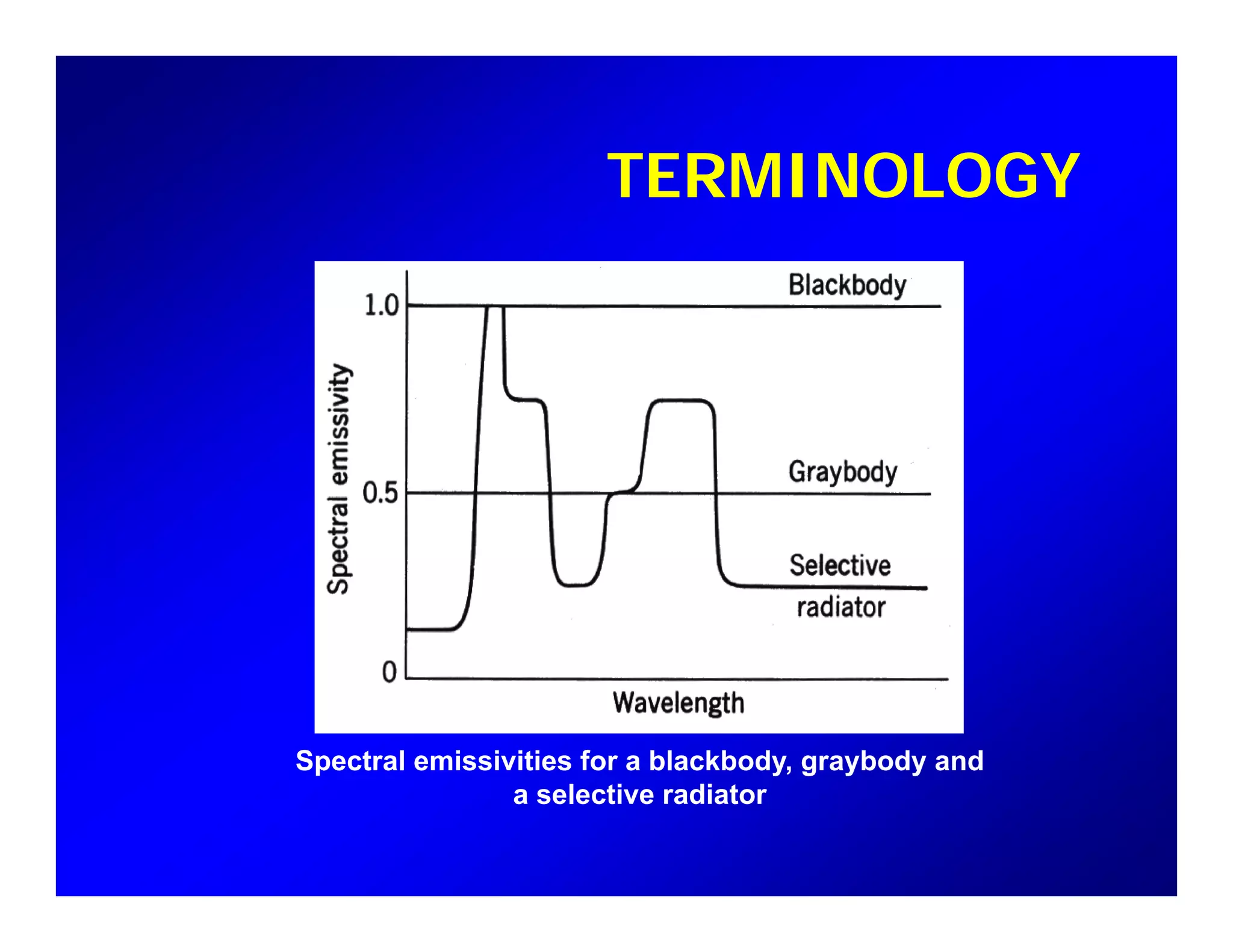3. Principles of thermal remote sensing are covered including Planck's law, Stefan-Boltzmann law, blackbody radiation, emissivity of graybodies and selective radiators, and Wien's displacement law.

1. Introduction toIntroduction to
Physics
fof
Remote Sensing
anjum m@nrsc gov inanjum_m@nrsc.gov.in

2. Electromagnetic Radiation
Motion of charges produces EM waves. Changing Electric fields set
up by oscillation of charged particles. Changing electric fields induce
changing magnetic fields. Changing magnetic fields set up morechanging magnetic fields. Changing magnetic fields set up more
changing fields and so on.

3. Wavelength, Frequency and Amplitude
c = νλ where c = 3 x 108 ms-1
in vacuum

5. THE ELECTROMAGNETIC SPECTRUM

6. Electromagnetic Spectrum
•Violet: 0.4 - 0.446 µm
•Blue: 0.446 - 0.500 µm
•Green: 0.500 - 0.578 µm
•Yellow: 0 578 - 0 592 µmYellow: 0.578 0.592 µm
•Orange: 0.592 - 0.620 µm
•Red: 0.620 - 0.7 µm

7. Microwaves
P band 0.3 – 1 GHz (30 – 100 cm)
L band 1 – 2 GHz (15 – 30 cm)
S band 2 4 GHz (7 5 15 cm)S band 2 – 4 GHz (7.5 – 15 cm)
C band 4 – 8 GHz (3.8 – 7.5 cm)
X band 8 – 12.5 GHz (2.4 – 3.8 cm)
Ku band 12.5 – 18 GHz (1.7 – 2.4 cm)
K band 18 – 26 5 GHz (1 1 – 1 7 cm)K band 18 – 26.5 GHz (1.1 – 1.7 cm)
Ka band 26.5 – 40 GHz (0.75 – 1.1 cm)

9. MotivationMotivation
• Are physical principles important for
application Remote Sensing scientists?pp g
– Why does vegetation reflect more strongly in a
particular wavelength region?p g g
– Is thermal infrared panacea for measurement of
all temperatures?

12. TERMINOLOGY
Radiant energy: Energy carried / transferred by
electromagnetic waves (Joule)e ect o ag et c a es (Jou e)
Radiant energy density: Radiant energy per unit volume
(J/m3)(J/m3)
Radiant flux: Rate at which radiant energy is emitted,
transferred or received in the form of ER. (Watt)
Spectral Radiant flux : Radiant flux per unit wavelengthSpectral Radiant flux : Radiant flux per unit wavelength.
Radiant emittance: Radiant flux emitted per unit area of aRadiant emittance: Radiant flux emitted per unit area of a
source

13. TERMINOLOGYTERMINOLOGY
Radiant Quantities
• Radiant intensity: Radiant flux (power) leaving a source
per unit solid angle in a given direction. (W Sr-1 )
• Irradiance: Radiant flux incident per unit area (W m-2 )
• Radiance: Radiant flux per unit solid angle in a given
direction per unit projected source area in thatp p j
direction. (W m-2 Sr-1 )

14. TERMINOLOGYTERMINOLOGY
Spectral Quantities
• If the previous quantities are measured per unit
wavelength interval at a particular wavelength, then
the quantities are called “spectral quantities”the quantities are called spectral quantities .
Ex: Spectral Radiance (W m-2 sr-1 µm-1)

15. ENERGY INTERACTION
Wh EM i i id t i
ENERGY INTERACTION
Conservation of Energy
When EM energy is incident on any given
earth surface feature, three fundamental
energy interactions are possible. A fraction ofgy p
incident energy is reflected, absorbed and / or
transmitted.
“Energy is neither created nor destroyed.”
Incident energy = reflected energyIncident energy reflected energy
+
transmitted energy
+
b b dabsorbed energy

16. Three forms of interaction
I=A+R+T or A/I+R/I+T/I=1 (100%)

17. Energy InteractionEnergy Interaction
Conservation of Energy
T i t b t th ti f l ti hiTwo points about the conservation of energy relationship:
• The proportions of energy reflected,absorbed and
transmitted will vary for different earth features
depending on their material type and condition.
• The wavelength dependency. That is, even within a
given feature type the proportion of reflected absorbedgiven feature type, the proportion of reflected, absorbed
and transmitted energy will vary at different
wavelengths.
Two features may be distinguishable in one spectral range
but not in another wavelength region.

18. Energy InteractionEnergy Interaction
Reflection
Many remote sensing systems operate in
visible and NIR regions in which reflected
energy is more Hence the reflectanceenergy is more. Hence, the reflectance
properties of objects are more important.
The reflectance is a function of surfaceThe reflectance is a function of surface
roughness (or smoothness) of object.
Based on surface roughness objects areg j
categorized into two classes.

19. Energy Interaction
Specular reflectorsp
Objects which produce
mirror like reflection are
called Specular
reflectors.

20. Energy Interaction
Diff fl tDiffuse reflectors
Rough surfaces that reflect uniformly in all
di ti i d d t f th l f i iddirections independent of the angle of incidence
are called Diffuse or Lambertian reflectors.

22. Energy InteractionEnergy Interaction
Smooth and Rough
Smoothness or roughness of a surface
depends on the wavelength of the incident
di ti d id tiradiation under consideration.
According to Rayleigh, a surface is smooth
if the surface height variations are less thanif the surface height variations are less than
λ/8, where λ is the wavelength of incident
radiation. Otherwise, surface is considered
to be rough.

23. TERMINOLOGY
Ratio Quantities
Emissivity: Ratio of radiant emittance of a source
to that a blackbody at the same temperaturey p
Reflectance: Ratio of reflected radiant flux to
incident radiant flux
Absorptance: Ratio of absorbed radiant flux to
incident radiant flux
Transmittance: Ratio of transmitted radiant flux
to incident radiant flux

24. Types of Remote Sensing SensorsTypes of Remote Sensing Sensors
Active
Passive

25. Introduction to Principles ofp
thermal Remote Sensing

26. Thermal Radiation
Any object above absolute zero, emits EMR. Objects around
and we ourselves are thermal radiators.
Ideal thermal radiator – Black body.
Emission is according to the Planck’s lawEmission is according to the Planck s law
M(λ)= C1λ-5/[exp(C2/λT) - 1]

27. Planck’s lawPlanck s law
Planck’s Law: The most general lawPlanck s Law: The most general law
Planck's Law allows us to calculate total energy
di t d i ll di ti f bl kb dradiated in all directions from a blackbody
(radiator) for a particular temperature and
wavelength.g
M(λ)= C1λ-5/[exp(C2/λT) - 1]
hwhere
C1(2πhc2) = 3.74 x 10-16 W m-2, C2 (hc/k)= 1.44 x 10-2 m °K,
λ = wavelength (µm), T = temperature (°K),
M(λ) = spectral exitance (W m-2 µm-1)M(λ) = spectral exitance (W m µm ),
k = 1.38 x 10-23 W s K-1, h = 6.625 x 10-34 J s

28. TERMINOLOGY
Blackbody
An ideal thermal emitter is called a Blackbody. (Also
known as Planckian radiator.) A black body is an ideal
f h th tsurface such that
•Its emissivity is equal to 1. In other words it radiates
the entire energy whatever it absorbedthe entire energy whatever it absorbed.
•For a given temp and wavelength, no body can emit
more energy than a black bodymore energy than a black body.
• Emission from a black body is independent of
direction, i.e. it is a diffuse emitter.d ect o , e t s a d use e tte

29. RADIATION LAWSRADIATION LAWS
Stefan-Boltzmann Law
The total energy radiated by an object at
a particular temperature is given by
M = σ T4
where M is total radiant exitance from the surface of the
material (W m-2), σ is Stefan-Boltzmann constant (5.67 x 10-8
W m-2 °K-4),
T is absolute temperature in °KT is absolute temperature in K.
The higher the temperature of the radiator, the greater the
total amount of radiation it emits

30. RADIATION LAWS
It is continuous.
Single maximum for any temp
A T i hift tAs T increase, max shifts to
the shorter wavelength.
Exitance value is higher than
That for the lesser T.
Curves do not intersect.
Beyond max radiationBeyond max, radiation
Decrease monotonically with
Increasing wavlength.
I h t i ti di tiImp characteristic – radiation
Even in microwave region.
Spectral distribution of energy
radiated by blackbodies at
various temperatures
9.6 µm

31. Blackbody Radiation
• A blackbody is a perfect emitter and
absorber of EM radiation.
• Two laws explaining the emission
characteristics of the body are:characteristics of the body are:
(a) Wein’s law
(b) R l i h J l(b) Rayleigh-Jeans law

32. Wein’s law
Thi l h ld d f hi h f i• This law holds good for high frequencies
M(λ)=C1λ-5/exp(C2/λT)
M is the spectral Exitance
With C1 and C2 as constantsWith C1 and C2 as constants
Gives the wavelength at which the
exitance is maximum and is related toexitance is maximum and is related to
temperature.
λ T constant• λ maxT = constant
If λ max is in micrometer and T in 0K, the
constt= 2897
λ max = 2897/T

33. For Earth T 300 0KFor Earth, T ~ 300 0K
λ = 9 66 micronλ max = 9.66 micron.
Hence 8 15 micrometer region thermal IR regionHence 8 – 15 micrometer region – thermal IR region

34. TERMINOLOGY
Graybody
A graybody is one for which emissivity
value is constant but less than unity.
A l ti di t i f hi hA selective radiator is one for which
emissivity value varies with wavelength.

35. TERMINOLOGY
Radiant exitances for a blackbody, graybody and
a selective radiator

36. TERMINOLOGYTERMINOLOGY
Spectral emissivities for a blackbody, graybody andp y g y y
a selective radiator

37. l h lRayleigh-Jeans law
• This law explains blackbody emission at
high wavelengths:g g
• M(λ)=C λ-4T/C• M(λ)=C1λ 4T/C2

38. PARTICLE THEORY
The particle theory suggests that electromagnetic
radiation is composed of many discrete packets
f ll d “Ph t ” “Q t ”of energy called “Photons” or “Quanta”.
The energy of each quantum is given by
Q = hν
where Q is energy of quantum (J), h is Planck’s constant (6.626 x
10-34 J-s) and ν is frequency
Also, Q = hc/λ, implies the longer the wavelength involved, the lower its
energy content.

39. RELEVANCERELEVANCE
Wien’s Displacement Law
• Is Thermal Infrared suitable for measurements• Is Thermal Infrared suitable for measurements
of all ranges of temperatures? ---- NO!
• Glacier at –20 °C (~253 K): λm =2898/253=11.45
µm (TIR)
• Room Temperature (300 K): λm =2898/300=9.66
µm (TIR)
• Forest fire (~800K): λm =2898/800=3.66 µm (TIR)m µ
• Volcano (~1200 °C): λm =2898/1473=1.97 µm
(Mid IR)
• Sun (6000 K): λm =2898/6000=0.48 µm (Green)Su (6000 ) λm 898/6000 0 48 µ (G ee )

40. ConclusionsConclusions
• In remote sensing, we study
reflective/emissive/scattered properties
F ifi l d diff• For a specific target, specular and diffuse
interactions depend on the incoming
wavelengthwavelength
• In thermal remote sensing, emission is the
key and thermal (far) infrared is not always
the answer
• Physical principles are important for
understanding processes in remote sensing!understanding processes in remote sensing!