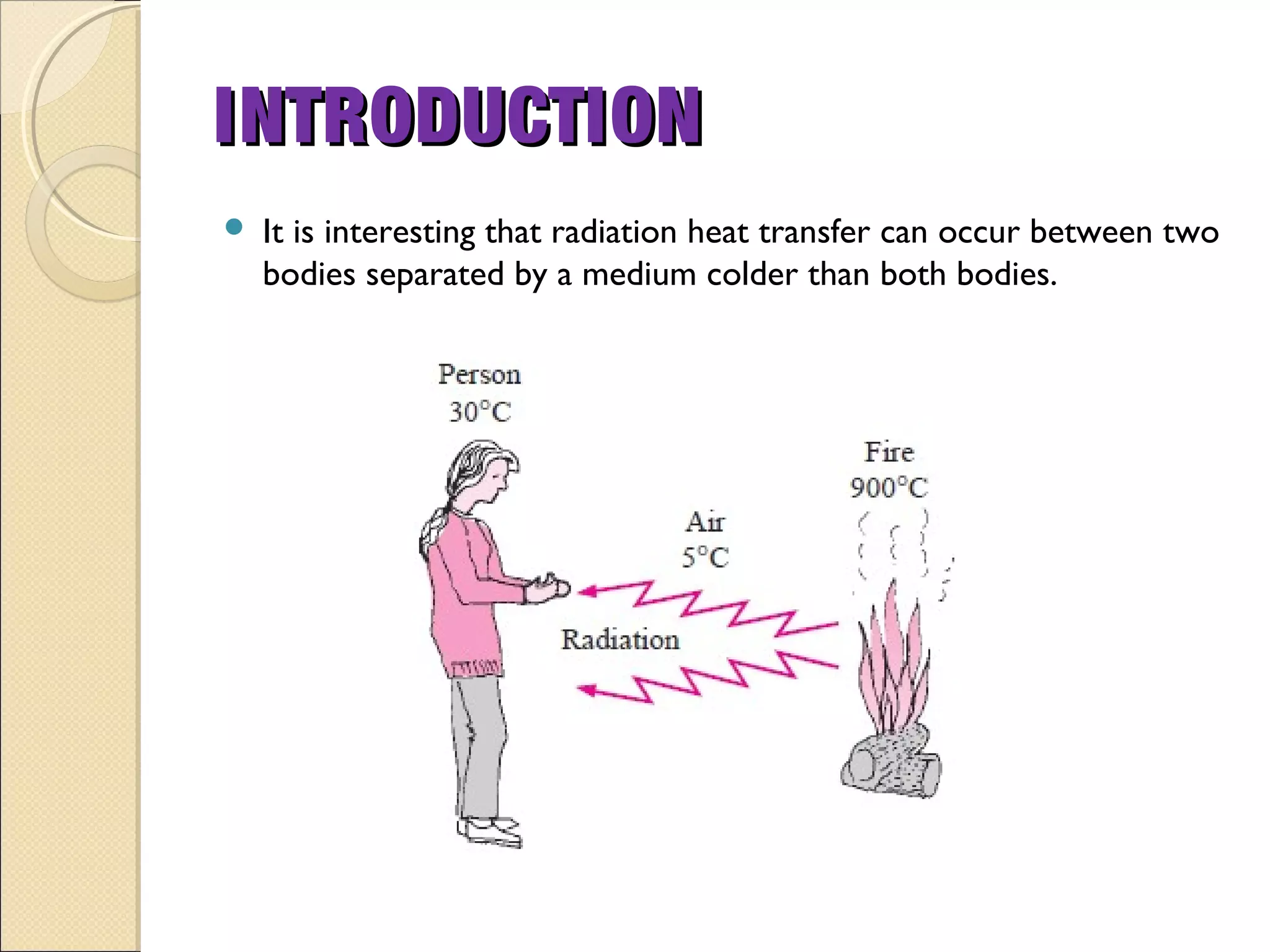
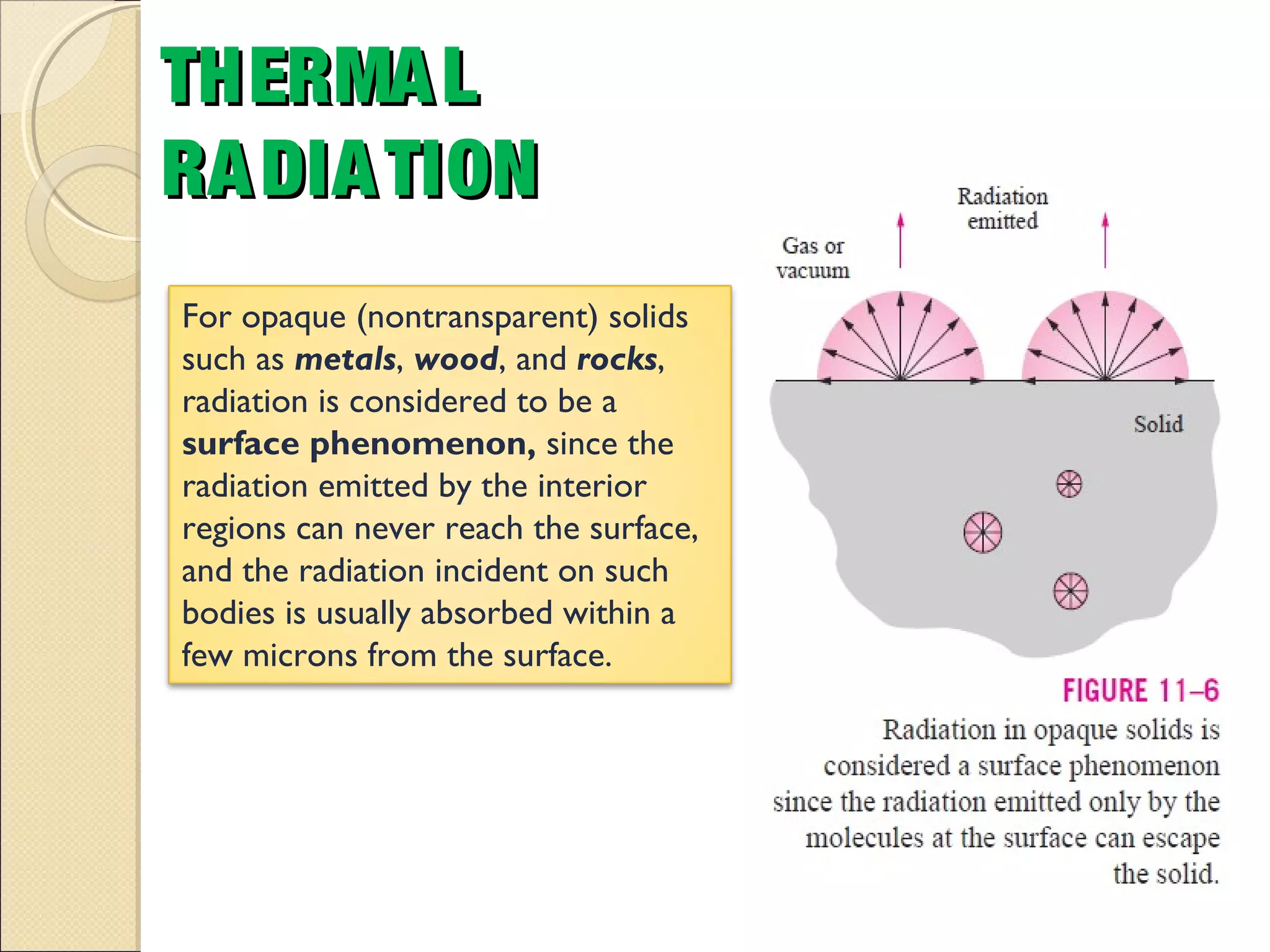
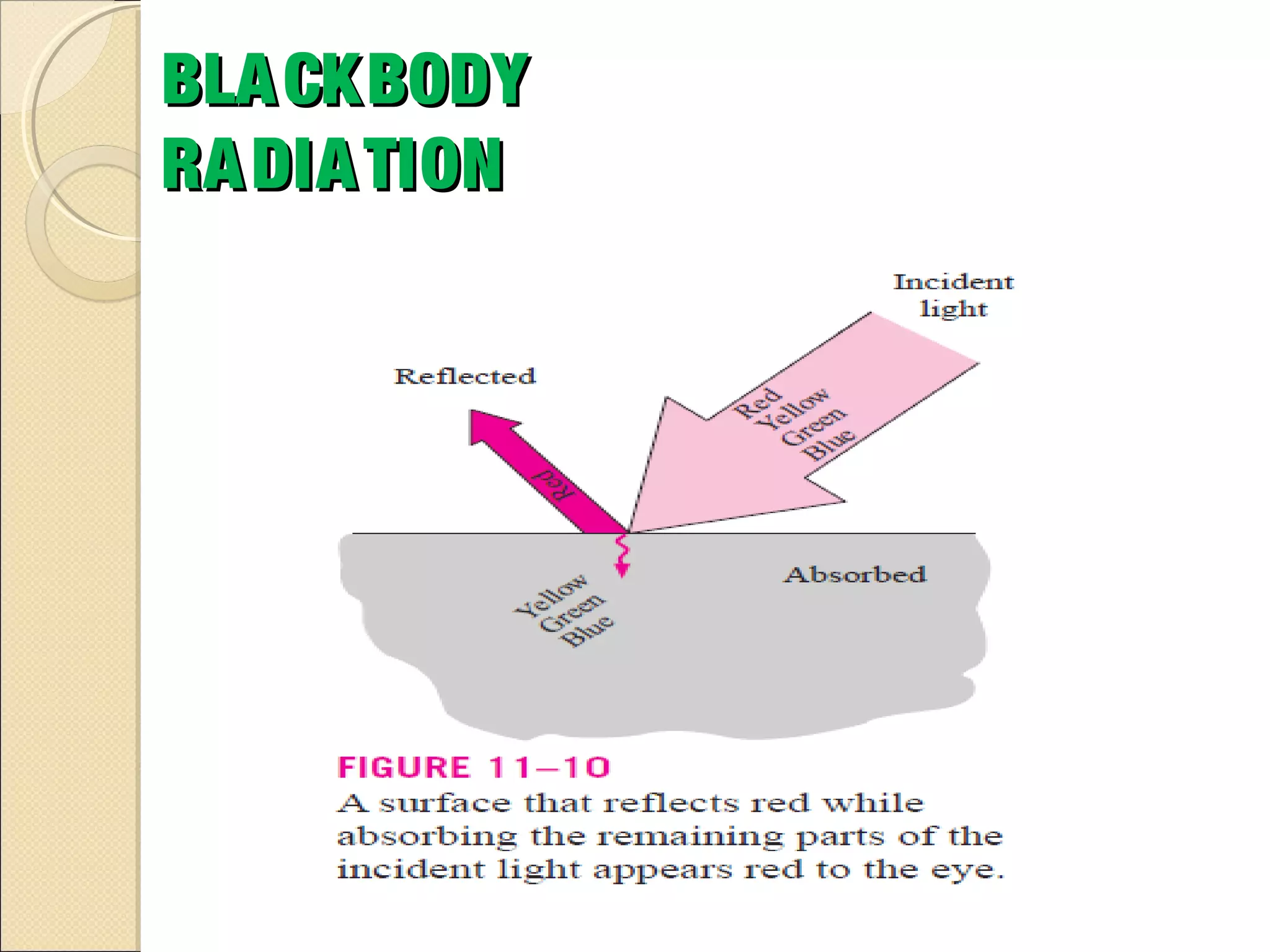
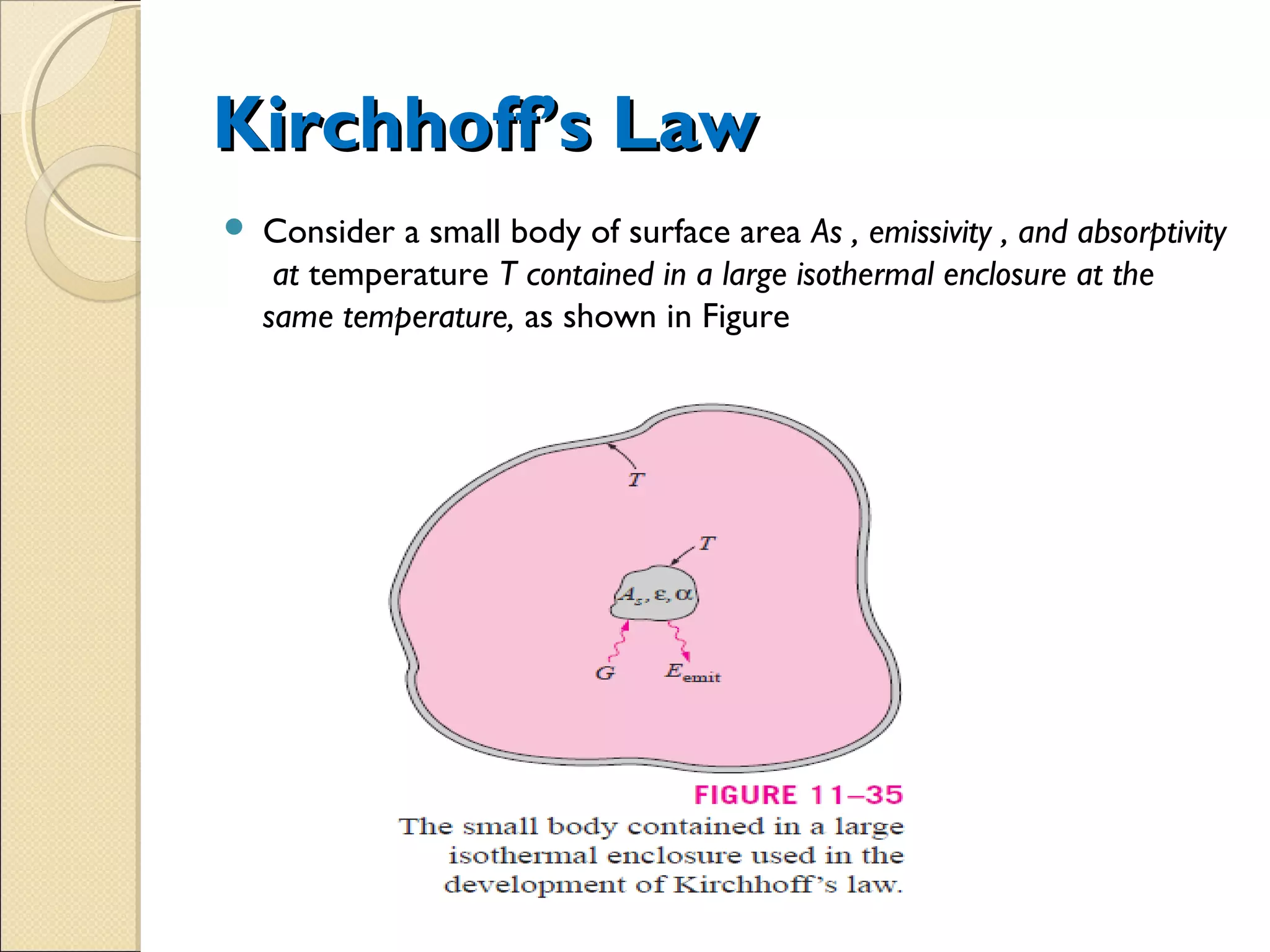
- Thermal radiation is electromagnetic radiation emitted from objects due to their temperature. It includes infrared, visible light, and some ultraviolet wavelengths. A blackbody is a perfect emitter and absorber of radiation. According to Stefan-Boltzmann law, a blackbody's total emissive power is directly proportional to the fourth power of its absolute temperature. Planck's law describes the spectral distribution of a blackbody's radiative intensity as a function of wavelength and temperature. The emissivity of a surface is the ratio of radiation it emits compared to a blackbody. Kirchhoff's law states that emissivity of a surface is equal to its absorptivity at a given temperature and wavelength. The greenhouse effect