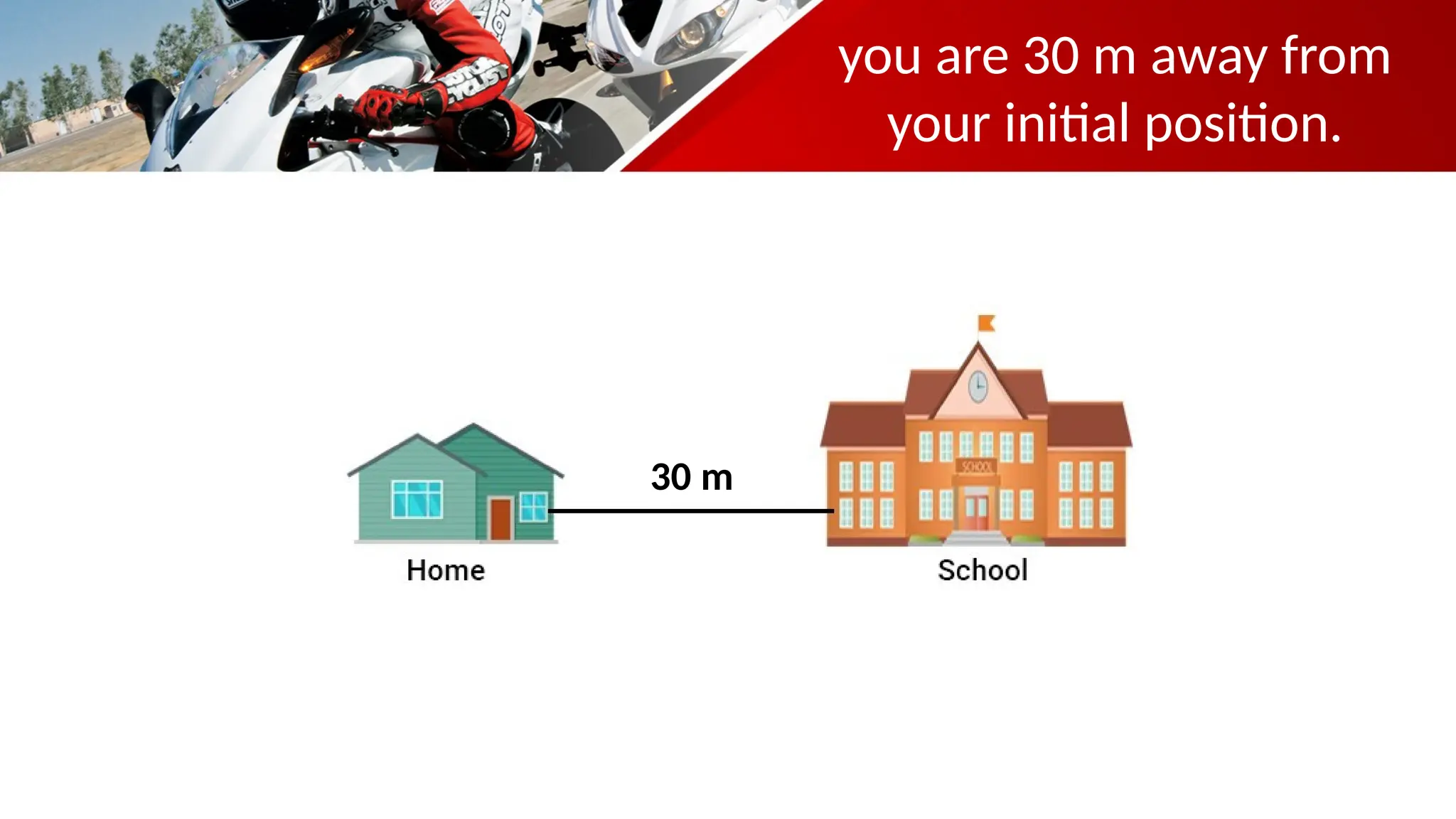
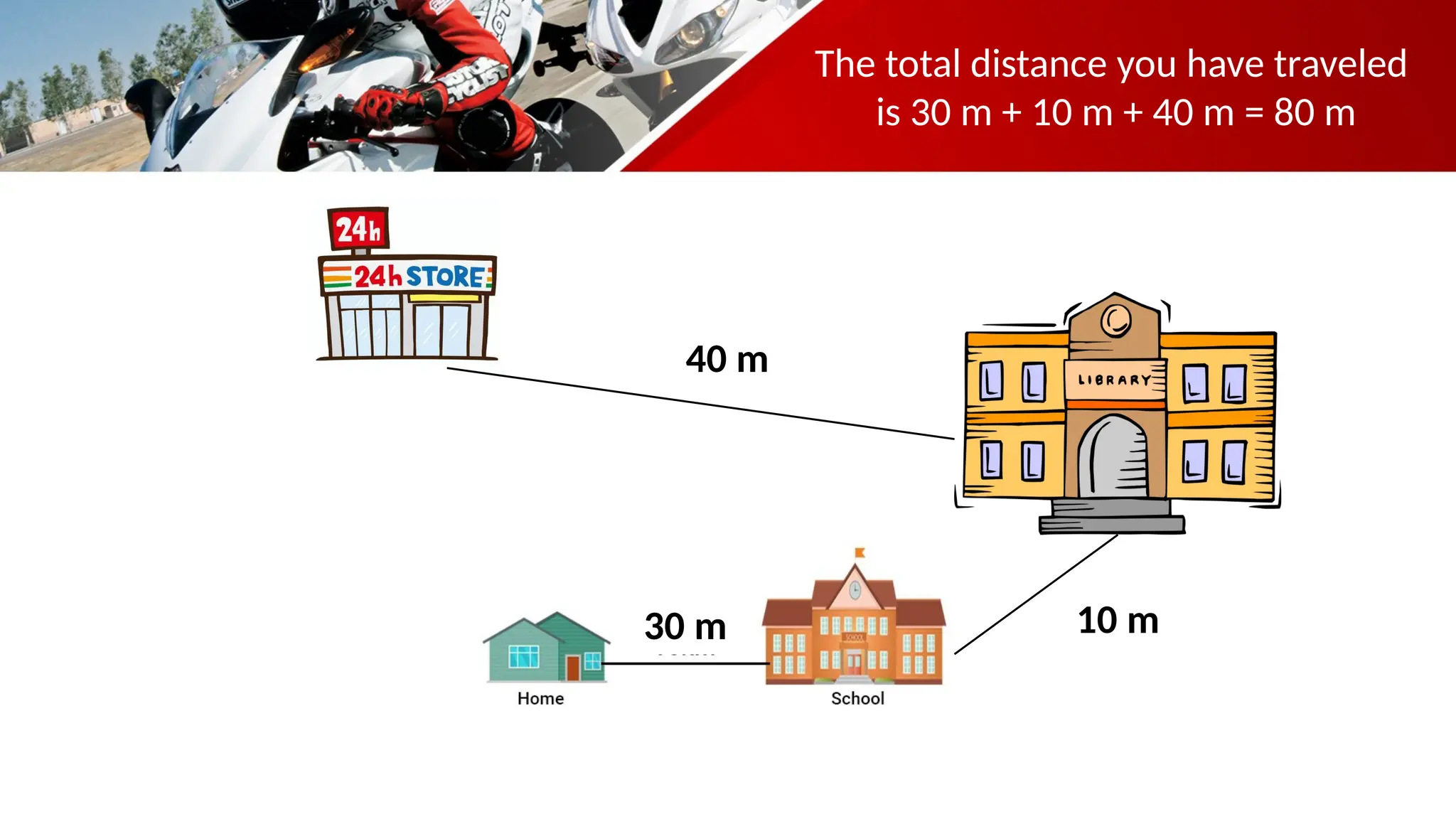
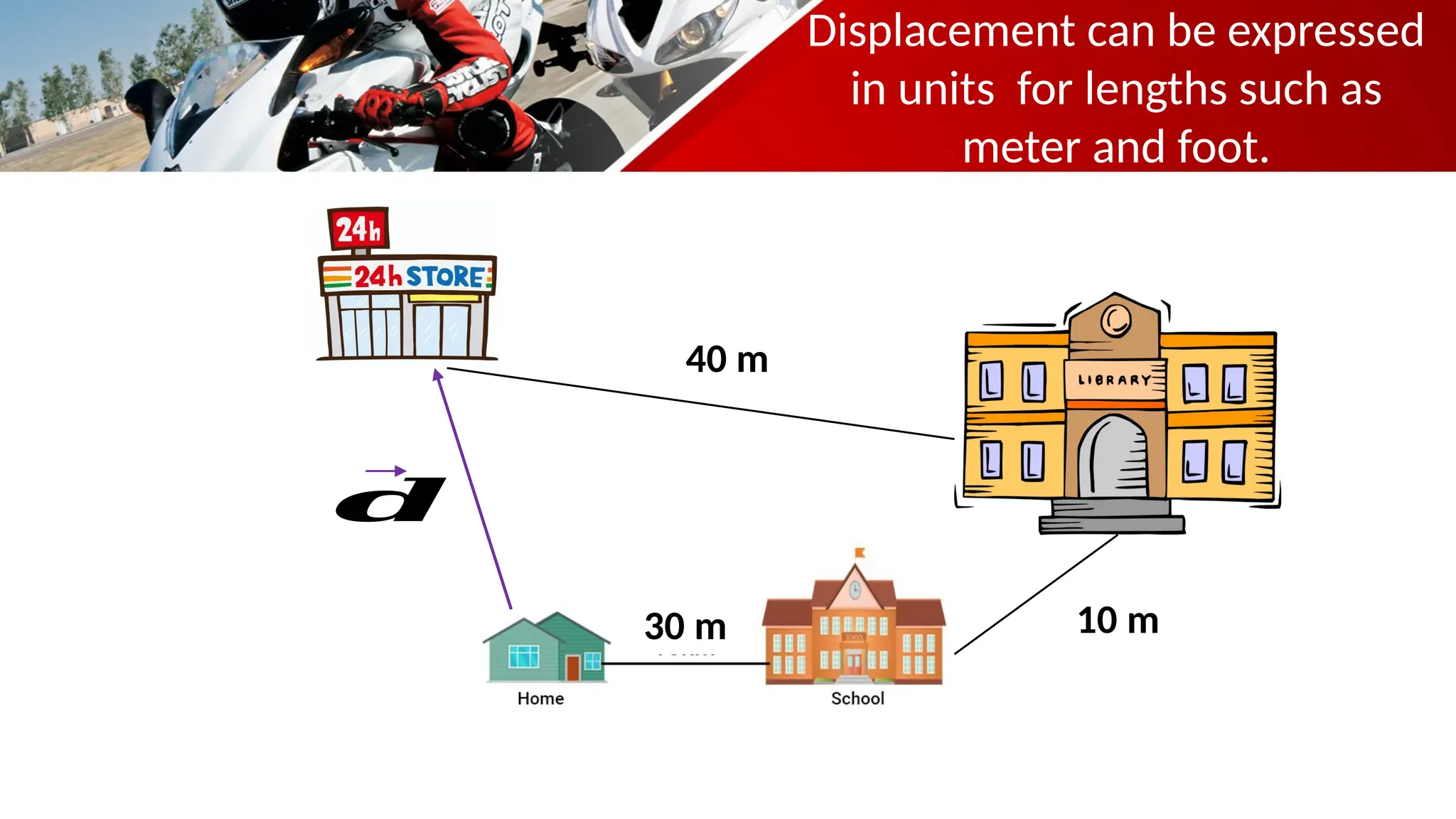
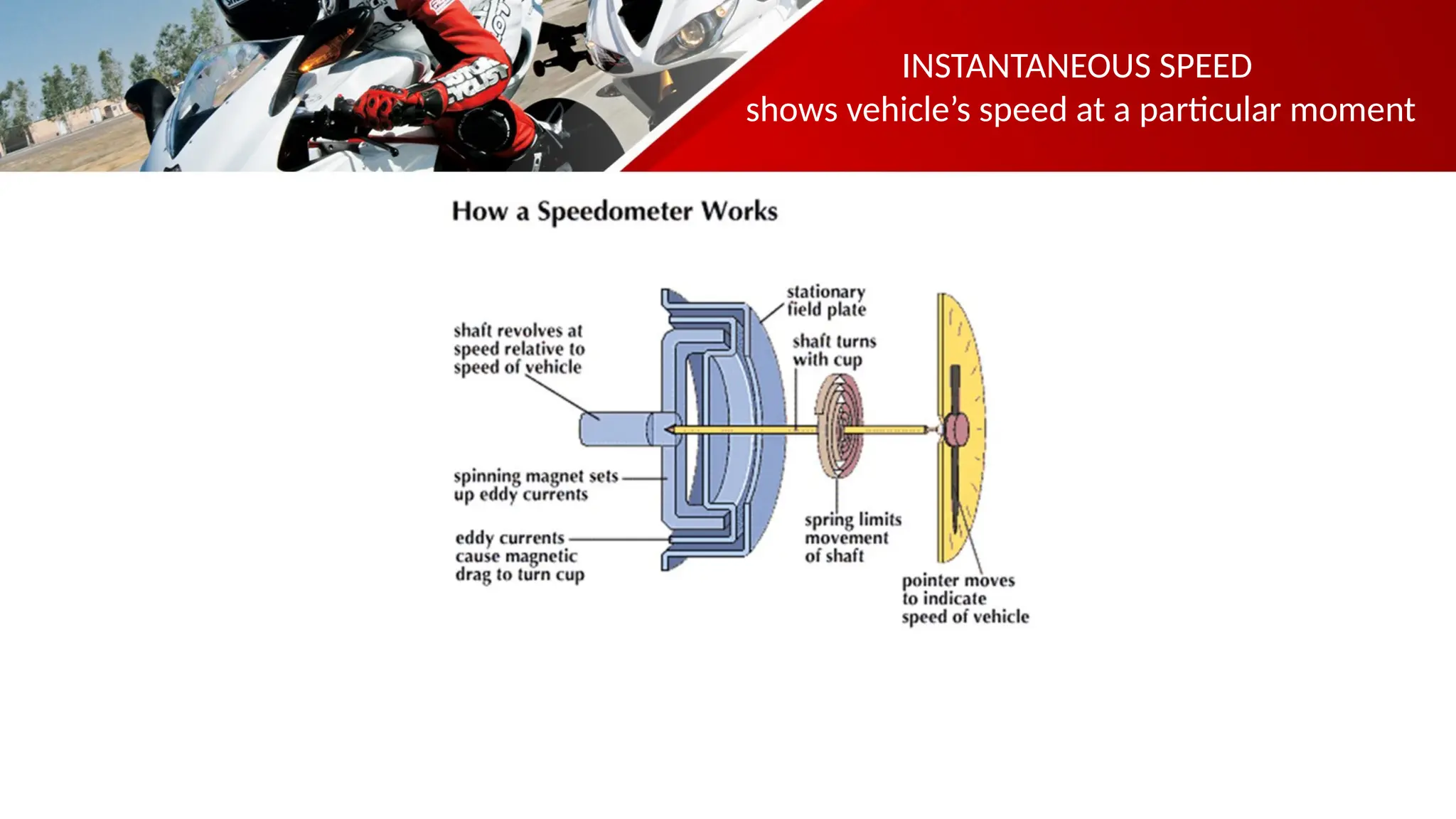
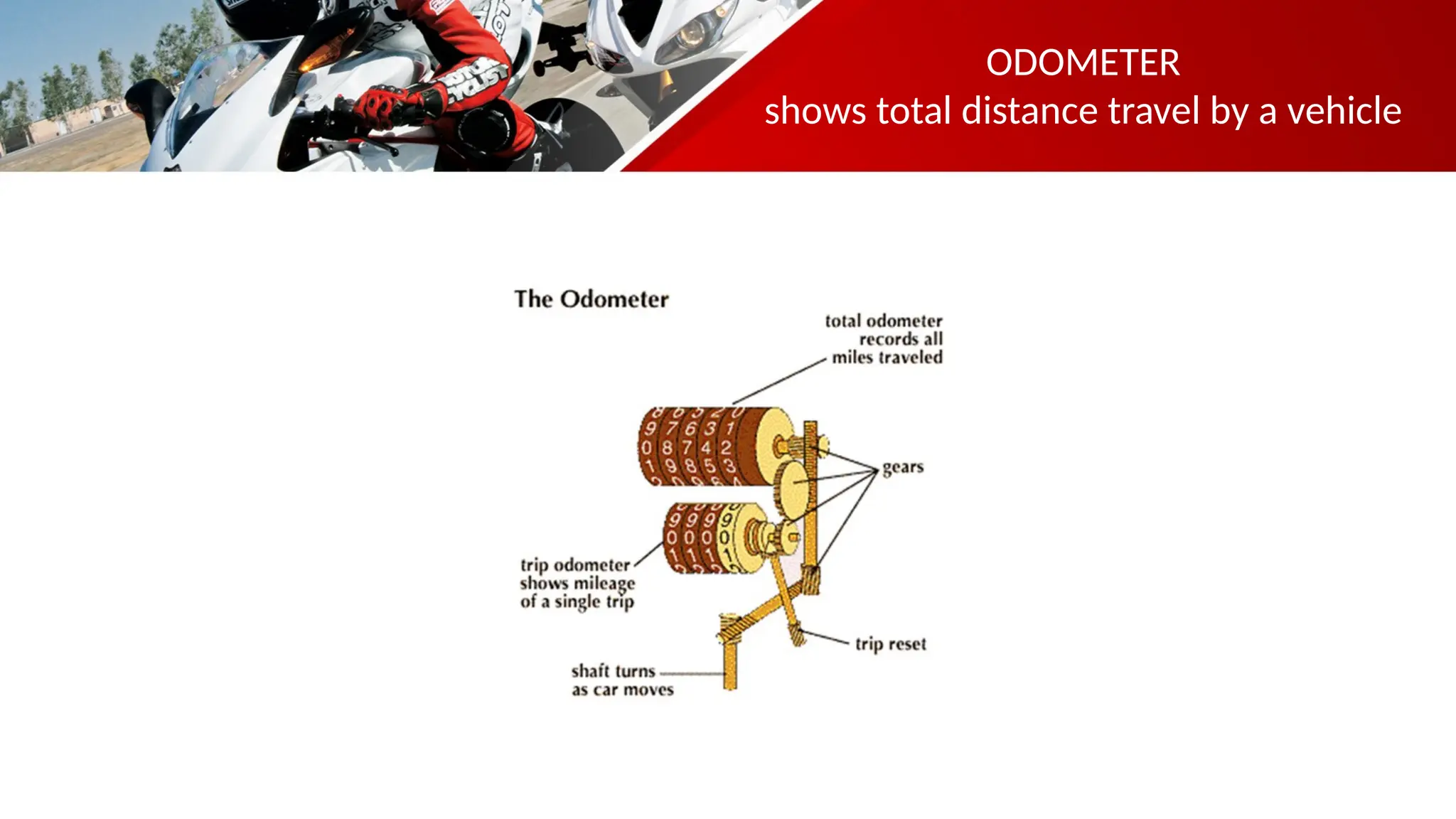
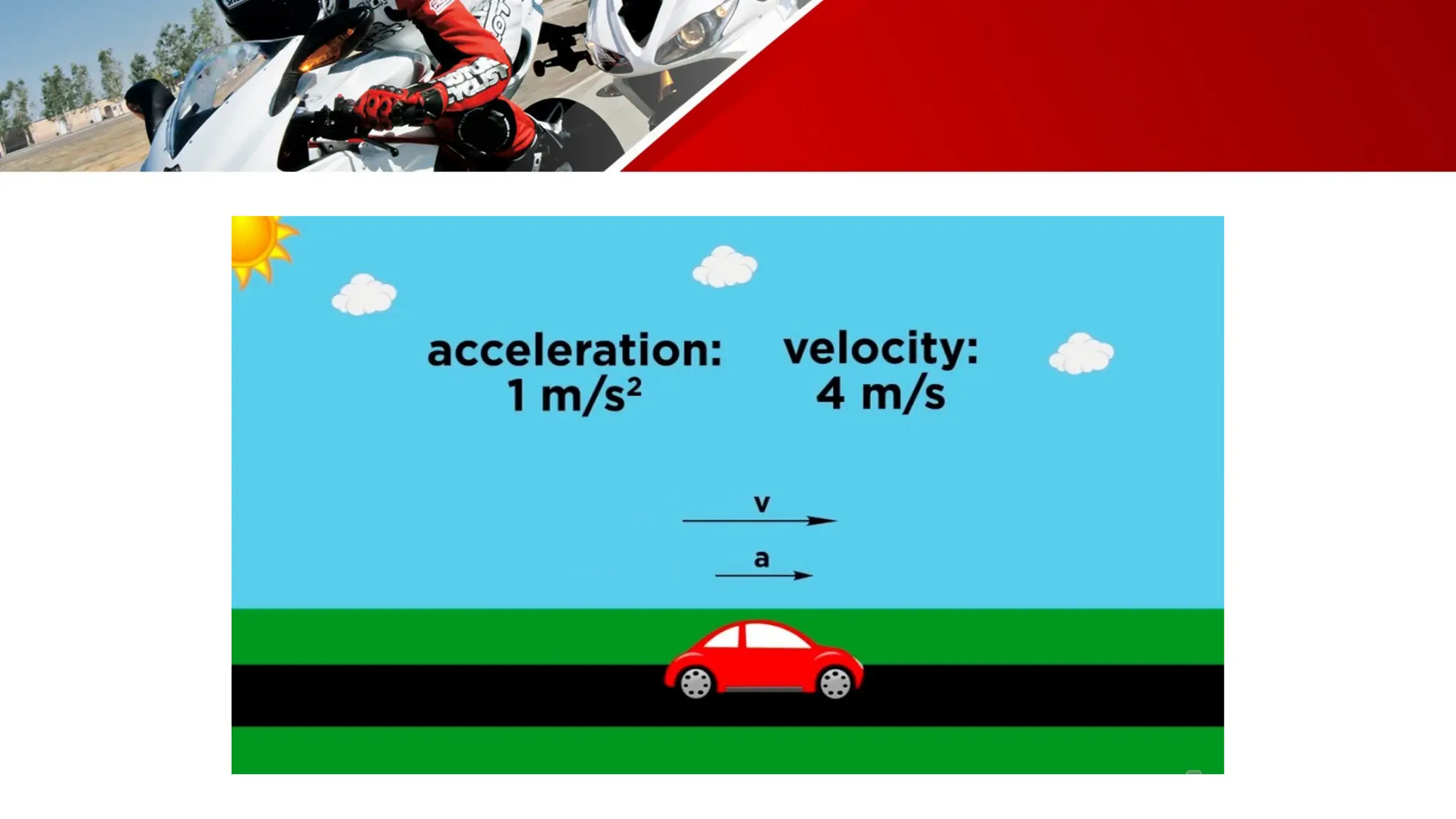
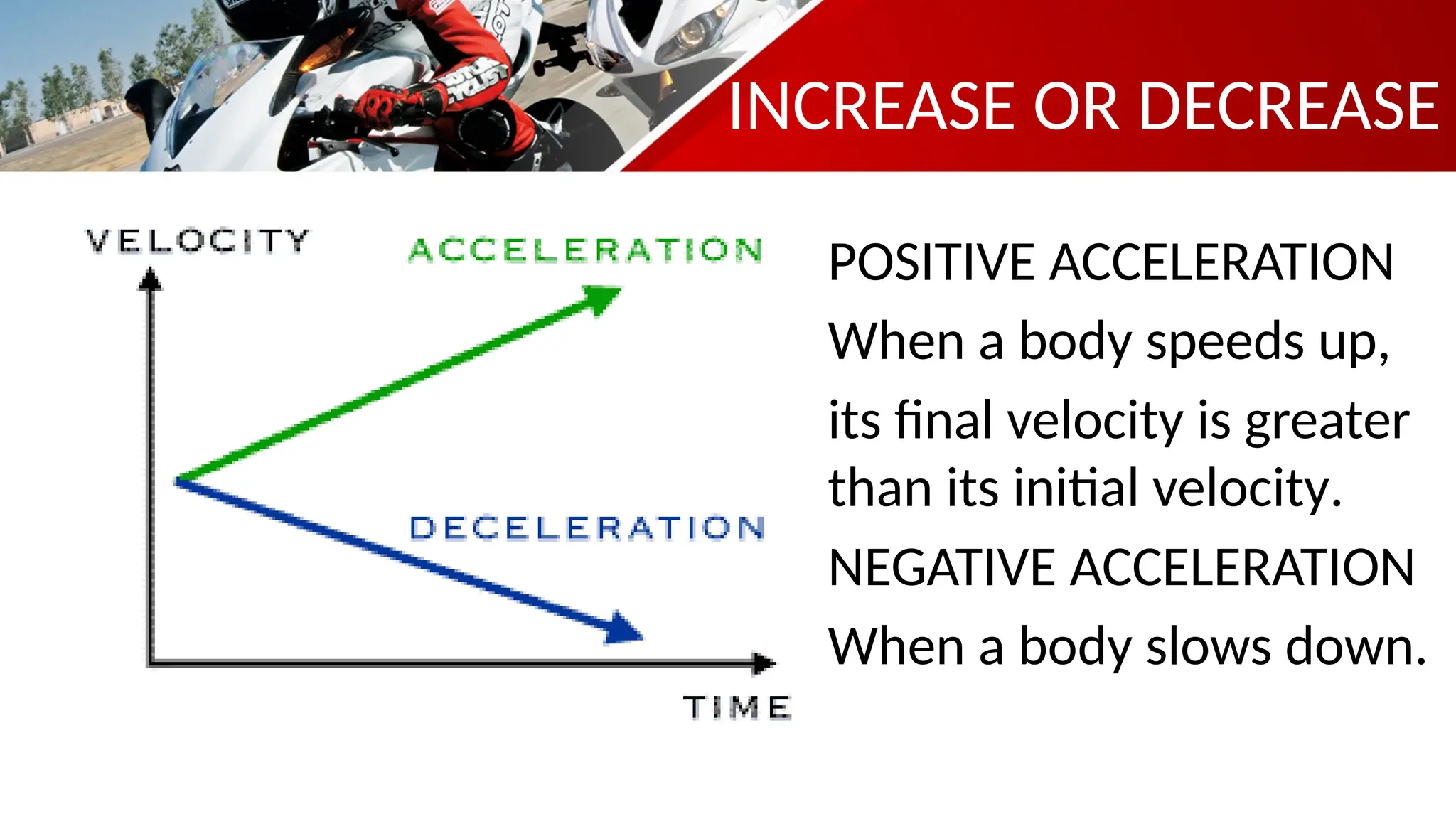
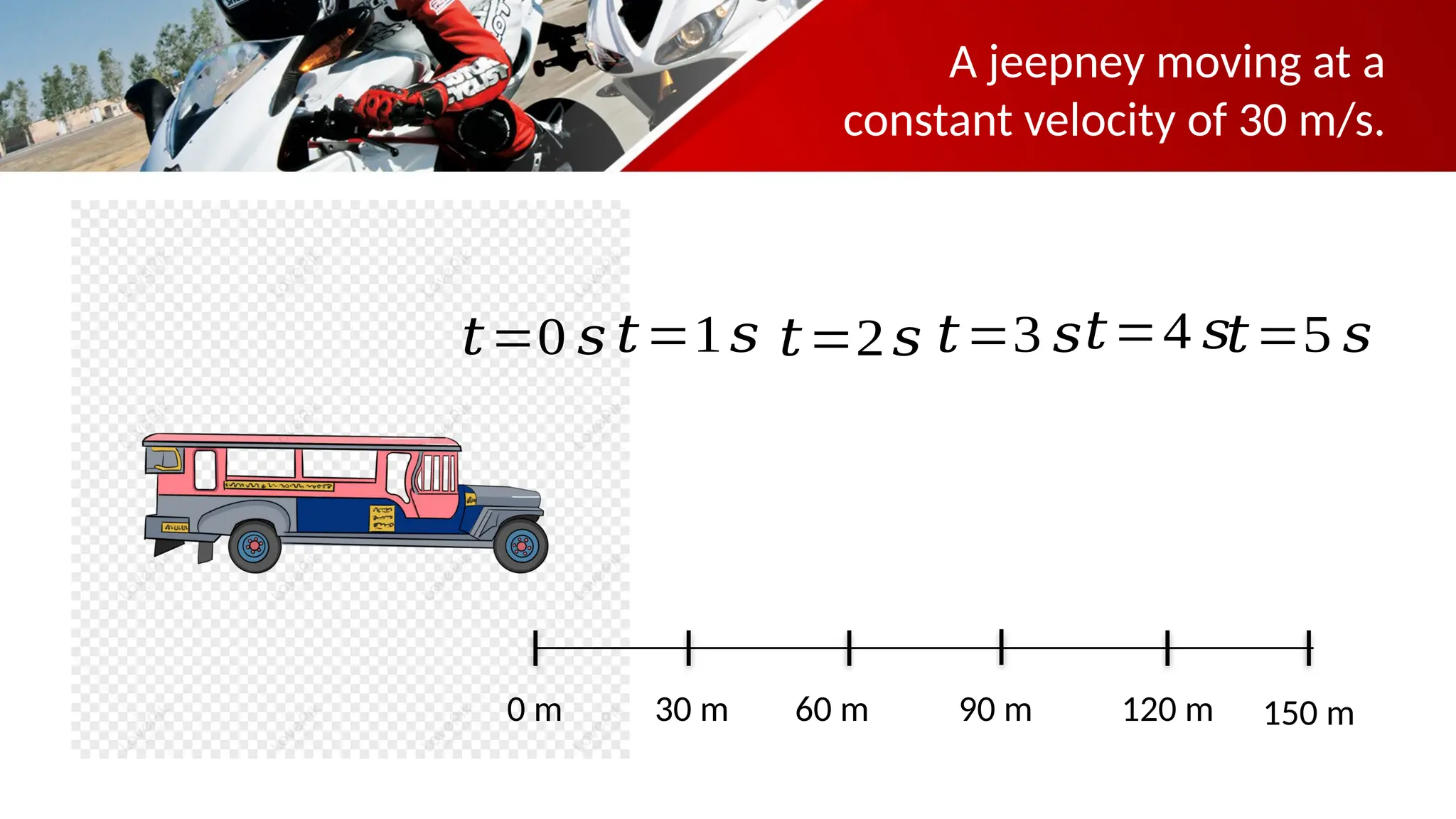
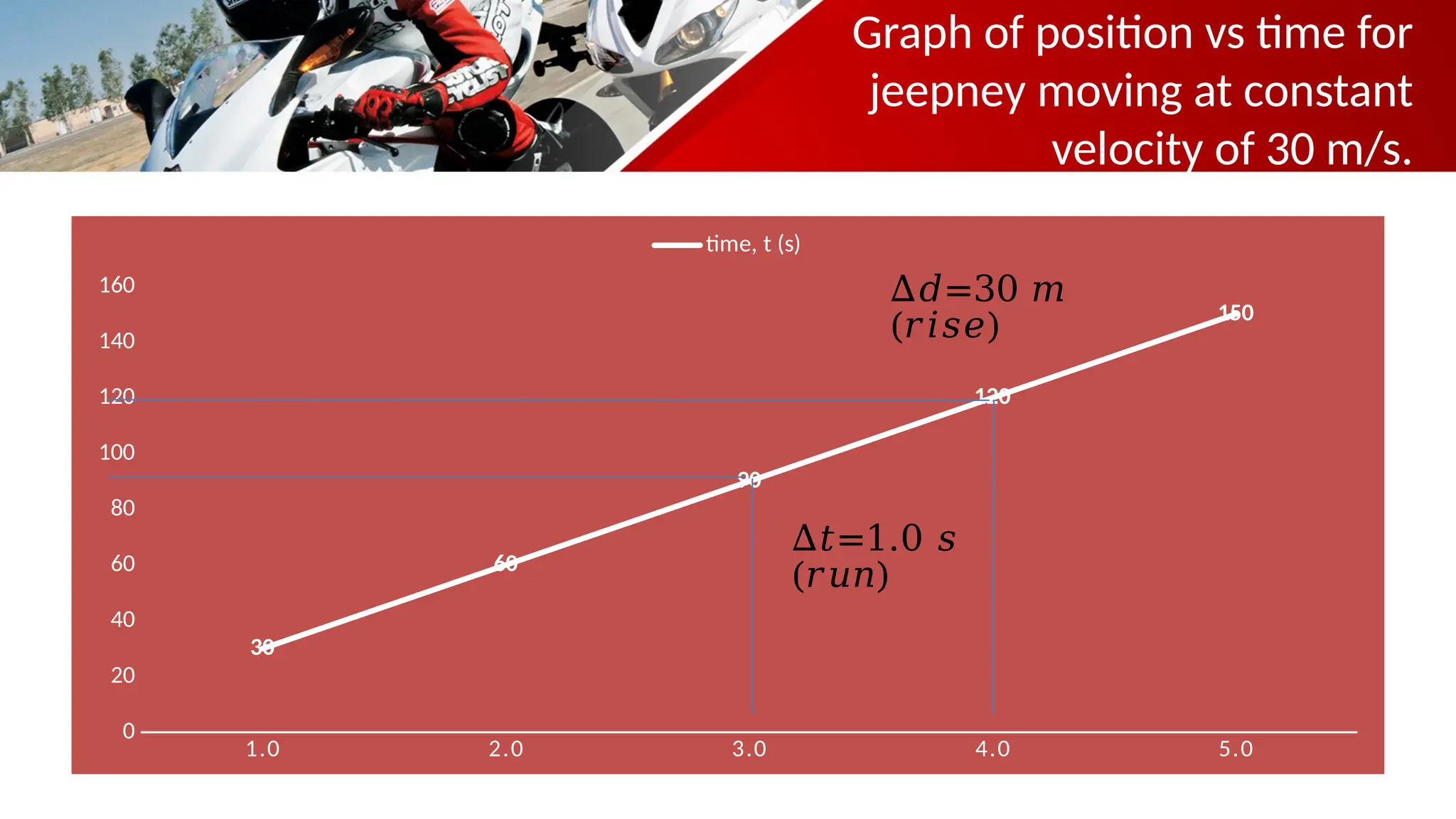
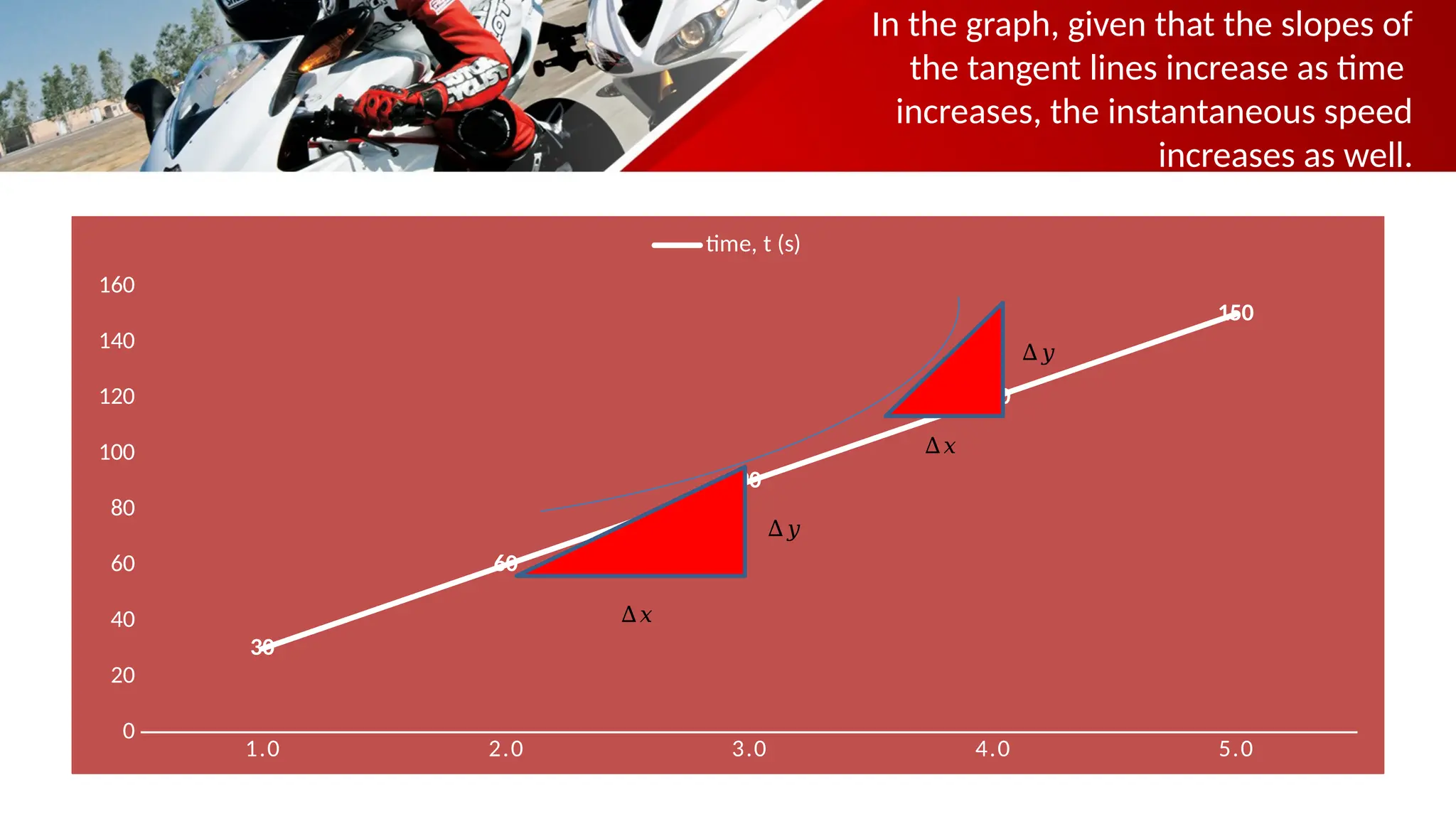
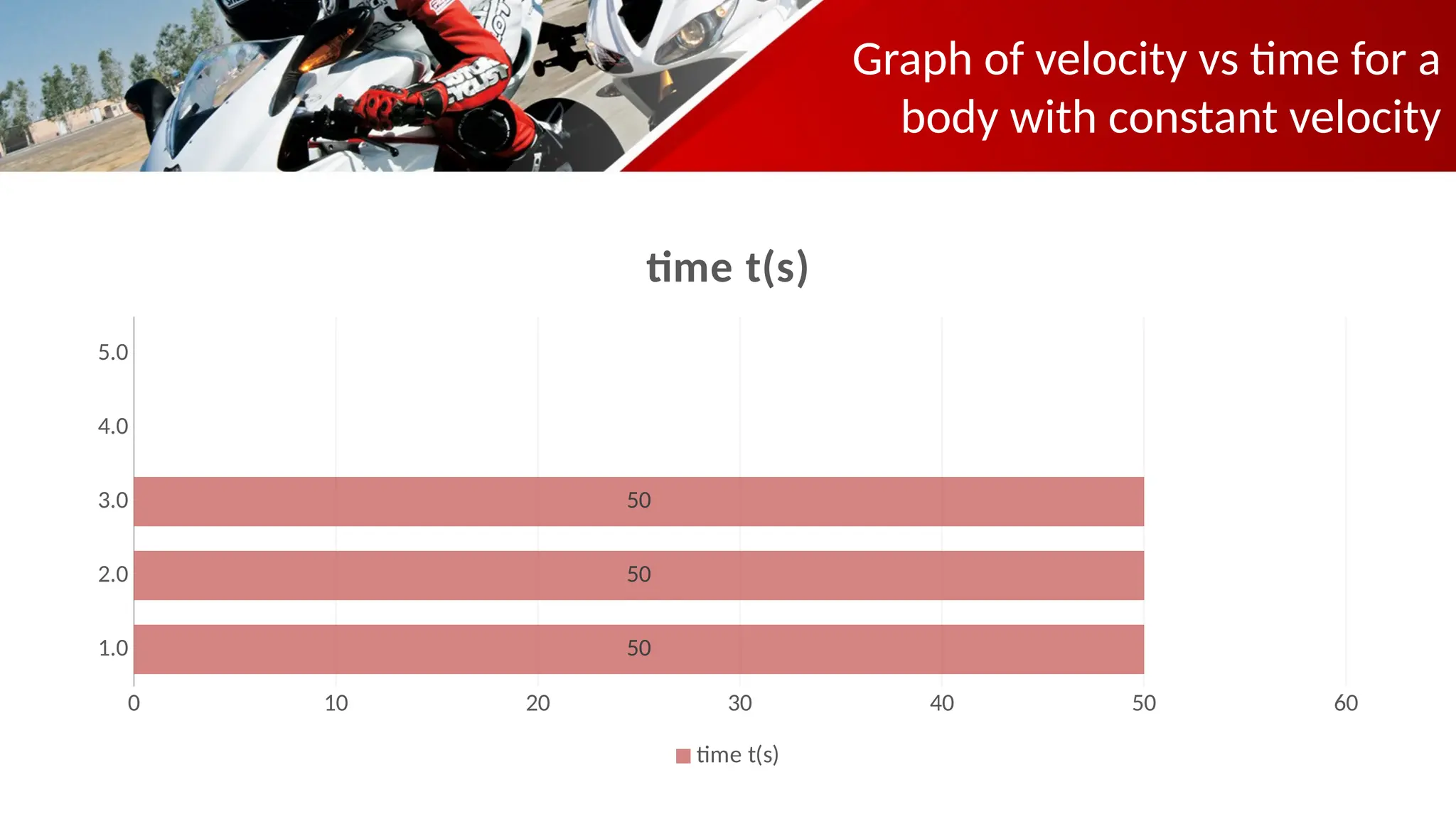
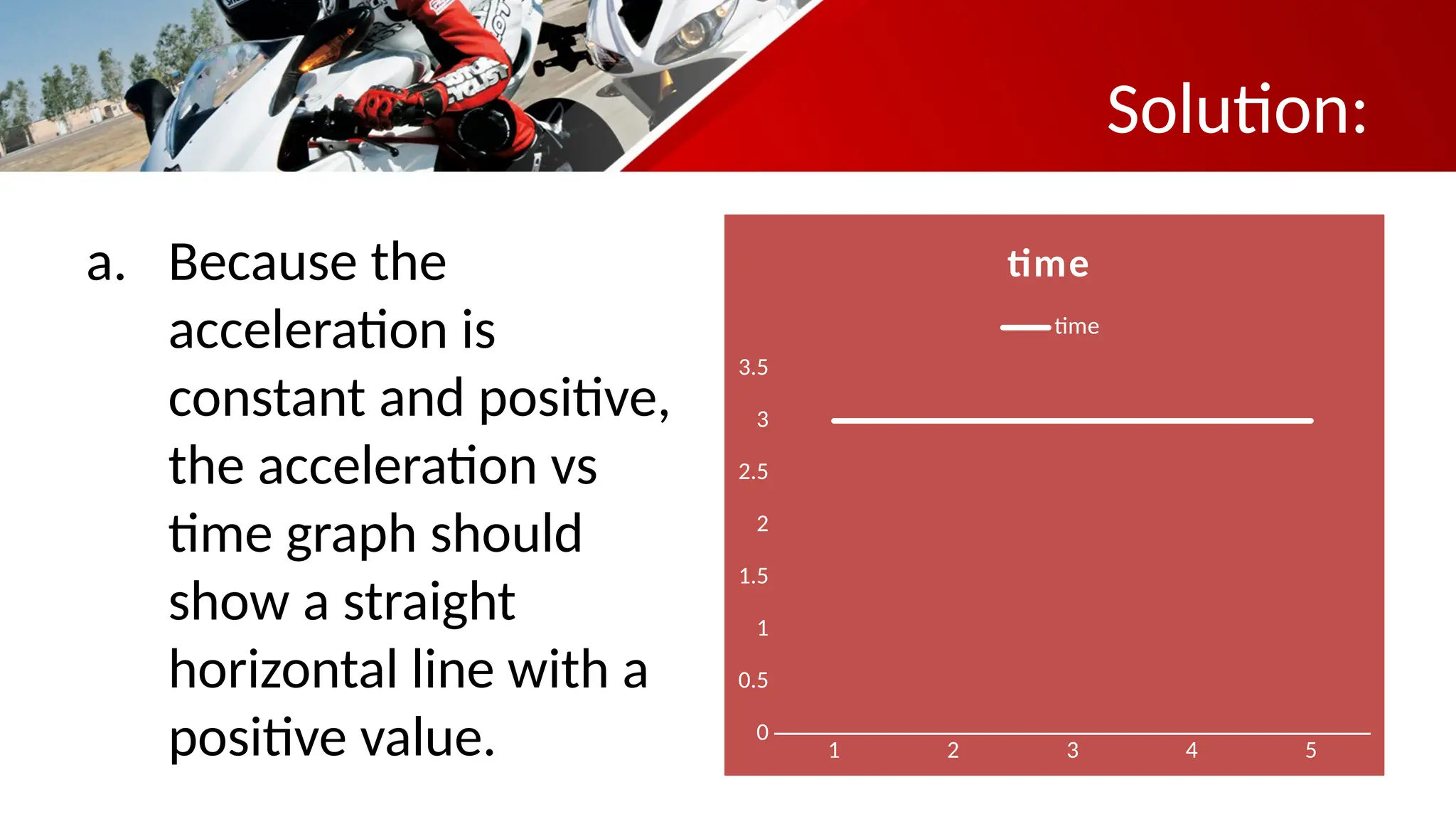
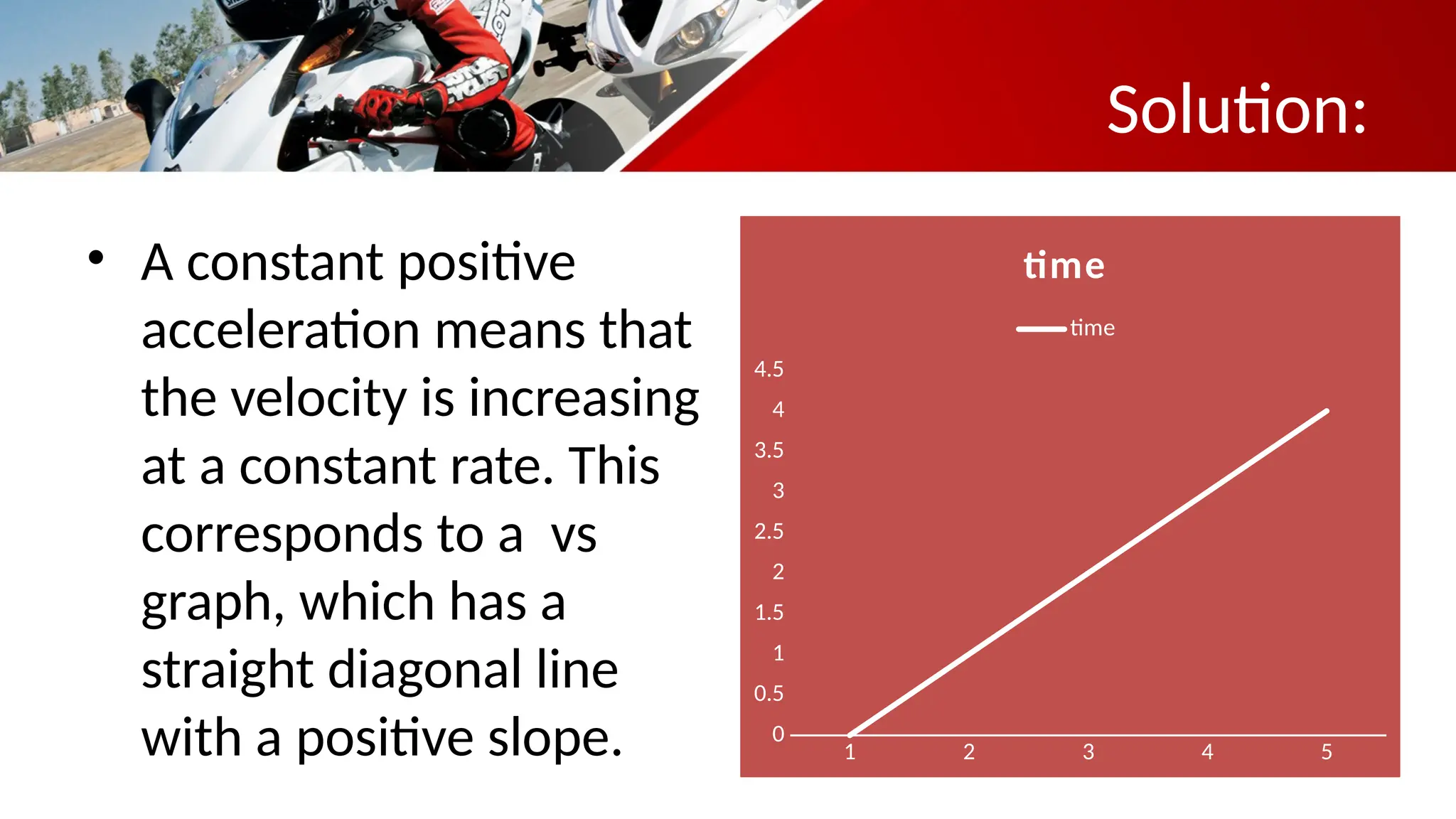
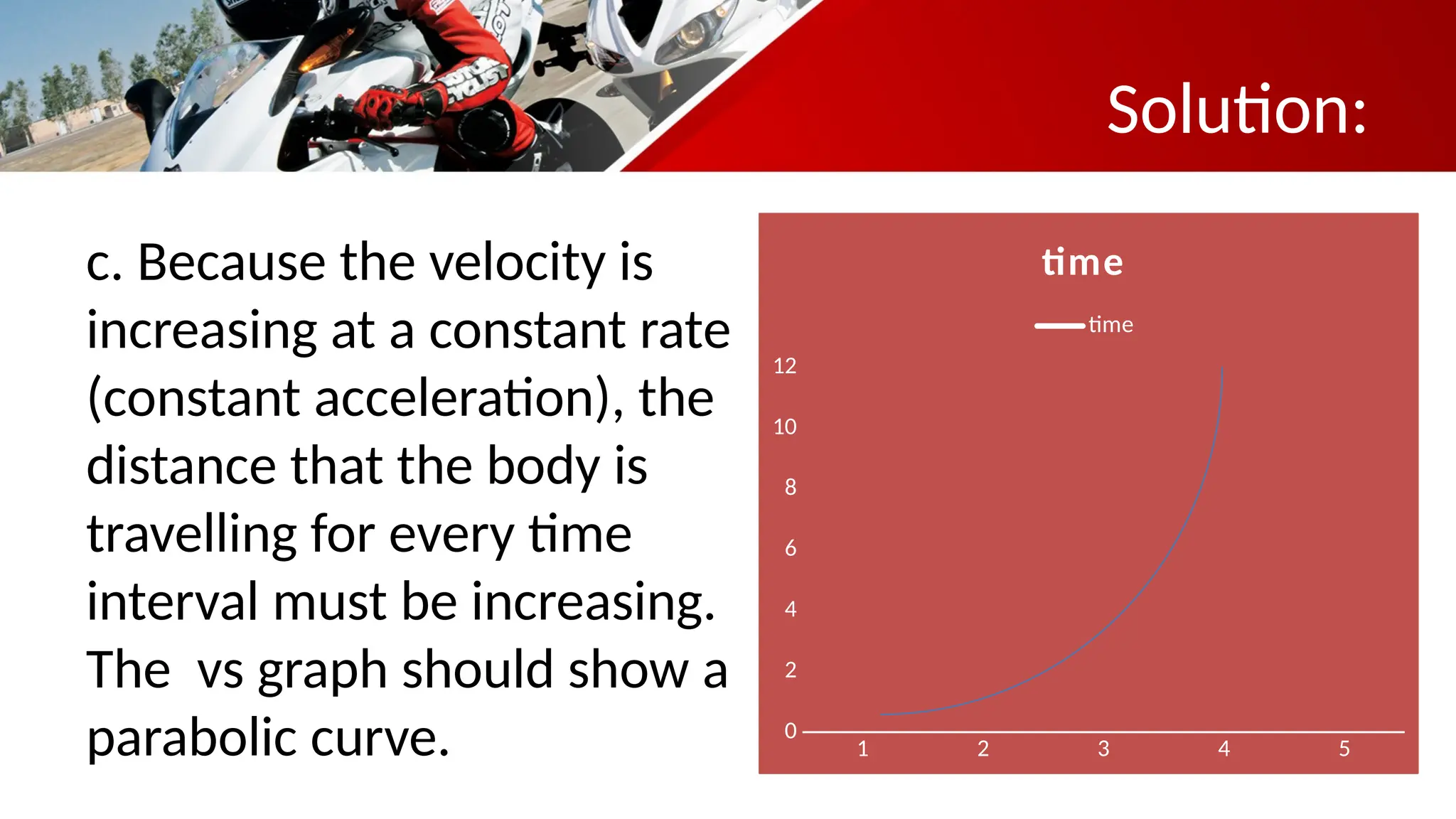
The document contains a mathematics prayer followed by quiz questions and exercises related to physics concepts like vector quantities, kinematics, and dynamics. It discusses various topics such as distance, displacement, speed, velocity, and acceleration, along with examples and problem-solving approaches. Additionally, it emphasizes the importance of graphs in understanding motion, showcasing how position, velocity, and acceleration can be represented graphically.

1. Mathematics Prayer
Dear God,
May we, through your blessings,
add purity to the world,
subtract evil from our lives,
multiply Your good news,
and divide Your gifts and share them with others.
Amen.

2. QUIZ # 2 (PINK PAPER)
What Have I Learned So Far?
Pages 20, 24, 28, and 31
Reflect Upon
Pages 20, 23, and 28

3. I. Write S if it is a scalar quantity,
or V if it is a vector quantity on
the space provided.
1. Amount of
substance
2. Torque
3. Speed
4. Potential
energy
5. Acceleration
6. Work done
7. Wavelength
8. Electric Field
9. Luminosity
10. Displacement

4. II. Solve for the resultant of the
following sets of vectors using the
specified method for each set.
1. Parallelogram method
Vector: A: 10m, 25
Vector: B: 6m, 15
2. Polygon method
Vector A: 10N, -35
Vector B: 5N, 45
Vector C: 1N, 85
3. Parallelogram and
polygon method
Vector: A: 7m/s, 0
Vector: B: 6m/s, 30
Vector C: 4m/s, 135

5. III. Find the resultants of the following
vectors using the analytical method.
1. Parallelogram method
Vector: A: 10m, 25
Vector: B: 6m, 15
2. Polygon method
Vector A: 10N, -35
Vector B: 5N, 45
Vector C: 1N, 85
3. Parallelogram and
polygon method
Vector: A: 7m/s, 0
Vector: B: 6m/s, 30
Vector C: 4m/s, 135

6. IV. Express the following vectors in
component form using unit vectors.
0

7. V. Express the following vectors in
component form, and then find
their magnitudes.

8. VI. Essay
1. Parallel lines are said to have the
same slope or inclination. Think of a
person who you think is “parallel” to
you – somebody who shares your
interests and who has the same
inclination as you. What are your
common interests?

9. VI. Essay
2. Which among the steps in the
analytical method did you find most
difficult? How were you able to
overcome this difficulty?

10. KINEMATICS
(QUANTITIES)
Module 3

11. Learning Competencies
• Interpret velocity and acceleration as slopes of
position vs time and velocity vs time curves
respectively.
• Construct velocity vs time and acceleration vs time
graphs corresponding to a given position vs time
graph and velocity vs time graph respectively.

12. Learning Competencies
• Distinguish distance from displacement, and speed
from velocity.
• Compute the speed, velocity, and acceleration of
moving bodies.
• Interpret displacement and velocity as areas under
velocity vs time and acceleration vs time curves,
respectively.

23. Organisms have different
ways to survive the wild.
• The survival in an ecosystem is a constant struggle
because of the scarcity of food and space.
• Predators must be fast enough to catch their prey.
• The prey must also have the means to avoid being
attacked and eaten.

24. Dragonflies can fly a distance
of about 29 km in one hour
to escape from predators.

25. Swan and geese can cruise at 64
km/h for many straight hours.

26. Cheetahs run at an average speed
of 110 km/h to catch their prey.

27. Peregrine falcons can briefly accelerate
to an enormous speed of 145 km/h
when they swoop down on their prey.

28. ETYMOLOGY
The word motion, which was first used in the
fourteenth century, came from the Latin word motio,
which means “movement”, from movére to move.

29. START UP (KDRAMA)

30. MECHANICS
• Describing motion is the focus of a field of physics.
• It is the study of motion.
• It is divided into two general parts (fields).
- KINEMATICS & DYNAMICS

31. KINEMATICS
It is a branch of physics and a subdivision of classical
mechanics concerned with the geometrically possible
motion of a body or system of bodies without
consideration of the forces involved (i.e., causes and
effects of the motions).
- britannica

32. KINEMATICS
• Is the mathematical description of motion.
• You can describe motion using kinematic quantities
such as position, speed, and acceleration.

33. DYNAMICS
• It is the study of the causes of motion.
For example, when an objects falls, you can say that
gravity is the cause of falling motion.

34. POSITION
• It is the fundamental concept in describing the
motion of object.
• It is the location of a body space with reference to a
fixed point.

36. DISTANCE
• It is the length of the path the body has taken.
• It is expressed in terms of magnitude and unit only.
• The SI unit for distance is meter.

37. Initial Position
• It is the position of the moving object that is usually
set to 0 m to serve as the reference point.
For example, if you walk a distance of 30 m in a straight
path from your house to your school, (on the next slide)

38. you are 30 m away from
your initial position.
30 m

39. DISTANCE
• Is also defined as the total length of the path taken
by the body.
In the previous example, suppose you went to the
library and to the store through this path on the next
slide.

40. The total distance you have traveled
is 30 m + 10 m + 40 m = 80 m
30 m 10 m
40 m

41. DISPLACEMENT
• It is defined as the length of the straight line formed
between the initial position and the final position of
an object.
• It is usually expressed in terms of magnitude, unit,
and direction.
• An arrow is placed on top of a symbol for
displacement denote its vector nature.

42. Displacement can be expressed
in units for lengths such as
meter and foot.
30 m 10 m
40 m
𝒅

43. DISPLACEMENT
• is defined to be the change in position of an object.
• it can be defined mathematically with the following
equation:
Displacement = Δ x = x f − x 0

44. Sample 3.1
Starting from the church, a procession has to take the
following route: 51m, north ; 42m, east; and 63 m
north. To go back, it has to follow the same route but in
the opposite direction.
a. What is the total distance traveled?
b. What is the total displacement?

45. Solutions:
a. Total distance traveled = 51m + 42m + 63m + 63m +
42m + 51m = 312m
b. The displacement is zero because the procession
went back to where it started.
Displacement Δ x = x f − x 0
Δ x = (156m - 156m)
Δ x = 0

46. SPEED AND VELOCITY
• Describing how fast or slow a body moves is
important.
For example, you can describe a moving car by its
speed.

48. In symbols,
• Get the ratio of the distance traveled by the body and
time it takes for the body to travel.
• Where d denotes the distance traveled for a time
interval t.
• Common units used for speed are m/s, km/s, & ft/s.

49. SPEED
• It is a scalar quantity because it is expressed only by
its magnitude and unit.
• The speed is fast if a long distance was covered for a
short time.
• The speed is slow when the period distance was
traveled for a long time.

50. Whenever you ride a car or a jeepney,
you probably notice that its speed
changes from time to time

51. INSTANTANEOUS SPEED
shows vehicle’s speed at a particular moment

52. ODOMETER
shows total distance travel by a vehicle

53. AVERAGE SPEED
Ratio of the total distance covered & the
total amount of time traveled

54. Example 1:
In the 1980’s, one of Asia’s fastest
running women was a Filipino
athlete named Lydia de Vega.
In the 100-meter dash event in
1986 in Seoul, south Korea, she
was clocked 11.53 s.
Find her average speed.

55. Solution:
Though the speed of a moving
objects tells you how fast it
moves, it does not give any
information on what direction
the object is moving.

58. VELOCITY
• It is the quantity that contains both the speed and
the direction of motion of a body.
• Unlike speed, it is a vector quantity.

59. SPEED & VELOCITY
• For example, if you say that a jeepney is travelling at 70
km/h, you are stating its speed.
But if you say that it moves at 70 km/h to the north,
you are now specifying the jeepney’s velocity.
• In everyday language, speed and velocity are used
interchangeably.
However, if the direction is significant in a situation, you
have to make distinction between these two.

60. UNIFORM CIRCULAR
MOTION
• Its speed is constant but its velocity is changing.
For example,
when an object is moving in a circle with constant speed,
the direction of its motion is always changing
(tangent to the circular path).

61. ACELERATION
• It is a measure of how fast or slow velocity changes.
• A body accelerates whenever there is a change in
speed, a change in direction of motion of the body,
or a change in both speed and direction.
• It can be easily computed as:

63. AVERAGE ACCELERATION
• If the acceleration is not constant.
• The instantaneous acceleration changes.
• Note that the change in velocity is the difference
between the final velocity.

64. 𝑎=
∆ 𝑣
∆ 𝑡
=
𝑣𝑓 −𝑣0
∆ 𝑡
The SI unit for acceleration must be

67. Sample Problem 3.2
Vania walks to her school away at a constant
speed of . Ten seconds later, her brother
Angelito follows at a constant speed of .
a. How long will it take Angelito to overtake
Vania?
b. How far is Vania from school when
overtaken by Angelito.

68. Solution:
Let t be the time for Angelito to overtake Vania.
Therefore, time Vania has been walking,
distance traveled by Angelito in time ,
distance traveled by Vania in time

69. a. To be overtaken, must be equal to .
Therefore,
Solving for .
b. First, we solve for the distance traveled by Vania
when Angelito had overtaken her.
Manipulating the equation and letting be the speed of
Vania,
Solution:

70. The school is away from Vania’s place. Therefore, Vania
is away from school when overtaken by Angelito.
Solution:

71. INCREASE OR DECREASE
POSITIVE ACCELERATION
When a body speeds up,
its final velocity is greater
than its initial velocity.
NEGATIVE ACCELERATION
When a body slows down.

72. • When a body has constant velocity, its acceleration is
equal to zero because the change in its velocity is
zero.
• There are cases wherein the magnitude of the
velocity (speed) is constant while its direction is
changing.
• The acceleration of the body moving is not zero.
UNIFORM
CIRCULAR MOTION

73. Example 2:
Consider the previous example. Suppose Lydia de Vega attained a
speed of after from the start of the race. Solve the following
problems using the given information:
a. What is her average acceleration during this time interval?
b. Suppose she attained a speed of after from the start of the race.
What is her average acceleration during the second time
interval?
c. Suppose at from the start of the race, she slows down to a speed
of for . What is her average acceleration for this time interval?

74. Solution:
a. As she is at rest at the
start of the race,
the initial speed is

75. Solution:
b. The acceleration for the
time interval between 2 s
and 8 s from the start of the
race.
the initial speed and final
speed should be and ,
respectively.

76. Solution:
c. For this time interval, the
initial speed and the final
speed are and ,
respectively.
As the elapsed time is
Take note that acceleration
is negative she has slowed
down.

77. Sample Problem 3.3
A lady passenger steps on one end of a moving
sidewalk in an airport terminal like the one shown in
the figure. The sidewalk is long and is moving at . Find
the time taken by the lady to reach the other end of the
sidewalk

78. Solution:
a. The time taken by the lady passenger to reach the
other end of the sidewalk is equal to m divided by ,
that is, .
b. The time taken by the lady passenger to reach the
other end of the sidewalk is equal to divided by
that is,

79. Sample Problem 3.4
The position of an object as a function of time t is given
by
a. Give the velocity and acceleration as a function of
time.
b. Find the velocity and acceleration at

80. Solution:
a.1.

81. Solution:
a.2.

82. b. Substituting t = 2.0 s to (1) and (2),
2

83. GRAPHICAL
DESCRIPTION OF MOTION
• The motion of a body can easily be described using
graphs.
• Example is graph position versus time.
• If you set the initial position of the object to zero, you
have a distance traveled vs time (d vs t) graph.

84. • Imagine a jeepney moving at a constant velocity of to
the right.
• Its position increases by every second.
• Thus, the position of the jeepney increases linearly in
time.
GRAPHICAL
DESCRIPTION OF MOTION

85. A jeepney moving at a
constant velocity of 30 m/s.
0 m 30 m 60 m 90 m 120 m 150 m
𝑡=0 𝑠 𝑡=1𝑠 𝑡=2𝑠 𝑡=3 𝑠𝑡=4 𝑠𝑡=5 𝑠

86. Graph of position vs time for
jeepney moving at constant
velocity of 30 m/s.
1.0 2.0 3.0 4.0 5.0
0
20
40
60
80
100
120
140
160
30
60
90
120
150
time, t (s)
∆𝑡=1.0 𝑠
(𝑟𝑢𝑛)
∆𝑑=30 𝑚
(𝑟𝑖𝑠𝑒)

87. Recall how the slope of
the line is obtained.
• Slope is defined as the ratio of the “rise” and the
“run,” that is, the ratio of the changes of the changes
in the values plotted in the - and -axes. In a vs graph,
the change in the -axis corresponds to the time
interval
• Therefore,

88. Based on the definition of the
average speed,
• The slope of the line in a vs graph is equal to the
magnitude of the velocity (speed).
• If the graph is a curve rather than straight line, the slope
at any point is defined as the slope of the line tangent to
the curve at that point.
• Note that a curve has an infinite number of points.
• This means that the slope of the tangent line
corresponds to the instantaneous speed.

89. In the graph, given that the slopes of
the tangent lines increase as time
increases, the instantaneous speed
increases as well.
1.0 2.0 3.0 4.0 5.0
0
20
40
60
80
100
120
140
160
30
60
90
120
150
time, t (s)
∆𝑥
∆𝑦
∆𝑥
∆𝑦

90. Velocity vs time graph
• Take the same jeepney moving at a constant velocity
of to the right.
• In this case, the dependent variable is the velocity,
and the independent variable is the time.
• With a constant velocity, the velocity versus time
graph is a straight horizontal line as shown on the
next slide.

91. Graph of velocity vs time for a
body with constant velocity
1.0
2.0
3.0
4.0
5.0
0 10 20 30 40 50 60
50
50
50
time t(s)
time t(s)

92. Note that the shaded
region is rectangular.
• Thus, the area is simply the product of the shape’s
length and width.
• The length corresponds to the time interval , and the
width to velocity

93. Note that the area under the curve of the vs
graph corresponds to which is the distance
traveled in a particular time interval.
To summarize the important relations so far:
• In a position versus time graph the slope of the line is
equal to the speed (magnitude of velocity).
• In a velocity versus time graph, the area under the curve
corresponds to the distance traveled at a particular time
interval.
• Also, the slope of the line in the vs graph is the
acceleration of the object.

94. Example 3:
Consider a body moving with constant positive
acceleration.
a. Construct an arbitrary acceleration vs time graph.
b. Supporting that the body started from rest,
construct an arbitrary velocity time graph.
c. Setting the initial position of the body to zero,
construct an arbitrary position vs time graph.

95. Solution:
a. Because the
acceleration is
constant and positive,
the acceleration vs
time graph should
show a straight
horizontal line with a
positive value. 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
time
time

96. Solution:
• A constant positive
acceleration means that
the velocity is increasing
at a constant rate. This
corresponds to a vs
graph, which has a
straight diagonal line
with a positive slope. 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
time
time

97. Solution:
c. Because the velocity is
increasing at a constant rate
(constant acceleration), the
distance that the body is
travelling for every time
interval must be increasing.
The vs graph should show a
parabolic curve. 1 2 3 4 5
0
2
4
6
8
10
12
time
time

98. POINTS TO PONDER
Each body has a motion that
can be described both
qualitatively (through verbal
description) and
quantitatively (through
mathematics).

99. POINTS TO PONDER
Displacement measures how far a
body has gone or traveled with respect
to its initial position.
If this will be applied in life,
displacement can be a measure of how
much one has changed, or how much
one has reached his or her goal.

100. POINTS TO PONDER
Graphing is a convenient way to
describe how a body moved.
Graphs are visual representations
of the equations that you work
on.

101. Submission Dates to
Remember:
January 22, 2024 -
PETA 1 (Beyond Walls pages 4-5)
January 29, 2024 -
PETA 2 (Beyond Walls page 14)
THIRD QUARTER CULMINATING OUTPUT
(pages 129-130)
Submission date is on or before February 16, 2024.

102. Submission Dates to
Remember:
February 5, 2024 -
PETA 3 (Beyond Walls page 21)
February 12, 2024 -
PETA 4 (Beyond Walls page 29)

103. Submission Dates to Remember:
February 19, 2024 -
PETA 5 (Beyond the Walls page 39)
February 26, 2024 -
PETA 6 (Beyond the Walls page 44)

104. PETA 5
• One of the goals of the government
is to maximize road accidents due to
over speeding along highways.
• The mayor in your city hired a
documentary director to create an
infomercial about over speeding.

105. PETA 5
• As an active member of traffic
enforcers in town, you have been
asked to discuss and share the
dangers of overs peeding along
highways and other major
thoroughfares based on your own
experiences and observations.

106. PETA 5
• Your answers will be assessed by the
director based on the accuracy of
the concepts of speed and
acceleration that you used in it, your
efficient retelling and sharing of
your experience as an enforcer to
make the discussion realistic, and
how interactive your presentation is.

107. PETA 6
• Jonda, a car manufacturer, has just
expanded its sales thrust and started
selling online brand new cars to its
potential clients.
• You have been tasked by your manager
to explain to a potential client how the
latest car model of Jonda efficiently
uses fuel whenever it accelerates.

108. PETA 6
• Make a draft of your explanation
before presenting it to the client.
• Present your work first to your
manager for evaluation and
approval.

109. PETA 6
• He will check and validate your draft
based on the correctness and
consistency of your explanation about
the concept of acceleration and how the
car model operates, your strategic use of
appropriate words in your sales talk, and
your ability to empathize with the
potential customer during the discussion.

110. HW#1 DREAM FIELDTRIP
Plan your dream travel itineraries. I will be assigning
reference point for the whole class. You can use google
maps (http://maps.google.com)
You will gather data of distance between one place and
another.
You will compute the total distance travel and total
displacement.

111. CHIT CHAT TIME
(Q & A)