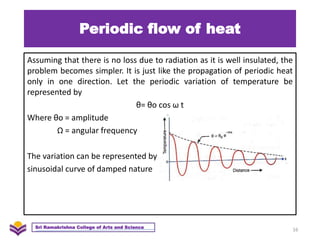
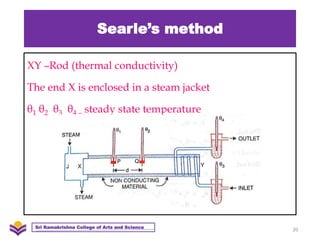
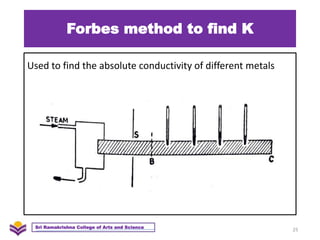
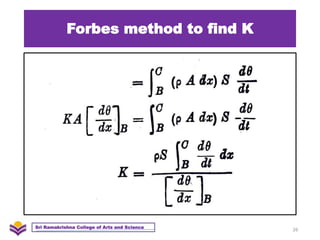
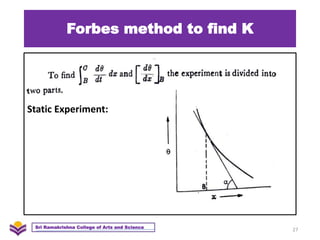
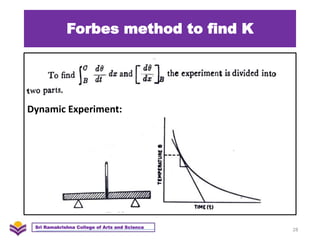
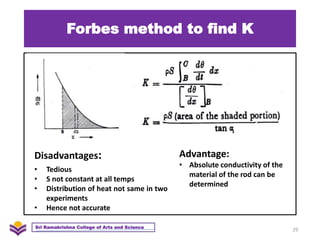
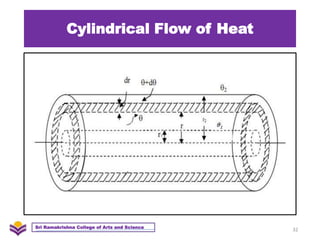
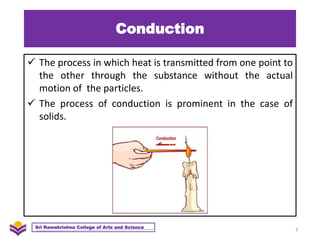
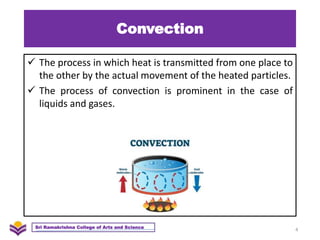
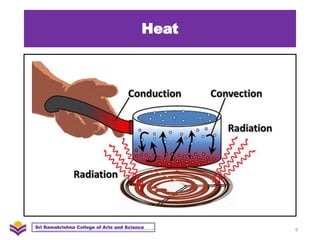
The document discusses heat transfer and thermal conductivity. It defines heat transfer as the process by which internal energy transfers from one substance to another. The three main modes of heat transfer are conduction, convection, and radiation. Conduction involves heat transfer through direct contact without particle movement. Convection occurs through the movement of heated particles. Radiation transfers heat directly through space without an intervening medium. Thermal conductivity is measured as the rate of heat transfer and can be used to analyze heat flow in materials.





![Coefficient of thermal
conductivity
Dimensions of K
K = -Q/A
𝑑𝜃
𝑑𝑥
𝑡
[Q] = [ML2T-2 ], [dx] = [L], [A] = [L2], [dθ] = [θ], [t]= [T]
Therefore
[K] = [MLT-3θ-1]
9
Sri Ramakrishna College of Arts and Science](https://image.slidesharecdn.com/u2-ppt-240416034721-a90eecef/85/Physics-Heat-and-Thermodynamics-Basics-9-320.jpg)