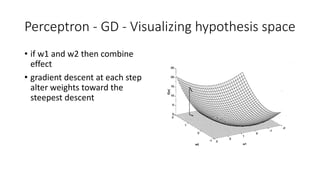
Perceptrons are a type of artificial neural network where each unit is called a perceptron. Perceptrons take a vector of inputs and can only deal with linearly separable functions like AND and OR, but not XOR. The perceptron training rule modifies weights at each step according to the error between the target and actual output. If there is no error, the weights are not updated. Gradient descent was introduced to handle non-linearly separable functions by finding weights for the best fit without a threshold, by minimizing the squared error over all training examples through iterative weight updates in the direction of steepest descent. The delta rule for gradient descent is similar to the perceptron rule but uses the linear unit output rather than the

1. PERCEPTRONS
Umair Ali

2. Perceptron - introduction
• ANN based on unit is called
perceptron
• Perceptrons takes the vector of
inputs
• can deal linear separable
functions only like AND or but
not XOR

3. Perceptron - Representations
• let make an example
• mainly two rules are under consideration
• weights are modified at each step
according to Perceptron taining rule
• delW is updated error while wi is previous
error
• if t-o = 0 then no need to update weights
• if t-o = a then w+a will be new weight
• this hold for only linear separable
function

4. coding for perceptron training rule
• import numpy as np
• inputs = np.array([[0,0,-1],[0,1,-
1],[1,0,-1],[1,1,-1]])
• targets = np.array([[1],[0],[0],[0]])
• weights = np.array([[0.2],[0.1],[0.2]])
• for n in range(4):
•
• out = np.dot(inputs,weights)
• out=np.where(out>0,1,0)
•
• weights -=
0.25*np.dot(np.transpose(inputs
),(out-targets))
•
• print ("Iteration: ", n)
• print (weights)
• print (out)

5. Perceptron - Gradient Descent or delta rule
• perceptron rule is not for linearly
separable
• due to this deficiency delta rule
is introduced for best fitting
• main purpose is to find weights
for best fitting targets
• WITHOUT any threshold
• (t-o)^2 summed over all training
examples.
• D is training example(d) set and

6. Perceptron - GD - Visualizing hypothesis space
• if w1 and w2 then combine
effect
• gradient descent at each step
alter weights toward the
steepest descent

7. Perceptron - GD - Derivation of GD rule
• steepest descent can achieve each
by taking dervative of error wrt to
current weight
• Training rule for gradient descent is
• - sign indicate we want to move w
vector in direction of decreasing
error
• for practical implementation we
need gradient at each step
•

8. perceptron -GD - derivation
• xid is single input for training
example d
• training example (x,t) input,
target
• Notice
• the delta rule in Equation (4.10) is similar to
the perceptron training rule in
• Equation (4.4.2). In fact, the two expressions
appear to be identical. However,
• the rules are different because in the delta
rule o refers to the linear unit output
• o(2) = i;) .?, whereas for the perceptron rule o
refers to the thresholded output
• o(2) = sgn($ .2)