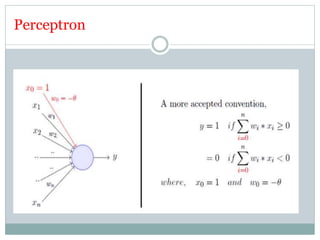
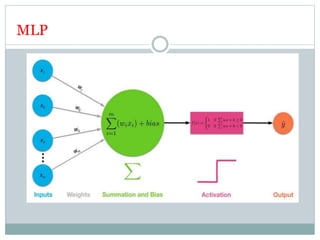
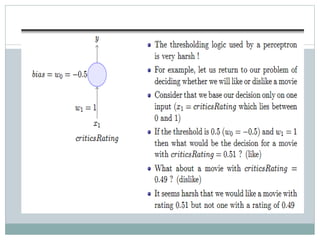
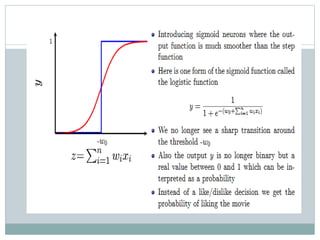
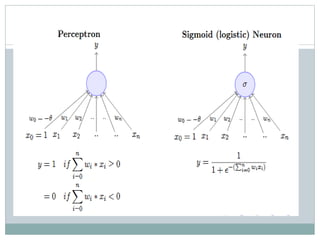
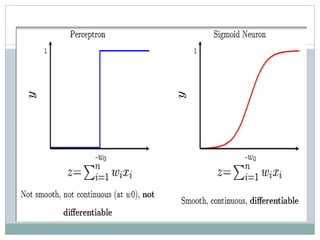
This document discusses perceptron and sigmoid neurons. It defines perceptrons as computational models that take real-valued inputs, aggregate them using weighted sums, and output binary values based on a threshold. Perceptrons are linear classifiers. Sigmoid neurons are then introduced to address limitations of perceptrons by having real-valued inputs and outputs between 0-1. Multi-layer perceptrons are described as neural networks with multiple hidden layers that use backpropagation to train the network weights to minimize error between predicted and actual outputs.

1. Perceptron &
Sigmoid Neurons
Dr.S.SHAJUN NISHA, MCA.,M.Phil.,M.Tech.,MBA.,Ph.D
Assistant Professor & Head
PG & Research Dept. of Computer Science
Sadakathullah Appa College
shajunnisha_s@yahoo.com
+91 99420 96220

2. Perceptron
 Frank Rosenblatt, an American psychologist,
proposed the classical perceptron model(1958)
 A more general computational model than
McCulloch–Pitts neurons
 Main differences: Introduction of numerical
weights for inputs and a mechanism for learning
these weights
 Input-Real Value
 Output- Binary (0,1)

3. Perceptron
 It takes an input, aggregates it (weighted sum) and
returns 1 only if the aggregated sum is more than
some threshold else returns 0
 Perceptron is usually used to classify the data into
two parts. Therefore, it is also known as a Linear
Binary Classifier.

4. Perceptron

5. Bias
 In the above diagram, x0 is bias input.
 Bias is an additional parameter in the Neural
Network which is used to adjust the output along
with the weighted sum of the inputs to the neuron.
 Therefore Bias is a constant which helps the model in
a way that it can fit best for the given data.
 bias helps in controlling the value at which activation
function will trigger

6. OR with Perceptron

7. Learning Algorithm

8. Multi Layer Perceptron (MLP)
 Multi-layer Perceptron model (MLP) is an artificial
neural network with three or more hidden layers.
 It is a feed-forward neural network that uses back
propagation technique for training the network.
 Multi-layer perceptron model is sometimes
referred to as the deep neural network because it
has many hidden layers.

9. MLP
 It is a deep learning method used for supervised
learning and its capable of modeling complex
problems.
 Multi-layer perceptron is capable of handling both
linearly and non-linearly separable tasks.

10. MLP

11. MLP
 There are 2 stages in learning process
 Feedforward
 Backpropagation

12. Feed Forward
 The input layer receives the features from the data
set each node representing a feature
 bias is added to the sum of input and weight
 The information from the input layer is sent to each
neuron in the hidden layer for further processing

13.  The neurons in the hidden layer accepts the
information from input layer together with their
weights and biases.
 The neuron has an activation function which
regulates the processing of information in the
neuron
 The activation function ensures that the information
is within the required range such as 0 to 1 or -1 to 1

14.  The output from one layer is the input in the next
layer.
 When the information moves from one layer to the
next layer it is multiplied by the weights and bias
added.
 The final hidden layer is the output layer and is
responsible for predicting the results of the model

15. Back Propagation
 We can improve the accuracy of the prediction
by adjusting weights and biases in a backward
direction.
 The objective of back propagation is to reduce the
error
 Error(loss function)=Expected Output-Actual
Output
 There are many types of loss functions such as
Root Mean Squared Error (RMES)
Cross Entropy (CE)

16.  The error is reduced through what is called the
gradient descent process which uses the
derivatives to find the gradient/slope of the error
function
 The objective of gradient descent is to move the
error to the zero level

17. Sigmoid Neurons
 Why Sigmoid Neuron?
 MP-Neuron
Input and Output= Binary
 Perceptron
Input=Real value, Output=Binary
Can’t handle linearly non-separable problems
 MLP(Network of Perceptron)
Input=Real value, Output=Binary
Can handle linearly non-separable problems

18. Sigmoid Neuron
 Both input and Output are real values
 Output of sigmoid neuron is a real value between 0
and 1, which is smoother than binary input
 There are many functions with the characteristic of
an “S” shaped curve known as sigmoid functions
 The most commonly used function is the logistic
function

25. Learning Algorithm
 The objective of the learning algorithm is to
determine the best possible values for the
parameters (w and b), such that the overall loss
(squared error loss) of the model is minimized as
much as possible.

26. Algorithm