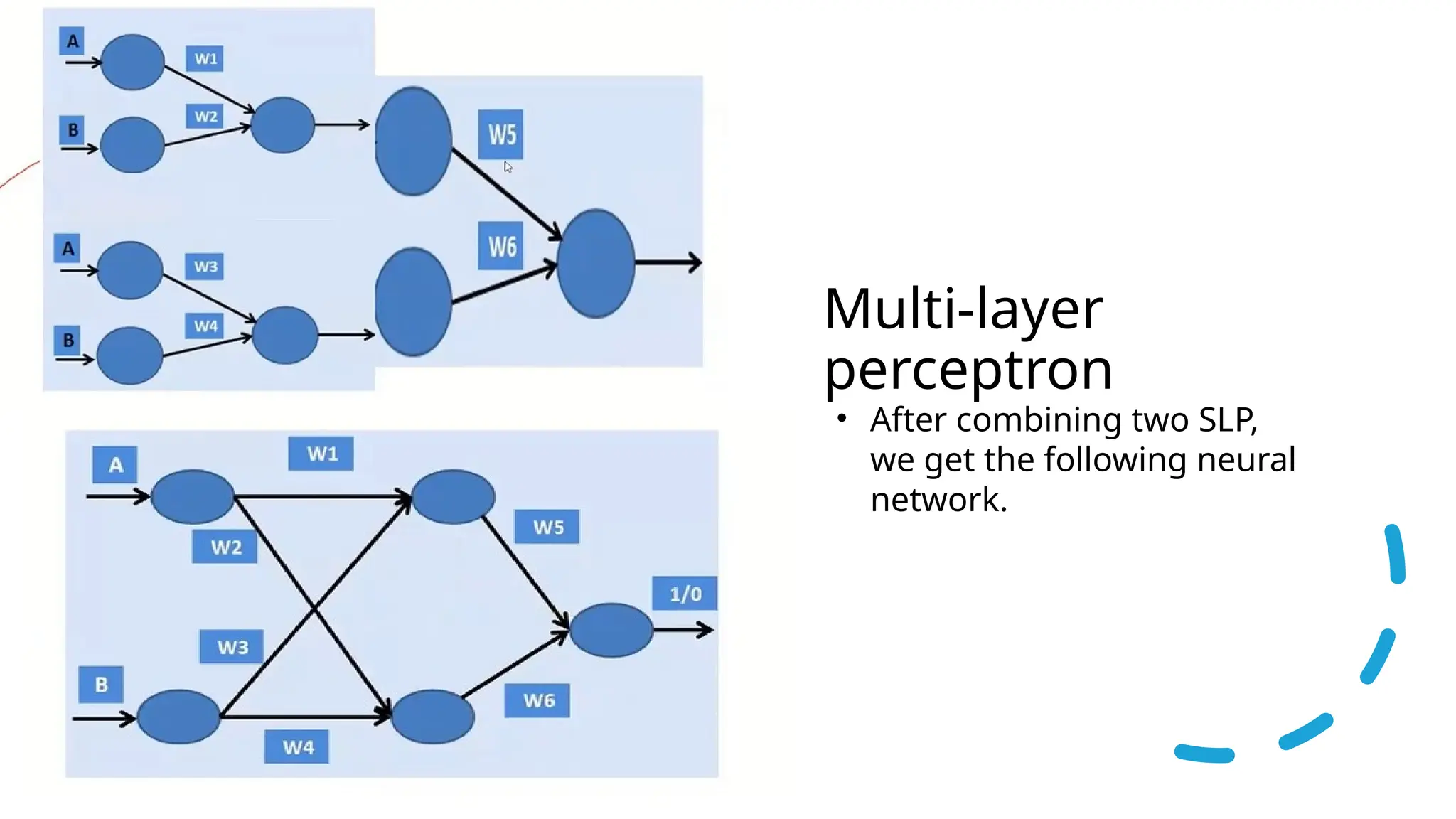
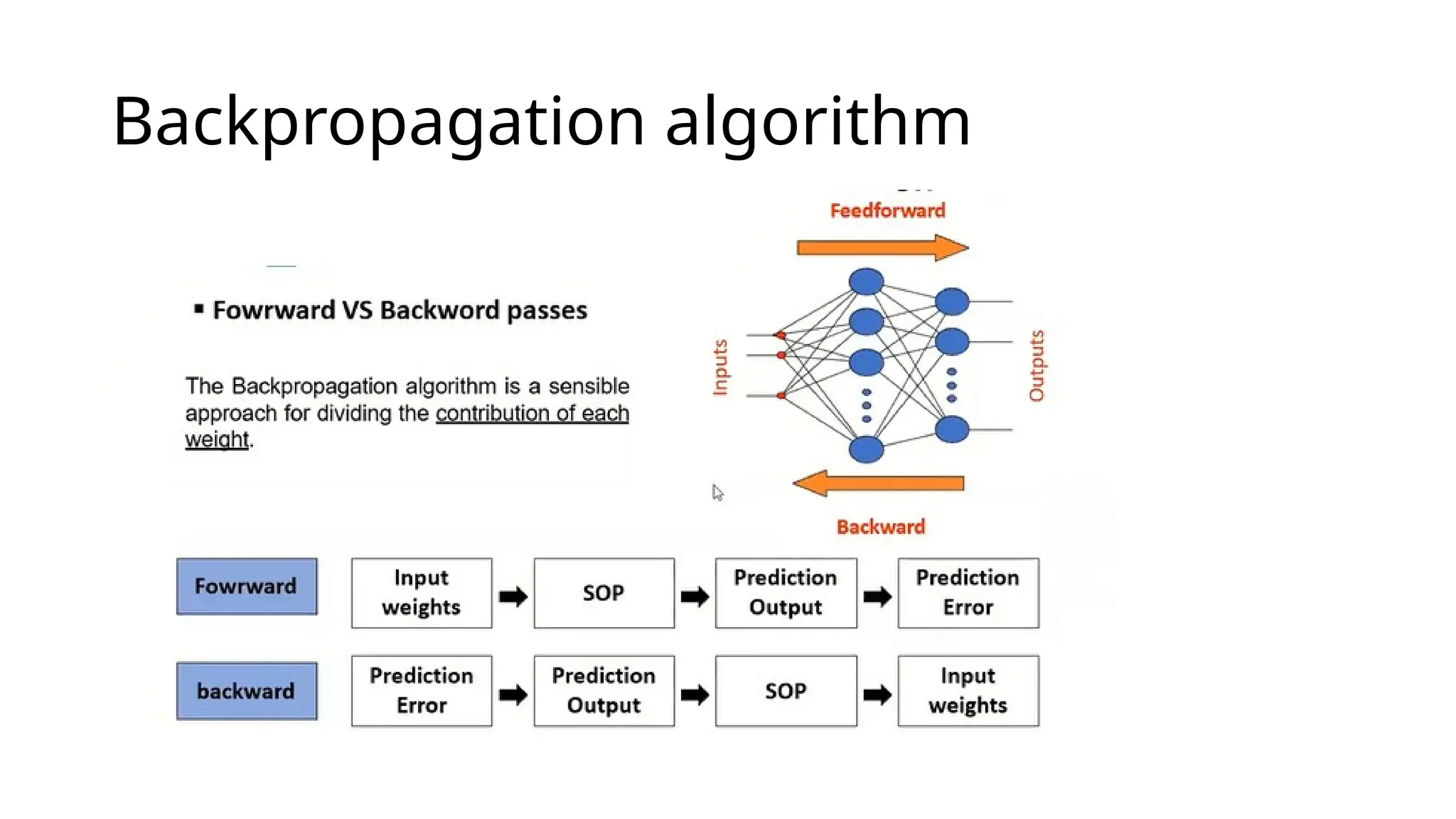
This document discusses multi-layer perceptrons (MLPs), which are types of artificial neural networks capable of learning complex, non-linear patterns in data through layers of neurons and using non-linear activation functions. It explains the processes involved in training MLPs, specifically focusing on the backpropagation algorithm, which optimizes the network by adjusting weights and biases to minimize a loss function. The document further elaborates on gradient descent methods for finding optimal model parameters and outlines steps for applying the backpropagation algorithm.

1. Backpropagation Neural networks (Multi-
layer perceptron)
Artificial Intelligence _ Lab 6

2. Multi-layer
perceptron
• Unlike single layer
perceptron, multi-layer
perceptron uses non-linear
dat​
a or non-linearly
separable.
• For example, we have non-
linear data. Thus, we have
to separate our samples
using two or more lines.
This depicts MLP.

3. Multi-layer
perceptron

4. Multi-layer
perceptron
• After combining two SLP,
we get the following neural
network.

5. Backpropagation Algorithm
• A multi-layer perceptron (MLP) is a type of artificial neural network consisting of
multiple layers of neurons. The neurons in the MLP typically use nonlinear
activation functions, allowing the network to learn complex patterns in data. MLPs
are significant in machine learning because they can learn nonlinear relationships
in data, making them powerful models for tasks such as classification, regression,
and pattern recognition.
• Neural networks are trained using techniques called feedforward propagation
and backpropagation.
• During feedforward propagation, input data is passed through the network layer
by layer, with each layer performing a computation based on the inputs it receives
and passing the result to the next layer. Feedforward neural networks (FNN) are
the simplest form of ANNs, where information flows in one direction, from input to
output. There are no cycles or loops in the network architecture. Multilayer

6. Backpropagation Algorithm
• Backpropagation is an algorithm used to train neural networks by iteratively adjusting the network's weights and biases in order to minimize the loss
function. A loss function (also known as a cost function or objective function) is a measure of how well the model's predictions match the true target
values in the training data. The loss function quantifies the difference between the predicted output of the model and the actual output, providing a
signal that guides the optimization process during training. In RNNs (Recurrent Neural Network), connections between nodes form directed cycles,
allowing information to persist over time. This makes them suitable for tasks involving sequential data, such as time series prediction, natural
language processing, and speech recognition.
• In machine learning, backpropagation is an effective algorithm used to train artificial neural networks, especially in feed-forward neural networks. In
each epoch, the model adapts these parameters, reducing loss by following the error gradient.
• The goal of training a neural network is to minimize this loss function by adjusting the weights and biases. These adjustments are guided by an
optimization algorithm, such as gradient descent or stochastic gradient descent.
• Stochastic Gradient Descent (SGD) Gradient Descent is an iterative optimization process that searches for an objective function’s optimum value
(Minimum/Maximum). It is one of the most used methods for changing a model’s parameters in order to reduce a cost function in machine learning
projects.
• The primary goal of gradient descent is to identify the model parameters that provide the maximum accuracy on both training and test datasets. In
gradient descent, the gradient is a vector pointing in the general direction of the function’s steepest rise at a particular point. The algorithm might
gradually drop towards lower values of the function by moving in the opposite direction of the gradient, until reaching the minimum of the function.
• To solve problem of MLP or find the best weights for multi-layer neural networks. We used backpropagation algorithm.

7. Backpropagation
algorithm

8. Backpropagation algorithm

9. Backpropagation algorithm Example
• To solve examples based on backpropagation, we follow the
following steps:-

10. Backpropagation algorithm Example
• Solve this example using BP algorithm using sigmoid
activation function, error or mean square error = 0.5
*(desired – predicted)^2
•
Activation function

11. Backpropagation algorithm Example

12. Backpropagation algorithm Example

13. Backpropagation algorithm Example

14. Backpropagation algorithm Example
And so on until we reach that
total error in one epoch <=
required error

15. Backpropagation algorithm Example