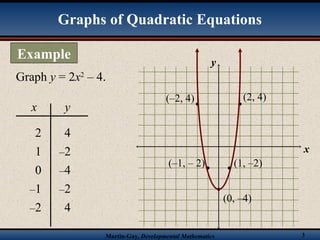
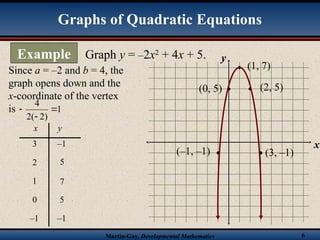
The document explains the process of graphing quadratic equations, focusing on key elements such as the vertex and axis of symmetry. It provides examples for finding x-intercepts and y-intercepts and discusses the characteristics of parabolas based on the coefficients of the standard form equation. The document emphasizes the significance of understanding these concepts in effectively graphing quadratic equations.

1. Graphing Quadratic
Equations in Two
Variables

2. Martin-Gay, Developmental Mathematics 2
We spent a lot of time graphing linear equations in
chapter 3.
The graph of a quadratic equation is a parabola.
The highest point or lowest point on the parabola
is the vertex.
Axis of symmetry is the line that runs through the
vertex and through the middle of the parabola.
Graphs of Quadratic Equations

3. Martin-Gay, Developmental Mathematics 3
x
y
Graph y = 2x2
– 4.
x y
0 –4
1 –2
–1 –2
2 4
–2 4
(2, 4)
(–2, 4)
(1, –2)
(–1, – 2)
(0, –4)
Graphs of Quadratic Equations
Example

4. Martin-Gay, Developmental Mathematics 4
Although we can simply plot points, it is helpful
to know some information about the parabola
we will be graphing prior to finding individual
points.
To find x-intercepts of the parabola, let y = 0
and solve for x.
To find y-intercepts of the parabola, let x = 0
and solve for y.
Intercepts of the Parabola

5. Martin-Gay, Developmental Mathematics 5
If the quadratic equation is written in standard
form, y = ax2
+ bx + c,
1) the parabola opens up when a > 0 and
opens down when a < 0.
2) the x-coordinate of the vertex is .
a
b
2

To find the corresponding y-coordinate, you
substitute the x-coordinate into the equation
and evaluate for y.
Characteristics of the Parabola

6. Martin-Gay, Developmental Mathematics 6
x
y
Graph y = –2x2
+ 4x + 5.
x y
1 7
2 5
0 5
3 –1
–1 –1
(3, –1)
(–1, –1)
(2, 5)
(0, 5)
(1, 7)
Since a = –2 and b = 4, the
graph opens down and the
x-coordinate of the vertex
is 1
)
2
(
2
4



Graphs of Quadratic Equations
Example