AK
Uploaded byAkila Krishnamoorthy
PPTX, PDF1,696 views

Slr parser

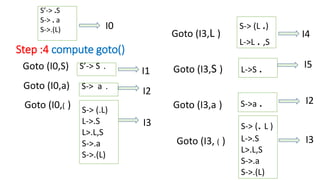
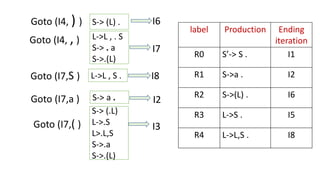
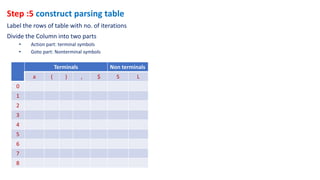
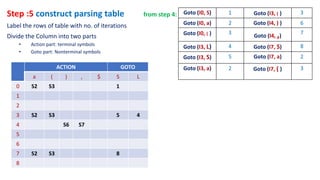
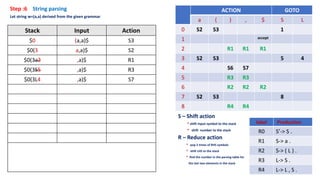
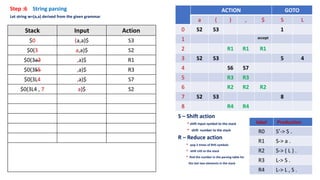
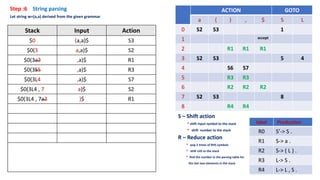
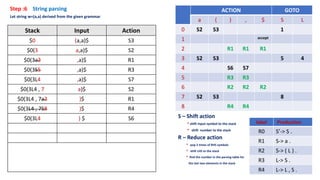
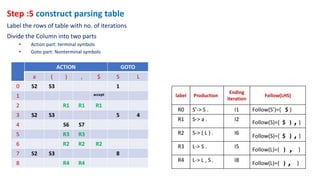
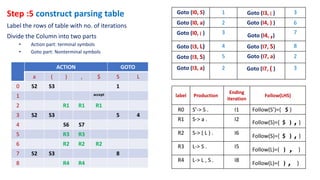
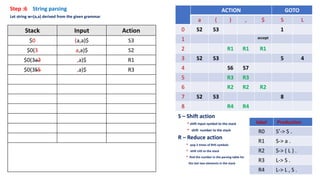
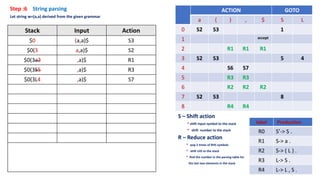
The document describes the steps of SLR parsing: 1. Create an augmented grammar by adding a new start symbol S' and the production S' -> S. 2. Generate kernel items by introducing dots in productions. 3. Find the closure of kernel items. 4. Compute the goto table from the closure sets. 5. Construct the parsing table from the goto table and closure sets. 6. Parse input strings using the parsing table and stack.

Embed presentation

Downloaded 10 times
SLR PARSER Steps: 1. create augment grammar 2. generate kernel items 3. find closure 4. compute goto() 5. construct parsing table 6. parse the string Let us consider grammar: S->a S->(L) L->S L->L,S
• Step :1 Create augment grammar S is start symbol in the given grammar Augment grammar is S’-> S • Step :2 Generate kernel items Introduce dot in RHS of the production`` S’-> .S • Step :3 Find closure (Rule: A -> α.Xβ i.e if there is nonterminal next to dot then Include X production)) S’-> .S S-> . a S->.(L) I0
Step :4 compute goto() S’-> S . I1 Goto (I0,a) S-> a . I2 Goto (I0,( ) S’-> .S S-> . a S->.(L) I0 S-> (.L) L->.S L>.L,S S->.a S->.(L) I3 Goto (I3,L ) S-> (L .) L->L . ,S I4 Goto (I3,S ) L->S . I5 Goto (I3,a ) S->a . I2 Goto (I3, ( ) S-> (. L ) L->.S L>.L,S S->.a S->.(L) I3 Goto (I0,S)
Goto (I4, ) ) S-> (L) . I6 Goto (I4, , ) L->L , . S S-> . a S->.(L) I7 Goto (I7,S ) L->L , S . I8 Goto (I7,a ) S-> a . I2 Goto (I7,( ) S-> (.L) L->.S L>.L,S S->.a S->.(L) I3 label Production Ending iteration R0 S’-> S . I1 R1 S->a . I2 R2 S->(L) . I6 R3 L->S . I5 R4 L->L,S . I8
Step :5 construct parsing table Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols Terminals Non terminals a ( ) , $ S L 0 1 2 3 4 5 6 7 8
Step :5 construct parsing table from step 4: Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 2 3 S2 S3 5 4 4 S6 S7 5 6 7 S2 S3 8 8 Goto (I0, S) 1 Goto (I3, ( ) 3 Goto (I0, a) 2 Goto (I4, ) ) 6 Goto (I0, ( ) 3 Goto (I4, ,) 7 Goto (I3, L) 4 Goto (I7, S) 8 Goto (I3, S) 5 Goto (I7, a) 2 Goto (I3, a) 2 Goto (I7, ( ) 3
Step :5 construct parsing table Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 label Production Ending iteration Follow(LHS) R0 S’-> S . I1 Follow(S’)={ $ } R1 S-> a . I2 Follow(S)={ $ ) , } R2 S-> ( L ) . I6 Follow(S)={ $ ) , } R3 L-> S . I5 Follow(L)={ ) , } R4 L-> L , S . I8 Follow(L)={ ) , }
Step :5 construct parsing table Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 label Production Ending iteration Follow(LHS) R0 S’-> S . I1 Follow(S’)={ $ } R1 S-> a . I2 Follow(S)={ $ ) , } R2 S-> ( L ) . I6 Follow(S)={ $ ) , } R3 L-> S . I5 Follow(L)={ ) , } R4 L-> L , S . I8 Follow(L)={ ) , } Goto (I0, S) 1 Goto (I3, ( ) 3 Goto (I0, a) 2 Goto (I4, ) ) 6 Goto (I0, ( ) 3 Goto (I4, ,) 7 Goto (I3, L) 4 Goto (I7, S) 8 Goto (I3, S) 5 Goto (I7, a) 2 Goto (I3, a) 2 Goto (I7, ( ) 3
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 $0(3L4 ) $ S6 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 $0(3L4 ) $ S6 $0(3L4)6 $ R2 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
Step :6 String parsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 $0(3L4 ) $ S6 $0(3L4)6 $ R2 $0S1 $ accept Hence the string parsed successfully !!!!!! label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .

More Related Content

PPTX
CLR AND LALR PARSER
byAkila Krishnamoorthy
 
PPTX
Compiler Design Unit 2
byJena Catherine Bel D
 
PPTX
Shift reduce parser
byTEJVEER SINGH
 
PPT
Top down parsing
byASHOK KUMAR REDDY
 
PPTX
LR(1) and SLR(1) parsing
byR Islam
 
PPT
Bottom - Up Parsing
bykunj desai
 
PPTX
Compiler design syntax analysis
byRicha Sharma
 
PDF
Bottom up parser
byEsmeraldaAkshu1
 
CLR AND LALR PARSER
byAkila Krishnamoorthy
 
Compiler Design Unit 2
byJena Catherine Bel D
 
Shift reduce parser
byTEJVEER SINGH
 
Top down parsing
byASHOK KUMAR REDDY
 
LR(1) and SLR(1) parsing
byR Islam
 
Bottom - Up Parsing
bykunj desai
 
Compiler design syntax analysis
byRicha Sharma
 
Bottom up parser
byEsmeraldaAkshu1
 

What's hot

PPTX
RECURSIVE DESCENT PARSING
byJothi Lakshmi
 
PPTX
Lecture 14 run time environment
byIffat Anjum
 
PPTX
Lexical Analysis - Compiler Design
byAkhil Kaushik
 
PPTX
Three address code In Compiler Design
byShine Raj
 
PPTX
The role of the parser and Error recovery strategies ppt in compiler design
bySadia Akter
 
PPTX
Top down parsering and bottom up parsering.pptx
byLaibaFaisal3
 
PPTX
Pushdown Automata Theory
bySaifur Rahman
 
PPTX
A Role of Lexical Analyzer
byArchana Gopinath
 
PDF
Infix to postfix expression in ds
byRohini Mahajan
 
PPTX
Unit 3 sp assembler
byDeepmala Sharma
 
PPTX
Design of a two pass assembler
byDhananjaysinh Jhala
 
PPTX
10-SLR parser practice problems-02-06-2023.pptx
byvenkatapranaykumarGa
 
PDF
Operator precedence
byEsmeraldaAkshu1
 
PPTX
Relationship Among Token, Lexeme & Pattern
byBharat Rathore
 
PPTX
Top down and botttom up Parsing
byGerwin Ocsena
 
PPTX
First and follow set
byDawood Faheem Abbasi
 
PPT
Infix prefix postfix
bySelf-Employed
 
PDF
COMPILER DESIGN- Syntax Directed Translation
byJyothishmathi Institute of Technology and Science Karimnagar
 
PPTX
daa-unit-3-greedy method
byhodcsencet
 
PDF
Code generation in Compiler Design
byKuppusamy P
 
RECURSIVE DESCENT PARSING
byJothi Lakshmi
 
Lecture 14 run time environment
byIffat Anjum
 
Lexical Analysis - Compiler Design
byAkhil Kaushik
 
Three address code In Compiler Design
byShine Raj
 
The role of the parser and Error recovery strategies ppt in compiler design
bySadia Akter
 
Top down parsering and bottom up parsering.pptx
byLaibaFaisal3
 
Pushdown Automata Theory
bySaifur Rahman
 
A Role of Lexical Analyzer
byArchana Gopinath
 
Infix to postfix expression in ds
byRohini Mahajan
 
Unit 3 sp assembler
byDeepmala Sharma
 
Design of a two pass assembler
byDhananjaysinh Jhala
 
10-SLR parser practice problems-02-06-2023.pptx
byvenkatapranaykumarGa
 
Operator precedence
byEsmeraldaAkshu1
 
Relationship Among Token, Lexeme & Pattern
byBharat Rathore
 
Top down and botttom up Parsing
byGerwin Ocsena
 
First and follow set
byDawood Faheem Abbasi
 
Infix prefix postfix
bySelf-Employed
 
COMPILER DESIGN- Syntax Directed Translation
byJyothishmathi Institute of Technology and Science Karimnagar
 
daa-unit-3-greedy method
byhodcsencet
 
Code generation in Compiler Design
byKuppusamy P
 

Similar to Slr parser

PPTX
UNIT 2 (1).pptx
byAbhishek Tirkey
 
DOCX
11-SLR input string parsing, CLR introduction-06-06-2023.docx
byvenkatapranaykumarGa
 
PPTX
Compiler Deisgn-Varrious parsing methods
bycscprabh
 
PDF
LR0Examples.pdf LR(0) LR(1) it's my pres
byMuqadasWajid004
 
PPTX
Top Down Parsing, Predictive Parsing
byTanzeela_Hussain
 
PPT
PARSING.ppt
byayyankhanna6480086
 
PPTX
Parsing techniques, notations, methods of parsing in compiler design
bynithya g
 
PPT
Chapter 4 of Compiler Design - Syntax Analysis_2.ppt
bylatij10553
 
PPTX
Top down parsing
byLakshmiSamivel
 
PPTX
3. Syntax Analyzer.pptx
byMattupallipardhu
 
PPT
ch5-bottomupparser_jfdrhgfrfyyssf-gfrrt.PPT
byFutureTechnologies3
 
PPT
Compiler Construction - CS606 Power Point Slides Lecture 13.ppt
byZainabShahzad9
 
PPTX
Syntax Analysis - LR(0) Parsing in Compiler
byRizwanAbro4
 
PPTX
Syntax Analysis.pptx
byAshaS74
 
PDF
Theory of automata and formal language lab manual
byNitesh Dubey
 
PPT
Predicting Stock Market Trends Using Machine Learning and Deep Learning Algor...
bynakshpub
 
PPT
Chapter 4 - Syntax Analysis.ppt with the
bysubhankarg3
 
PPT
Parsing
bykhush_boo31
 
PPTX
4. CD- Unit2 - Predictive Parsers i.pptx
bybeaulah5219
 
PDF
LL(1) and the LR family of parsers used in compilers
byMandarMitra1
 
UNIT 2 (1).pptx
byAbhishek Tirkey
 
11-SLR input string parsing, CLR introduction-06-06-2023.docx
byvenkatapranaykumarGa
 
Compiler Deisgn-Varrious parsing methods
bycscprabh
 
LR0Examples.pdf LR(0) LR(1) it's my pres
byMuqadasWajid004
 
Top Down Parsing, Predictive Parsing
byTanzeela_Hussain
 
PARSING.ppt
byayyankhanna6480086
 
Parsing techniques, notations, methods of parsing in compiler design
bynithya g
 
Chapter 4 of Compiler Design - Syntax Analysis_2.ppt
bylatij10553
 
Top down parsing
byLakshmiSamivel
 
3. Syntax Analyzer.pptx
byMattupallipardhu
 
ch5-bottomupparser_jfdrhgfrfyyssf-gfrrt.PPT
byFutureTechnologies3
 
Compiler Construction - CS606 Power Point Slides Lecture 13.ppt
byZainabShahzad9
 
Syntax Analysis - LR(0) Parsing in Compiler
byRizwanAbro4
 
Syntax Analysis.pptx
byAshaS74
 
Theory of automata and formal language lab manual
byNitesh Dubey
 
Predicting Stock Market Trends Using Machine Learning and Deep Learning Algor...
bynakshpub
 
Chapter 4 - Syntax Analysis.ppt with the
bysubhankarg3
 
Parsing
bykhush_boo31
 
4. CD- Unit2 - Predictive Parsers i.pptx
bybeaulah5219
 
LL(1) and the LR family of parsers used in compilers
byMandarMitra1
 

More from Akila Krishnamoorthy

PPTX
Automata Theory - Turing machine
byAkila Krishnamoorthy
 
PPTX
Automata theory - RE to DFA Conversion
byAkila Krishnamoorthy
 
PPTX
Automata theory - Push Down Automata (PDA)
byAkila Krishnamoorthy
 
PPTX
Automata theory -RE to NFA-ε
byAkila Krishnamoorthy
 
PPTX
Automata theory - NFA ε to DFA Conversion
byAkila Krishnamoorthy
 
PPTX
Automata theory - NFA to DFA Conversion
byAkila Krishnamoorthy
 
PPTX
Automata theory -- NFA and DFA construction
byAkila Krishnamoorthy
 
PPTX
Intro to automata theory
byAkila Krishnamoorthy
 
PPTX
Automata theory -Conversion of ε nfa to nfa
byAkila Krishnamoorthy
 
PPTX
Automata theory - CFG and normal forms
byAkila Krishnamoorthy
 
PPTX
Linear data structure concepts
byAkila Krishnamoorthy
 
PPTX
Keypoints c strings
byAkila Krishnamoorthy
 
Automata Theory - Turing machine
byAkila Krishnamoorthy
 
Automata theory - RE to DFA Conversion
byAkila Krishnamoorthy
 
Automata theory - Push Down Automata (PDA)
byAkila Krishnamoorthy
 
Automata theory -RE to NFA-ε
byAkila Krishnamoorthy
 
Automata theory - NFA ε to DFA Conversion
byAkila Krishnamoorthy
 
Automata theory - NFA to DFA Conversion
byAkila Krishnamoorthy
 
Automata theory -- NFA and DFA construction
byAkila Krishnamoorthy
 
Intro to automata theory
byAkila Krishnamoorthy
 
Automata theory -Conversion of ε nfa to nfa
byAkila Krishnamoorthy
 
Automata theory - CFG and normal forms
byAkila Krishnamoorthy
 
Linear data structure concepts
byAkila Krishnamoorthy
 
Keypoints c strings
byAkila Krishnamoorthy
 

Recently uploaded

PPTX
Optimum mesh size for various fishing gears by B2B.pptx
byB. BHASKAR
 
PPTX
DIFFERENT TYPES OF SRTUCTURAL SYSTEM ANALYSIS
bynoshin231202
 
PPTX
[Deck] What's New in Spark-Iceberg Integration via DSV2.pptx
bySzehon Ho
 
PDF
PROBLEM SLOVING AND PYTHON PROGRAMMING UNIT 3.pdf
byA R SIVANESH M.E., QIP-PG (Cyber Security)., (Ph.D)
 
PPTX
Optimizing the ELBO Objective: A Comparative Study of RNN, LSTM, and GRU Arch...
byKayalvizhi A
 
PDF
Highway Curves in Transportation Engineering.pdf
byMahmoodKhalid11
 
PDF
Unit Weight in Term of Volumetric Water Content.pdf
byMahmoodKhalid11
 
PDF
Rajesh Prasad- Brief Profile with educational, professional highlights
byRajesh Prasad
 
PDF
engineering management chapter 5 ppt presentation
byericaangelatoledo06
 
PPTX
Why TPM Succeeds in Some Plants and Struggles in Others | MaintWiz
byMaintWiz Technologies Private Limited
 
PDF
Computer Network Lab Manual ssit -kavya r.pdf or Computer Network Lab Manual ...
bykavya R
 
PDF
Shear Strength of Soil (Direct shear test).pdf
byMahmoodKhalid11
 
PPTX
Fuel Injection Pump Test Bench – Precision Testing & Calibration for Diesel E...
byNeometrix_Engineering_Pvt_Ltd
 
PDF
Unit-I Process Management 1.9 Scheduling Criteria, Scheduling Algorithms
bySanjay Gunjal
 
PPTX
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
PPTX
Why Most SAP PM Implementations Fail — And How High-Reliability Plants Fix It
byMaintWiz Technologies Private Limited
 
PPTX
A professional presentation on Cosmos Bank Heist
byssuser7f0075
 
PDF
Microcontroller Notes Final 2016 April june.pdf
bypmuiruri768
 
PDF
DAA Lab Manual ssit -kavya r.pdf or Digital Design and Analysis of Algorithm ...
bykavya R
 
PDF
NS unit wise unit wise 1 -5 so prepare,.
bykumaransudhan1512
 
Optimum mesh size for various fishing gears by B2B.pptx
byB. BHASKAR
 
DIFFERENT TYPES OF SRTUCTURAL SYSTEM ANALYSIS
bynoshin231202
 
[Deck] What's New in Spark-Iceberg Integration via DSV2.pptx
bySzehon Ho
 
PROBLEM SLOVING AND PYTHON PROGRAMMING UNIT 3.pdf
byA R SIVANESH M.E., QIP-PG (Cyber Security)., (Ph.D)
 
Optimizing the ELBO Objective: A Comparative Study of RNN, LSTM, and GRU Arch...
byKayalvizhi A
 
Highway Curves in Transportation Engineering.pdf
byMahmoodKhalid11
 
Unit Weight in Term of Volumetric Water Content.pdf
byMahmoodKhalid11
 
Rajesh Prasad- Brief Profile with educational, professional highlights
byRajesh Prasad
 
engineering management chapter 5 ppt presentation
byericaangelatoledo06
 
Why TPM Succeeds in Some Plants and Struggles in Others | MaintWiz
byMaintWiz Technologies Private Limited
 
Computer Network Lab Manual ssit -kavya r.pdf or Computer Network Lab Manual ...
bykavya R
 
Shear Strength of Soil (Direct shear test).pdf
byMahmoodKhalid11
 
Fuel Injection Pump Test Bench – Precision Testing & Calibration for Diesel E...
byNeometrix_Engineering_Pvt_Ltd
 
Unit-I Process Management 1.9 Scheduling Criteria, Scheduling Algorithms
bySanjay Gunjal
 
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
Why Most SAP PM Implementations Fail — And How High-Reliability Plants Fix It
byMaintWiz Technologies Private Limited
 
A professional presentation on Cosmos Bank Heist
byssuser7f0075
 
Microcontroller Notes Final 2016 April june.pdf
bypmuiruri768
 
DAA Lab Manual ssit -kavya r.pdf or Digital Design and Analysis of Algorithm ...
bykavya R
 
NS unit wise unit wise 1 -5 so prepare,.
bykumaransudhan1512
 

Slr parser

  • 1.
    SLR PARSER Steps: 1. createaugment grammar 2. generate kernel items 3. find closure 4. compute goto() 5. construct parsing table 6. parse the string Let us consider grammar: S->a S->(L) L->S L->L,S
  • 2.
    • Step :1Create augment grammar S is start symbol in the given grammar Augment grammar is S’-> S • Step :2 Generate kernel items Introduce dot in RHS of the production`` S’-> .S • Step :3 Find closure (Rule: A -> α.Xβ i.e if there is nonterminal next to dot then Include X production)) S’-> .S S-> . a S->.(L) I0
  • 3.
    Step :4 computegoto() S’-> S . I1 Goto (I0,a) S-> a . I2 Goto (I0,( ) S’-> .S S-> . a S->.(L) I0 S-> (.L) L->.S L>.L,S S->.a S->.(L) I3 Goto (I3,L ) S-> (L .) L->L . ,S I4 Goto (I3,S ) L->S . I5 Goto (I3,a ) S->a . I2 Goto (I3, ( ) S-> (. L ) L->.S L>.L,S S->.a S->.(L) I3 Goto (I0,S)
  • 4.
    Goto (I4, )) S-> (L) . I6 Goto (I4, , ) L->L , . S S-> . a S->.(L) I7 Goto (I7,S ) L->L , S . I8 Goto (I7,a ) S-> a . I2 Goto (I7,( ) S-> (.L) L->.S L>.L,S S->.a S->.(L) I3 label Production Ending iteration R0 S’-> S . I1 R1 S->a . I2 R2 S->(L) . I6 R3 L->S . I5 R4 L->L,S . I8
  • 5.
    Step :5 constructparsing table Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols Terminals Non terminals a ( ) , $ S L 0 1 2 3 4 5 6 7 8
  • 6.
    Step :5 constructparsing table from step 4: Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 2 3 S2 S3 5 4 4 S6 S7 5 6 7 S2 S3 8 8 Goto (I0, S) 1 Goto (I3, ( ) 3 Goto (I0, a) 2 Goto (I4, ) ) 6 Goto (I0, ( ) 3 Goto (I4, ,) 7 Goto (I3, L) 4 Goto (I7, S) 8 Goto (I3, S) 5 Goto (I7, a) 2 Goto (I3, a) 2 Goto (I7, ( ) 3
  • 7.
    Step :5 constructparsing table Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 label Production Ending iteration Follow(LHS) R0 S’-> S . I1 Follow(S’)={ $ } R1 S-> a . I2 Follow(S)={ $ ) , } R2 S-> ( L ) . I6 Follow(S)={ $ ) , } R3 L-> S . I5 Follow(L)={ ) , } R4 L-> L , S . I8 Follow(L)={ ) , }
  • 8.
    Step :5 constructparsing table Label the rows of table with no. of iterations Divide the Column into two parts • Action part: terminal symbols • Goto part: Nonterminal symbols ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 label Production Ending iteration Follow(LHS) R0 S’-> S . I1 Follow(S’)={ $ } R1 S-> a . I2 Follow(S)={ $ ) , } R2 S-> ( L ) . I6 Follow(S)={ $ ) , } R3 L-> S . I5 Follow(L)={ ) , } R4 L-> L , S . I8 Follow(L)={ ) , } Goto (I0, S) 1 Goto (I3, ( ) 3 Goto (I0, a) 2 Goto (I4, ) ) 6 Goto (I0, ( ) 3 Goto (I4, ,) 7 Goto (I3, L) 4 Goto (I7, S) 8 Goto (I3, S) 5 Goto (I7, a) 2 Goto (I3, a) 2 Goto (I7, ( ) 3
  • 9.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 10.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 11.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 12.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 13.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 14.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 15.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 16.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 17.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 18.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 $0(3L4 ) $ S6 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 19.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 $0(3L4 ) $ S6 $0(3L4)6 $ R2 label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .
  • 20.
    Step :6 Stringparsing Let string w=(a,a) derived from the given grammar S – Shift action * shift input symbol to the stack * shift number to the stack R – Reduce action * pop 2 times of RHS symbols * shift LHS to the stack * find the number in the parsing table for the last two elements in the stack ACTION GOTO a ( ) , $ S L 0 S2 S3 1 1 accept 2 R1 R1 R1 3 S2 S3 5 4 4 S6 S7 5 R3 R3 6 R2 R2 R2 7 S2 S3 8 8 R4 R4 Stack Input Action $0 (a,a)$ S3 $0(3 a,a)$ S2 $0(3a2 ,a)$ R1 $0(3S5 ,a)$ R3 $0(3L4 ,a)$ S7 $0(3L4 , 7 a)$ S2 $0(3L4 , 7a2 )$ R1 $0(3L4 , 7S8 )$ R4 $0(3L4 ) $ S6 $0(3L4)6 $ R2 $0S1 $ accept Hence the string parsed successfully !!!!!! label Production R0 S’-> S . R1 S-> a . R2 S-> ( L ) . R3 L-> S . R4 L-> L , S .