Uploaded bynandepovanhu
PPT, PDF39 views

finitw automata2, Computer theory computure science

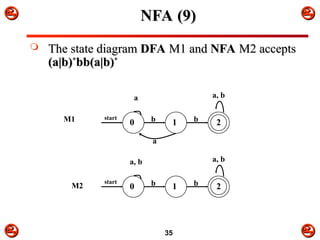
The document discusses finite automata, detailing both deterministic (DFA) and nondeterministic finite automata (NFA). It defines key concepts such as states, transitions, and acceptance conditions, illustrating how a DFA can be represented as a state diagram and how it processes input strings. Additionally, it highlights specific examples of languages accepted by DFAs and contrasts the characteristics of non-deterministic automata.

Embed presentation

Download to read offline
1         Chapter 2 Chapter 2 Finite Automata Finite Automata
        2 A Finite-State Machine (1) A Finite-State Machine (1)  A finite state machine is a mathematical model of a A finite state machine is a mathematical model of a system, with discrete inputs and outputs system, with discrete inputs and outputs
        3 A Finite-State Machine (2) A Finite-State Machine (2)  Finite Automata FA: Finite Automata FA:  a finite set of states  a set of transitions (edges)  a start state  a set of final states Defining a FA is a kind of programming. Defining a FA is a kind of programming.  Problem definition Problem definition  Includes defining possible actions & accepting condition.  States States   structure of program structure of program  Includes designating which are initial & final.  Transitions Transitions   program program
        4 2.1: Deterministic Finite Automata (1) 2.1: Deterministic Finite Automata (1)  DFA M = (Q, DFA M = (Q,  , ,  , , q q0 0, F) , F)  Q = a finite set of states  = a finite set called the alphabet  = transition function  total function Q    Q  q0 = start state q0  Q  F = final or accepting states F  Q
        5 Deterministic Finite Automata (2) Deterministic Finite Automata (2)  DFA M DFA M  Q = {q0, q1}  = {a, b}  F = {q1}  The transition function  is given in a tabular form called the transition table  (q0, a) = q1 (q0, b) = q0  (q1, a) = q1 (q1, b) = q0
        6 Deterministic Finite Automata (3) Deterministic Finite Automata (3)  A A DFA DFA M can be considered to be a language M can be considered to be a language acceptor. acceptor.  The The language language of M, of M, L(M) L(M), is the set of strings , is the set of strings  * * accepted by M. accepted by M.  A A DFA DFA M reads an input string from left to right. M reads an input string from left to right.  The The next state next state depends on the depends on the current state current state and and the the unread (unprocessed) symbol unread (unprocessed) symbol. .
        7 Deterministic Finite Automata (5) Deterministic Finite Automata (5)  The DFA The DFA M M accepts the set of strings over {a, b} that accepts the set of strings over {a, b} that contain the substring contain the substring bb bb  M : Q = {q0, q1, q2}, = {a, b}, F = {q2}  The transition function  is given in a tabular form called the transition table  (q0, a) = q0 (q0, b) = q1  (q1, a) = q0 (q1, b) = q2  (q2, a) = q2 (q2, b) = q2  Is Is abba abba   L(M)? Yes, since the computation halts in state L(M)? Yes, since the computation halts in state q q2 2, which is a final state , which is a final state  Is Is abab abab   L(M)? No, since the computation halts in state L(M)? No, since the computation halts in state q q1 1, which is , which is NOT NOT a final state a final state
        8 Deterministic Finite Automata (6) Deterministic Finite Automata (6)  Extended transition function Extended transition function  * * of a DFA with of a DFA with transition function transition function   is a function from Q is a function from Q    * *   Q Q defined recursively on the length of the input string defined recursively on the length of the input string w w  Basis: |w| = 0. Then w =  and * (qi, ) = qi  Recursive step: Let |w| = 1. Then * (qi, av) = * ((qi, a), v)   qi  Q,  a  ,  v  *
        9 Deterministic Finite Automata (7) Deterministic Finite Automata (7)  A string A string w w is accepted if is accepted if  * * (q (q0 0, , w w) )   F F  The language of a DFA The language of a DFA M M is is  L(M) = {w  * | * (q0, w)  F}  DFA M = (Q, DFA M = (Q,  , ,  , q , q0 0, F) accepts , F) accepts w w    * *    * (q0, w)  F
        10 Deterministic Finite Automata (8) Deterministic Finite Automata (8)  Two possibilities for DFA M running on Two possibilities for DFA M running on w w  M accepts w  M accepts w iff the computation of M on w ends up (halts) in an accepting configuration  * (q0, w)  F  M rejects w  M rejects w iff the computation of M on w ends up (halts) in a rejecting configuration  * (q0, w)  F
        11  The state diagram of a DFA M = The state diagram of a DFA M = (Q, (Q,  , ,  ,q ,q0 0, F) , F) is a is a labeled graph labeled graph G G defined by the following defined by the following conditions: conditions:  The nodes of G are the elements of Q  The labels on the arcs of G are elements of   q0 is the start node, denoted by  F is the set of accepting nodes, denoted by  There is an arc from node qi to qj labeled a if (qi, a) = qj  For every node qi and symbol a  , there is exactly one arc labeled a leaving qi State Diagrams and Examples (1) State Diagrams and Examples (1) q0 a
        12 State Diagrams and Examples (2) State Diagrams and Examples (2)  Deterministic Finite Automata DFA Deterministic Finite Automata DFA  all outgoing edges are labelled with an input character  no state has - transition, transition on input   no two edges leaving a given state have the same label  for each state s and input symbol a, there is at most one edge label a leaving s  Therefore: the next state can be determined uniquely, given the current state and the current input character
        13 State Diagrams and Examples (1) State Diagrams and Examples (1) strings over { strings over {a a, ,b b} with at least 3 } with at least 3 a a’s ’s 1 a 2 a 3+ a 0 a a a a b b b 
        14 State Diagrams and Examples (2) State Diagrams and Examples (2) strings over { strings over {a a, ,b b} with length mod 3 = 0 } with length mod 3 = 0 1 2 0   
        15 State Diagrams and Examples (3) State Diagrams and Examples (3) strings over { strings over {a a, ,b b} } without without 3 consecutive 3 consecutive a a’s ’s A simple example of “strings not of the form …”. A simple example of “strings not of the form …”. 1 a 2 a Has aaa 0 a a a a b b b 
        16 State Diagrams and Examples (4) State Diagrams and Examples (4)  Draw a state diagram for DFA Draw a state diagram for DFA M M that accepts the that accepts the set of strings over {a, b} that contain the substring set of strings over {a, b} that contain the substring bb bb  The string The string ababb ababb is accepted since the halting state is accepted since the halting state is the accepting state is the accepting state q q2 2 q1 q2 q0 b b a a a, b
        17 State Diagrams and Examples (5) State Diagrams and Examples (5)  The DFA The DFA  accepts ( accepts (b b| |ab ab) )* * ( (a a| | ) )  the set of strings over {a, b} that the set of strings over {a, b} that do not do not contain contain the substring the substring aa aa 1 a 2 a 0 a a a b b 
        18 State Diagrams and Examples (6) State Diagrams and Examples (6)  The language { The language {a an n b bn n , , n n 0} is not regular, so we can not 0} is not regular, so we can not build a DFA that accept this language build a DFA that accept this language  It needs an infinite number of states It needs an infinite number of states  But { But {a an n b bn n , 1 , 1   n n   3} is regular and its DFA is 3} is regular and its DFA is q0 a q1 a q2 a q3 q4 b q5 b b q6 b b This DFA is NOT Complete
        19 State Diagrams and Examples (7) State Diagrams and Examples (7)  strings over {a, b} that contain the substring strings over {a, b} that contain the substring bb bb OR OR do not do not contain the substring contain the substring aa aa  This language is the union of the languages of the This language is the union of the languages of the previous examples previous examples 1 a 2 a 0 a a a b a 1 b 2 b b b a  2 a b a b
        20 State Diagrams and Examples (8) State Diagrams and Examples (8)  strings over {a, b} that contain an strings over {a, b} that contain an even even number of number of a a’s ’s AND AND an an odd odd number of number of b b’s ’s [ea, eb] [ea, ob] a [oa, eb] [oa, ob] b a a a b b b
        21 State Diagrams and Examples (9) State Diagrams and Examples (9)  Let Let M M be the DFA previous slide be the DFA previous slide  A DFA A DFA M’ M’ that accepts all strings over {a, b} that that accepts all strings over {a, b} that do not do not contain an contain an even even number of number of a a’s ’s AND AND an an odd odd number of number of b b’s ’s is shown below is shown below  L(M’) = {a, b}* - L(M) = * - L(M)  Any string accepted by Any string accepted by M M is rejected by is rejected by M’ M’ and vice versa and vice versa [ea, eb] [ea, ob] a [oa, eb] [oa, ob] b a a a b b b
        22 State Diagrams and Examples (10) State Diagrams and Examples (10)  Let Let   = {0, 1, 2, 3}. A string in = {0, 1, 2, 3}. A string in  * * is a sequence of integers is a sequence of integers from from    The DFA The DFA M M determines whether the determines whether the sum of elements sum of elements of a of a string is string is divisible by 4 divisible by 4  The string The string 12302 12302 and and 0130 0130 should be accepted and should be accepted and 0111 0111 rejected by M rejected by M w mod 4 = 0 0 2 2 1 3 w mod 4 = 1 0 w mod 4 = 2 0 1 3 w mod 4 = 3 0 2 2 1 3 1 3
        23 State Diagrams and Examples (11) State Diagrams and Examples (11)  DFA DFA M1 M1 accepts accepts (ab) (ab)* * c c  M1 M1 is is incomplete determinism incomplete determinism  The string The string abcc abcc is is rejected rejected since since M1 M1 is unable to process is unable to process the final the final c c from state from state q q2 2 q0 q1 c q2 a b M1
        24 State Diagrams and Examples (12) State Diagrams and Examples (12)  M2 M2 accepts the same language as accepts the same language as M1 M1 in previous example in previous example (ab) (ab)* * c c  The state The state q qe e is the error state (dead end) is the error state (dead end) q0 q1 c q2 a b qe b a, c a, b, c M2 
        25 State Diagrams and Examples (13) State Diagrams and Examples (13) strings over { strings over {a a, ,b b} with next-to-last symbol = } with next-to-last symbol = a a …aa …ab a …ba …bb  a b b a b b b a a a a a b b b
        26 State Diagrams and Examples (14) State Diagrams and Examples (14) start 0 3 b 2 1 b a b a b a a What Language is Accepted?
        27 2.2: Nondeterministic Finite Automata (1) 2.2: Nondeterministic Finite Automata (1) Finite Automata : A recognizer that takes an input string & determines whether it’s a valid sentence of the language Non-Deterministic : Has more than one (or no) alternative action for the same input symbol. Deterministic : Has at most one action for every given input symbol.
        28 Nondeterministic Finite Automata (2) Nondeterministic Finite Automata (2) NFA: Formal Definition NFA: Formal Definition  NFA M = (Q, NFA M = (Q,  , ,  , q , q0 0, F) , F)  Q = a finite set of states  = a finite set alphabet  = transition function  total function Q    (Q) = 2Q - power set of Q  q0 = initial/starting state q0  Q  F = final or accepting states F  Q
        29 Nondeterministic Finite Automata (3) Nondeterministic Finite Automata (3) Q = { 0, 1, 2, 3 } q0 = 0 F = { 3 }  = { a, b } start 0 3 b 2 1 b a a b What Language is defined ? What is the Transition Table ? s t a t e i n p u t 0 1 2 a b { 0, 1 }  { 2 }  { 3 } { 0 }
        30 Nondeterministic Finite Automata (4) Nondeterministic Finite Automata (4)  Change in Change in    For an DFA M, (q, a) results in one and only one state for all states q and alphabet a  For an NFA M, (q, a) can result in a set of states, zero, one, or more states: qn a qi qn a qi qj qk a a qn  (q (qn n, a) = {q , a) = {qi i} }  (q (qn n, a) = {q , a) = {qi i, q , qj , j , q qk k } }  (q (qn n, a) = {} = , a) = {} =  
        31 Nondeterministic Finite Automata (5) Nondeterministic Finite Automata (5) 1 2 3 4 a a a b a,b a,b •Why is this only an NFA and not an DFA? 5
        32 Nondeterministic Finite Automata (6) Nondeterministic Finite Automata (6) Computing with NFA’s Computing with NFA’s  Computations are different Computations are different  We always start from start state. Call it the root of We always start from start state. Call it the root of the computation. the computation.  Then we might go to different states on one symbol. Then we might go to different states on one symbol.  Then from those states to new sets of states, Then from those states to new sets of states, creating a creating a tree-like tree-like computation. computation.  If one path ends up in a final state, then ACCEPT, If one path ends up in a final state, then ACCEPT, else REJECT else REJECT
        33 Nondeterministic Finite Automata (7) Nondeterministic Finite Automata (7) start 0 3 b 2 1 b a a b • Given an input string, we trace moves • If no more input & in final state, ACCEPT EXAMPLE: Input: ababb Path 1: 0 -> 0 -> 0 -> 0 -> 0 -> 0 (REJECT) Path 2: 0 -> 0 -> 0 -> 1 -> 2 -> 3 (ACCEPT)
        34 Nondeterministic Finite Automata (8) Nondeterministic Finite Automata (8)  Extended transition function Extended transition function  * * of a NFA with of a NFA with transition function transition function   is a function from Q is a function from Q    * *   2 2Q Q (power set) defined recursively on the length of (power set) defined recursively on the length of the input string the input string w w  Basis: |w| = 0. Then w =  and * (qi, ) = {qi}  Recursive step: Let |w| = 1. Then * (qi, av) = U * (qj, v), qj  (qi, a)   qi  Q,  qj  Q , a  ,  v *  The language of a NFA The language of a NFA M M is is  L(M) = {w  * | * (q0, w)  F ≠  }
        35 NFA (9) NFA (9)  The state diagram The state diagram DFA DFA M1 and M1 and NFA NFA M2 accepts M2 accepts (a|b) (a|b)* * bb(a|b) bb(a|b)* * a a, b start 0 2 1 b b a M1 start 0 2 1 b b a, b a, b M2
        36 NFA (10) NFA (10)  An NFA that accepts string over {a, b} with An NFA that accepts string over {a, b} with substring substring aa aa or or bb bb  There are 2 distinct acceptance paths for the string There are 2 distinct acceptance paths for the string abaaabb abaaabb start 0 2 1 a a a, b a, b 4 3 b b a, b
        37 NFA (11) NFA (11)  The state diagram The state diagram DFA DFA M1 and M1 and NFA NFA M2 accepts M2 accepts (a|b) (a|b)* * abba(a|b) abba(a|b)* * start 0 4 1 b a b a, b a M1 2 b 3 a a b start 0 4 1 b a a, b a, b M2 2 b 3 a
        38 NFA with NFA with -Transitions (1) -Transitions (1) NFA with NFA with  -transitions, denoted by NFA- -transitions, denoted by NFA-  Formal Definition Formal Definition  NFA- NFA-  M = (Q, M = (Q,  , ,  , q , q0 0, F) , F)  Q = a finite set of states  = a finite set alphabet  = transition function  total function Q  (  (Q)  q0 = initial/starting state q0  Q  F = final or accepting states F  Q   transitions j i   Switch state but do not use any input symbol
        39  -Transitions (2) -Transitions (2)  The input string The input string w w is accepted using is accepted using NFA- NFA-  if there if there is a computation that processes the is a computation that processes the entire string entire string and halts in an and halts in an accepting state accepting state  A computation may continue using A computation may continue using  -transition -transition after the input string has been completely after the input string has been completely processed processed
        40  -Transitions (3) -Transitions (3)  L(M L(M1 1) = (a|b) ) = (a|b)* * bb(a|b) bb(a|b)* * , L(M , L(M2 2) = (b|ab) ) = (b|ab)* * (a| (a| ) )  L(M) = L(M L(M) = L(M1 1) )   L(M L(M2 2) ) q1,1 q1,2 a, b b b q1,0 b a q2,0 0    a, b q2,1 b q1,1 q1,2 a, b b b q1,0 a, b b a q2,0 q2,1 b M1 M M2
        41  -Transitions (4) -Transitions (4)  L(M L(M1 1) = (a|b) ) = (a|b)* * bb(a|b) bb(a|b)* * , L(M , L(M2 2) = (b|ab) ) = (b|ab)* * (a| (a| ) )  L(M) = L(M L(M) = L(M1 1)L(M )L(M2 2) ) q1,1 q1,2 a, b b b q1,0 b a q2,0  a, b q2,1 b q1,1 q1,2 a, b b b q1,0 a, b b a q2,0 q2,1 b M1 M M2
        42  -Transitions (5) -Transitions (5)  M M accepts all strings over {a, b} of accepts all strings over {a, b} of even even length length q1 q2 a, b q0 a, b  
        43  -Transitions (6) -Transitions (6)  Let M Let M1 1 and M and M2 2 be 2 NFA- be 2 NFA- ’s as follows ’s as follows q1,0 q1,f M1 q2,0 q2,f M2 M1 = (Q1, , , q1,0, F1) M2 = (Q2, , , q2,0, F2)
        44  -Transitions (7) -Transitions (7)  L(M) = L(M L(M) = L(M1 1) )   L(M L(M2 2) ) q1,0 q1,f M1 q2,0 q2,f M2 q0   M = (Q1  Q2  {q0}, , , q0, F1  F2) is the same as in 1 and 2, but add: (q0, ) = {q1,0, q2,0}
        45  -Transitions (8) -Transitions (8)  L(M) = L(M L(M) = L(M1 1)L(M )L(M2 2) ) q1,0 q1,f M1 q2,0 q2,f M2  M = (Q1  Q2, , , q1,0, F2) is the same as in 1 and 2, but add: (q, ) = {q2,0}, where q  F1
        46  -Transitions (9) -Transitions (9)  L(M) = L(M L(M) = L(M1 1) )* * q1,0 q1,f M1  qf q0    M = (Q1  {q0, qf}, , , q0, {qf}) is the same as in 1, but add: (q0, ) = {q1,0 ,qf} (q1,f, ) = {q1,0 ,qf}, where q1,f F1
        47  -Transitions (10) -Transitions (10) Given the regular expression : a(b* c) | a( b | c+ | ) Find a transition diagram NFA-  that recognizes it.
        48  -Transitions (11) -Transitions (11) 3 2 b c a 1 6 5 7 c a c 4 b a (b* c) a( b | c+ | ) Now that you have the individual diagrams, “or” them as follows:
        49  -Transitions (12) -Transitions (12) 3 2 b c a 1 6 5 7 c a c 4 b 0  
        50  -Transitions (12) -Transitions (12)  See examples 2.7, 2.8, 2.9, and 2.10 See examples 2.7, 2.8, 2.9, and 2.10
        51 2.3: Equivalence of DFA & NFA (1) 2.3: Equivalence of DFA & NFA (1)  Is NFA more powerful than DFA? NO! Is NFA more powerful than DFA? NO!  NFA inefficient to implement directly, so convert to a DFA that recognizes the same strings  Is there a language accepted by an NFA that is not Is there a language accepted by an NFA that is not accepted by any DFA? No accepted by any DFA? No  NFA is equivalent to DFA. NFA is equivalent to DFA.  Each state in DFA corresponds to a SET of states of the NFA
        52 Removing Nondeterminism (2) Removing Nondeterminism (2)   -closure -closure  In an NFA- In an NFA- , the , the  -closure( -closure(q q) ) of a state of a state q q is the set is the set of all states that can be reached from of all states that can be reached from q q by by following a path whose edges are all labeled by following a path whose edges are all labeled by  . . q0 q1 q2 q3 b    a  b Start -closure(q0) = {q0, q1, q2, q3}  - -closure(q1) = {q1,q3}  - -closure(q2) = {q1,q2,q3}
        53 Removing Nondeterminism (3) Removing Nondeterminism (3) NFA- N = (Q, , , q0, F) -closure(q) : q  Q : set of NFA- states that are reachable from q on -transitions only -closure(T) : T  Q : NFA- states reachable from some state t  T on -transitions only move(T, a) : T  Q, a   : set of states to which there is a transition on input a from some state t  T move({q1, q2, …, qi}, a) = (q1, a)  (q2, a)  …  (qi, a) These 3 operations are utilized by algorithms / techniques to facilitate the conversion process No input is consumed
        54 Removing Nondeterminism (4) Removing Nondeterminism (4)  -closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0 on -moves)  -closure(0, 6) = -closure(0)  -closure(6) = {0, 1, 2, 4, 7}  {6, 1, 2, 4,7} = {0, 1, 2, 4, 6, 7}  move({0, 1, 2, 4, 7}, a) = {3, 8} (since move(2, a)=3 and move(7, a)=8) 0 1 2 3 5 4 6 7 8 9 10         a a b b b start
        55 NFA- NFA-   DFA DFA with Subset Construction with Subset Construction NFA- N  DFA M construction: Given N = (Q, , , q0, F), define M = (Q’, , ’, q’0, F’) Q’  P(Q), all the possible NFA- states M could be in. q’0 = -closure(q0) F’ = {q’  Q’ | q’  F  } ’(q’, a) = -closure(move(q’, a))  DFA M has a state ERR DFA M has a state ERR   Q’ = P(Q) Q’ = P(Q)  serves as the “error” state, when needed  ’(ERR, a) = ERR, a   By definition of ’
        56 Subset Construction Subset Construction Algorithm Concepts Algorithm Concepts First we calculate: -closure(0) (i.e., state 0) -closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0 on -moves) Let A = {0, 1, 2, 4, 7} be a state of new DFA M Start with NFA-: (a | b)*abb 0 1 2 3 5 4 6 7 8 9 10         a a b b b start
        57 Conversion Example (1) Conversion Example (1) b : -closure(move(A,b)) = -closure(move({0,1,2,4,7}, b)) adds {5} (since move(4, b) = 5) From this we have : -closure({5}) = {1,2,4,5,6,7} (since 5614, 67, and 12 all by -moves) Let C = {1,2,4,5,6,7} be a new state in D. Define M(A, b) = C 2nd , we calculate : a : -closure(move(A, a)) and b : -closure(move(A, b)) a : -closure(move(A, a)) = -closure(move({0,1,2,4,7}, a))} adds {3, 8} (since move(2, a) = 3 and move(7, a) = 8) From this we have : -closure({3, 8}) = {1,2,3,4,6,7,8} (since 3614, 67, and 12 all by -moves) Let B = {1,2,3,4,6,7,8} be a new state in D. Define M(A, a) = B
        58 Conversion Example (2) Conversion Example (2) 3rd , we calculate for state B on {a, b} a : -closure(move(B, a)) = -closure(move({1,2,3,4,6,7,8}, a))} = {1,2,3,4,6,7,8} = B Define M(B, a) = B b : -closure(move(B, b)) = -closure(move({1,2,3,4,6,7,8}, b))} = {1,2,4,5,6,7,9} = D Define M(B, b) = D 4th , we calculate for state C on {a, b} a : -closure(move(C, a)) = -closure(move({1,2,4,5,6,7}, a))} = {1,2,3,4,6,7,8} = B Define M(C, a) = B b : -closure(move(C, b)) = -closure(move({1,2,4,5,6,7}, b))} = {1,2,4,5,6,7} = C Define M(C, b) = C
        59 Conversion Example (3) Conversion Example (3) 5th , we calculate for state D on {a, b} a : -closure(move(D, a)) = -closure(move({1,2,4,5,6,7,9}, a))} = {1,2,3,4,6,7,8} = B Define M(D, a) = B b : -closure(move(D, b)) = -closure(move({1,2,4,5,6,7,9}, b))} = {1,2,4,5,6,7,10} = E Define M(D, b) = E Finally, we calculate for state E on {a, b} a : -closure(move(E, a)) = -closure(move({1,2,4,5,6,7,10}, a))} = {1,2,3,4,6,7,8} = B Define M(E, a) = B b : -closure(move(E, b)) = -closure(move({1,2,4,5,6,7,10}, b))} = {1,2,4,5,6,7} = C Define M(E, b) = C
        60 Conversion Example (4) Conversion Example (4) State Input Symbol a b A B C B B D C B C E B C D B E … A …b C …a B … abD … abbE start b b b b b a a a a This gives the transition table for the DFA M of: a
        61 Converting NFA- Converting NFA-  to DFA – 2 to DFA – 2nd nd Example Example 0 8 5 4 7 3 6 2 1               b a c   RE: c*(ab)*c* 1st we calculate: -closure(0) -closure(0) = {0, 1, 2, 6, 8} (all states reachable from 0 on -moves) Let A={0, 1, 2, 6, 8} be a state of new DFA M
        62 Conversion Example (1) Conversion Example (1) b : -closure(move(A,b)) = -closure(move({0,1,2,6,8}, b)) There is NO transition on b for all states 0,1,2,6 and 8 Define M(A, b) = Reject 2nd , we calculate : a : -closure(move(A, a)) and b : -closure(move(A, b)) c : -closure(move(A, c)) a : -closure(move(A, a)) = -closure(move({0,1,2,6,8}, a))} adds {3} (since move(2, a) = 3) From this we have : -closure({3}) = {3} (since 33 by -moves) Let B = {3} be a new state. Define M(A, a) = B c : -closure(move(A, c)) = -closure(move({0,1,2,6,8}, c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1,2,5,6,7,8} (since 758, 7512, and 7516 by -moves) Let C = {1,2,5,6,7,8} be a new state. Define M(A, c) = C
        63 Conversion Example (2) Conversion Example (2) b : -closure(move(B, b)) = -closure(move({3}, b)) adds {4} (since move(3, b) = 4) From this we have : -closure({4}) = {1,2,4,5,6,8} (since 458, 4512, and 4516 by -moves) Let D = {1,2,4,5,6,8} be a new state. Define M(B, b) = D 3rd , we calculate : a : -closure(move(B, a)) and b : -closure(move(B, b)) c : -closure(move(B, c)) a : -closure(move(B, a)) = -cclosure(move({3}, a))} There is NO transition on a for state 3 Define M(B, a) = Reject c : -closure(move(B, c)) = -closure(move({3}, c)) There is NO transition on c for state 3 Define M(B, c) = Reject
        64 Conversion Example (3) Conversion Example (3) b : -closure(move(C, b)) = -closure(move({1,2,5,6,7,8},b)) There is NO transition on b for all states 1,2,5,6, and 7 Define M(C, b) = Reject 4th , we calculate : a : -closure(move(C, a)) and b : -closure(move(C, b)) c : -closure(move(C, c)) a : -cclosure(move(C, a)) = -closure(move({1,2,5,6,7,8},a))} adds {3} (since move(2, a) = 3) -closure({3}) = {3} Define M(C, a) = B c : -closure(move(C, c)) = -closure(move({1,2,5,6,7,8},c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1,2,5,6,7,8} (since 758, 7512, and 7516 by -moves) Define M(C, c) = C
        65 Conversion Example (4) Conversion Example (4) b : -closure(move(D, b)) = -closure(move({1,2,4,5,6,8}, b)) There is NO transition on b for all states 1,2,4,5,6, and 8 Define M(D, b) = Reject 5th , we calculate : a : -closure(move(D, a)) and b : -closure(move(D, b)) c : -closure(move(D, c)) a : -closure(move(D, a)) = -closure(move({1,2,4,5,6,8},a))} adds {3} (since move(2, a) = 3) -closure({3}) = {3} Define M(D, a) = B c : -closure(move(D, c)) = -closure(move({1,2,4,5,6,8},c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1,2,5,6,7,8} (since 758, 7512, and 7516 by -moves) Define M(D, c) = C
        66 The Resulting DFA M The Resulting DFA M Which States are FINAL States ? 1, 2, 5, 6, 7, 8 1, 2, 4, 5, 6, 8 0, 1, 2, 6, 8 3 c b a a a c c D C A B c b a a a c c
        67 NFA- NFA-    DFA: Example DFA: Example strings over {a,b} with next-to-last symbol = a a a/b a/b q2 q1 q0  a b  q0 {q0, q1} {q0}  q1 {q2} {q2}  q2    M = ({q0, q1, q2}, {a,b}, , q0, {q2}) q0 q2 q0 q0 q1 q0 q1 q2 a a a a b b b b Equivalent DFA Equivalent DFA
        68 An Example of NFA- An Example of NFA-    DFA DFA Consider a simple NFA: Consider a simple NFA: Construct a corresponding DFA: Construct a corresponding DFA: 0 1 1 Start 0 1 q0 q1 {q0} {q0, q1} {q1} ERR ERR Start 1 0 1 0 1,0 1,0
        69 Examples Examples  See examples 2.11, 2.12, and 2.13 See examples 2.11, 2.12, and 2.13
        70 Class Discussion Class Discussion Construct a DFA equivalent to this NFA: Construct a DFA equivalent to this NFA: Start 0,1 q0 q1 0 q2 1 {q0, q1} Start 1 {q0} 0 1 {q0,q2} 0 1 0 0
        71 b a,b,c An NFA a 1 2 a 0 b,c c start Notice that the state with label {0, 1, 2} is from the set of states given by the nondeterministic transition (0, a) = {0, 1, 2}. Also notice that any state whose label contains an accepting state is defined as an accepting state in the deterministic machine. {0,1,2} {2} a a {1,2} b c b c c Converted DFA 0 start b,c Class Discussion Class Discussion
        72 2.4 Reduction of the Number of States in FA 2.4 Reduction of the Number of States in FA  Self study Self study  but not included in the exams material

More Related Content

PPT
Finite automata
byBipul Roy Bpl
 
PPTX
Week 3 - to FiniteAutomata DrJunaid.pptx
byMFaizan35
 
PPT
Finite Automata for CSE Engineering student
byimamenure
 
PPTX
finiteautomata-160104102657.pptx
byStudyvAbhi
 
PPT
Lecture 1 CSE 322 LPU By 5th SEM .ppt Good
byabcxyz19691969
 
PDF
02 Chapter Two-Finite Automata anx examples
bykbs33223
 
PPT
CSE-322 lecture1 notes
bydatabydevang
 
PPTX
Theory of Automata(Formal Language) Lecture 3.pptx
bymuhammadanasgc
 
Finite automata
byBipul Roy Bpl
 
Week 3 - to FiniteAutomata DrJunaid.pptx
byMFaizan35
 
Finite Automata for CSE Engineering student
byimamenure
 
finiteautomata-160104102657.pptx
byStudyvAbhi
 
Lecture 1 CSE 322 LPU By 5th SEM .ppt Good
byabcxyz19691969
 
02 Chapter Two-Finite Automata anx examples
bykbs33223
 
CSE-322 lecture1 notes
bydatabydevang
 
Theory of Automata(Formal Language) Lecture 3.pptx
bymuhammadanasgc
 

Similar to finitw automata2, Computer theory computure science

PPTX
DIU_BD_AvaGandu_SE-234-Lecture-02-DFA.pptx
bymafen98815
 
PPTX
AUTOMATA THEORY AUTOMATA THEORYAutomata3Chapter2.pptx
byArjayBalberan1
 
PDF
Lecture Two.pdf computer skills first lec
byzhwanmohammed4
 
PPTX
LectIntroduction to Finite Automata.pptx
bykennethnamonye77
 
PDF
Automata
byJena Catherine Bel D
 
PPTX
chapter 1 automata and complexity theory lecture note.pptx
byanwarkade1
 
PPTX
INTRODUTION Formal Language and Automatic Theory.pptx
bySUNEEL37
 
PPTX
FiniteAutomata_anim.pptx
byamara jyothi
 
PPTX
FiniteAutomata_anim.pptx
byranjan317165
 
PDF
Finite Automata
byA. S. M. Shafi
 
PPTX
CT_Sec_1.pptxfyocyococoycxoycyocycoyxykx6x
byuossryelshall
 
PPT
Finite Automata
byparmeet834
 
PDF
flat unit1
byJanhavi Vishwanath
 
PPT
Finite automata examples
byankitamakin
 
PPT
Finite automata examples
byankitamakin
 
PPT
FiniteAutomata-DFA and NFA from Theory of Computation.ppt
byAdharshKumarSingh
 
PPTX
TCS MUBAI UNIVERSITY ATHARVA COLLEGE OF ENGINEERING.pptx
byuserqwerty2612
 
PPTX
Chapter-twoChapter-three automata and complexity theory .pptx
byanwarkade1
 
PPTX
symbolic_automata or Advanced Programming Practice.pptx
bysudharsr
 
PDF
TCS GOLDEN NOTES THEORY OF COMPUTATION .pdf
byuserqwerty2612
 
DIU_BD_AvaGandu_SE-234-Lecture-02-DFA.pptx
bymafen98815
 
AUTOMATA THEORY AUTOMATA THEORYAutomata3Chapter2.pptx
byArjayBalberan1
 
Lecture Two.pdf computer skills first lec
byzhwanmohammed4
 
LectIntroduction to Finite Automata.pptx
bykennethnamonye77
 
Automata
byJena Catherine Bel D
 
chapter 1 automata and complexity theory lecture note.pptx
byanwarkade1
 
INTRODUTION Formal Language and Automatic Theory.pptx
bySUNEEL37
 
FiniteAutomata_anim.pptx
byamara jyothi
 
FiniteAutomata_anim.pptx
byranjan317165
 
Finite Automata
byA. S. M. Shafi
 
CT_Sec_1.pptxfyocyococoycxoycyocycoyxykx6x
byuossryelshall
 
Finite Automata
byparmeet834
 
flat unit1
byJanhavi Vishwanath
 
Finite automata examples
byankitamakin
 
Finite automata examples
byankitamakin
 
FiniteAutomata-DFA and NFA from Theory of Computation.ppt
byAdharshKumarSingh
 
TCS MUBAI UNIVERSITY ATHARVA COLLEGE OF ENGINEERING.pptx
byuserqwerty2612
 
Chapter-twoChapter-three automata and complexity theory .pptx
byanwarkade1
 
symbolic_automata or Advanced Programming Practice.pptx
bysudharsr
 
TCS GOLDEN NOTES THEORY OF COMPUTATION .pdf
byuserqwerty2612
 

Recently uploaded

PPTX
Differences between Patching and Extending components in Odoo 17
byCeline George
 
PPTX
History in your Hands Class 5 January 2026 online slides.pptx
byEilsONeill
 
PDF
Application of ICT lecture 4 ICT in Health and Well-being.pdf
byKhalil Khan Marwat
 
PPTX
Mixing Pharmaceutical Engineering .pptxx
byShraddha Bandgar
 
PPTX
OverView of AI in Products in Odoo 19
byCeline George
 
PPTX
Shipping Policies & Picking Policies in Odoo 18 Inventory
byCeline George
 
PPTX
SIZE REDUCTION Prepared By: Ms. Vaishnavi Ghormade
byvaishnavighormade199
 
PPTX
ANTI- RHEUMATICS CHAPTER NO.05 PHARMACOGNOSY
byGanu Gavade
 
PDF
Profiling, Placement, Pathways, and Pedagogies.pdf
byRHEAMARIMLA2
 
PPTX
Java Programming_BJD_Slideshare-Introduction.pptx
byBapusahebDange
 
PPTX
How to Manage Sorting Cart by Category in Odoo 18 POS
byCeline George
 
PPTX
Throat painting and throat swab.....pptx
byAneetaSharma15
 
PDF
Application of Information and Communication Technology Content.pdf
byKhalil Khan Marwat
 
PPTX
CHAPTER NO. 09 HCP BY GG LABORATORY CLINICAL TEST
byGanu Gavade
 
PPTX
Prepositions of Place : English Grammar Presentation
byPintoo Dhillon
 
PPTX
INSTAGRAM: Where Moment Turns Into Stories.pptx
byandriemark51
 
PPTX
How to add bank Account in Odoo 19
byCeline George
 
PDF
First Semester BCA Exam 2025 – Constitution Values – 1 Solved Answers.pdf
byKuvempu University
 
PPTX
CHAPTER NO. 05 DIURETICS PHARMACOGNOSY.pptx
byGanu Gavade
 
PPTX
How to use sorted() method in Odoo 18
byCeline George
 
Differences between Patching and Extending components in Odoo 17
byCeline George
 
History in your Hands Class 5 January 2026 online slides.pptx
byEilsONeill
 
Application of ICT lecture 4 ICT in Health and Well-being.pdf
byKhalil Khan Marwat
 
Mixing Pharmaceutical Engineering .pptxx
byShraddha Bandgar
 
OverView of AI in Products in Odoo 19
byCeline George
 
Shipping Policies & Picking Policies in Odoo 18 Inventory
byCeline George
 
SIZE REDUCTION Prepared By: Ms. Vaishnavi Ghormade
byvaishnavighormade199
 
ANTI- RHEUMATICS CHAPTER NO.05 PHARMACOGNOSY
byGanu Gavade
 
Profiling, Placement, Pathways, and Pedagogies.pdf
byRHEAMARIMLA2
 
Java Programming_BJD_Slideshare-Introduction.pptx
byBapusahebDange
 
How to Manage Sorting Cart by Category in Odoo 18 POS
byCeline George
 
Throat painting and throat swab.....pptx
byAneetaSharma15
 
Application of Information and Communication Technology Content.pdf
byKhalil Khan Marwat
 
CHAPTER NO. 09 HCP BY GG LABORATORY CLINICAL TEST
byGanu Gavade
 
Prepositions of Place : English Grammar Presentation
byPintoo Dhillon
 
INSTAGRAM: Where Moment Turns Into Stories.pptx
byandriemark51
 
How to add bank Account in Odoo 19
byCeline George
 
First Semester BCA Exam 2025 – Constitution Values – 1 Solved Answers.pdf
byKuvempu University
 
CHAPTER NO. 05 DIURETICS PHARMACOGNOSY.pptx
byGanu Gavade
 
How to use sorted() method in Odoo 18
byCeline George
 

finitw automata2, Computer theory computure science

  • 1.
    1         Chapter 2 Chapter2 Finite Automata Finite Automata
  • 2.
            2 A Finite-StateMachine (1) A Finite-State Machine (1)  A finite state machine is a mathematical model of a A finite state machine is a mathematical model of a system, with discrete inputs and outputs system, with discrete inputs and outputs
  • 3.
            3 A Finite-StateMachine (2) A Finite-State Machine (2)  Finite Automata FA: Finite Automata FA:  a finite set of states  a set of transitions (edges)  a start state  a set of final states Defining a FA is a kind of programming. Defining a FA is a kind of programming.  Problem definition Problem definition  Includes defining possible actions & accepting condition.  States States   structure of program structure of program  Includes designating which are initial & final.  Transitions Transitions   program program
  • 4.
            4 2.1: DeterministicFinite Automata (1) 2.1: Deterministic Finite Automata (1)  DFA M = (Q, DFA M = (Q,  , ,  , , q q0 0, F) , F)  Q = a finite set of states  = a finite set called the alphabet  = transition function  total function Q    Q  q0 = start state q0  Q  F = final or accepting states F  Q
  • 5.
            5 Deterministic FiniteAutomata (2) Deterministic Finite Automata (2)  DFA M DFA M  Q = {q0, q1}  = {a, b}  F = {q1}  The transition function  is given in a tabular form called the transition table  (q0, a) = q1 (q0, b) = q0  (q1, a) = q1 (q1, b) = q0
  • 6.
            6 Deterministic FiniteAutomata (3) Deterministic Finite Automata (3)  A A DFA DFA M can be considered to be a language M can be considered to be a language acceptor. acceptor.  The The language language of M, of M, L(M) L(M), is the set of strings , is the set of strings  * * accepted by M. accepted by M.  A A DFA DFA M reads an input string from left to right. M reads an input string from left to right.  The The next state next state depends on the depends on the current state current state and and the the unread (unprocessed) symbol unread (unprocessed) symbol. .
  • 7.
            7 Deterministic FiniteAutomata (5) Deterministic Finite Automata (5)  The DFA The DFA M M accepts the set of strings over {a, b} that accepts the set of strings over {a, b} that contain the substring contain the substring bb bb  M : Q = {q0, q1, q2}, = {a, b}, F = {q2}  The transition function  is given in a tabular form called the transition table  (q0, a) = q0 (q0, b) = q1  (q1, a) = q0 (q1, b) = q2  (q2, a) = q2 (q2, b) = q2  Is Is abba abba   L(M)? Yes, since the computation halts in state L(M)? Yes, since the computation halts in state q q2 2, which is a final state , which is a final state  Is Is abab abab   L(M)? No, since the computation halts in state L(M)? No, since the computation halts in state q q1 1, which is , which is NOT NOT a final state a final state
  • 8.
            8 Deterministic FiniteAutomata (6) Deterministic Finite Automata (6)  Extended transition function Extended transition function  * * of a DFA with of a DFA with transition function transition function   is a function from Q is a function from Q    * *   Q Q defined recursively on the length of the input string defined recursively on the length of the input string w w  Basis: |w| = 0. Then w =  and * (qi, ) = qi  Recursive step: Let |w| = 1. Then * (qi, av) = * ((qi, a), v)   qi  Q,  a  ,  v  *
  • 9.
            9 Deterministic FiniteAutomata (7) Deterministic Finite Automata (7)  A string A string w w is accepted if is accepted if  * * (q (q0 0, , w w) )   F F  The language of a DFA The language of a DFA M M is is  L(M) = {w  * | * (q0, w)  F}  DFA M = (Q, DFA M = (Q,  , ,  , q , q0 0, F) accepts , F) accepts w w    * *    * (q0, w)  F
  • 10.
            10 Deterministic FiniteAutomata (8) Deterministic Finite Automata (8)  Two possibilities for DFA M running on Two possibilities for DFA M running on w w  M accepts w  M accepts w iff the computation of M on w ends up (halts) in an accepting configuration  * (q0, w)  F  M rejects w  M rejects w iff the computation of M on w ends up (halts) in a rejecting configuration  * (q0, w)  F
  • 11.
            11  Thestate diagram of a DFA M = The state diagram of a DFA M = (Q, (Q,  , ,  ,q ,q0 0, F) , F) is a is a labeled graph labeled graph G G defined by the following defined by the following conditions: conditions:  The nodes of G are the elements of Q  The labels on the arcs of G are elements of   q0 is the start node, denoted by  F is the set of accepting nodes, denoted by  There is an arc from node qi to qj labeled a if (qi, a) = qj  For every node qi and symbol a  , there is exactly one arc labeled a leaving qi State Diagrams and Examples (1) State Diagrams and Examples (1) q0 a
  • 12.
            12 State Diagramsand Examples (2) State Diagrams and Examples (2)  Deterministic Finite Automata DFA Deterministic Finite Automata DFA  all outgoing edges are labelled with an input character  no state has - transition, transition on input   no two edges leaving a given state have the same label  for each state s and input symbol a, there is at most one edge label a leaving s  Therefore: the next state can be determined uniquely, given the current state and the current input character
  • 13.
            13 State Diagramsand Examples (1) State Diagrams and Examples (1) strings over { strings over {a a, ,b b} with at least 3 } with at least 3 a a’s ’s 1 a 2 a 3+ a 0 a a a a b b b 
  • 14.
            14 State Diagramsand Examples (2) State Diagrams and Examples (2) strings over { strings over {a a, ,b b} with length mod 3 = 0 } with length mod 3 = 0 1 2 0   
  • 15.
            15 State Diagramsand Examples (3) State Diagrams and Examples (3) strings over { strings over {a a, ,b b} } without without 3 consecutive 3 consecutive a a’s ’s A simple example of “strings not of the form …”. A simple example of “strings not of the form …”. 1 a 2 a Has aaa 0 a a a a b b b 
  • 16.
            16 State Diagramsand Examples (4) State Diagrams and Examples (4)  Draw a state diagram for DFA Draw a state diagram for DFA M M that accepts the that accepts the set of strings over {a, b} that contain the substring set of strings over {a, b} that contain the substring bb bb  The string The string ababb ababb is accepted since the halting state is accepted since the halting state is the accepting state is the accepting state q q2 2 q1 q2 q0 b b a a a, b
  • 17.
            17 State Diagramsand Examples (5) State Diagrams and Examples (5)  The DFA The DFA  accepts ( accepts (b b| |ab ab) )* * ( (a a| | ) )  the set of strings over {a, b} that the set of strings over {a, b} that do not do not contain contain the substring the substring aa aa 1 a 2 a 0 a a a b b 
  • 18.
            18 State Diagramsand Examples (6) State Diagrams and Examples (6)  The language { The language {a an n b bn n , , n n 0} is not regular, so we can not 0} is not regular, so we can not build a DFA that accept this language build a DFA that accept this language  It needs an infinite number of states It needs an infinite number of states  But { But {a an n b bn n , 1 , 1   n n   3} is regular and its DFA is 3} is regular and its DFA is q0 a q1 a q2 a q3 q4 b q5 b b q6 b b This DFA is NOT Complete
  • 19.
            19 State Diagramsand Examples (7) State Diagrams and Examples (7)  strings over {a, b} that contain the substring strings over {a, b} that contain the substring bb bb OR OR do not do not contain the substring contain the substring aa aa  This language is the union of the languages of the This language is the union of the languages of the previous examples previous examples 1 a 2 a 0 a a a b a 1 b 2 b b b a  2 a b a b
  • 20.
            20 State Diagramsand Examples (8) State Diagrams and Examples (8)  strings over {a, b} that contain an strings over {a, b} that contain an even even number of number of a a’s ’s AND AND an an odd odd number of number of b b’s ’s [ea, eb] [ea, ob] a [oa, eb] [oa, ob] b a a a b b b
  • 21.
            21 State Diagramsand Examples (9) State Diagrams and Examples (9)  Let Let M M be the DFA previous slide be the DFA previous slide  A DFA A DFA M’ M’ that accepts all strings over {a, b} that that accepts all strings over {a, b} that do not do not contain an contain an even even number of number of a a’s ’s AND AND an an odd odd number of number of b b’s ’s is shown below is shown below  L(M’) = {a, b}* - L(M) = * - L(M)  Any string accepted by Any string accepted by M M is rejected by is rejected by M’ M’ and vice versa and vice versa [ea, eb] [ea, ob] a [oa, eb] [oa, ob] b a a a b b b
  • 22.
            22 State Diagramsand Examples (10) State Diagrams and Examples (10)  Let Let   = {0, 1, 2, 3}. A string in = {0, 1, 2, 3}. A string in  * * is a sequence of integers is a sequence of integers from from    The DFA The DFA M M determines whether the determines whether the sum of elements sum of elements of a of a string is string is divisible by 4 divisible by 4  The string The string 12302 12302 and and 0130 0130 should be accepted and should be accepted and 0111 0111 rejected by M rejected by M w mod 4 = 0 0 2 2 1 3 w mod 4 = 1 0 w mod 4 = 2 0 1 3 w mod 4 = 3 0 2 2 1 3 1 3
  • 23.
            23 State Diagramsand Examples (11) State Diagrams and Examples (11)  DFA DFA M1 M1 accepts accepts (ab) (ab)* * c c  M1 M1 is is incomplete determinism incomplete determinism  The string The string abcc abcc is is rejected rejected since since M1 M1 is unable to process is unable to process the final the final c c from state from state q q2 2 q0 q1 c q2 a b M1
  • 24.
            24 State Diagramsand Examples (12) State Diagrams and Examples (12)  M2 M2 accepts the same language as accepts the same language as M1 M1 in previous example in previous example (ab) (ab)* * c c  The state The state q qe e is the error state (dead end) is the error state (dead end) q0 q1 c q2 a b qe b a, c a, b, c M2 
  • 25.
            25 State Diagramsand Examples (13) State Diagrams and Examples (13) strings over { strings over {a a, ,b b} with next-to-last symbol = } with next-to-last symbol = a a …aa …ab a …ba …bb  a b b a b b b a a a a a b b b
  • 26.
            26 State Diagramsand Examples (14) State Diagrams and Examples (14) start 0 3 b 2 1 b a b a b a a What Language is Accepted?
  • 27.
            27 2.2: NondeterministicFinite Automata (1) 2.2: Nondeterministic Finite Automata (1) Finite Automata : A recognizer that takes an input string & determines whether it’s a valid sentence of the language Non-Deterministic : Has more than one (or no) alternative action for the same input symbol. Deterministic : Has at most one action for every given input symbol.
  • 28.
            28 Nondeterministic FiniteAutomata (2) Nondeterministic Finite Automata (2) NFA: Formal Definition NFA: Formal Definition  NFA M = (Q, NFA M = (Q,  , ,  , q , q0 0, F) , F)  Q = a finite set of states  = a finite set alphabet  = transition function  total function Q    (Q) = 2Q - power set of Q  q0 = initial/starting state q0  Q  F = final or accepting states F  Q
  • 29.
            29 Nondeterministic FiniteAutomata (3) Nondeterministic Finite Automata (3) Q = { 0, 1, 2, 3 } q0 = 0 F = { 3 }  = { a, b } start 0 3 b 2 1 b a a b What Language is defined ? What is the Transition Table ? s t a t e i n p u t 0 1 2 a b { 0, 1 }  { 2 }  { 3 } { 0 }
  • 30.
            30 Nondeterministic FiniteAutomata (4) Nondeterministic Finite Automata (4)  Change in Change in    For an DFA M, (q, a) results in one and only one state for all states q and alphabet a  For an NFA M, (q, a) can result in a set of states, zero, one, or more states: qn a qi qn a qi qj qk a a qn  (q (qn n, a) = {q , a) = {qi i} }  (q (qn n, a) = {q , a) = {qi i, q , qj , j , q qk k } }  (q (qn n, a) = {} = , a) = {} =  
  • 31.
            31 Nondeterministic FiniteAutomata (5) Nondeterministic Finite Automata (5) 1 2 3 4 a a a b a,b a,b •Why is this only an NFA and not an DFA? 5
  • 32.
            32 Nondeterministic FiniteAutomata (6) Nondeterministic Finite Automata (6) Computing with NFA’s Computing with NFA’s  Computations are different Computations are different  We always start from start state. Call it the root of We always start from start state. Call it the root of the computation. the computation.  Then we might go to different states on one symbol. Then we might go to different states on one symbol.  Then from those states to new sets of states, Then from those states to new sets of states, creating a creating a tree-like tree-like computation. computation.  If one path ends up in a final state, then ACCEPT, If one path ends up in a final state, then ACCEPT, else REJECT else REJECT
  • 33.
            33 Nondeterministic FiniteAutomata (7) Nondeterministic Finite Automata (7) start 0 3 b 2 1 b a a b • Given an input string, we trace moves • If no more input & in final state, ACCEPT EXAMPLE: Input: ababb Path 1: 0 -> 0 -> 0 -> 0 -> 0 -> 0 (REJECT) Path 2: 0 -> 0 -> 0 -> 1 -> 2 -> 3 (ACCEPT)
  • 34.
            34 Nondeterministic FiniteAutomata (8) Nondeterministic Finite Automata (8)  Extended transition function Extended transition function  * * of a NFA with of a NFA with transition function transition function   is a function from Q is a function from Q    * *   2 2Q Q (power set) defined recursively on the length of (power set) defined recursively on the length of the input string the input string w w  Basis: |w| = 0. Then w =  and * (qi, ) = {qi}  Recursive step: Let |w| = 1. Then * (qi, av) = U * (qj, v), qj  (qi, a)   qi  Q,  qj  Q , a  ,  v *  The language of a NFA The language of a NFA M M is is  L(M) = {w  * | * (q0, w)  F ≠  }
  • 35.
            35 NFA (9) NFA(9)  The state diagram The state diagram DFA DFA M1 and M1 and NFA NFA M2 accepts M2 accepts (a|b) (a|b)* * bb(a|b) bb(a|b)* * a a, b start 0 2 1 b b a M1 start 0 2 1 b b a, b a, b M2
  • 36.
            36 NFA (10) NFA(10)  An NFA that accepts string over {a, b} with An NFA that accepts string over {a, b} with substring substring aa aa or or bb bb  There are 2 distinct acceptance paths for the string There are 2 distinct acceptance paths for the string abaaabb abaaabb start 0 2 1 a a a, b a, b 4 3 b b a, b
  • 37.
            37 NFA (11) NFA(11)  The state diagram The state diagram DFA DFA M1 and M1 and NFA NFA M2 accepts M2 accepts (a|b) (a|b)* * abba(a|b) abba(a|b)* * start 0 4 1 b a b a, b a M1 2 b 3 a a b start 0 4 1 b a a, b a, b M2 2 b 3 a
  • 38.
            38 NFA with NFAwith -Transitions (1) -Transitions (1) NFA with NFA with  -transitions, denoted by NFA- -transitions, denoted by NFA-  Formal Definition Formal Definition  NFA- NFA-  M = (Q, M = (Q,  , ,  , q , q0 0, F) , F)  Q = a finite set of states  = a finite set alphabet  = transition function  total function Q  (  (Q)  q0 = initial/starting state q0  Q  F = final or accepting states F  Q   transitions j i   Switch state but do not use any input symbol
  • 39.
            39  -Transitions (2) -Transitions(2)  The input string The input string w w is accepted using is accepted using NFA- NFA-  if there if there is a computation that processes the is a computation that processes the entire string entire string and halts in an and halts in an accepting state accepting state  A computation may continue using A computation may continue using  -transition -transition after the input string has been completely after the input string has been completely processed processed
  • 40.
            40  -Transitions (3) -Transitions(3)  L(M L(M1 1) = (a|b) ) = (a|b)* * bb(a|b) bb(a|b)* * , L(M , L(M2 2) = (b|ab) ) = (b|ab)* * (a| (a| ) )  L(M) = L(M L(M) = L(M1 1) )   L(M L(M2 2) ) q1,1 q1,2 a, b b b q1,0 b a q2,0 0    a, b q2,1 b q1,1 q1,2 a, b b b q1,0 a, b b a q2,0 q2,1 b M1 M M2
  • 41.
            41  -Transitions (4) -Transitions(4)  L(M L(M1 1) = (a|b) ) = (a|b)* * bb(a|b) bb(a|b)* * , L(M , L(M2 2) = (b|ab) ) = (b|ab)* * (a| (a| ) )  L(M) = L(M L(M) = L(M1 1)L(M )L(M2 2) ) q1,1 q1,2 a, b b b q1,0 b a q2,0  a, b q2,1 b q1,1 q1,2 a, b b b q1,0 a, b b a q2,0 q2,1 b M1 M M2
  • 42.
            42  -Transitions (5) -Transitions(5)  M M accepts all strings over {a, b} of accepts all strings over {a, b} of even even length length q1 q2 a, b q0 a, b  
  • 43.
            43  -Transitions (6) -Transitions(6)  Let M Let M1 1 and M and M2 2 be 2 NFA- be 2 NFA- ’s as follows ’s as follows q1,0 q1,f M1 q2,0 q2,f M2 M1 = (Q1, , , q1,0, F1) M2 = (Q2, , , q2,0, F2)
  • 44.
            44  -Transitions (7) -Transitions(7)  L(M) = L(M L(M) = L(M1 1) )   L(M L(M2 2) ) q1,0 q1,f M1 q2,0 q2,f M2 q0   M = (Q1  Q2  {q0}, , , q0, F1  F2) is the same as in 1 and 2, but add: (q0, ) = {q1,0, q2,0}
  • 45.
            45  -Transitions (8) -Transitions(8)  L(M) = L(M L(M) = L(M1 1)L(M )L(M2 2) ) q1,0 q1,f M1 q2,0 q2,f M2  M = (Q1  Q2, , , q1,0, F2) is the same as in 1 and 2, but add: (q, ) = {q2,0}, where q  F1
  • 46.
            46  -Transitions (9) -Transitions(9)  L(M) = L(M L(M) = L(M1 1) )* * q1,0 q1,f M1  qf q0    M = (Q1  {q0, qf}, , , q0, {qf}) is the same as in 1, but add: (q0, ) = {q1,0 ,qf} (q1,f, ) = {q1,0 ,qf}, where q1,f F1
  • 47.
            47  -Transitions (10) -Transitions(10) Given the regular expression : a(b* c) | a( b | c+ | ) Find a transition diagram NFA-  that recognizes it.
  • 48.
            48  -Transitions (11) -Transitions(11) 3 2 b c a 1 6 5 7 c a c 4 b a (b* c) a( b | c+ | ) Now that you have the individual diagrams, “or” them as follows:
  • 49.
  • 50.
            50  -Transitions (12) -Transitions(12)  See examples 2.7, 2.8, 2.9, and 2.10 See examples 2.7, 2.8, 2.9, and 2.10
  • 51.
            51 2.3: Equivalenceof DFA & NFA (1) 2.3: Equivalence of DFA & NFA (1)  Is NFA more powerful than DFA? NO! Is NFA more powerful than DFA? NO!  NFA inefficient to implement directly, so convert to a DFA that recognizes the same strings  Is there a language accepted by an NFA that is not Is there a language accepted by an NFA that is not accepted by any DFA? No accepted by any DFA? No  NFA is equivalent to DFA. NFA is equivalent to DFA.  Each state in DFA corresponds to a SET of states of the NFA
  • 52.
            52 Removing Nondeterminism(2) Removing Nondeterminism (2)   -closure -closure  In an NFA- In an NFA- , the , the  -closure( -closure(q q) ) of a state of a state q q is the set is the set of all states that can be reached from of all states that can be reached from q q by by following a path whose edges are all labeled by following a path whose edges are all labeled by  . . q0 q1 q2 q3 b    a  b Start -closure(q0) = {q0, q1, q2, q3}  - -closure(q1) = {q1,q3}  - -closure(q2) = {q1,q2,q3}
  • 53.
            53 Removing Nondeterminism(3) Removing Nondeterminism (3) NFA- N = (Q, , , q0, F) -closure(q) : q  Q : set of NFA- states that are reachable from q on -transitions only -closure(T) : T  Q : NFA- states reachable from some state t  T on -transitions only move(T, a) : T  Q, a   : set of states to which there is a transition on input a from some state t  T move({q1, q2, …, qi}, a) = (q1, a)  (q2, a)  …  (qi, a) These 3 operations are utilized by algorithms / techniques to facilitate the conversion process No input is consumed
  • 54.
            54 Removing Nondeterminism(4) Removing Nondeterminism (4)  -closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0 on -moves)  -closure(0, 6) = -closure(0)  -closure(6) = {0, 1, 2, 4, 7}  {6, 1, 2, 4,7} = {0, 1, 2, 4, 6, 7}  move({0, 1, 2, 4, 7}, a) = {3, 8} (since move(2, a)=3 and move(7, a)=8) 0 1 2 3 5 4 6 7 8 9 10         a a b b b start
  • 55.
            55 NFA- NFA-   DFA DFAwith Subset Construction with Subset Construction NFA- N  DFA M construction: Given N = (Q, , , q0, F), define M = (Q’, , ’, q’0, F’) Q’  P(Q), all the possible NFA- states M could be in. q’0 = -closure(q0) F’ = {q’  Q’ | q’  F  } ’(q’, a) = -closure(move(q’, a))  DFA M has a state ERR DFA M has a state ERR   Q’ = P(Q) Q’ = P(Q)  serves as the “error” state, when needed  ’(ERR, a) = ERR, a   By definition of ’
  • 56.
            56 Subset Construction SubsetConstruction Algorithm Concepts Algorithm Concepts First we calculate: -closure(0) (i.e., state 0) -closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0 on -moves) Let A = {0, 1, 2, 4, 7} be a state of new DFA M Start with NFA-: (a | b)*abb 0 1 2 3 5 4 6 7 8 9 10         a a b b b start
  • 57.
            57 Conversion Example(1) Conversion Example (1) b : -closure(move(A,b)) = -closure(move({0,1,2,4,7}, b)) adds {5} (since move(4, b) = 5) From this we have : -closure({5}) = {1,2,4,5,6,7} (since 5614, 67, and 12 all by -moves) Let C = {1,2,4,5,6,7} be a new state in D. Define M(A, b) = C 2nd , we calculate : a : -closure(move(A, a)) and b : -closure(move(A, b)) a : -closure(move(A, a)) = -closure(move({0,1,2,4,7}, a))} adds {3, 8} (since move(2, a) = 3 and move(7, a) = 8) From this we have : -closure({3, 8}) = {1,2,3,4,6,7,8} (since 3614, 67, and 12 all by -moves) Let B = {1,2,3,4,6,7,8} be a new state in D. Define M(A, a) = B
  • 58.
            58 Conversion Example(2) Conversion Example (2) 3rd , we calculate for state B on {a, b} a : -closure(move(B, a)) = -closure(move({1,2,3,4,6,7,8}, a))} = {1,2,3,4,6,7,8} = B Define M(B, a) = B b : -closure(move(B, b)) = -closure(move({1,2,3,4,6,7,8}, b))} = {1,2,4,5,6,7,9} = D Define M(B, b) = D 4th , we calculate for state C on {a, b} a : -closure(move(C, a)) = -closure(move({1,2,4,5,6,7}, a))} = {1,2,3,4,6,7,8} = B Define M(C, a) = B b : -closure(move(C, b)) = -closure(move({1,2,4,5,6,7}, b))} = {1,2,4,5,6,7} = C Define M(C, b) = C
  • 59.
            59 Conversion Example(3) Conversion Example (3) 5th , we calculate for state D on {a, b} a : -closure(move(D, a)) = -closure(move({1,2,4,5,6,7,9}, a))} = {1,2,3,4,6,7,8} = B Define M(D, a) = B b : -closure(move(D, b)) = -closure(move({1,2,4,5,6,7,9}, b))} = {1,2,4,5,6,7,10} = E Define M(D, b) = E Finally, we calculate for state E on {a, b} a : -closure(move(E, a)) = -closure(move({1,2,4,5,6,7,10}, a))} = {1,2,3,4,6,7,8} = B Define M(E, a) = B b : -closure(move(E, b)) = -closure(move({1,2,4,5,6,7,10}, b))} = {1,2,4,5,6,7} = C Define M(E, b) = C
  • 60.
            60 Conversion Example(4) Conversion Example (4) State Input Symbol a b A B C B B D C B C E B C D B E … A …b C …a B … abD … abbE start b b b b b a a a a This gives the transition table for the DFA M of: a
  • 61.
            61 Converting NFA- ConvertingNFA-  to DFA – 2 to DFA – 2nd nd Example Example 0 8 5 4 7 3 6 2 1               b a c   RE: c*(ab)*c* 1st we calculate: -closure(0) -closure(0) = {0, 1, 2, 6, 8} (all states reachable from 0 on -moves) Let A={0, 1, 2, 6, 8} be a state of new DFA M
  • 62.
            62 Conversion Example(1) Conversion Example (1) b : -closure(move(A,b)) = -closure(move({0,1,2,6,8}, b)) There is NO transition on b for all states 0,1,2,6 and 8 Define M(A, b) = Reject 2nd , we calculate : a : -closure(move(A, a)) and b : -closure(move(A, b)) c : -closure(move(A, c)) a : -closure(move(A, a)) = -closure(move({0,1,2,6,8}, a))} adds {3} (since move(2, a) = 3) From this we have : -closure({3}) = {3} (since 33 by -moves) Let B = {3} be a new state. Define M(A, a) = B c : -closure(move(A, c)) = -closure(move({0,1,2,6,8}, c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1,2,5,6,7,8} (since 758, 7512, and 7516 by -moves) Let C = {1,2,5,6,7,8} be a new state. Define M(A, c) = C
  • 63.
            63 Conversion Example(2) Conversion Example (2) b : -closure(move(B, b)) = -closure(move({3}, b)) adds {4} (since move(3, b) = 4) From this we have : -closure({4}) = {1,2,4,5,6,8} (since 458, 4512, and 4516 by -moves) Let D = {1,2,4,5,6,8} be a new state. Define M(B, b) = D 3rd , we calculate : a : -closure(move(B, a)) and b : -closure(move(B, b)) c : -closure(move(B, c)) a : -closure(move(B, a)) = -cclosure(move({3}, a))} There is NO transition on a for state 3 Define M(B, a) = Reject c : -closure(move(B, c)) = -closure(move({3}, c)) There is NO transition on c for state 3 Define M(B, c) = Reject
  • 64.
            64 Conversion Example(3) Conversion Example (3) b : -closure(move(C, b)) = -closure(move({1,2,5,6,7,8},b)) There is NO transition on b for all states 1,2,5,6, and 7 Define M(C, b) = Reject 4th , we calculate : a : -closure(move(C, a)) and b : -closure(move(C, b)) c : -closure(move(C, c)) a : -cclosure(move(C, a)) = -closure(move({1,2,5,6,7,8},a))} adds {3} (since move(2, a) = 3) -closure({3}) = {3} Define M(C, a) = B c : -closure(move(C, c)) = -closure(move({1,2,5,6,7,8},c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1,2,5,6,7,8} (since 758, 7512, and 7516 by -moves) Define M(C, c) = C
  • 65.
            65 Conversion Example(4) Conversion Example (4) b : -closure(move(D, b)) = -closure(move({1,2,4,5,6,8}, b)) There is NO transition on b for all states 1,2,4,5,6, and 8 Define M(D, b) = Reject 5th , we calculate : a : -closure(move(D, a)) and b : -closure(move(D, b)) c : -closure(move(D, c)) a : -closure(move(D, a)) = -closure(move({1,2,4,5,6,8},a))} adds {3} (since move(2, a) = 3) -closure({3}) = {3} Define M(D, a) = B c : -closure(move(D, c)) = -closure(move({1,2,4,5,6,8},c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1,2,5,6,7,8} (since 758, 7512, and 7516 by -moves) Define M(D, c) = C
  • 66.
            66 The ResultingDFA M The Resulting DFA M Which States are FINAL States ? 1, 2, 5, 6, 7, 8 1, 2, 4, 5, 6, 8 0, 1, 2, 6, 8 3 c b a a a c c D C A B c b a a a c c
  • 67.
            67 NFA- NFA-   DFA: Example DFA: Example strings over {a,b} with next-to-last symbol = a a a/b a/b q2 q1 q0  a b  q0 {q0, q1} {q0}  q1 {q2} {q2}  q2    M = ({q0, q1, q2}, {a,b}, , q0, {q2}) q0 q2 q0 q0 q1 q0 q1 q2 a a a a b b b b Equivalent DFA Equivalent DFA
  • 68.
            68 An Exampleof NFA- An Example of NFA-    DFA DFA Consider a simple NFA: Consider a simple NFA: Construct a corresponding DFA: Construct a corresponding DFA: 0 1 1 Start 0 1 q0 q1 {q0} {q0, q1} {q1} ERR ERR Start 1 0 1 0 1,0 1,0
  • 69.
            69 Examples Examples  Seeexamples 2.11, 2.12, and 2.13 See examples 2.11, 2.12, and 2.13
  • 70.
            70 Class Discussion ClassDiscussion Construct a DFA equivalent to this NFA: Construct a DFA equivalent to this NFA: Start 0,1 q0 q1 0 q2 1 {q0, q1} Start 1 {q0} 0 1 {q0,q2} 0 1 0 0
  • 71.
            71 b a,b,c An NFA a 12 a 0 b,c c start Notice that the state with label {0, 1, 2} is from the set of states given by the nondeterministic transition (0, a) = {0, 1, 2}. Also notice that any state whose label contains an accepting state is defined as an accepting state in the deterministic machine. {0,1,2} {2} a a {1,2} b c b c c Converted DFA 0 start b,c Class Discussion Class Discussion
  • 72.
            72 2.4 Reductionof the Number of States in FA 2.4 Reduction of the Number of States in FA  Self study Self study  but not included in the exams material