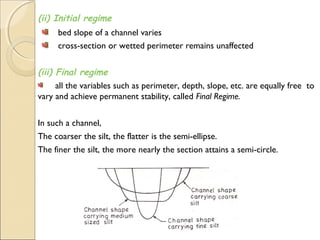
Lacey's regime theory states that the dimensions and slope of a channel are uniquely determined by the discharge, silt load, and erodibility of the soil material. A channel is in regime if there is no scouring or silting. Lacey proposed equations to calculate parameters like velocity, slope, and dimensions based on variables like discharge, silt factor, and side slopes. The theory has limitations as the conditions of true regime cannot be achieved and parameters like silt grade/load are not clearly defined. Lacey also developed shock theory accounting for form resistance due to bed irregularities.

1. Lacey’s Regime TheoryLacey’s Regime Theory
Gerald Lacey -- 1930
Lacey followed Lindley’s hypothesis:
“dimensions and slope of a channel to carry a given discharge and silt load in
easily erodable soil are uniquily determined by nature”.
According to Lacey:
“Silt is kept in suspension by the vertical component of eddies generated at
all points of forces normal to the wetted perimeter”.
Regime Channel
“A channel is said to in regime, if there is neither silting nor scouring”.
According to Lacey there may be three regime conditions:
(i) True regime;
(ii) Initial regime; and
(iii) Final regime.

2. (1)True regime
A channel shall be in 'true regime' if the following conditions are satisfied:
(i) Discharge is constant;
(ii) Flow is uniform;
(iii) Silt charge is constant; i.e. the amount of silt is constant;
(iv) Silt grade is constant; i.e., the type and size of silt is always the same; and
(v) Channel is flowing through a material which can be scoured as easily as it
can be deposited (such soil is known as incoherent alluvium), and is of the
same grade as is transported.
But in practice, all these conditions can never be satisfied. And, therefore,
artificial channels can never be in 'true regime’; they can either be in initial regime
or final regime.

3. (ii) Initial regime
bed slope of a channel varies
cross-section or wetted perimeter remains unaffected
(iii) Final regime
all the variables such as perimeter, depth, slope, etc. are equally free to
vary and achieve permanent stability, called Final Regime.
In such a channel,
The coarser the silt, the flatter is the semi-ellipse.
The finer the silt, the more nearly the section attains a semi-circle.

4. Lacey’s Equations:Lacey’s Equations:
Fundamental Equations:
Derived Equations:
(Lacey’s Non-regime flow equation)
R
V
ffRV
2
2
5
or
5
2
==
52
140VAf =
2
1
3
2
8.10 SRV =
QP 75.4=
6
1
2
140






=
Qf
V
2
1
2
3
4980R
f
S =
6
1
3
5
3340Q
f
S =
2
1
4
31
SR
N
V
a
=
mminsizeiclegrain/partaverageisD
,76.1where
50
50Df =
The equations for determination of Velocity, Slope,
etc are function of the silt factor, whereas silt factor
is function of sediment size.
For upper Indus basin, f = 0.8 to 1.3
For Sindh plain, f = 0.7 to 0.8

5. The above scour depth will be applicable if river width follows the
relationship
For other values of active river width,
where
q = discharge intensity, and
L = actual river width at the given site
31
473.0DepthScourRegimeNormalsLacey' 





=
f
Q
QP 75.4=
L
Q
q
f
q
=





= ,35.1DepthScourNormalsLacey'
31

6. Lacey’s Channel Design ProcedureLacey’s Channel Design Procedure

7. Problem:
Design an irrigation channel in alluvial soil from following data using Lacey’s
theory:
Discharge = 15.0 cumec; Lacey’s silt factor = 1.0; Side slope = ½ : 1
Solution:
sec/689.0)
140
115
()
140
( 6
1
6
1
2
m
Qf
V =
×
==
2
77.21
689.0
15
m
V
Q
A ===
m18.41575.475.4 === QP
m36.1
742.3
)77.21(944.6)4.18(4.18
742.3
944.6 22
=
−−
=
−−
=
APP
D
m36.15)36.1(54.185 =−=−= DPB
m185.1
1
)689.0(
2
5
2
5 22
===
f
V
R
5245
1
)15(3340
)1(
3340 6
1
35
6
1
3
5
=
×
==
Q
f
S

8. Problem:
The slope of an irrigation channel is 0.2 per thousand. Lacey’s silt factor =
1.0, channel side slope = ½ : 1. Find the full supply discharge and dimensions
of the channel.
Data:
S = 0.2/1000 = (0.2 x 5) / (1000 x 5) = 1/5000
Solution:
cumec
S
f
Q
Q
f
S 25.11
5000
13340
1
33403340
6
3
5
6
1
3
5
=








×
=








=⇒=
m
S
f
R
R
f
S 008.1
5000
14980
1
)
4980
(
4980
2
2
2
3
2
1
2
3








×
==⇒=
mQP 93.1525.1175.475.4 ===
2
06.16008.193.15 mPRA =×==
m153.1
742.3
)06.16(944.6)93.15(93.15
742.3
944.6 22
=
−−
=
−−
=
APP
D
m35.13)153.1(593.155 =−=−= DPB

9. Problem:
Design an earthen channel of 10 cumec capacity. The value of Lacey’s silt
factor in the neighboring canal system is 0.9. General grade of the country is
1 in 8000.
Data:
Q = 10 cumec; f = 0.9; Sn=1/8000; B = ?; D = ?; Sreq= ?.
Solution:
Which is steeper than the natural grade of the country (i.e. 1 in 8000),
therefore not feasible.
( ) m/sec622.0
140
9.010
140
6
1
26
1
2
=





=





=
Qf
V
2
m08.16
622.0
10
===
V
Q
A
m02.151075.475.4 === QP
m25.1
742.3
)08.16(944.6)02.15(02.15
742.3
944.6 22
=
−−
=
−−
=
APP
D
m22.12)25.1(502.155 =−=−= DPB
( )
( ) 5844
1
103340
9.0
3340 6
1
3
5
6
1
3
5
===
Q
f
Sreq

10. Now putting S = 1/8000 in the relationship
Hence silt factor will be reduced to 0.7454 by not allowing coarser silt to enter the
canal system by providing silt ejectors and silt excluders.
i.e. silt having mean diameter > 0.179 mm will not be allowed to enter the canal
system.
( )( ) 7454.010
8000
133403340
3340
5
3
6
15
3
6
1
6
1
3
5
=××=



=⇒= SQf
Q
f
S
mm179.0
76.1
76.1
2
5050 =



=⇒= fDDf

11. Lacey's Shock TheoryLacey's Shock Theory
Lacey considered absolute rugosity coefficient Na as;
Constant and
Independent of channel dimensions.
In practice Na varies because;
V-S and y-f relationships are logarithmic,
Due to irregularities or mounds in the sides and bed of the
channel (ripples), pressure on front is more than the pressure on the
rear.
The resistance to flow due to this difference of pressure on the two sides of the
mound is called form resistance.
Lacey termed this loss as shock loss, which is different from frictional resistance
or tangential drag.
Shock loss = f (size, shape and spacing of bed forms)
Total resistance = frictional resistance + shock loss
(due to bed) (due to irregularities)

12. Lacey suggested:
Na should remain constant
Slope should be splited
to overcome friction and
to meet shock loss
i.e.
where, s = slope required to withstand shock losses.
According to Lacey
Na = 0.025 with shock loss
Na = 0.0225 without shock loss
Therefore, s = 0.19 S
i.e. for a channel in good condition
19 % slope for shock loss
and 81 % slope for friction
( ) 2
1
4
31
sSR
N
V
a
−=
( ) 21432143
0225.0
1
025.0
1
sSRSR −=

13. Drawbacks in Lacey’s theory:Drawbacks in Lacey’s theory:
 The concept of true regime is only theoretical and cannot be
achieved practically.
 The various equations are derived by considering the silt
factor of which is not at all constant.
 The concentration of silt is not taken into account.
 The silt grade and silt charge are not clearly defined.
 The equations are empirical and based on the available data
from a particular type of channel.
 The characteristics of regime of channel may not be same for
all cases.

14. Kennedy theory Lacey’s theory
1.It states that the silt carried by the flowing
water is kept in suspension by the vertical
component of eddies which are generated
from the bed of the channel.
1.It states that the silt carried by the flowing
water is kept in suspension by the vertical
component of eddies which are generated
from the entire wetted perimeter of the
channel.
2. Relation between ‘V’ & ‘D’. 2. Relation between ‘V’ & ‘R’.
3. Critical velocity ratio ‘m’ is introduced to
make the equation applicable to diff.
channels with diff. silt grades.
3. Silt factor ‘f’ is introduced to make the
equation applicable to diff. channels with
diff. silt grades.
4. Kutter’s equation is used for finding the
mean velocity.
4. This theory gives an equation for finding
the mean velocity.
5. This theory gives no equation for bed
slope.
5. This theory gives an equation for bed
slope.
6.In this theory, the design is based on trial
and error method.
6. This theory does not involve trial and
error method.