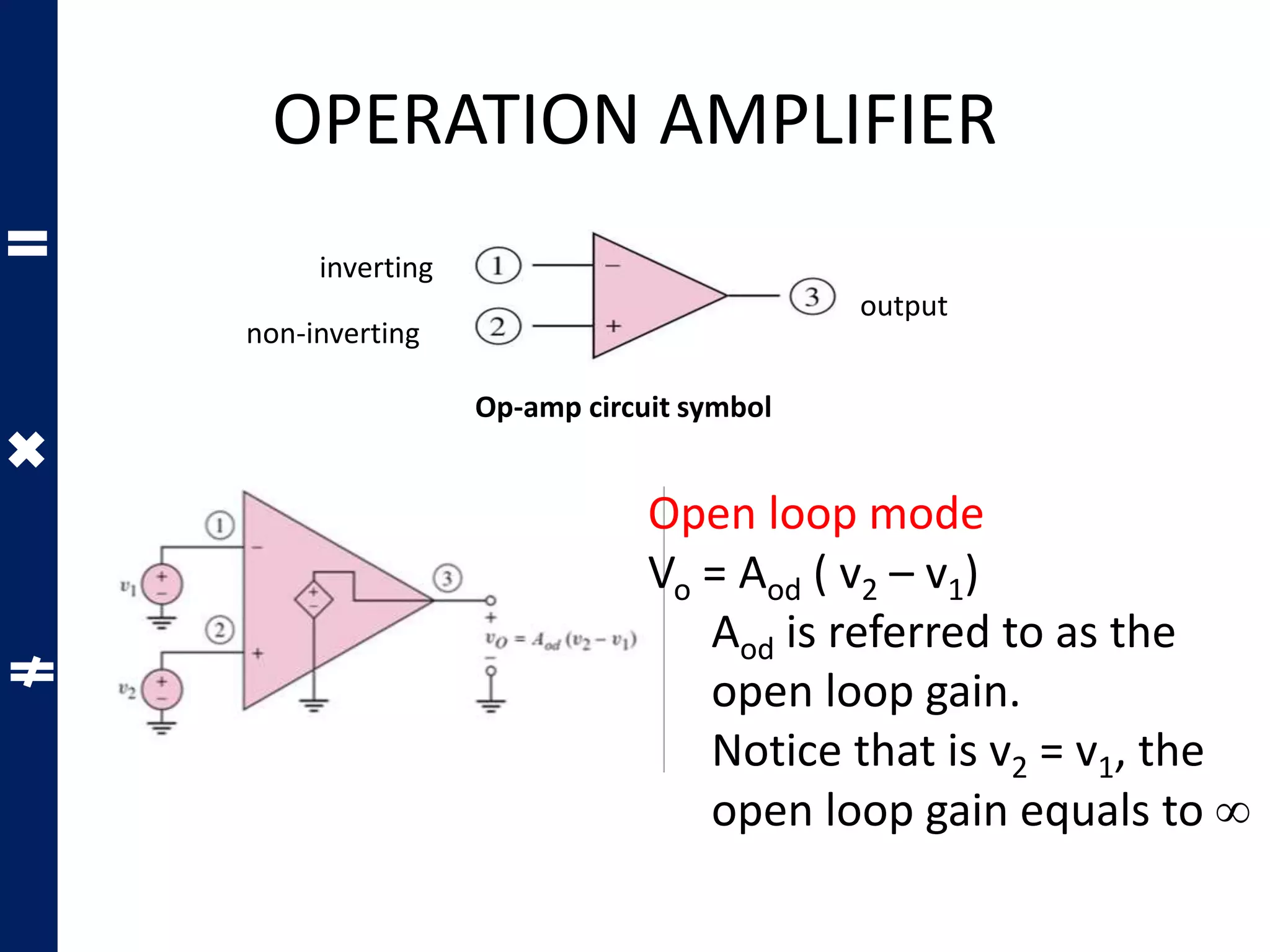
The document discusses operation amplifiers (op-amps) and their uses in different circuit configurations. It describes op-amps being used as:
1) Inverting and non-inverting amplifiers, where the inverting amplifier inverts the input signal and the non-inverting amplifier does not invert it.
2) A summing amplifier, which sums multiple input signals.
3) An integrator, which integrates the input signal over time by using a feedback capacitor instead of resistor.
4) A differentiator, which differentiates the input signal by using an input capacitor instead of resistor.