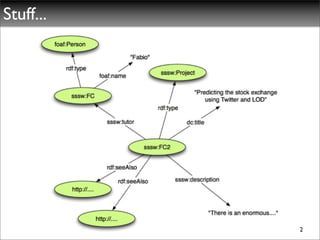
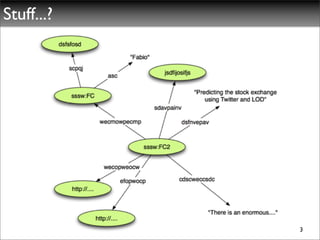
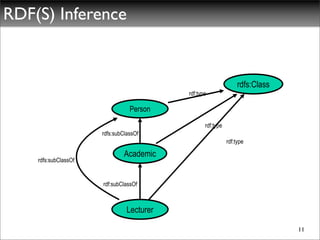
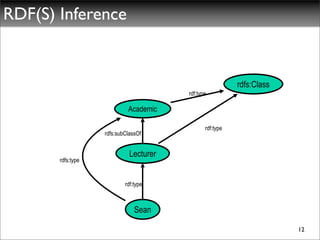
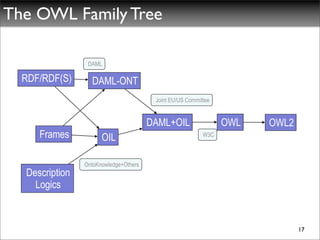
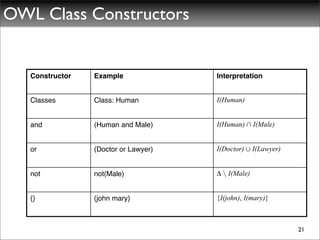
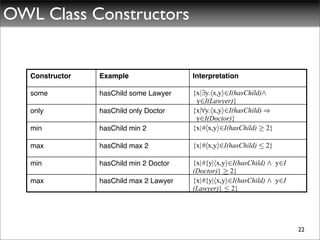
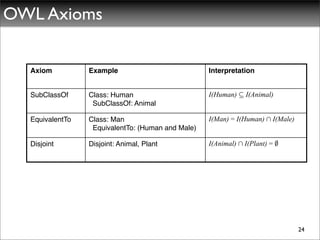
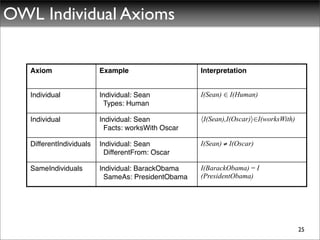
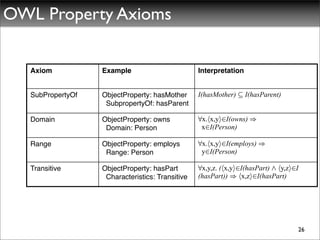
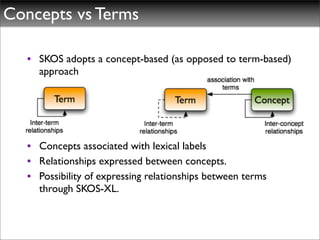
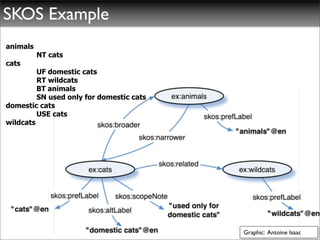
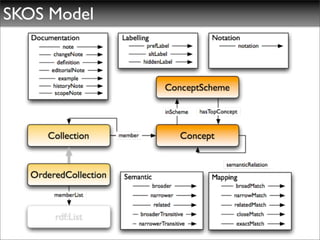
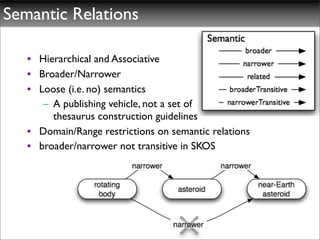
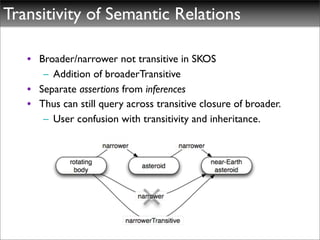
The document discusses ontologies, vocabularies, and semantic web technologies. It provides an overview of RDF, RDF Schema, and OWL, including their semantics and capabilities. It describes how ontologies can constrain models and enable reasoning to derive inferences from class definitions and axioms. The document also addresses some common misconceptions regarding ontology modeling concepts.

1. Ontologies and Vocabularies
Sean Bechhofer
School of Computer Science,
University of Manchester, UK
http://www.cs.manchester.ac.uk
Ontology Languages, SSSW'12

2. Stuff...
2

3. Stuff...?
3

4. Semantic Web
• Metadata
– Describe resources
– No good unless everyone speaks the same
language;
• Terminologies
– provide shared and common vocabularies of a domain,
so search engines, agents, authors and users can
communicate.
– No good unless everyone means the same thing;
• Ontologies
– provide a shared and common understanding of a
domain that can be communicated across people and
applications, and will play a major role in supporting 4

5. Classes/Properties/Individuals
• Many representation languages use an “object oriented
model” with
• Objects/Instances/Individuals
– Elements of the domain of discourse
• Types/Classes/Concepts
– Sets of objects sharing certain characteristics
• Relations/Properties/Roles
– Sets of pairs (tuples) of objects
• Such languages are/can be:
– Well understood
– Formally specified
– (Relatively) easy to use
– Amenable to machine processing 5

6. Structure of an Ontology
Ontologies typically have two distinct components:
• Names for important concepts in the domain
– Elephant is a concept whose members are a kind of
animal
– Herbivore is a concept whose members are exactly
those animals who eat only plants or parts of plants
– AdultElephant is a concept whose members are exactly
those elephants whose age is greater than 20 years
• Background knowledge/constraints on the
domain
– An AdultElephant weighs at least 2,000 kg
– All Elephants are either AfricanElephants or
IndianElephants 6

7. Why Semantics?
• What does an expression in an ontology mean?
• The semantics of a language can tell us precisely how to
interpret a complex expression.
• Well defined semantics are vital if we are to support
machine interpretability
– They remove ambiguities in the interpretation of the
descriptions.
Telephone Black
? 7

8. What does RDF give us?
• A mechanism for publishing data.
• Single (simple) data model.
• Syntactic consistency between names (IRIs).
• Low level integration of data.
– Mash the graphs together and we’re done.
8

9. RDF(S): RDF Schema
• RDF gives a data model and serialisations, but it does not
give any special meaning to schema vocabulary such as
subClassOf or type
– Interpretation is an arbitrary binary relation
• RDF Schema extends RDF with a schema vocabulary that
allows us to define basic vocabulary terms and the
relations between those terms
– Class, Property
– type, subClassOf
– range, domain
9

10. RDF(S)
• These terms are the RDF Schema building blocks
(constructors) used to create vocabularies:
– <Person,type,Class>
– <hasColleague,type,Property>
– <Professor,subClassOf,Person>
– <Carole,type,Professor>
– <hasColleague,range,Person>
– <hasColleague,domain,Person>
• Semantics gives “extra meaning” to particular RDF
predicates and resources
– specifies how terms should be interpreted
– allows us to draw inferences
10

11. RDF(S) Inference
rdfs:Class
rdf:type
Person
rdf:type
rdfs:subClassOf
rdf:type
Academic
rdfs:subClassOf
rdf:subClassOf
Lecturer
11

12. RDF(S) Inference
rdfs:Class
rdf:type
Academic
rdf:type
rdfs:subClassOf
Lecturer
rdfs:type
rdf:type
Sean
12

13. RDF/RDF(S) “Liberality”
• No distinction between classes and instances (individuals)
<Species,type,Class>
<Lion,type,Species>
<Leo,type,Lion>
• No distinction between language constructors and
ontology vocabulary, so constructors can be applied to
themselves/each other
<type,range,Class>
<Property,type,Class>
<type,subPropertyOf,subClassOf>
• In order to cope with this, RDF(S) has a particular non-
standard model theory.
13

14. What does RDF(S) give us?
• Ability to use simple schema/vocabularies when describing
our resources.
• Consistent vocabulary use and sharing.
• Basic inference
14

15. Problems with RDF(S)
• RDF(S) is too weak to describe resources in sufficient
detail
– No localised range and domain constraints
 Can’t say that the range of hasChild is Person when applied to
Persons and Elephant when applied to Elephants
– No existence/cardinality constraints
 Can’t say that all instances of Person have a mother that is also a
Person, or that Persons have exactly 2 parents
– No transitive, inverse or symmetrical
properties
 Can’t say that isPartOf is a transitive property, that hasPart is the
inverse of isPartOf or that touches is symmetrical
15

16. OWL
• OWL: Web Ontology Language
• Extends existing Web standards
– Such as XML, RDF, RDFS
• Is (hopefully) easy to understand and use
– Based on familiar KR idioms
• Of “adequate” expressive power
• Formally specified
– Possible to provide automated reasoning support
16

17. The OWL Family Tree
DAML
RDF/RDF(S) DAML-ONT
Joint EU/US Committee
DAML+OIL OWL OWL2
Frames OIL W3C
OntoKnowledge+Others
Description
Logics
17

18. Aside: Description Logics
• A family of logic based Knowledge Representation
formalisms
– Descendants of semantic networks and KL-ONE
– Describe domain in terms of concepts (classes), roles
(relationships) and individuals
• Distinguished by:
– Formal semantics (typically model theoretic)
 Decidable fragments of FOL
 Closely related to Propositional Modal & Dynamic Logics
– Provision of inference services
 Sound and complete decision procedures for key problems
 Implemented systems (highly optimised)
18

19. OWL (Direct) Semantics
• Model theoretic semantics. An interpretation consists of
– A domain of discourse (a collection of objects)
– Functions mapping
 classes to sets of objects
 properties to sets of pairs of objects
– Rules describe how to interpret the constructors and
tell us when an interpretation is a model.
• Semantics described in terms of
– Individuals in a domain of discourse
– (Binary) Properties that relate individuals
– Classes or collections of individuals
• A class description is a characterisation of the individuals
that are members of that class. 19

20. OWL (Direct) Semantics
• OWL has a number of operators for constructing class
expressions.
• These have an associated semantics which is given in
terms of a domain:
– Δ
• And an interpretation function
– I:concepts ! ℘(Δ)
– I:properties ! ℘(Δ £ Δ)
– I:individuals ! Δ
• I is then extended to concept expressions.
20

21. OWL Class Constructors
Constructor Example Interpretation
Classes Class: Human I(Human)
and (Human and Male) I(Human) Å I(Male)
or (Doctor or Lawyer) I(Doctor) [ I(Lawyer)
not not(Male) Δ I(Male)
{} {john mary} {I(john), I(mary)}
21

22. OWL Class Constructors
Constructor Example Interpretation
some hasChild some Lawyer {x|9y.hx,yi2I(hasChild)^Æ
y2I(Lawyer)}
only hasChild only Doctor {x|8y.hx,yi2I(hasChild) )
y2I(Doctor)}
min hasChild min 2 {x|#hx,yi2I(hasChild) ¸ 2}
max hasChild max 2 {x|#hx,yi2I(hasChild) · 2}
min hasChild min 2 Doctor {x|#{y|hx,yi2I(hasChild) ^Æ y2I
(Doctor)} ¸ 2}
max hasChild max 2 Lawyer {x|#{y|hx,yi2I(hasChild) ^Æ y2I
(Lawyer)} · 2}
22

23. OWL Axioms
• Axioms allow us to add further statements about arbitrary
concept expressions and properties
– Subclasses, Disjointness, Equivalence, characteristics of
properties etc.
• An interpretation I satisfies an axiom if the interpretation
of the axiom is true.
– Axioms constrain the allowed models
– They provide the additional “assumptions” about the
way in which the domain should be interpreted.
• I satisfies or is a model of an ontology (or knowledge base)
if the interpretation satisfies all the axioms in the
knowledge base.
23

24. OWL Axioms
Axiom Example Interpretation
SubClassOf Class: Human I(Human) µ I(Animal)
SubClassOf: Animal
EquivalentTo Class: Man I(Man) = I(Human) Å I(Male)
EquivalentTo: (Human and Male)
Disjoint Disjoint: Animal, Plant I(Animal) Å I(Plant) = ;
24

25. OWL Individual Axioms
Axiom Example Interpretation
Individual Individual: Sean I(Sean) 2 I(Human)
Types: Human
Individual Individual: Sean hI(Sean),I(Oscar)i2I(worksWith)
Facts: worksWith Oscar
DifferentIndividuals Individual: Sean I(Sean) ≠ I(Oscar)
DifferentFrom: Oscar
SameIndividuals Individual: BarackObama I(BarackObama) = I
SameAs: PresidentObama (PresidentObama)
25

26. OWL Property Axioms
Axiom Example Interpretation
SubPropertyOf ObjectProperty: hasMother I(hasMother) µ I(hasParent)
SubpropertyOf: hasParent
Domain ObjectProperty: owns 8x.hx,yi2I(owns) )
Domain: Person x2I(Person)
Range ObjectProperty: employs 8x.hx,yi2I(employs) )
Range: Person y2I(Person)
Transitive ObjectProperty: hasPart 8x,y,z. (hx,yi2I(hasPart) ^Æ hy,zi2I
Characteristics: Transitive (hasPart)) ) hx,zi2I(hasPart)
26

27. Models
• An OWL Ontology doesn’t define a single model, it is a
set of constraints that define a set of possible models
• No constraints (empty Ontology) means any model is
possible
• More constraints means fewer models
• Too many constraints may mean no possible model
(inconsistent Ontology)
27

28. Consequences
• An ontology (collection of axioms) places constraints on
the models that are allowed.
• Consequences may be derived as a result of those
constraints.
• C subsumes D w.r.t. an ontology O iff for every model
I of O, I(D) µ I(C)
• C is equivalent to D w.r.t. an ontology O iff for every
model I of O, I(C) = I(D)
• C is satisfiable w.r.t. O iff there exists some model I of
O s.t. I(C) ≠ ;
• An ontology O is consistent iff there exists some
model I of O.
28

29. Reasoning
• A reasoner makes use of the information asserted in the
ontology.
• Based on the semantics described, a reasoner can help us
to discover inferences that are a consequence of the
knowledge that we’ve presented that we weren’t aware of
beforehand.
• Is this new knowledge?
– What’s actually in the ontology?
29

30. Reasoning
• Subsumption reasoning
– Allows us to infer when one class is a subclass of
another
– B is a subclass of A if it is necessarily the case that (in all
models), all instances of B must be instances of A.
– This can be either due to an explicit assertion, or
through some inference process based on an intensional
definition.
– Can then build concept hierarchies representing the
taxonomy.
– This is classification of classes.
• Satisfiability reasoning
– Tells us when a concept is unsatisfiable
 i.e. when there is no model in which the interpretation of the
30
class is non-empty.

31. Instance Reasoning
• Instance Retrieval
 What are the instances of a particular class C?
 Need not be a named class
• Instantiation
 What are the classes that x is an instance of?
31

32. Necessary and Sufficient Conditions
• Classes can be described in terms of necessary and
sufficient conditions.
– This differs from some frame-based languages where
we only have necessary conditions.
• Necessary conditions
– Must hold if an object is to be an instance of the
class
• Sufficient conditions
– Those properties an object must have
in order to be recognised as a member
of the class.
– Allows us to perform automated If it looks like a
classification. duck and walks
like a duck, then
it’s a duck! 32

33. Misconceptions: Disjointness
• By default, primitive classes are not disjoint.
• Unless we explicitly say so, the description (Animal and
Vegetable) is not unsatifiable.
• Similarly with individuals. The so-called Unique Name
Assumption (often present in DL languages) does not hold,
and individuals are not considered to be distinct unless
explicitly asserted to be so.
33

34. Misconceptions: Domain and Range
• OWL allows us to specify the domain and range of
properties.
• Note that this is not interpreted as a constraint.
• Rather, the domain and range assertions allow us to make
inferences about individuals.
• Consider the following:
• ObjectProperty: employs
Domain: Company
Range: Person
Individual: IBM
Facts: employs Jim
• If we haven’t said anything else about IBM or Jim, this is
not an error. However, we can now infer that IBM is a
Company and Jim is a Person.
34

35. Misconceptions: And/Or and Quantification
• The logical connectives And and Or often cause confusion
– Tea or Coffee?
– Milk and Sugar?
• Quantification can also be contrary to our intuition.
– Universal quantification over an empty set is true.
– Sean is a member of hasChild only Martian
– Existential quantification may imply the existence of an
individual that we don’t know the name of.
35

36. Misconceptions: Closed and Open Worlds
• The standard semantics of OWL makes an Open World
Assumption (OWA).
– We cannot assume that all information is known about
all the individuals in a domain.
– Facilitates reasoning about the intensional definitions of
classes.
– Sometimes strange side effects
• Closed World Assumption (CWA)
– Named individuals are the only individuals in the
domain
• Negation as failure.
– If we can’t deduce that x is an A, then we know it must
be 36

37. Annotations
• OWL defines annotation properties.
• These allow us to assert information about things
(classes, properties, individuals) that don’t contribute to
the logical knowledge.
– No semantics (in the direct semantics)
• Information not about the domain but about the modelling
or description of the domain
– e.g. DC style creation metadata
• Annotations could also be used to support applications
– e.g. labels (cf SKOS.....)
37

38. Profiles
• OWL Profiles describe subsets of the language that offer
the potential for simpler/more efficient implementation
• OWL EL
– Roughly existential quantification of variables.
• OWL QL
– No class expressions in existential quantifications.
– Query answering via rewrites into standard relational
queries
• OWL RL
– Amenable to implementation using rule-based
technologies.
38

39. Lightweight Vocabularies
• For many applications, lightweight representations are
more appropriate.
• Thesauri, classification schemes, taxonomies and other
controlled vocabularies
– Many of these already exist and are in use in cultural
heritage, library sciences, medicine etc.
– Often have some taxonomic structure, but with a less
precise semantics.
39

40. Concept Schemes
• A concept scheme is a set of concepts, potentially
including statements about relationships between those
concepts
– Broader Terms
– Narrower Terms
– Related Terms
– Synonyms, usage information etc.
• Concept schemes aren’t formal ontologies in the way that
OWL ontologies are formal ontologies
– Concepts are not intended to me interpreted as sets
of things in the same way
40

41. SKOS: Simple Knowledge Organisation
• SKOS provides an RDF vocabulary for the representation
of such schemes.
• Designed with a focus on Retrieval Scenarios
A. Single controlled vocabulary used to index and then
retrieve objects
B. Different controlled vocabularies used to index and
retrieve objects
• Mappings then required between the vocabularies
– Initial use cases/requirements focus on these tasks
• Not worrying about activities like Natural Language
translation
41

42. Knowledge Organisation Systems
Thesaurus: Controlled vocabulary in which concepts are represented by
preferred terms, formally organised so that paradigmatic relationships
between the concepts are made explicit, and the preferred terms are
accompanied by lead-in entries for synonyms or quasi-synonyms.
Thesaurus Related Terms
Taxonomy Hierarchy
Authority File Preferred Terms
Synonym Ring Equivalent Terms
Controlled Vocabulary Collection of Terms
Controlled vocabularies: designed for use in classifying or
indexing documents and for searching them.

43. Concepts vs Terms
• SKOS adopts a concept-based (as opposed to term-based)
approach
• Concepts associated with lexical labels
• Relationships expressed between concepts.
• Possibility of expressing relationships between terms
through SKOS-XL.

44. SKOS Example
animals
NT cats
cats
UF domestic cats
RT wildcats
BT animals
SN used only for domestic cats
domestic cats
USE cats
wildcats
Graphic: Antoine Isaac

45. SKOS Model

46. Labelling
• Lexical Labels associated with
Concepts
– Preferred: one per language
– Alternate: variants,
– Hidden: mis-spellings
• No domains stated, so usage possible on any resource.
• Labels pairwise disjoint.
• Label Extension (SKOS-XL) provides additional support
for descriptions of labels and links between them
– E.g. acronyms, abbreviations

47. Documentation
• A number of documentation properties
• Not intended to be comprehensive
• Extension points

48. Semantic Relations
• Hierarchical and Associative
• Broader/Narrower
• Loose (i.e. no) semantics
– A publishing vehicle, not a set of
thesaurus construction guidelines
• Domain/Range restrictions on semantic relations
• broader/narrower not transitive in SKOS

49. Mapping Relations
• Subproperties of Semantic Relations
• Intended for cross-scheme usage
– Although no formal enforcement

50. SKOS and OWL
• SKOS itself is defined as an OWL ontology.
• A particular SKOS vocabulary is an instantiation of that
ontology/schema
– SKOS Concept is a Class, particular concepts are
instances of that class
• Allows use of OWL mechanisms to define properties of
SKOS (e.g. the querying of the transitive closure of
broader).
–

51. Transitivity of Semantic Relations
• Broader/narrower not transitive in SKOS
– Addition of broaderTransitive
• Separate assertions from inferences
• Thus can still query across transitive closure of broader.
– User confusion with transitivity and inheritance.

52. SKOS and OWL
• SKOS and OWL are intended for different purposes.
– OWL allows the explicit modelling/description of a
domain
 Support for inference, automated classificationm detection of
inconsistencies etc.
– SKOS provides vocabulary and navigational structure
• Interactions between representations
– Presenting OWL ontologies as SKOS vocabularies
– Enriching SKOS vocabularies as OWL ontologies.
– Use of SKOS as annotation vocabulary

53. Hands On
• Explore some example vocabularies in order to
understand the semantics.
• Investigate what the inferences are that we can draw,
based on the class definitions and additional axioms in the
ontologies.
53