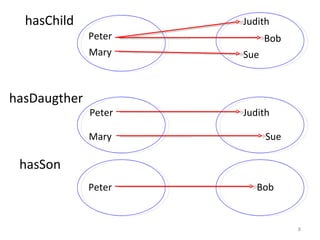
This document discusses ontology representation using RDF/OWL. It covers: 1) OWL is the W3C standard ontology language based on RDF triples. Turtle syntax is commonly used. 2) The basic constructs of OWL like classes, properties, and individuals are introduced. Properties have domains, ranges, and other characteristics. 3) Complex class expressions can be used to define classes as unions, intersections, or negations of other classes. Necessary and sufficient conditions are explained.

1. Ontology representation
Guus Schreiber, VU
Ontology Engineering course

2. RDF/OWL
 Ontology language used in this course
 OWL = W3C Ontology Web Language
 RDF is basis of representation
– Triples = binary relation format
– Turtle is the triple syntax format most frequently
used
2

3. Background reading
OWL Primer, W3C Recommendation, October
2009, http://www.w3.org/TR/owl2-primer/.
 Section 4 contains the basic constructs
 Secs. 5-8 describe the advanced features (not all
of these will be used in the course).
 The Turtle syntax is easiest to read. You can hide
the other in the beginning of the document.
3

4. Some notes about syntax
 Protégé hides most of the syntax details
 OWL has quite a few syntax formats
 If you want to look at OWL syntax we
recommend that you use the Turtle syntax
 Background reading on Turtle):
h
http://wikitravel.org/en/Wikitravel:Turtle_RDF
4

5. Class
 Central grouping construct
 Its instances are called “members”
 Classes can have multiple sub-classes
 Classes can have multiple super-classes
 Root class is conventionally called Thing: the
super-class of all classes
– Nothing is a sub-class of all classes
5

6. Property
 Properties define relationships
 RDF/OWL properties have a direction
Artist creates Artwork
– Compare with UML!
 Two types of properties
– Object property: relationship between two classes
– Datatype property: relationship between a class and a
value space (integers, strings, dates)
 Terminology:
– Subject = left hand of relation
– Object = right hand of relation
6

7. Property hierarchy
 Properties may have sub-properties
hasChild
hasDaugther
hasSon
 Logically sub-properties represent
relationships between subsets of the super-
property
7

8. hasChild Judith
Peter Bob
Mary Sue
hasDaugther
Peter Judith
Mary Sue
hasSon
Peter Bob
8

9. Domain and range
 Artist creates Artwork
 Artist is the domain
– Class of allowed “values” at the left side (origin( of
the relationship
 Artwork is the range
– Class of allowed “values” at the right side
(destination) of the relationship
9

10. Property characteristics (1)
 Functional property
– For each subject this relation has at most one
object
– hasBiologicalMother
 Inverse-functional property
– For each object this relation has are most one
subject
– hasStudentNumber
10

11. Property characteristics (2)
 Symmetric property
– IF i1 p i2 THEN i2 p i1
– Example: friend
 Asymmetric property
– IF i1 p i2 THEN NOT i2 p i1
– Example: parent
11

12. Property characteristics (3)
 Transitive property
– IF i1 p i2 AND i2 p i3 THEN i1 p i3
 Example: partOf
– If Amsterdam is a part of North-Holland and
North-Holland is a part of The Netherlands, then
Amsterdam is a part of the The Netherlands.
12

13. Property characteristics (4)
 Inverse property
– P1 inverseOf p2 implies that
IF i1 p1 i2 THEN i2 p2 i1
– Example: hasPart is the inverse of partOf, so if
Amsterdam is a part of North-Holland, then
North-Holland must have Amsterdam as one of its
parts.
13

14. Property characteristics (5)
 Reflexive property
– FORALL p HOLDS i p i
– Example: for the property knows holds that
everybody knows him/herself
 Irreflexive property
– FORALL p MUST NOT HOLD I p I
– Example: for the parent relation holds that no one
can be his own parent
14

15. Individual
 Instances of classes
– Rembrandt is and individual and member of the
Artist class
 Note: Protégé-OWL supports meta-classes
(classes which members are classes) poorly!
 Enumerated class: a class for which all
individual members can be listed
– Da Ponte opera’s of Mozart: Nozze di Figaro, Cosi
fan tutte, Don Giovanni
15

16. Equality and inequality of individuals
 Equality example: two people (with different
URLs) are actually the same:
ex:Jim sameAs ex:James
 Inequality example: two people are different
Ex1:Jim differentFrom ex2:Jim
 Important on the Web!
– Difference between closed and open world
16

17. Cardinality restrictions of properties
 Defines how many relationships of a certain
type there can be for a particular subject
 Examples:
– Person marriedTo max 1
– Course hasTutor min 1
– Person hasParent exactly 2
17

18. Value restrictions of properties
 Defines to what objects a subject can be related
through a particular relation
 Examples
– Wine producedBy only Vineyard
Wine is only produced by vineyards
– RedWine color value “Red”
Red wines have a red color
– Bicycle hasPart some Wheel
Bicycles consist, amongst others, of at least one wheel
18

19. Equivalent classes & properties:
simple
 States that two classes are the same, for example
two classes in different ontologies
wn-en:Dog = wn-it:Cane
 You can do the same for properties
ex1:hasPart = ex2:hasComponent
 Question: do you think equivalence occurs
frequently?
19

20. Interlude:
the notion of class extension
 OWL is derived from “description logic”
 Description logic takes an “extensional” view of
classes:
– Two classes are the same if - and only if- they have
the same class extension
– The class extension is the set of members of the class
 Question: does this correspond to your intuition?
20

21. Equivalent classes: complex (1)
 A class as the union of other classes
Parent = Mother or Father
 In terms of class extensions:
– The class extension of the class Parent is the union
of the class extensions of the classes Mother and
Father
– OWL calls such formulas “class expressions” (term
used in Protégé)
21

22. Equivalent classes: complex (2)
 A class as the intersection of other classes
Mother =Woman and Parent
 In words: members of the Mother class must
be members of both the Woman and the
Parent class
 You can build even more complex
expressions:
Mother = Woman and some hasChild
22

23. Class expressions
 Statements such as Woman and Parent and
Woman and some hasChild are called class
expressions
 Description logic treats class expressions as
anonymous classes
– i.e. concepts with no symbol, cf. the concept triad
23

24. Equivalent classes: complex (3)
 Defining a class as the negation
(“complement”) of other classes
ChildlessPerson = Person and not Parent
 In words: a childless person is a member of
the person class who does not belong to the
extension of the parent class
24

25. Necessary class definitions
 Description logic is used for classification
reasoning
 A necessary definition state a constraint which
must be true for class membership, but is not
enough to classify it as a member of the class
 Example: red wine must have a red color
– But: not all red things are red wines
25

26. Necessary class definitions in
description logic
 The red-wine constraint is expressed as follows:
– Red wine is subclass of the class of all red things
 More formally: necessary conditions are stated
as a constraint that the class in question (red
wine) is a subclass of the anonymous class
represented by the class expression (class of all
red things)
 This explains how Protégé uses the
“Superclasses”
– Test this now; you’ll get the hang of it
26

27. Sufficient class definitions
 Sufficient definitions allow us to classify an
individual as a member of a class
 Example: if we know someone belongs to the
Woman and Parent class, we also know she
belongs to the Mother class
 The equivalent-class expression represent
sufficient definitions
27

28. Annotations
 Annotations are used to add metadata to
classes and properties
 Annotations play no role in classification
 Example annotations:
– Human-readable label (in multiple languages)
– Time created
– See also Dublin Core elements
28

29. Class exercise: comparison with UML
class diagrams
 Make list of
– Similarities
– Differences
 Don’t forget that OWL is a Web language!
29

30. Guidelines for naming concepts
 Keep original names, where possible
 Prefer more specific names over general ones
 Don’t be afraid of long names if you have to
invent a name
 Use a consistent format
– Here: ClassName propertyName
– But alternatives are fine
30

31. Class room exercise
 “Artefacts are created by humans. Art works
are a kind of artefact. If a person has created
an art work we call him/her an artist.”
 Exercise: create with the help of Protégé an
OWL ontology for this domain description.
31