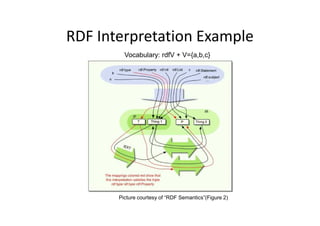
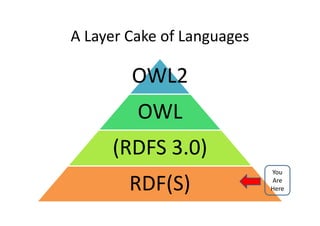
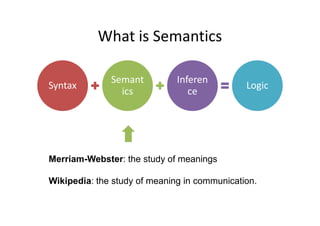
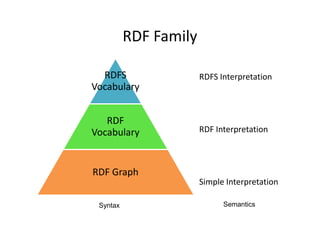
This document provides an overview of RDF semantics. It defines semantics as the study of meaning in communication and models as linking intensional and extensional meaning. It discusses RDF syntax as triples and graphs. It then defines simple interpretation and semantic conditions for RDF graphs. Finally, it defines RDFS vocabulary and semantic conditions for RDFS, including domains, ranges, and subclass/subproperty relationships.

1. RDF Semantics
by Patrick Hayes
W3C Recommendation
http://www.w3.org/TR/rdf-mt/
Presented by Jie Bao
RPI
Sept 4, 2008
Part 1 of RDF/OWL Semantics Tutorial
http://tw.rpi.edu/wiki/index.php/RDF_and_OWL_Semantics

2. A Layer Cake of Languages
OWL2
OWL
(RDFS 3.0)
You
RDF(S) Are
Here

3. Outline
• What is Semantics?
• RDF: Syntax
• RDF Graph and Simple Entailment
• RDF Interpretation
• RDFS Interpretation

4. What is Semantics
Semant Inferen
Syntax Logic
ics ce
Merriam-Webster: the study of meanings
Wikipedia: the study of meaning in communication.

5. What is Semantics?
• Intensional Meaning
– TW Students are Students with affiliation to the
Tetherless World Group
• Extensional Meaning
– TW Students are the set {Jiao, Ankesh, Jesse,…}

6. Model Theory
Used to link intensional
meaning and extensional
meaning
“Model theory assumes that the
language refers to a 'world', and
Alfred Tarski describes the minimal conditions that
1901-1983 a world must satisfy in order to
Picure source: wikipedia
assign an appropriate meaning for
every expression in the language.”
--RDF Semantics

7. Model: an Example
Expression:
TW Students are Students with affiliation to the
Tetherless World Group
A Model:
…

8. A Few Jargons
• An interpretation is a world with each symbol and each
Interpretation expression assigned an extension.
• An model of a logic theory is an interpretation of the
Model theory that satisfies all constraints specified by the theory
• A logic theory is consistent if it has a model.
Consistency
• A symbol or expression x is satisfiable w.r.t. a logic theory
Satisfiability K if there is a model of K with x’s extension not empty.
• A logic theory K entails another logical theory K’ if every
Entailment model of K is a model of K’

9. Outline
• What is Semantics?
• RDF: Syntax
• RDF Graph and Simple Entailment
• RDF Interpretation
• RDFS Interpretation

10. RDF Family
RDFS RDFS Interpretation
Vocabulary
RDF
Vocabulary RDF Interpretation
RDF Graph
Simple Interpretation
Syntax Semantics

11. Not Covered in the Talk
• Blank Node (b-Node)
• Literals (Datatypes)
• Containers
• Collections
• Reification
• Annotation
• Entailment rules (rule inference)

12. RDF: Triple and Graph
• Triple: (subject, property, object)
– UB × U × UBL (Url, Blank node, Literal)
– e.g., (Jim, is-a, Professor)
– e.g., (Jim, has-surname, “Hendler”) – not covered
– e.g.,(Jim, has-pet, _:x) – not covered
is-a
Professor
Jim has-surname “Hendler”
has-pet
• Graph: A set of triples

13. Outline
• What is Semantics?
• RDF: Syntax
• RDF Graph and Simple Entailment
• RDF Interpretation
• RDFS Interpretation

14. Simple Interpretation
A simple interpretation I of a vocabulary V is defined by:
1. A non-empty set IR of resources, called the domain or universe of I.
2. A set IP, called the set of properties of I.
3. A mapping IEXT from IP into the powerset of IR x IR i.e. the set of sets of
pairs <x,y> with x and y in IR .
4. A mapping IS from URI references in V into (IR union IP)
5. A mapping IL from typed literals in V into IR.
6. A distinguished subset LV of IR, called the set of literal values, which
contains all the plain literals in V
We do not consider RDF vocabulary (e.g., rdf:type), yet.

15. Simple Interpretation
V
IS
IP IR
IEXT

16. Simple Interpretation Example
V={a, b, c}
Picture courtesy of “RDF Semantics”(Figure 1)

17. Simple Semantic Conditions
• if E is a URI reference in V then I(E) = IS(E)
• if E is a ground triple s p o. then I(E) = true if s, p and o are in
V, I(p) is in IP and <I(s),I(o)> is in IEXT(I(p)) otherwise I(E)=
false.
• if E is a ground RDF graph then I(E) = false if I(E') = false for
some triple E' in E, otherwise I(E) =true
• if E is a plain literal "aaa" in V then I(E) = aaa
• if E is a plain literal "aaa"@ttt in V then I(E) = <aaa, ttt>
• if E is a typed literal in V then I(E) = IL(E)
• If E is a blank node and A(E) is defined then [I+A](E) = A(E)
• If E is an RDF graph then I(E) = true if [I+A'](E) = true for some
mapping A' from blank(E) to IR, otherwise I(E)= false

18. Note to Simple Interpreation
• IP may not be in IR
• A property (an element in IP) and its extension
(mapping by IEXT) are separated.
– Thus avoids paradox like the barber paradox (A
barber shaves only those men who do not shave themselves.)

19. Outline
• What is Semantics?
• RDF: Syntax
• RDF Graph and Simple Entailment
• RDF Interpretation
• RDFS Interpretation

20. RDF Vocabulary (rdfV)
• rdf:type rdf:Property
• rdf:XMLLiteral rdf:nil rdf:List rdf:Statement
rdf:subject rdf:predicate rdf:object rdf:first
rdf:rest rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2 ...
rdf:value

21. RDF Semantic Conditions
• x is in IP if and only if <x, I(rdf:Property)> is in
IEXT(I(rdf:type))
– Thus, RDF properties (IP) must be resources (IR) in
the universe.
– (rdf:type rdf:type rdf:Property ) is always true
• More conditions for literals

22. RDF Interpretation Example
Vocabulary: rdfV + V={a,b,c}
Picture courtesy of “RDF Semantics”(Figure 2)

23. Outline
• What is Semantics?
• RDF: Syntax
• RDF Graph and Simple Entailment
• RDF Interpretation
• RDFS Interpretation

24. RDFS Vocabulary (rdfsV)
• rdfs:domain rdfs:range rdfs:Resource
• rdfs:Class rdfs:subClassOf rdfs:subPropertyOf
• rdfs:Literal rdfs:Datatype
• rdfs:member rdfs:Container
rdfs:ContainerMembershipProperty
• rdfs:comment rdfs:seeAlso rdfs:isDefinedBy
rdfs:label

25. RDFS Semantic Conditions
On classes
• x is in ICEXT(y) if and only if <x,y> is in IEXT(I(rdf:type))
– IC = ICEXT(I(rdfs:Class))
– IR = ICEXT(I(rdfs:Resource))
– LV = ICEXT(I(rdfs:Literal))
• If x is in IC then <x, I(rdfs:Resource)> is in
IEXT(I(rdfs:subClassOf))
• If <x,y> is in IEXT(I(rdfs:subClassOf)) then x and y are in IC and
ICEXT(x) is a subset of ICEXT(y)
• IEXT(I(rdfs:subClassOf)) is transitive and reflexive on IC

26. RDFS Semantic Conditions
On properties
• If <x,y> is in IEXT(I(rdfs:domain)) and <u,v> is in
IEXT(x) then u is in ICEXT(y)
• If <x,y> is in IEXT(I(rdfs:range)) and <u,v> is in IEXT(x)
then v is in ICEXT(y)
• IEXT(I(rdfs:subPropertyOf)) is transitive and reflexive
on IP
• If <x,y> is in IEXT(I(rdfs:subPropertyOf)) then x and y
are in IP and IEXT(x) is a subset of IEXT(y)
More for container and literals

27. RDFS Axiomatic triples
Domains
• rdf:type rdfs:domain rdfs:Resource .
rdfs:domain rdfs:domain rdf:Property .
rdfs:range rdfs:domain rdf:Property .
rdfs:subPropertyOf rdfs:domain rdf:Property .
rdfs:subClassOf rdfs:domain rdfs:Class .

28. RDFS Axiomatic triples
Ranges
• rdf:type rdfs:range rdfs:Class .
rdfs:domain rdfs:range rdfs:Class .
rdfs:range rdfs:range rdfs:Class .
rdfs:subPropertyOf rdfs:range rdf:Property .
rdfs:subClassOf rdfs:range rdfs:Class .
More for container, reification, literal, and
annotation…

29. RDFS-Valid Triples
• rdfs:Resource rdf:type rdfs:Class .
• rdfs:Class rdf:type rdfs:Class .
• rdf:Property rdf:type rdfs:Class .
• rdfs:domain rdf:type rdf:Property .
rdfs:range rdf:type rdf:Property .
rdfs:subPropertyOf rdf:type rdf:Property .
rdfs:subClassOf rdf:type rdf:Property.

30. Conclusions
• Model Theory gives semantics to RDF(S)
• RDF and RDFS vocabularies pose semantic
constraints on interpretations
– RDF: type, Property
– RDFS: domain, range, Resource, Class, subClassOf
subPropertyOf
• Will see OWL 1 and OWL 2 extensions to
RDF(S) in the future

31. More on RDF Semantics
• Herman J. ter Horst - Completeness, decidability and
complexity of entailment for RDF Schema and a
semantic extension involving the OWL vocabulary. In
J. Web Sem. 3(2-3):79-115, 2005.
• Jos de Bruijn, Stijn Heymans - Logical Foundations of
(e)RDF(S): Complexity and Reasoning. In ISWC/ASWC
pp. 86-99, 2007.
• Jeff Z. Pan, Ian Horrocks - RDFS(FA) and RDF MT: Two
Semantics for RDFS. In International Semantic Web
Conference pp. 30-46, 2003.