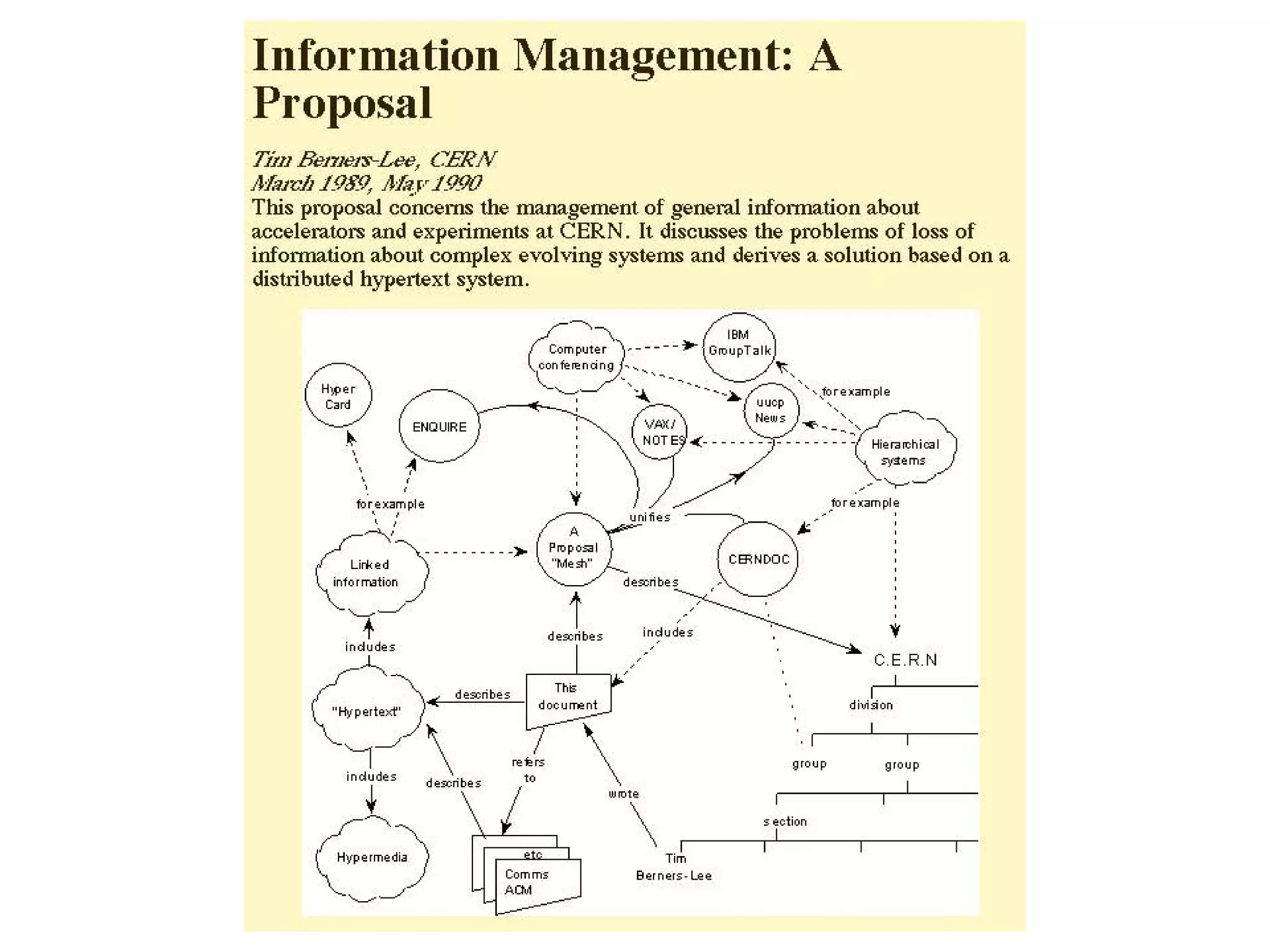
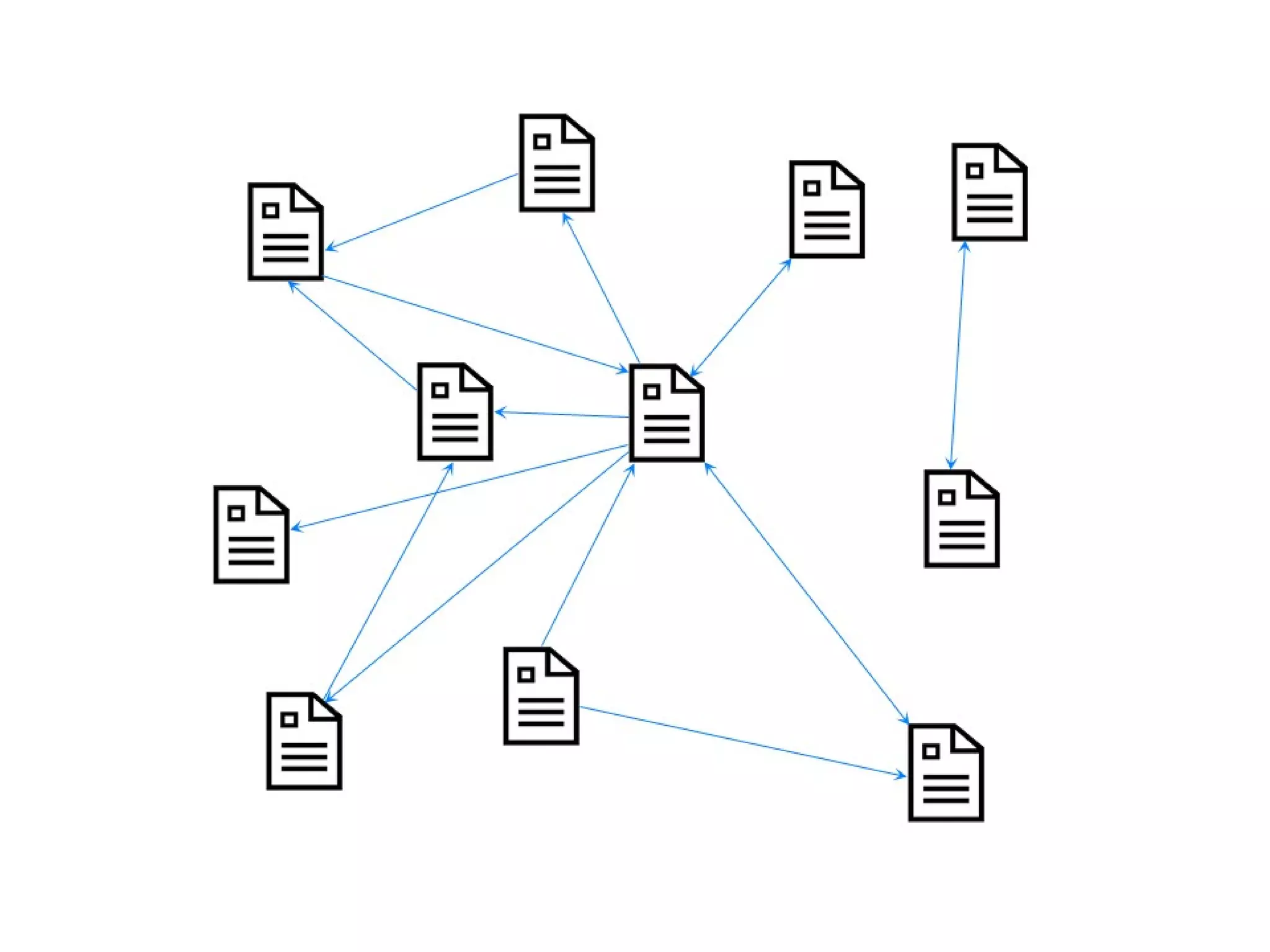
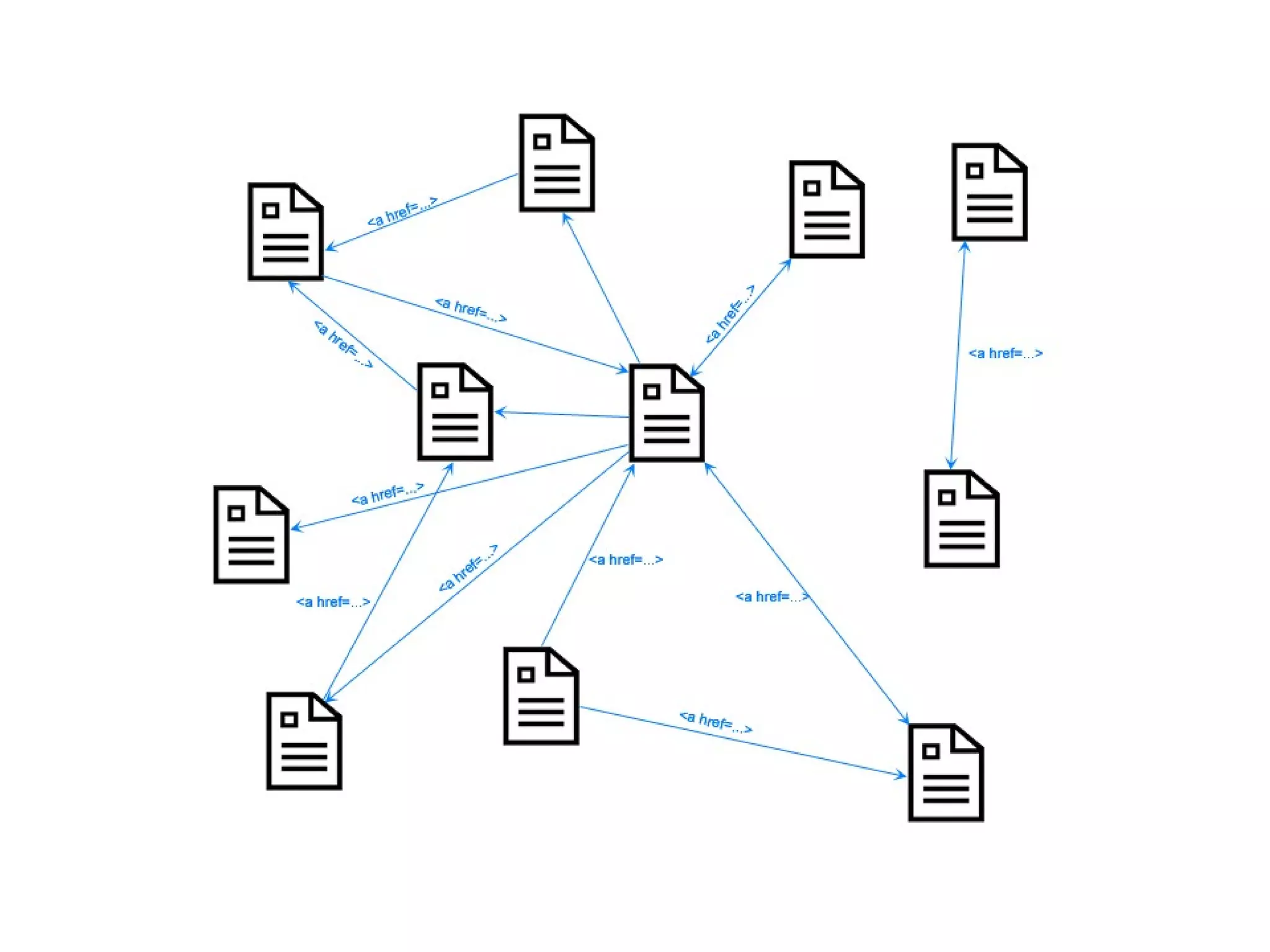
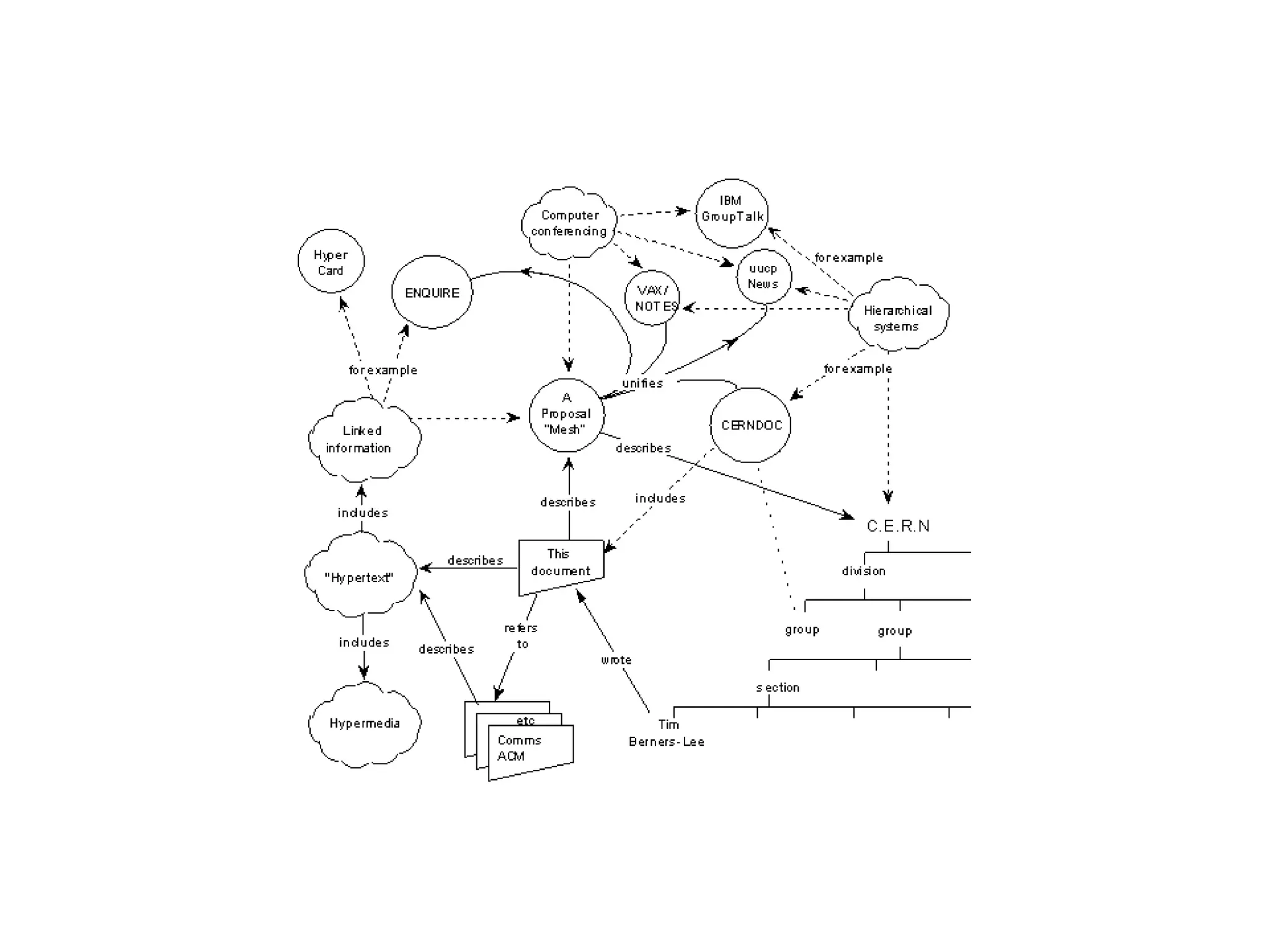
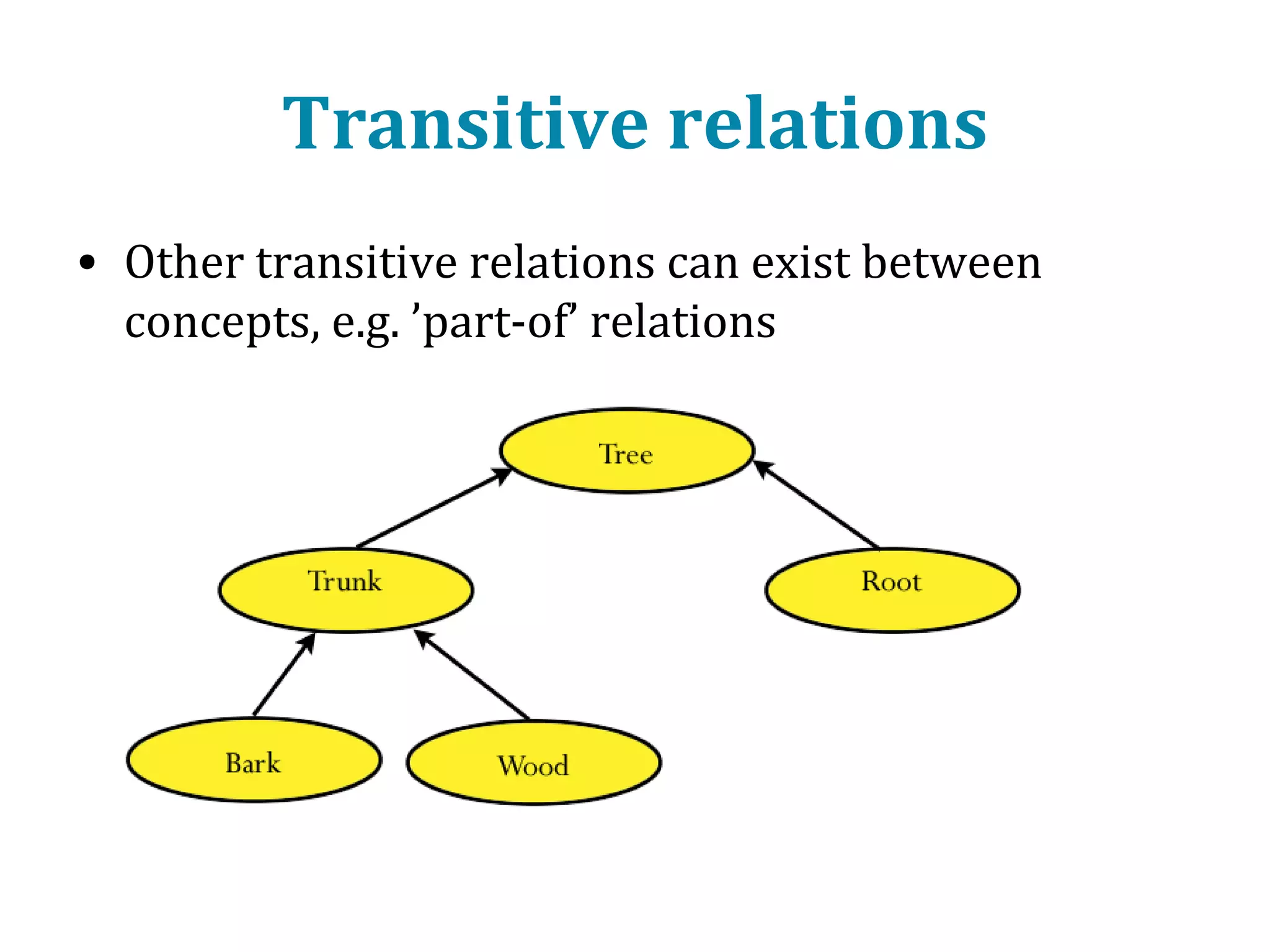
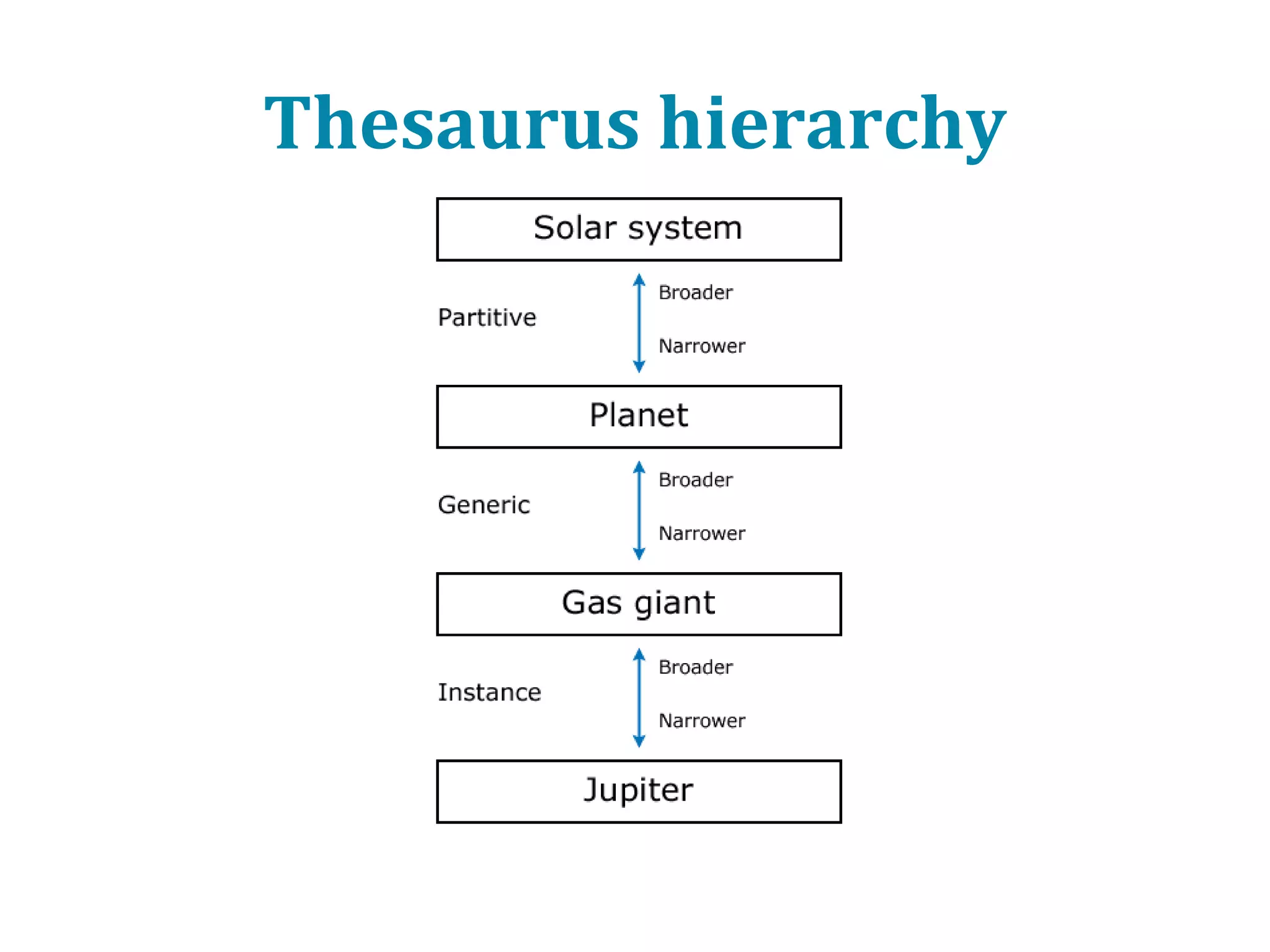
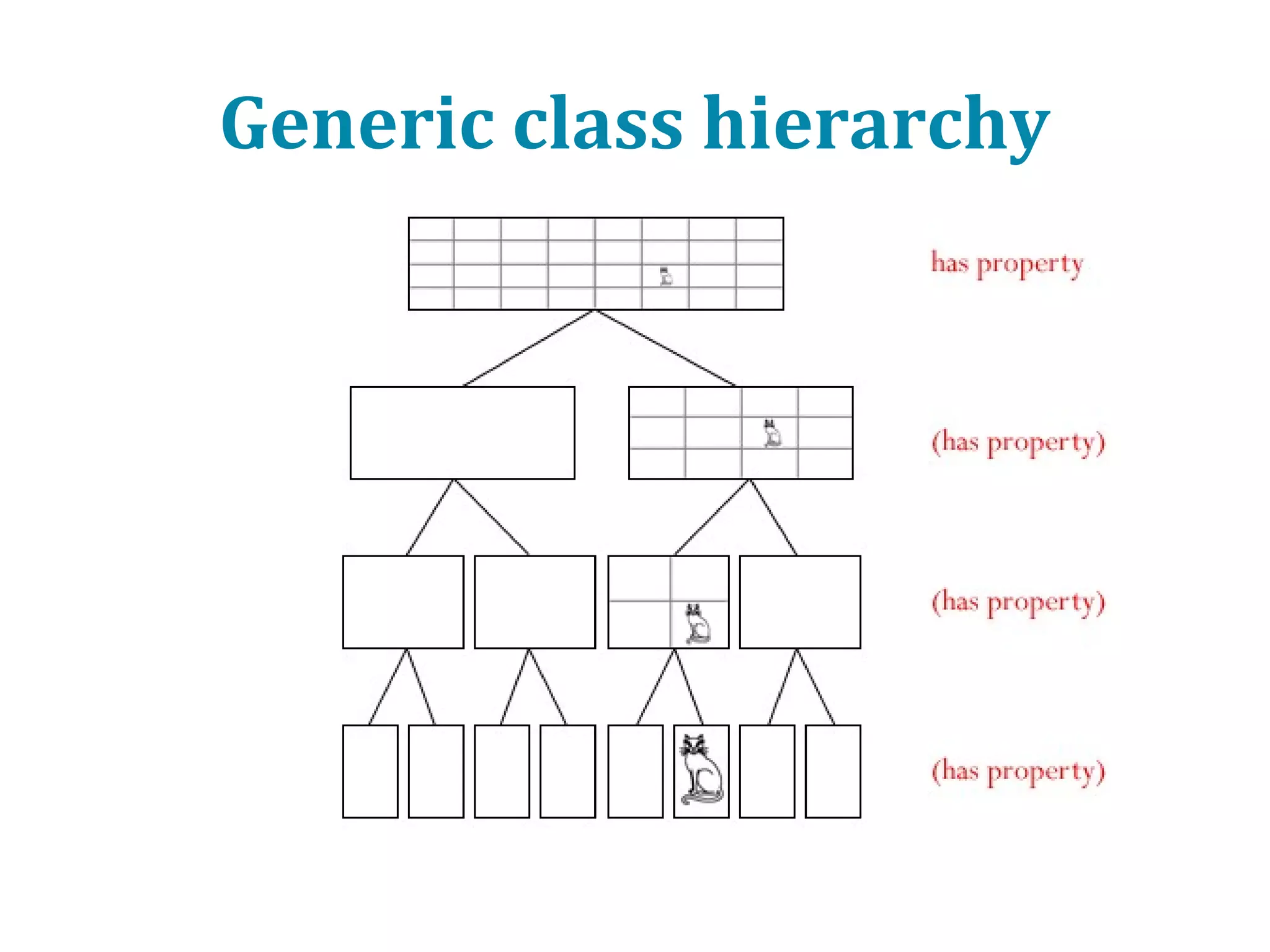
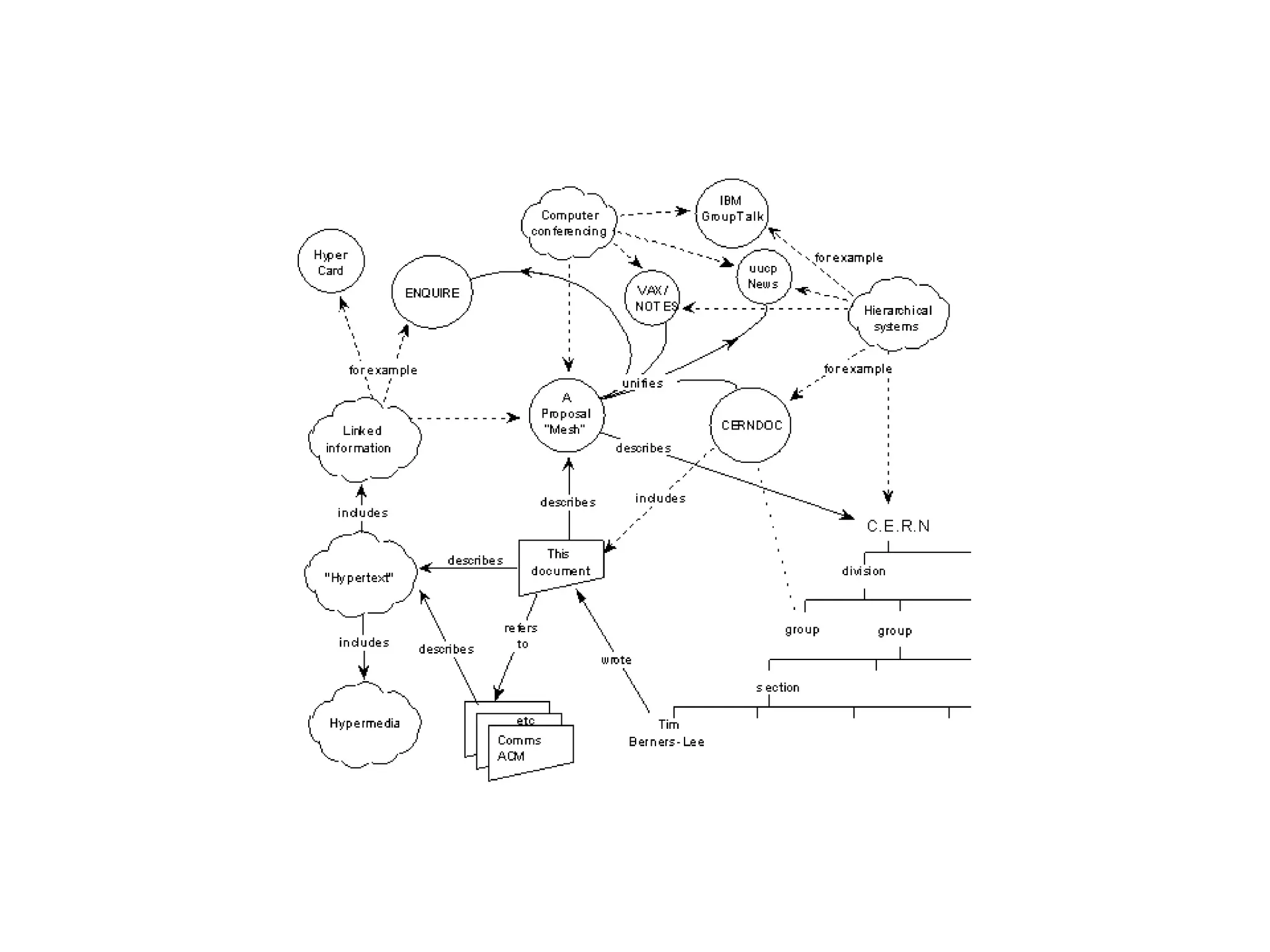
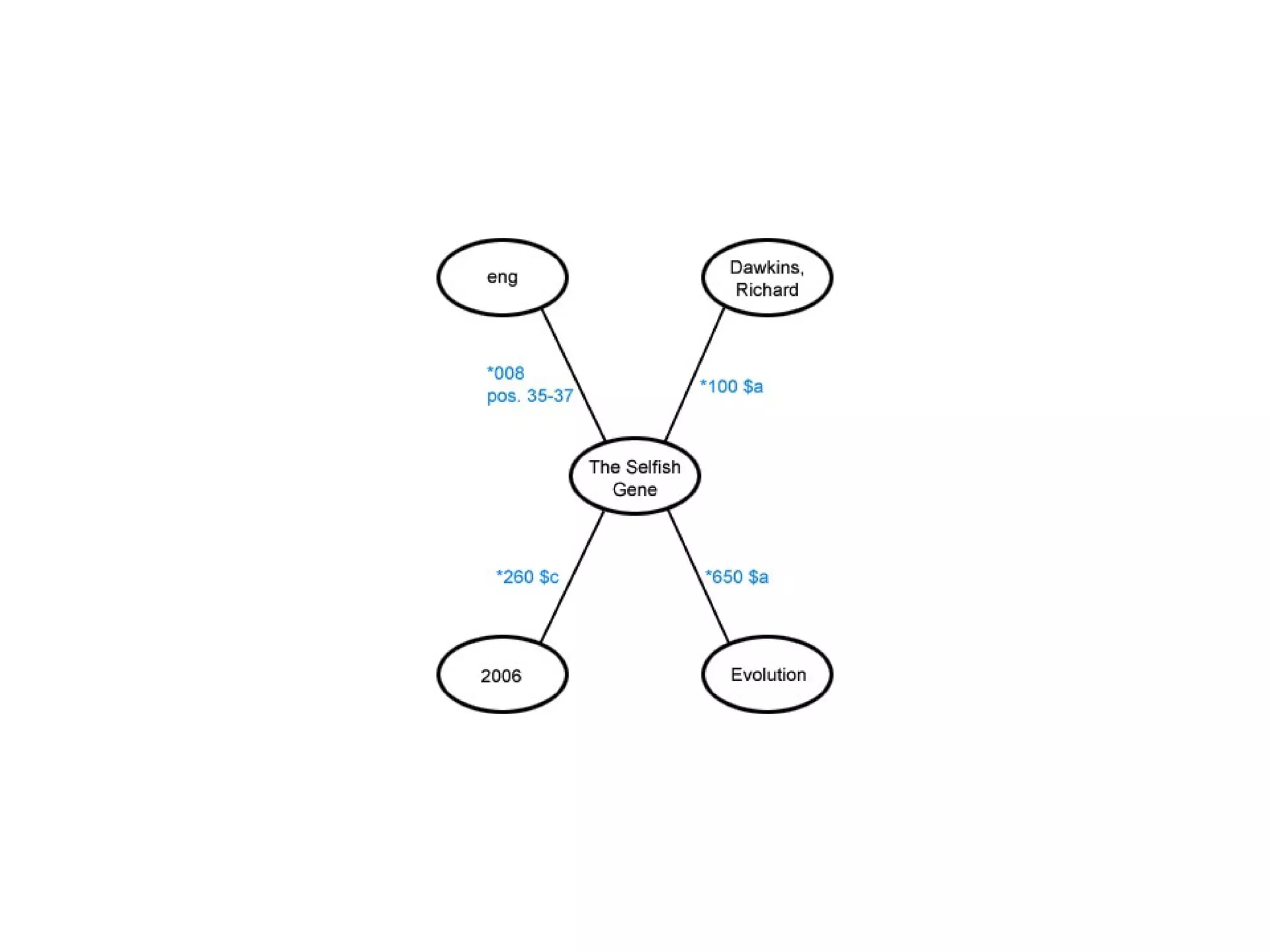
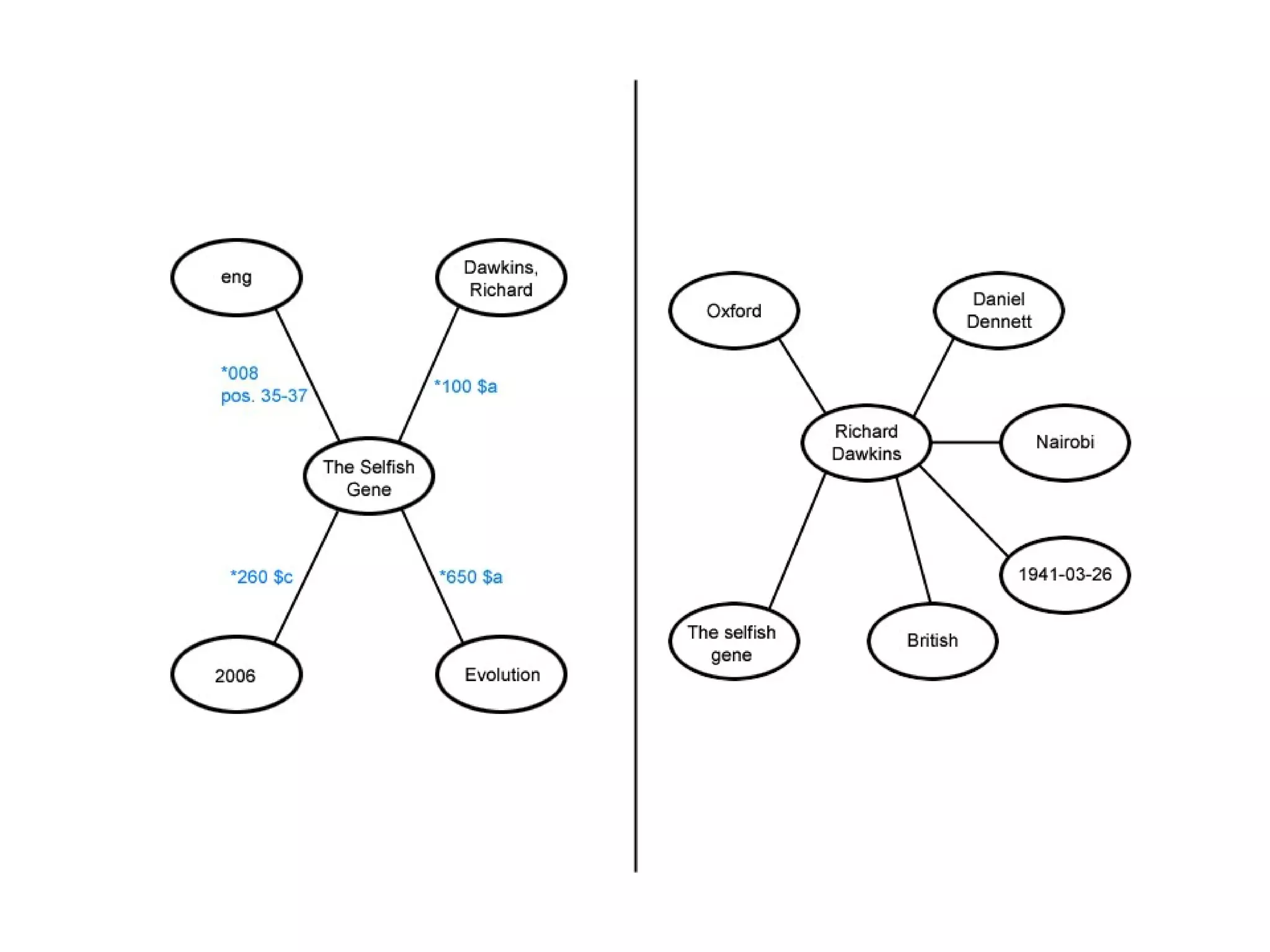
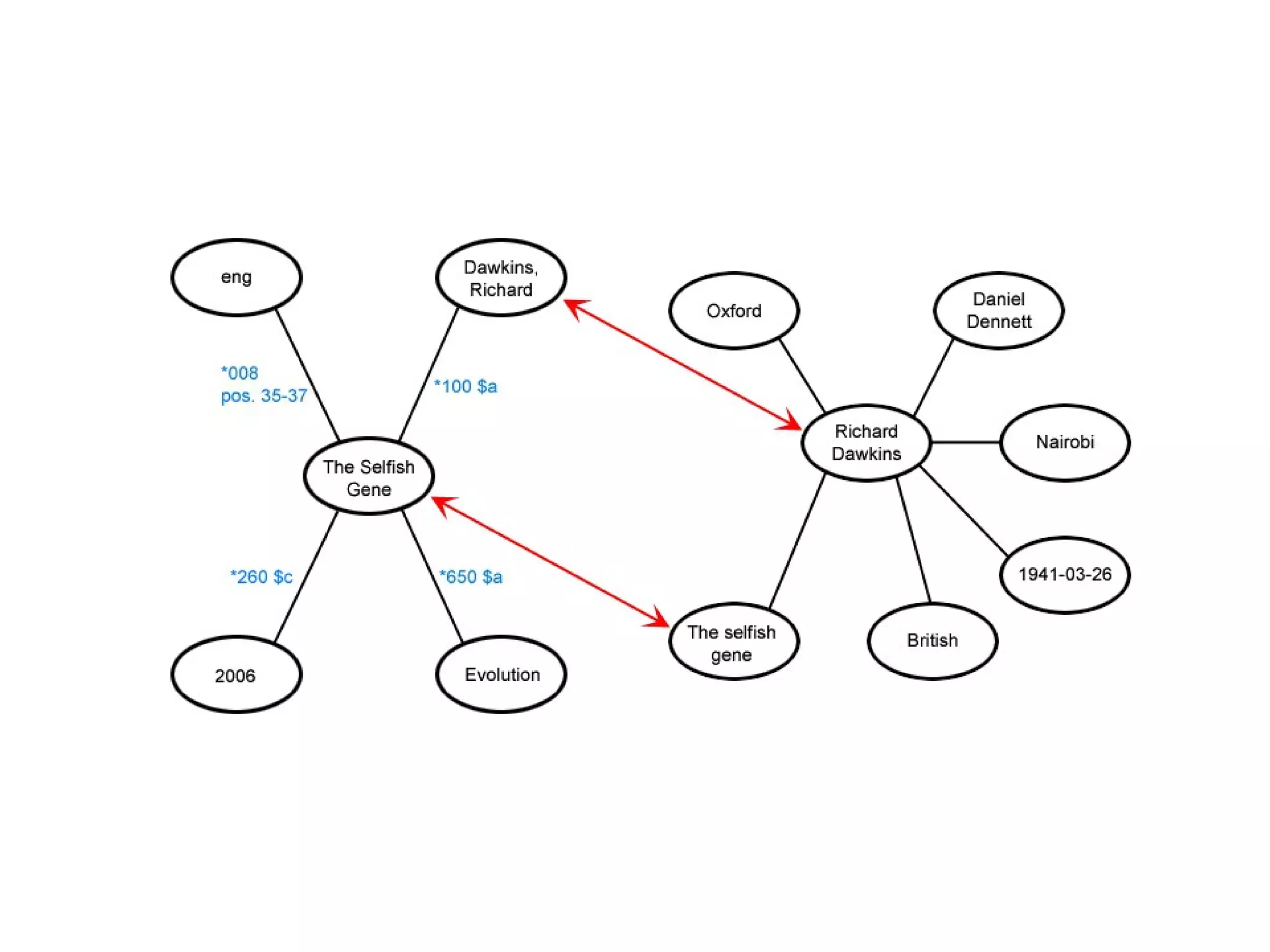
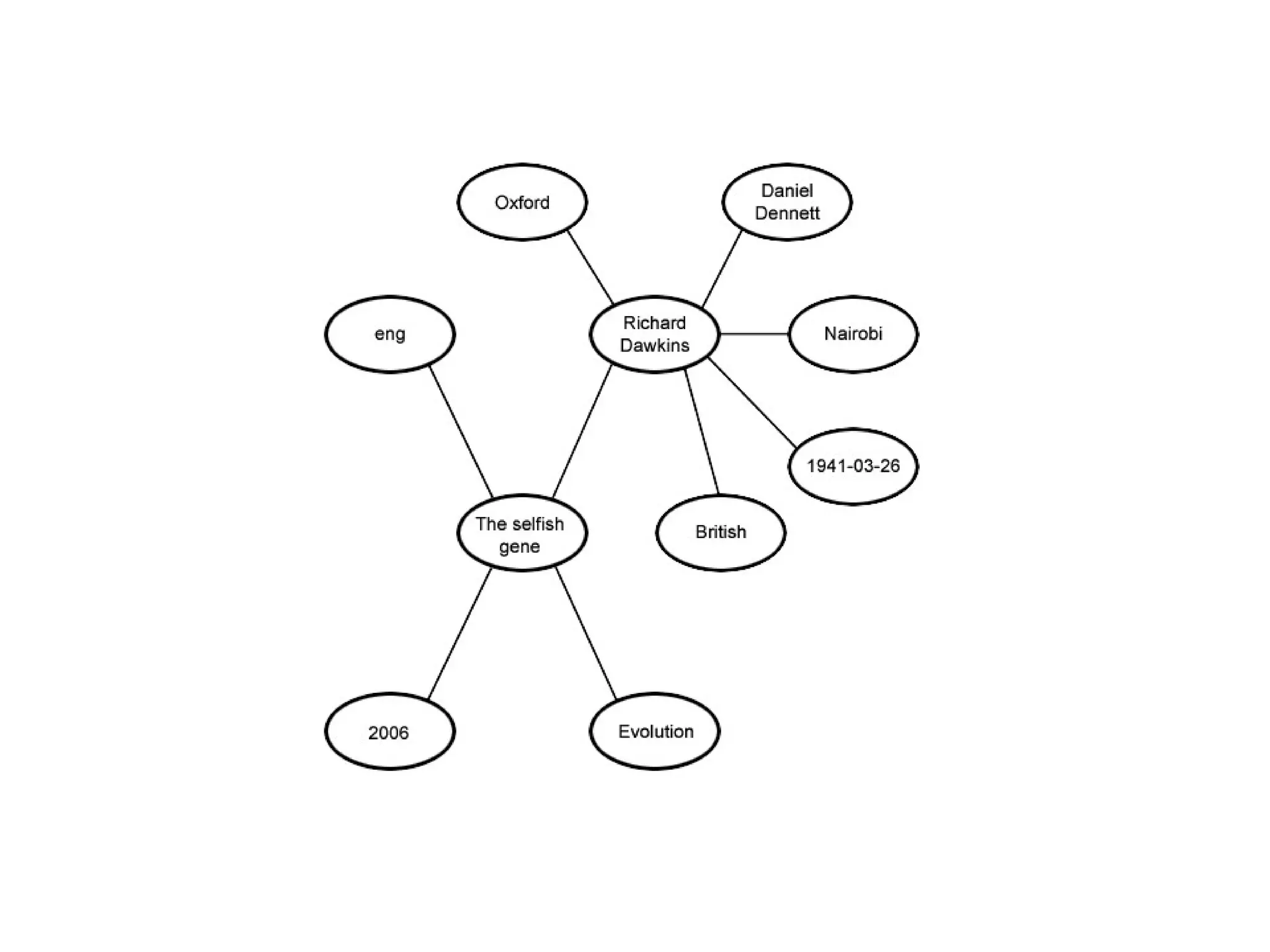
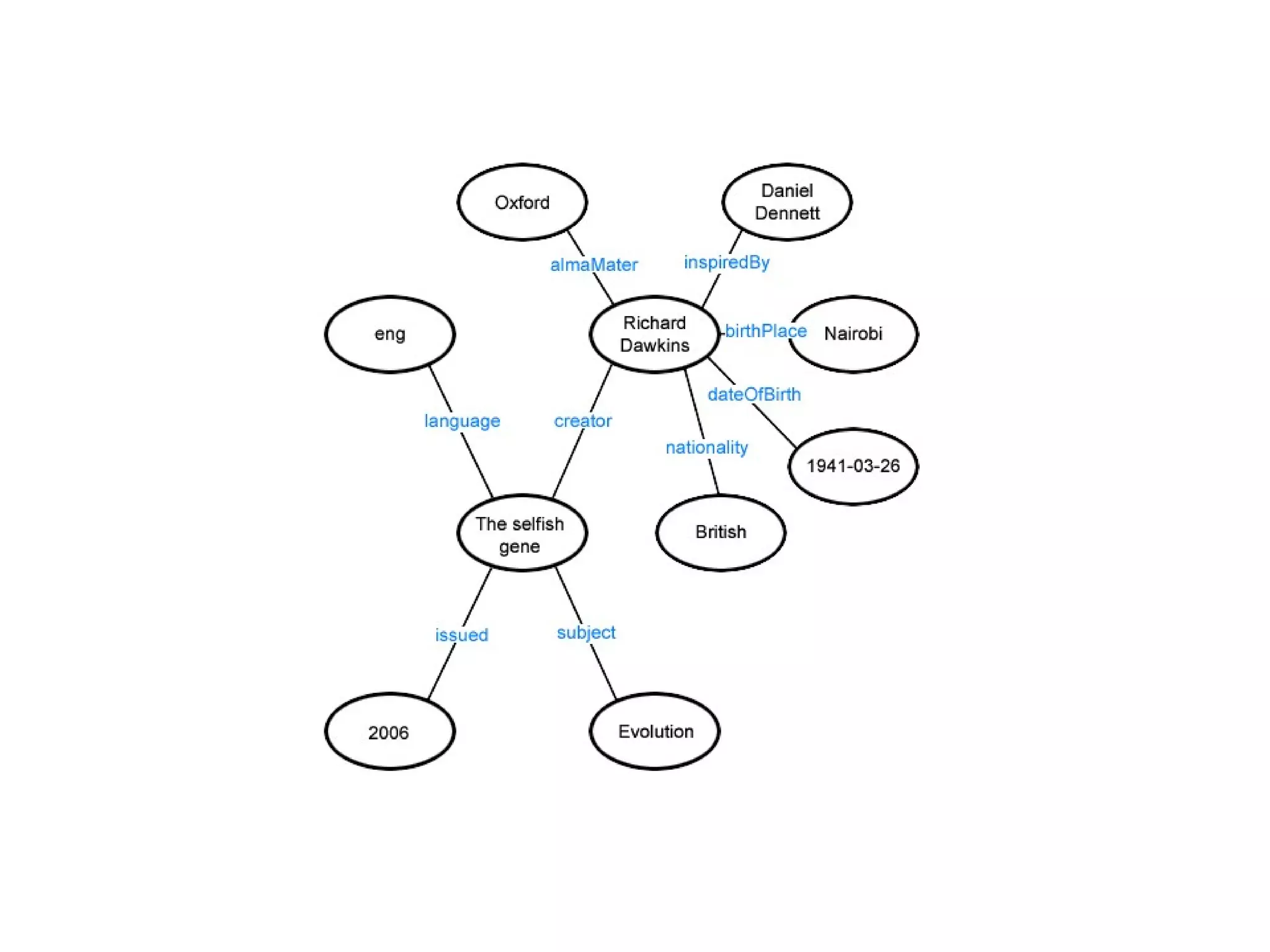
This document provides an introduction to ontology modeling and the semantic web. It defines key concepts such as semantics, ontology, taxonomy, classes, properties, and restrictions. It explains how ontologies can formally represent knowledge through semantic triples that connect instances, classes, and properties. Examples are provided to demonstrate how to construct a simple ontology in Protege that defines classes, subclasses, individuals, and object and datatype properties between them. The document also discusses important ontology modeling principles like the open world assumption.

1. Ontology modelling
and the semantic web
Asgeir Rekkavik
Deichmanske bibliotek

2. What does the word
semantic mean?
• Semantics: The branch of linguistics
concerned with meaning.
(Shorter Oxford English dictionary)
• Semantics is the study of meaning.
(Wikipedia 2013-10-16)

3. I love you
I♥ U
Different syntax, same semantics

9. What does ontology mean?
• Ontology: The science or study of being.
(Shorter Oxford English dictionary)
• In computer science and information science,
an ontology formally represents knowledge
as a set of concepts within a domain, and the
relationships between those concepts.
(Wikipedia 2013-10-16)

10. What does ontology mean?
• The world can be described in many different
ways: e.g. language, art etc.
• An ontology describes the world in a way that is
formal, structured and unambiguous.
• Why? Because we want to describe it to
computers.

11. Ann and Becky are sisters
Ann and Becky are mothers

12. Taxonomies

13. Taxonomies
• Hierarchical classification
• Characteristics
•
•
•
•
Generic relations (’is-a’ relations)
Directed graph
Nodes represent categories
Arrows represent broader/narrower relations
• Especially known from biology. Developed
by Carl von Linné.

14. Taxonomies

15. Transitive relations
• If A is related to B and B is related to C,
then A is related to C
• Examples:
• If Ann is younger than Bob and Bob is younger
than Carl, then Ann is younger than Carl
• If a wolf is a mammal and a mammal is an
animal, then a wolf is an animal.

16. Transitive relations
• Other transitive relations can exist between
concepts, e.g. ’part-of’ relations

17. Different types of relations
• Generic (’is-a’, e.g. Cat - Animal)
• Partitive (’part-of’, e.g. Oslo - Norway)
• Instance (e.g. Socrates - Philospher)
• Equivalence (e.g. Dove – Pigeon)
• Associative (’the rest’)

18. Thesaurus
• Concepts are represented by terms
• Certain types of relations between concepts
are formalized:
• Generic, partitive and instance relations are all
formalized as ’broader / narrower’
• Equivalence relations are formalized as ’use% /
use for ’
• Some associative relations are formalized as
’see also:’

19. Thesaurus hierarchy

20. Thesaurus
• Solar systems
NT: Planets
• Planets
BT: Solar systems
NT: Gas giants
• Gas giants
BT: Planets
NT: Jupiter
• Jupiter
BT: Gas giants

21. Protégé
• Free, open source ontology editor
• Developed by Stanford University and the
University of Manchester
• Available from:
http://protege.stanford.edu

22. Ontology – key concepts
• Classes
• Instances (individuals)
• Properties

23. Classes
• Represent categories, sets of individual
instances
• Are related to eachother through parentchild relationships (superclass-subclass)
• Only generic ’is a’-relations are allowed
• Unlike in a taxonomy, multiple inheritence
is allowed.

24. Generic class hierarchy

25. Generic class hierarchy

26. Properties of classes
• Classes can be:
• Disjoint
(if n is a member of A, n is not a member of B)
(e.g. if Robin is a girl, then Robin is not a boy)
• Equivalent
(if n is a member of A, n is also a member of B and
if n is a member of B, n is also a member of A)
(e.g. Firstgraders ≡ Pupils born in 2007)

27. Exercise
Create a taxonomy with these classes:
•
•
•
•
•
•
•
•
•
•
Bicycle
Boat
Bulldog
Car
Cat
Colour
Dog
Dolphin
Flower
Man
•
•
•
•
•
•
•
•
•
•
Oak
Person
Pet
Pinetree
Plant
Puppy
Rose
Whale
Woman
Zebra

28. Instances
• Individual entities that can populate any
number of classes.
• An instance that is a member of a class, is
necessarily also a member of all its
superclasses.

30. Exercise
Create these instances:

31. The semantic triple
• A semantic triple is a statement consisting
of three parts:
• an instance (subject)
• a property that refers to that instance
(predicate)
• a value for that property (object)
George likes chocolate
s
p
o

36. Properties
• The instances are described through properties.
• There are two different types of properties:
• Object property:
• Takes another instance as value
• e.g. Alice knows Fred
• Datatype property
• Takes a distinct datatype value, like a number, a string etc.
• e.g. King Harald has year of birth 1937
• The property is the ”predicate” in the semantic triple.

37. Domain and Range
• The domain and range of a property determine
what kind of instances it can be used for and what
kind of values it can have.
• Domain
• The class, whose instances can have the property
• If domain is not set, domain=Thing
• Range
• The class, whose instances can be value for an object
property
• The type of data that is allowed as value for a datatype
property

38. Properties of properties
• Properties can be:
• symmetric
(Martin has cousin Thomas) ⇔ (Thomas has cousin Martin)
• asymmetric
(Martin is father of Rosie) ⇒ (Rosie can not be father of Martin)
• inverse
(Martin is parent of Rosie) ⇔ (Rosie is child of Martin)
• transitive
(Rosie descends from Martin) and (Martin descends from Emma)
⇒ (Rosie descends from Emma)
• functional (can have only one value)
• inverse functional (value can be held by only one instance)
• reflexive (instance takes itself as a value)

39. Exercise
Object properties
• Create the following object properties
• owns
• ownedBy
• hasNeighbour
• Set domain and range
• Connect instances, so that:
• Mr. Taylor owns Duchess
• Mrs. Robertson owns Lassie
• Mr. Taylor and Mrs. Robertson are neighbours

40. Restrictions
• Classes can be populated according to rules
called restrictions.
• This is done by expressing that a class is
equivalent to a certain set of instances.
• The set can be defined by
• combining other classes with and/or/not
operators
• using criteria based on desired properties for
the instances

41. Restrictions
• Add new class LivingThing
• Use class expression editor to express
equivalence relation:
LivingThing
≡
Animal or Plant or Person

42. •
•
•
•
Add the class Gender
Add the individuals Male and Female
Add the property hasGender, domain: LivingThing
Express that:
•
•
•
•
•
•
Lassie is female
Duchess is female
Moby Dick is male
Mr. Taylor is male
Mrs. Robertson is female
Thomas O’Malley is male

43. • Add classes FemaleBeing and MaleBeing
• Use class expression editor to express
equivalence relations:
FemaleBeing ≡
MaleBeing
≡
Pet
≡
hasGender value Female
hasGender value Male
Animal and ownedBy some Person

44. What about this?
WildAnimal ≡
Animal and not (ownedBy some Person)

45. Open world assumption
• The truth-value of an assumption does not
depend on whether it is known or not
• The absence of a statement therefore does
not count as a negation of that statement

46. • Statements:
• Mary is a woman
• George is a man
• Mary is an American citizen
• Question:
• Is George an American citizen?
• Answers
• Closed world assumption:
• Open world assumption:
"No"
"Unknown"

47. Example ontologies
• Dublin Core metadata terms
http://purl.org/dc/terms/
• Bibo (Bibliographic ontology)
http://purl.org/ontology/bibo/
• Core FRBR
http://purl.org/spar/frbr/
• FOAF (Friend of a friend)
http://xmlns.com/foaf/spec/