The document discusses nuclear models, specifically the liquid drop model. It provides three key points:
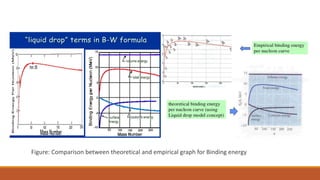
1. The liquid drop model views the nucleus as similar to a liquid drop, with nucleons interacting through short-range forces like molecules in a liquid. This explains trends in binding energy with mass number.
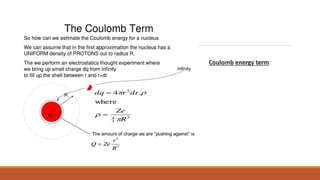
2. The Beithe-Weizsacker formula provides a semi-empirical expression for binding energy as a function of mass and atomic number. It includes terms for volume, surface tension, electrostatic repulsion and asymmetry.
3. The formula allows predicting stability against alpha or beta decay. Alpha decay energy can be calculated and nuclei with mass over 200 are predicted to alpha decay. Mass parabol

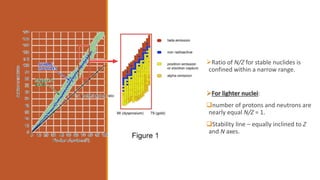
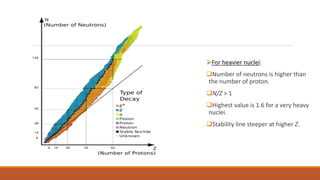
![Naturally occurring elements can be classified into two classes:
Elements[Natural]
Even values of Z Odd values of Z](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-2-320.jpg)






































![Alpha Decay:
If a nucleus ZXA undergoes 𝛼 – decay into the nucleus Z-2YA-4
ZXA
Z-2YA-4 + 2He4
The 𝛼 – disintegration energy –
𝑄𝛼 = M(A,Z) - M(A – 4, Z-2) – M[2He4]
written in terms of the binding energies 𝐸𝐵 of the nuclei involved:
𝑄𝛼 = 𝐸𝐵(A – 4, Z – 2) + 𝐸𝐵[2He4] - 𝐸𝐵 (A, Z)
= 𝑎1(𝐴 − 4) - 𝑎2(𝐴 − 4)2 3- 𝑎3
(𝑍−2)2
(𝐴 −4)1 3 - 𝑎4
(𝐴 −2𝑍)2
𝐴 −4
- 𝑎1𝐴 + 𝑎2𝐴2 3+ 𝑎3
𝑍2
𝐴1 3 + 𝑎4
(𝐴 −2𝑍)2
𝐴
+ 𝐸𝐵[2He4]](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-45-320.jpg)
![On simplification:
𝑄𝛼 = 28.3 - 4𝑎1 +
8
3
𝑎2 𝐴−1 3 +
4𝑎3𝑧
𝐴1 3 [1 -
𝑍
3𝐴
] -
4𝑎4
𝐴
(𝐴 −2𝑍)2
𝐴 −4
---------------------------------- [1]
Important note:
Pairing energy term has been neglected.
Binding energy of the 𝛼 – particle is taken to be 28.3 MeV.
Using the numerical values of 𝑎1, 𝑎2, 𝑎3, 𝑎4 expressed in MeV are used in equation [1] gives
𝑄𝛼 >0 for A > 160.
Nuclei with A > 160 should be 𝛼 – disintegrating according to equation [1]
Observation: Nuclei with A > 200 undergo 𝛼 – disintegration.
For light nuclei (A < 200) the energy release is so small that barrier penetration probability is very
small.](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-46-320.jpg)
![Mass Parabolas: Stability of Nuclei against 𝜷 – Decay:
M(A,Z) = Z 𝑀𝐻 + (A – Z)𝑀𝑛 - 𝑎1𝐴 + 𝑎2𝐴2 3+ 𝑎3
𝑍2
𝐴1 3 + 𝑎4
(𝐴 −2𝑍)2
𝐴
Above equation can be rewritten as:
M(A,Z) = 𝑓𝐴 + pZ + q 𝑍2
------------------------------------------------------[1]
where 𝑓𝐴 = A(𝑀𝑛 - 𝑎1+ 𝑎4) + 𝑎2 𝐴2 3
p = -4𝑎4 - (𝑀𝑛 - 𝑀𝐻)
q =
1
𝐴
(𝑎3 𝐴2 3
+ 4𝑎4)
Equation [1] is the equation to a parabola for a given A.](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-47-320.jpg)










![From equation (1) and (2):
M(A,Z) - M(A,Z - 1) = 𝑀𝐻 - 𝑀𝑛 + 𝑎3
(2𝑍 −1)
𝐴1 3
𝑄
β
+ = [M(A,Z) - M(A,Z-1) - 2𝑚𝑒]
= 𝑀𝐻 - 𝑀𝑛 + 𝑎3
(2𝑍 −1)
𝐴1 3 - 2𝑚𝑒
= 𝑎3 𝐴2 3 - (𝑀𝑛 - 𝑀𝐻 + 2𝑚𝑒)
𝑸
β
+ = 𝒂𝟑 𝑨𝟐 𝟑 + 1.804 MeV](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-58-320.jpg)


![In spontaneous fission a nucleus ZXA undergoes the spontaneous transformation:
ZXA
𝑍1
𝐴1
𝑋1 + 𝑍2
𝐴2
𝑋2
where the two product nuclei have mass numbers and atomic numbers of comparable values.
𝐴1 + 𝐴2 = 𝐴 and 𝑍1 + 𝑍2 = 𝑍
𝐴1 = 𝐴2 = 𝐴/2 and 𝑍1 = 𝑍2 = 𝑍/2 -------------[Symmetric Fission]](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-61-320.jpg)

![For 𝑄𝑓 to be positive 𝑓𝐵
′
> 𝑓𝐵
Binding fraction of the product nuclei > binding fraction of the parent nucleus.
In terms of the semi – empirical mass formula:
M(A,Z) = Z 𝑀𝐻 + (A – Z)𝑀𝑛 - 𝑎1𝐴 + 𝑎2𝐴2 3+ 𝑎3
𝑍2
𝐴1 3 + 𝑎4
(𝐴 −2𝑍)2
𝐴
---------------------------[1]
M(A/2,Z/2) = Z/2 𝑀𝐻 + N/2𝑀𝑛 - 𝑎1(𝐴/2) + 𝑎2(𝐴/2)2 3+ 𝑎3
(
𝑍
2
)2
(𝐴/2)1 3 + 𝑎4
(𝐴 −2𝑍)2
2𝐴
------- [2]](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-63-320.jpg)



![Stability Limit Against Spontaneous Fission:
[Neutron bombarded on a target nucleus and gets captured.
Distorts spherical shape and induces oscillations.]
[Deviation from spherical shape [ redistribution of electric charges gives
tendency to move far apart]
Activation energy not sufficient, Surface energy > Coulomb energy [nucleus
retains its shape]]
Dumbbell shape [Surface energy < Coulomb energy fission takes place]](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-67-320.jpg)


![If 𝑎2 = 𝑎3 = ……….= 0, the nucleus is undistorted sphere for which R = 𝑅0.
UNDISTORTED NUCLEI DISTORTED NUCLEI
COULOMB ENERGY TERM [𝐸𝐶
0
] 𝑎3
𝑍2
𝐴1 3 =
0.71 𝑍2
𝐴1 3 (MeV) 𝐸𝐶
0
[ 1 -
𝑎2
2
5
- ……]
SURFACE ENERGY TERM [𝐸𝑆
0
] 𝑎2𝐴2 3
= 17.80 𝐴2 3
(MeV) 𝐸𝑆
0
[ 1 +
2𝑎2
2
5
+ …..]](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-70-320.jpg)




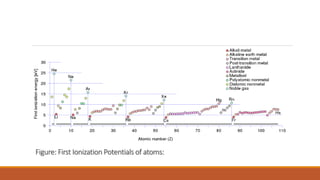
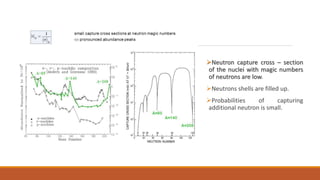
![Nuclear Shell Structure:
Different nuclear models proposed explain limited features of the nuclei.
Liquid Drop Model explains:
Observed variation of the nuclear binding energy with mass number,
Fission of the heavy nuclei.
Liquid Drop Model predicts:
Closed spacing of the energy levels in the nuclei [at low energies]](https://image.slidesharecdn.com/nuclearmodels-210427062304/85/NUCLEAR-MODELS-75-320.jpg)