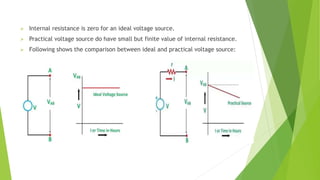
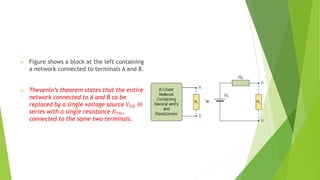
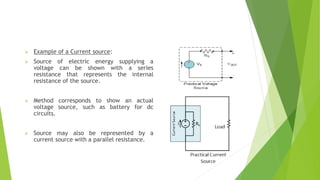
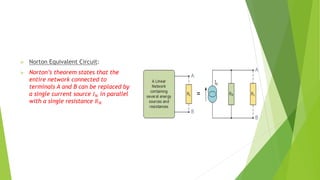
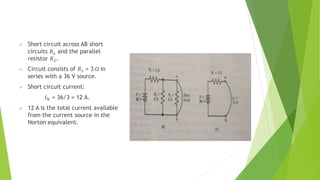
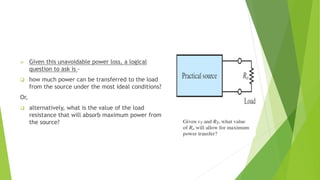
The document discusses several network theorems including superposition, Thevenin's, and Norton's theorems. Superposition theorem states that the total response of a network with multiple sources is the sum of the responses of each source acting alone. Thevenin's theorem shows that any linear network can be reduced to an equivalent circuit with a voltage source and single output resistance. Norton's theorem represents a network as a current source and parallel output resistance. Both theorems simplify analysis of complex networks. Maximum power transfer occurs when the load and source resistances are equal.

1. Chapter 2: NETWORK THEOREMS
 Ideal Voltage Source and Ideal Current Source:
 Ideal Voltage Source:
 An ideal voltage source provides a prescribed voltage across its terminals
irrespective of the current flowing through it. The amount of current supplied
by the source is determined by the circuit connected to it.
 Example: Battery, Alternator

2.  Internal resistance is zero for an ideal voltage source.
 Practical voltage source do have small but finite value of internal resistance.
 Following shows the comparison between ideal and practical voltage source:

3.  Ideal Current Source:
 An ideal current source provides a prescribed current to any circuit connected
to it. The voltage generated by the source is determined by the circuit
connected to it.
 Example: Photoelectric cell , Collector current of a transistor.

4.  Comparison between an ideal and a practical current source:

5. SUPERPOSITION THEOREM:
 Superposition theorem extends the use of Ohm’s law to circuit that have more
than one source.
 In short, we can calculate the effect of one source at a time and then
superimpose the results of all the sources.
 Superposition Theorem:
 In a network with two or more sources, the current or voltage for any
component is the algebraic sum of the effects produced by each source acting
separately.

6.  In order to use one source at a time:
 All other sources are “killed” temporarily.
 It means disabling the source so that it cannot generate voltage or current,
without changing the resistance of the circuit.
 Voltage source such as a battery can be disabled by assuming a short circuit
across its potential difference.
 Internal resistance remains (if any).

7.  Example 1: Voltage divider with two sources.
 To find: Voltage at point P to chassis ground for the circuit.
 Solution:
 Methodology:
1) To calculate the voltage at P contributed by each source separately.
2) Superimpose these voltages.

8.  To find the effect of 𝑉1:
 Short circuit 𝑉2.
 Bottom of 𝑅1 then becomes connected to chassis
ground because of the short circuit 𝑉2.
 𝑅2 and 𝑅1 form a series voltage divider for source
𝑉1.
 Voltage across 𝑅1= voltage from P to the ground.
 To find 𝑉𝑅1
across 𝑅1, the contribution of the
source 𝑉1, we can use voltage – divider formula:
𝑉𝑅1
=
𝑅1
𝑅1+𝑅2
𝑋 𝑉1 = 16 V

9.  To find the effect of 𝑉2 alone:
 Short circuit 𝑉1.
 Point A at the top becomes grounded.
 𝑅2 and 𝑅1 form a series voltage divider.
 𝑅2 voltage is the voltage at P to the ground.
 With one side of 𝑅2 grounded and the other to point
P, 𝑉𝑅2
is the voltage to be calculated.
 Using the voltage divider formula for 𝑉𝑅2
as the
contribution of 𝑉2 to the voltage at P:
𝑉𝑅2
=
𝑅2
𝑅1+𝑅2
𝑋 𝑉2 = -3V

10.  Voltage at P:
𝑉𝑃 = 𝑉1 + 𝑉2 = 16 – 3 = 13 V.
 Conclusion:
 Algebraic sum is positive for the net 𝑉𝑃 because the positive 𝑉1 is larger than
the negative 𝑉2.
 By Superposition theorem, the problem was reduced to two series voltage
dividers.
 Same procedure can be applied for circuit with two or more sources.
 Each voltage divider can have any number of series resistance.

11. Thevenin’s Theorem:
 Named after M.L. Thevenin, a French engineer.
 Useful in simplifying the process of solving unknown values of voltages and
current in the network.
 By Thevenin’s theorem, many sources and components, no matter how they
are interconnected, can be represented by an equivalent series circuit with
respect to any pair of terminals in the network.

12.  Figure shows a block at the left containing
a network connected to terminals A and B.
 Thevenin’s theorem states that the entire
network connected to A and B ca be
replaced by a single voltage source 𝑉𝑇𝐻 in
series with a single resistance 𝑅𝑇𝐻,
connected to the same two terminals.

13.  To find the Thevenin Voltage 𝑉𝑇𝐻:
 𝑉𝑇𝐻 is the open circuit voltage across the terminals A and B.
 Implies to find the voltage that the network produces across the two
terminals with an open circuit between A and B.

14.  To find the Thevenin Resistance 𝑅𝑇𝐻:
 Resistance 𝑅𝑇𝐻 is the open circuit resistance across terminals A and B, but
with the sources killed.
 Implies to find the resistance looking back into the network from terminals A
and B.
 With terminals open an ohmmeter across AB would read the value of 𝑅𝑇𝐻 as
the resistance of the remaining paths in the network, without any sources
operating.

15.  Example: Thevenizing a Circuit:
 Problem: In the given figure, we wish to
calculate the voltage 𝑉𝐿 across the 2 Ω and its
current 𝐼𝐿.
 Data: V = 36 V, 𝑅1 = 3 Ω , 𝑅2 = 6 Ω , 𝑅𝐿 = 2 Ω

16.  To find:
1) To find the value of the open – circuit voltage
𝑉𝑇𝐻 across AB.
2) Equivalent resistance 𝑅𝑇𝐻.
 Solution:
 To find 𝑉𝑇𝐻:
 Effect opening 𝑅𝐿: 𝑅1 = 3 Ω and 𝑅2 = 6 Ω form
a series voltage divider network without 𝑅𝐿.
 Voltage across 𝑅2 is the same as the open –
circuit voltage across terminals A and B.

17.  𝑉𝑅2
with 𝑅𝐿 open is 𝑉𝐴𝐵. (this is the 𝑉𝑇𝐻 for Thevenin equivalent circuit)
 By Voltage – divider formula:
𝑉𝑅2
=
6
9
𝑋 36 𝑉 = 24 𝑉
𝑉𝑅2
= 𝑉𝐴𝐵 = 𝑉𝑇𝐻 = 24 V.
 Voltage is positive at terminal A.

18.  To find 𝑅𝑇𝐻:
 2 Ω 𝑅𝐿 is disconnected.
 Source V is short circuited.
 𝑅1 = 3 Ω and 𝑅2 = 6 Ω parallel to each
other.
 Combined resistance:
𝑅𝑇𝐻 =
18
9
= 2 Ω.

19.  Thevenin circuit to the left of terminals A
and B consists of the equivalent voltage 𝑉𝑇𝐻
equal to 24 V in series with the equivalent
series resistance 𝑅𝑇𝐻 equal to 2 Ω.
 Thevenin equivalent circuit applies to any
value of load 𝑅𝐿.

20.  To find 𝑉𝐿 and 𝐼𝐿:
 Reconnect 𝑅𝐿 to the terminals A and B of the Thevenin equivalent circuit.
 𝑅𝐿 is in series with 𝑅𝑇𝐻 and 𝑉𝑇𝐻.
 By voltage divider formula: for the 2 Ω 𝑅𝑇𝐻 and 2 Ω 𝑅𝐿,
𝑉𝐿 = ½ X 24 V.
 To find 𝐼𝐿:
𝐼𝐿 = 𝑉𝐿/𝑅𝐿 = 6A.

21.  Same answers will be obtained by solving the series – parallel circuit using
Ohm’s law.
 Advantage of Thevenizing the circuit:
 Effect of different values of 𝑅𝐿 can be calculated easily.
 For example: if 𝑅𝐿 = 4 Ω is changed to the new value of 𝑉𝐿= 16 V and 𝐼𝐿 = 4 A.
 If we use Ohm’s law in the original circuit, a complete new solution would be
required each time 𝑅𝐿 is changed.

22.  Example 2:

23. Norton’s Theorem:
 Named after E.L. Norton. (Scientist with Bell Telephone Laboratories)
 Theorem used for simplifying a network in terms of currents instead of
voltages.
 Current analysis more easier than voltage analysis in many cases.
 For current analysis: Norton’s theorem can be used to reduce a network to a
simple parallel circuit, with a current source.

24.  NOTE:
 A current source supplies a total line current to be divided among parallel
branches, corresponding to a voltage source applying a total voltage to be
divided among series components.

25.  Example of a Current source:
 Source of electric energy supplying a
voltage can be shown with a series
resistance that represents the internal
resistance of the source.
 Method corresponds to show an actual
voltage source, such as battery for dc
circuits.
 Source may also be represented by a
current source with a parallel resistance.

26.  If the current I, is a 2 – A source, it supplies 2 A no matter what is connected
across the output terminals.
 Without anything connected across the output terminals, all the 2 A flows
through the shunt R.
 When a load resistance 𝑅𝐿is connected across the output terminals, the
current 2 A divides according to the current division for the parallel branches.

27. Comparison between Voltage Source and Current Source:
Voltage Source
 Voltage source is disabled by short
circuiting.
 A voltage source is short circuited
to kill its ability to supply voltage
without affecting any series
components.
Current Source
 Current source is killed by making
it open.
 Opening a current source kills its
ability to supply current without
affecting any parallel branch
currents.

28.  Norton Equivalent Circuit:
 Norton’s theorem states that the
entire network connected to
terminals A and B can be replaced by
a single current source 𝐼𝑁 in parallel
with a single resistance 𝑅𝑁

29.  Value of 𝐼𝑁 is equal to the short circuit current through the output terminals.
 This means to find the current that the network would produce through A and
B with a short circuit across these two terminals.
 Value of 𝑅𝑁 is the resistance looking back from the open output terminals.
 Output terminals are not short circuited for 𝑅𝑁 but are open output
terminals.

30.  Nortonizing a Circuit:
 Example: Figure (a)
 Solution:
 Step 1:
 Imagine a short circuit across the terminals
A and B.
 How much current is flowing in the short
circuit??

31.  Short circuit across AB short
circuits 𝑅𝐿 and the parallel
resistor 𝑅2.
 Circuit consists of 𝑅1 = 3 Ω in
series with a 36 V source.
 Short circuit current:
𝐼𝑁 = 36/3 = 12 A.
 12 A is the total current available
from the current source in the
Norton equivalent.

32.  To find 𝑅𝑁:
 Remove the short circuit across A and B.
 Consider the terminals open without 𝑅𝐿.
 Source V is considered to be short circuited.
 Resistance seen as looking back from
terminals A and B is 6 Ω ||3 Ω equal to 2 Ω.

33.  Resultant Norton’s equivalent consists of 12-A
current source 𝐼𝑁 shunted by the 2 Ω 𝑅𝑁.
 To calculate 𝐼𝐿:
 Replace the 2 Ω 𝑅𝐿 between terminals A and
B.
 Current delivered in the circuit 12 A: this
current divides between the two branches of
𝑅𝑁 and 𝑅𝐿.
 Since the two resistances are equal the
current 12 A divides into 6 A for each branch.
 𝐼𝐿 = 6 A.

34. Maximum Power Transfer:
 Reduction of a linear resistive network to its equivalent Norton or Thevenin
form is useful for –
 Computation of load – related quantities.
 Computation of power absorbed by the load.
 The Thevenin and Norton models imply that -
 some of the power generated by the source will necessarily be dissipated by
the internal circuits within the source.

35.  Given this unavoidable power loss, a logical
question to ask is -
 how much power can be transferred to the load
from the source under the most ideal conditions?
Or,
 alternatively, what is the value of the load
resistance that will absorb maximum power from
the source?

36.  The model employed in the discussion of power
transfer is illustrated in figure -
 Practical source is represented by means of its
Thevenin equivalent circuit.
 Maximum power transfer problem is easily formulated
if we consider that the power absorbed by the load
(𝑃𝐿)
𝑃𝐿 = 𝑖𝐿
2
𝑅𝐿
 load current is given by the expression:
𝑖𝐿 =
𝑣𝑇
𝑅𝐿+𝑅𝑇

37.  Load power –
𝑃𝐿 =
𝑣𝑇
2
(𝑅𝐿+𝑅𝑇)2
 To find the value of 𝑅𝐿 that maximizes the expression for 𝑃𝐿(with 𝑣𝑇 and 𝑅𝑇
fixed), using the maximization problem:
𝑑𝑃𝐿
𝑑𝑅𝐿
= 0
 On simplifying –
𝑅𝐿 = 𝑅𝑇
 Conclusion: In order to transfer maximum power to a load, the equivalent
source and load resistances must be matched, that is, equal to each other.

38.  Example:
 A problem related to power transfer is that
of source loading. This phenomenon, which
is illustrated in Figure, may be explained as
follows:
 Practical voltage source connected to a
load, the current that flows from the source
to the load will cause a voltage drop across
the internal source resistance,𝑣𝑖𝑛𝑡.
 Voltage seen by the load will be somewhat
lower than the open-circuit voltage of the
source.
 Open-circuit voltage is equal to the
Thevenin voltage.
 Extent of the internal voltage drop within
the source depends on the amount of
current drawn by the load.

39.  With reference to given figure, this
internal drop is equal to 𝑖𝑅𝑇 , and
therefore the load voltage will be –
 It is desirable to have as small an internal
resistance as possible in a practical voltage
source