1) Impulsive differential equations are used to model systems with abrupt changes like shocks or disasters and involve short-term perturbations interrupting otherwise smooth dynamics.
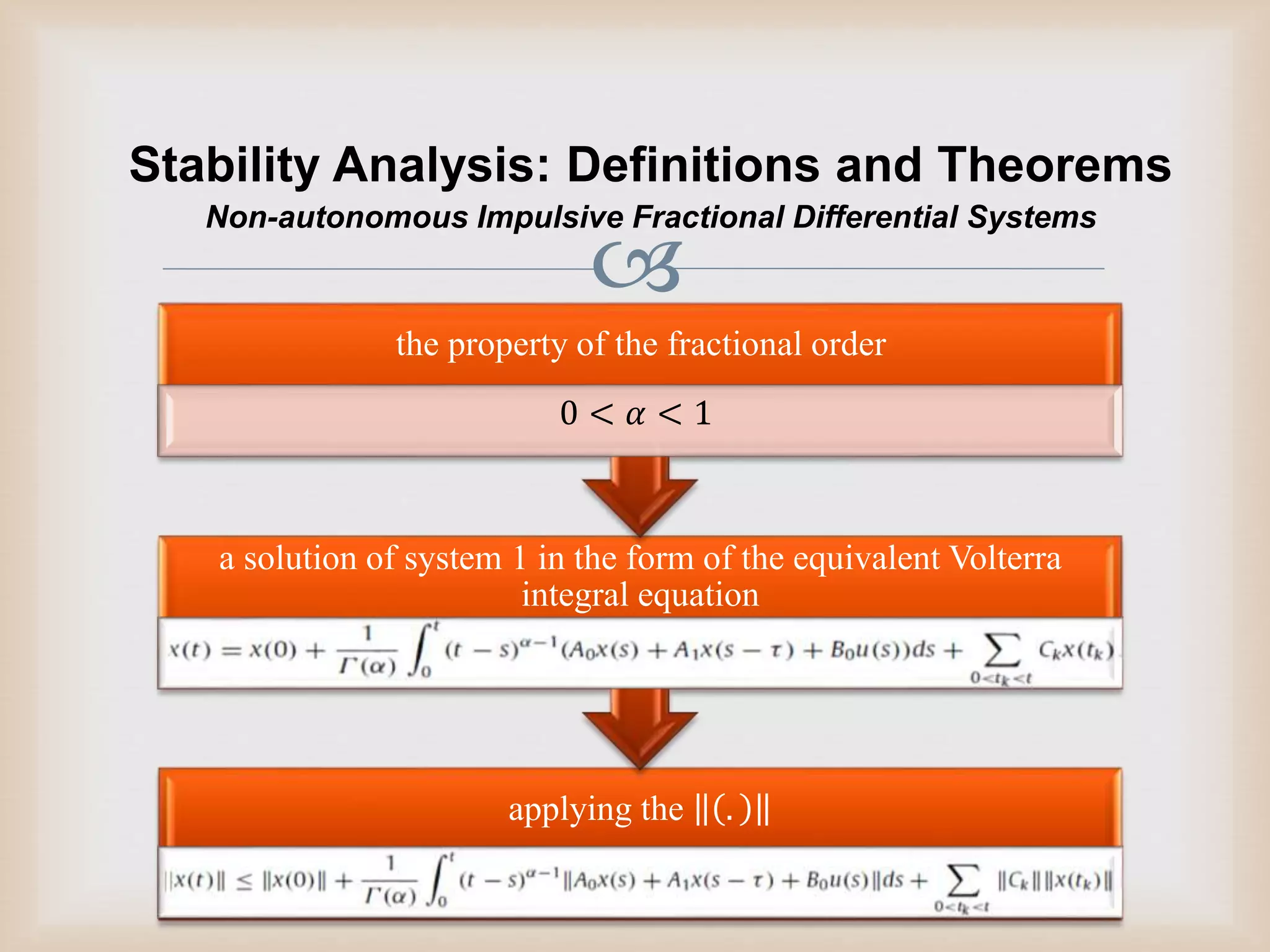
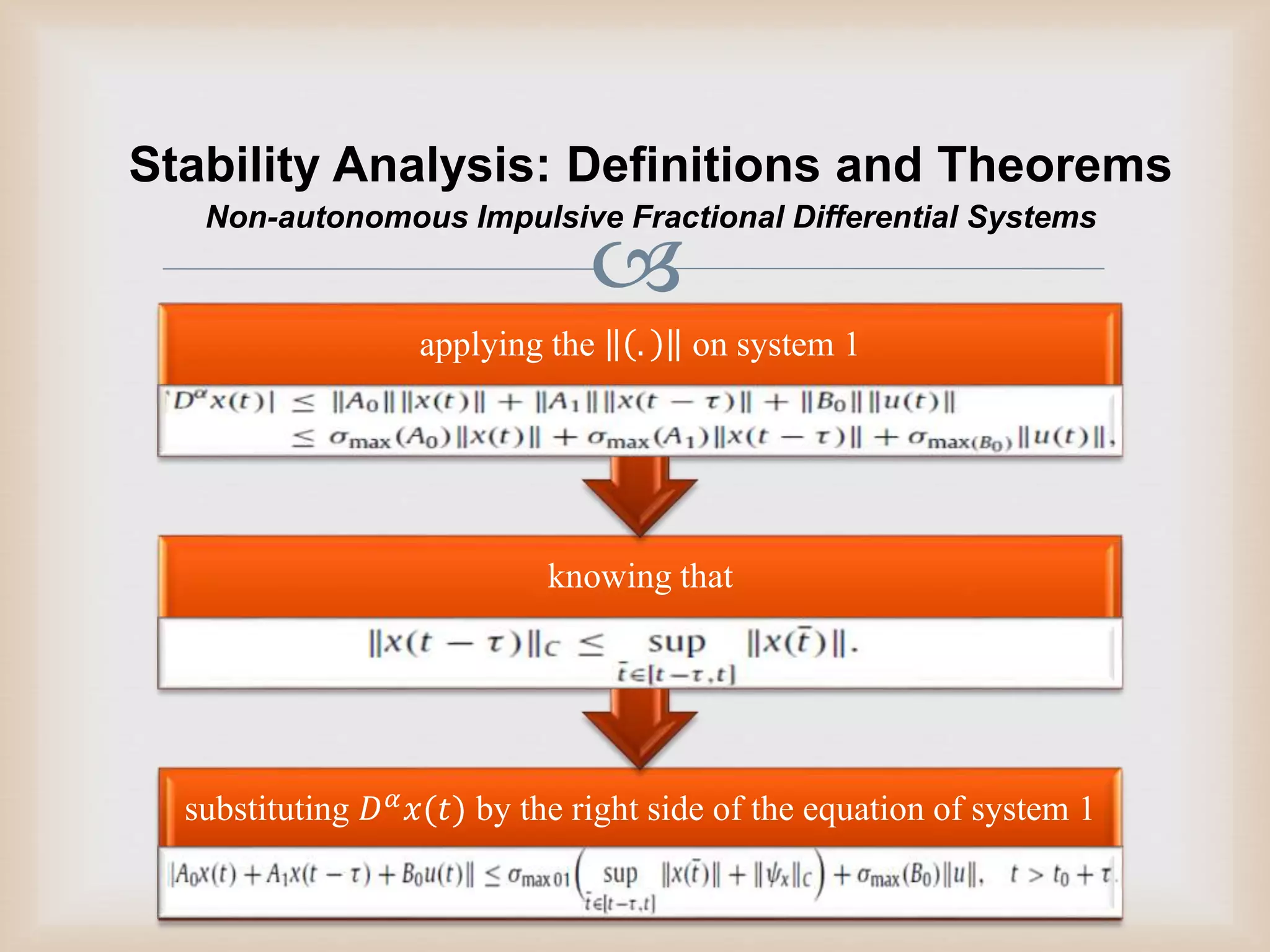
2) Stability of delayed impulsive fractional differential systems is analyzed using Gronwall inequalities, which provide bounds on solutions to integral inequalities.
3) Three main approaches are presented to analyze the stability of non-autonomous delayed impulsive fractional differential systems using Gronwall inequalities and the Mittag-Leffler function.




![
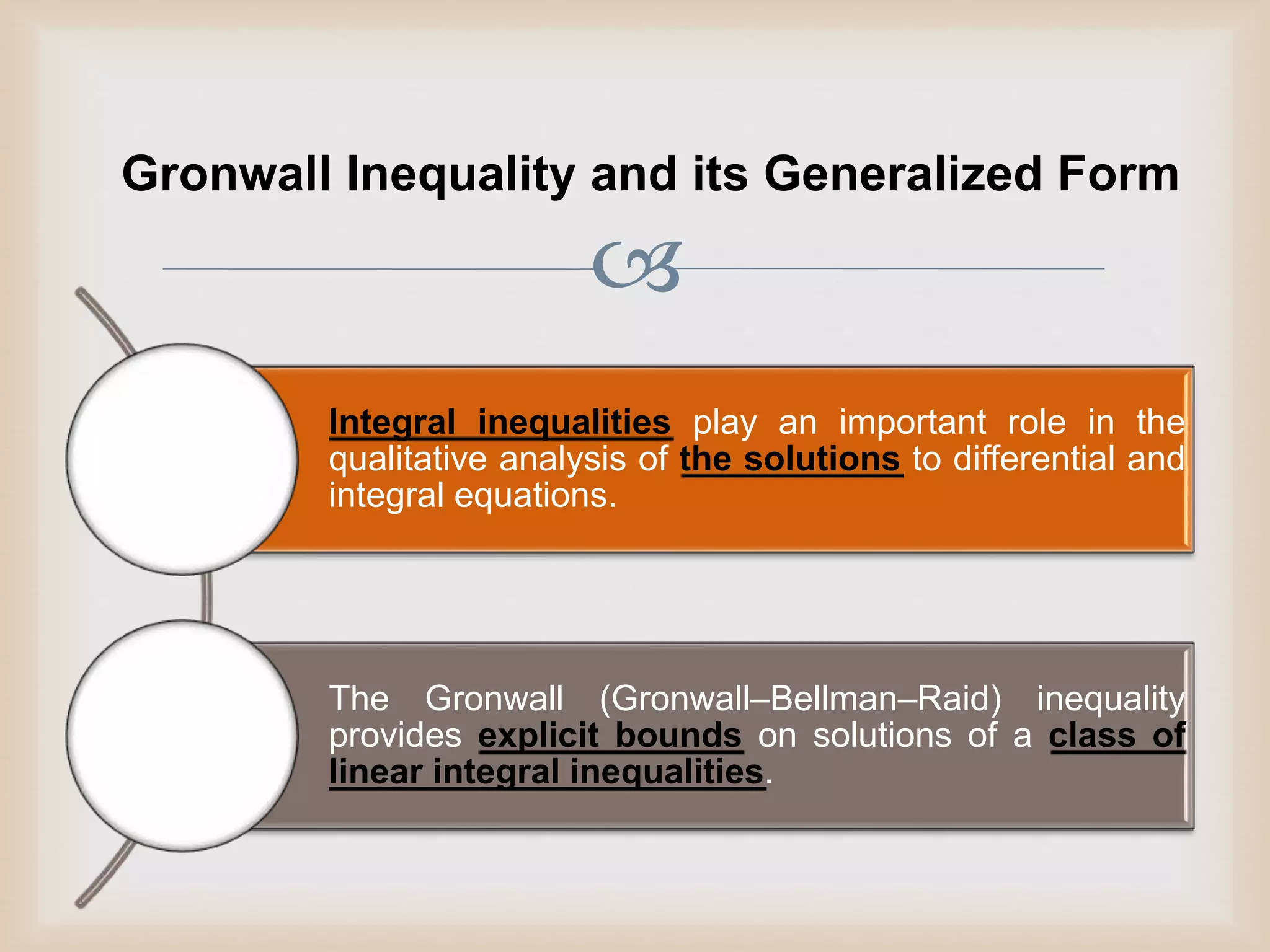
Gronwall Inequality and its Generalized Form
If
𝑥 𝑡 ≤ ℎ 𝑡 +
𝑡0
𝑡
𝑘 𝑠 𝑥 𝑠 𝑑𝑠 , 𝑡 ∈ 𝑡0, 𝑇 ,
where all the functions involved are continuous on 𝑡0, 𝑇 , 𝑇
≤ +∞, and 𝑘(𝑡) ≥ 0, then 𝑥 𝑡 satisfies
𝑥 𝑡 ≤ ℎ 𝑡 +
𝑡0
𝑡
ℎ(𝑠)𝑘 𝑠 exp[
𝑠
𝑡
𝑘 𝑢 𝑑𝑢]𝑑𝑠 , 𝑡 ∈ 𝑡0, 𝑇 .
The
Standard
Gronwall
Inequality](https://image.slidesharecdn.com/stabilityanalysisofimpulsivefractionaldifferentialsystemswithdelay-141230063309-conversion-gate02/75/Stability-analysis-of-impulsive-fractional-differential-systems-with-delay-6-2048.jpg)


![
Gronwall Inequality and its Generalized Form
Suppose 𝑥 𝑡 and 𝑎 𝑡 are nonnegative and locally
integrable on 0 ≤ 𝑡 < 𝑇 (some 𝑇 ≤ +∞), and 𝑔(𝑡) is a
nonnegative, nondecreasing continuous function defined
on 0 ≤ 𝑡 < 𝑇, 𝑔 𝑡 ≤ 𝑀 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡, and 𝛼 > 0 with
𝑥 𝑡 ≤ 𝑎 𝑡 + 𝑔(𝑡)
0
𝑡
(𝑡 − 𝑠) 𝛼−1
𝑥 𝑠 𝑑𝑠
on this interval. Then
𝑥 𝑡 ≤ 𝑎 𝑡 + 𝑔(𝑡)
0
𝑡
[
𝑛=1
∞
(𝑔(𝑡)𝛤(𝛼)) 𝑛
𝛤(𝑛𝛼)
(𝑡 − 𝑠) 𝑛𝛼−1 𝑎(𝑠)]𝑑𝑠
The
Generalized
Gronwall
Inequality](https://image.slidesharecdn.com/stabilityanalysisofimpulsivefractionaldifferentialsystemswithdelay-141230063309-conversion-gate02/75/Stability-analysis-of-impulsive-fractional-differential-systems-with-delay-9-2048.jpg)