1. The document provides solutions to math problems involving sets, logic, trigonometry, vectors, and calculus. 2. Several problems are solved involving intersections of sets, logical statements, trigonometric identities, and vector operations. 3. Solutions include determining the intersection of two sets, evaluating logical statements, simplifying trigonometric expressions, and calculating the cross product of two vectors.

1. 76
14 F A-NET
1: F 25 F F 3
1. F A = { x | 0166xx2
≤−− }
B = { x | 5x2 <− }
F A B = [a, b] F a + b F F F
1. 15 2.16 3.17 4.18
2. F F
. F F )1,2( −−
F 0]32xx[x2
<−+∀ F ˈ
. F ∀x[P(x)→ [Q(x) →R(x)]
∃x[P(x) ∧ Q(x) ∧∼R(x)]
F F F
1. . . 2. . . 3. . . 4. . .
3. F F ˈ F F F ˈ
1. 0]}x[x0]x[x{0)](x0)x[(x ≤∀∨>∀→≥∨<∀
2. 0)](x0)x[(x0]}x[x0]x[x{ ≤∧>∃→≤∃∧>∃
3. 0]}x[x0]x[x{0)](x0)x[(x >∀→>∃→>→>∀
4. 0]}x[x0]x[x{0)](x0)x[(x >∀→>∀→>→>∀
4. F }
43x
12x
yRRy),{(xr
+
+
=×∈=
}
x9
4x
yRRy),{(xs 2
2
−
−
=×∈=
F F ˈ sr RR ∩
1. )
3
2
,
9
4
[1),(
−
∪−−∞ 2. ),
3
2
()
3
2
,
9
4
[ ∞∪
−
3. ),
3
2
()
3
2
,
9
4
[1),( ∞∪
−
∪−−∞ 4. ),
9
4
[1),( ∞
−
∪−−∞
5. F 134xh(x) +−=
2
5x
(x)g 1 +
=−
F F g ˈ ˆ F F gof = h F f(1.3) F F F F
1. 6.4 2. 6.8 3. 6.0 4. 6.2
6. F A B ˈ F A = 




 −
a1
20
, a ˈ
F BA = A-1
det (4B - I) = 0 F a F F F F F
1. 1 2. 2 3. 3 4. 4
7. FP ˈ 078x2yy2
=−−− l ˈ F F F F
P l ˈ F F F
1. 0142222
=−−++ yxyx 2. 022222
=−−++ yxyx
3. 022222
=−+++ yxyx 4. 0142222
=−+++ yxyx

2. 77
8. F F )
5
18
(3, F F 04812yy3x 22
=−+− F F
1. F F 2,6)(−
2. F ( ) F 7 F
3. 3 F
4. F 4 F
9. F A = {x| 2x1xx1xx
22266 +++
++=+ }
B = {x| 01)(2xlogloglog 327 =− }
A B F F
1. 0 2. 1 3. 2 4. 3
10. F A(3, 5, 2) , B(1, -1, 6) C(-2,1, 4)
1. 21 2. 3 21 3. 5 21 4. 7 21
11. F u
v
= 3 i
v
4 j
v
v
v
= i
v
+ j
v
F F F F
1. F u
v
+ 2 v
v
30° F u
v
2 v
v
2. F F u
v
2 v
v
6 i
v
+ j
v
3. F F F F u
v
+ v
v
5
4−
i
v
+
5
3
j
v
4. | u
v
v
v
| ≥ | u
v
+ v
v
|
12. F f(x) = sin x g(x) = arcsin 2x + 2 arcsin x F F (fog)(
3
1
) F F
1.
9
4
2.
9
2
(1 + 8 ) 3. 4 2 +
12
10
4.
27
2
(7 + 2 10 )
13. F ABC ˈ F Aˆ , Bˆ , Cˆ a, b,c
F sinC)sinBsinC)(sinAsinB(sinA −+++ = 3sinAsinB F Cos C F F
1.
2
1
2.
2
3
3.
2
2
4. 1
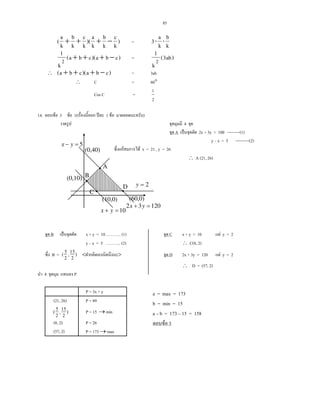
14. F F P = 3x + y
F 2x + 3y ≤ 120
x + y ≥ 10
y x ≤ 5
y 2 ≥ 0
F a ˈ F b ˈ F F P F a b F F F
1. 158 2. 173 3. 89 4. 15
15. F Z 1 = -1 - 3 i (z 2)3
=
2
1
+
2
i3
F F Z1
6
+ (Z 2) 27
F F
1. 31 2. 26 3. 63 4. 127
16 F z ˈ F | zaiz +−1
4 | = 652 |z| F F F F
1. 1],
2
1
( 2. ]
2
1
,0( 3. ]
2
3
,(1 4. 2],
2
3
(

3. 78
17. 8 ˈ 6 ˈ F3 3 2 ˈ F
1 1 F F F 4 F F ˈ F F F
0 ˈ F F F
1.
70
14
2.
70
10
3.
70
28
4.
70
1
18. F 3 4 5 F F 2 F F ˈ
F 2 F F
1.
11
1
2.
66
10
3.
66
19
4. F ˈ F
19. F
. 2,2602019...54433221 =⋅++⋅+⋅+⋅+⋅
. F 2n
n1n
n
21
22
a +
+
+
−
= F
4
1
alim n
n
=
∞→
F F F
1. . . 2. . F . 3. . F . 4. . .
20. F a ˈ
F f(x) =




≤−
>
−
−
3x,6aax
3x,
33x
a3x
2
F f ˈ ˆ F F F f′(a) F F F F
1. 2 2. 4 3. 8 4. 10
21. F f(x) = 13x + F g ˈ ˆ F 1)( 2
+= xxgf o x ∈ R F f′(1) + g′(1)
F F F F
1.
12
41
2.
12
35
3.
4
33
4.
4
39
22. F a F ʽ F F F F 104axxay 22
++= x = 0 x = 1 F F
F F ˈ F
1. 5 2. 7 3. 9 4. 11
23. F
F
96 105
86 95
76 85
66 75
56 65
46 55
3
7
10
y
x
4
F F 65.5Q1 = F 75.5 F F F F F F F
1. 5 2. 10 3. 15 4. 20

4. 79
24. F Xi ˈ i i = 1, 2, 3, ..., 99, 100 F 100 F F
F F 70, 40 60 F F
1. ∑ −
=
100
1i
i 60X F ∑ −
=
100
1i
i 70X
2. ( )∑ −
=
100
1i
2
i 70X F ( )∑ −
=
100
1i
2
i 40X
3. F ˈ F F F
4. F F F F 60 F F F F
60 ˈ F F
25. F F F F 0 z
Z 0.35 0.71 1.00 2.00
A 0.136 0.261 0.341 0.477
F F 2 F F F F F F F
F 60 F 12 F F 70 F
7 F F F F F 36 F F F
F F 63 X F X F F
1. 63.45 2. 72.45 3. 68.45 4. 78.45
2: F 10 F F 1 5 F 2
F 6 10 F 3
1. F x ˈ F 9, 12 15 x F 11 x 7 F x F F F
1. 1400 2. 1600 3. 1800 4. 2000
2. F F F 16x 2
- 9y 2
+ 32x +36y =164 x x1 , x2 F F x1 , x2
F
1. 0.5 2. 1 3. 2 4. 3
3. F log 2 3 = 159 F F x F 2 12 +x
· 3 22 +x
= 12 x2
1. 2.09 2. 2.25 3. 2.75 4. 3.00
4. F A =










−10x
113
11x
F C12 (A) = 4 F det (2A) F F
1. 15 2. 16 3. 17 4. 18
5.
1
lim
→x






+−
−
− 2
x3x2
1
x1
1
F F
1. 0.25 2. 0.55 3. 1 1. 25
6. F I ˈ F 0269x2xI{xS 2
≤−−∈= 3}2x1 ≥−
F S F F
1. 14 2. 15 3. 16 4. 17

5. 80
7. F 5
x1h(x) −= 5
xg(x) = F f ˈ ˆ F h(x)f(g(x)) = F f(5)
F F
1. 1 2. 2 3. 3 4. 4
8. F(x 1 + i) (x + 2) ˈ ˆ F f(x) = x3
+ ax 2
+ bx + c(x -3) f(x) F
1. 17 2. 20 3. 23 4. 25
9. F F F 0.12 F F 6 F F
10 F F F F
1. 1.05 2. 0.05 3. 0.20 4. 0.25
10. F F ˆ F F F x y ˈ F
∑=
8
1i
ix = 32 , ∑=
8
1i
iy = 16 ∑=
8
1i
ix yi = 65 ∑=
8
1
2
1
i
x =140 ∑=
8
1
2
i
iy = 34, F x = 8 F F y F F
1. 1.33 2. 2.33 3. 1.75 4. 2.75

6. 81
HE cc =
Ha
A B D F EF′ )6,0(C
14 F A-NET
1
1. F 1 F F F F F F
A 166xx2
−− ≤ 0 B | 2 x | < 5
(x 8) (x + 2) ≤ 0 | x 2 | < 5
5 < x 2 < 5
2 8 3 < x < 7
A = [2, 8] B = (3, 7)
A B = [7, 8] = [a, b]
a + b = 7 + 8 = 1
2. F 4
3. F 4
4. F 3
5. F 1
6. F 3
7. F 4
8. F 3 F F F
F
F F 04812yy3x 22
=−+−
3648)612y(y)3(x 222
−=+−−
12 1
12
6)(y
4
0)(x 22
=
−
−
−
F F )6,(0k),(h == , 4c,12b,2a ===
F F F x F
F F F F
+ +
|a b| = |b a|
F
3
2 8
A
B
A B
87
7

7. 82
F 1
F F F F F F F F 2 F
∴ 6),(26),2(0D,B =±= 6),2(−
F 2-4 Eb F ˈ x F
6),(0k),(h == 16bcba,4cc 2
E
2
E
2
E
2
EHE +=+===
1
b
k)(y
a
h)(x
2
2
2
2
=
−
+
−
1
)6(
16 2
2
2
2
=
−
+
+ EE b
y
b
x
F )
5
18
,(3 F
1
b
6)
5
18
(
16b
9
2
E
2
2
E
=
−
+
+
---------------------(2)
F F Eb F F F F F F F F 3 F F F
2
3
bE = F ( 2b ) (2)
1
4
9
)
5
12
(
16
4
9
9
2
=
−
+
+
1)
25
144
(
9
4
13
36
=+ ˈ ∴ F 3
F F F F
F F 3bE = F (1) ˈ
62bE == F
10)1692(2aE =+== F
F 4610 =−= F
F ( ) AD= BE
CDAC +=
hE aa +=
725 =+=
9. F 4
10. F 2 AB = -2 i
v
- 6 j
v
+ 4 k
v
AC = -5 i
v
- 4 j
v
+ 2 k
v
AB× AC =
245
462
kji
−−
−−
vvv
= (-12 16) i
v
- (-4 + 20) j
v
+ (8 30) k
v
= 4 i
v
- 16 j
v
- 22 k
v

8. 83
| AB× AC | = 48425616 ++ = 756 = 6 21
. . ∆ ABC = 3 21
11. F 1 u
v
= 3 i
v
4 j
v
v
v
= i
v
+ j
v
1. F Q 2 u
v
+ v
v
= 2(3 i
v
4 j
v
) + ( i
v
+ j
v
) = 7 i
v
7 j
v
u
v
+ 2 v
v
= (3 i
v
4 j
v
) + 2( i
v
+ j
v
) = 5 i
v
2 j
v
2 u
v
+ v
v
u
v
+ 2 v
v
θ
cos θ =
|j2i5||j7i7|
)j2i5()j7i7(
vvvv
vvvv
−−
−⋅−
=
2222
2577
)2)(7(57
++
−+×
=
2927
49
=
58
7
F cos 30° =
2
3
∴ cos θ ≠ cos 30°
∴ θ ≠ 30°
F 2 u
v
+ v
v
30° u
v
+ 2 v
v
F
F 1 ˈ
2. u
v
2 v
v
= (3 i
v
4 j
v
) 2( i
v
j
v
) = i
v
6 j
v
( u
v
2 v
v
)⋅(6 i
v
j
v
) = ( i
v
6 j
v
)⋅(6 i
v
j
v
)
= 6 × 1 + 1(-6) = 0
F F u
v
2 v
v
6 i
v
+ j
v
3. u
v
+ v
v
= 3 i
v
+ 4 j
v
+ i
v
+ j
v
= 4 i
v
3 j
v
F F F u
v
+ v
v
|vu|
)vu(
vv
vv
+
+
∴
|vu|
)vu(
vv
vv
+
+
=
|j3i4|
)j3i4(
vv
vv
−
−
=
22
34
)j3i4(
+
−
vv
=
5
4−
i
v
+
5
3
j
v
4. u
v
v
v
= (3 i
v
4 j
v
) ( i
v
+ j
v
) = 2 i
v
5 j
v
| u
v
v
v
| = | 2 i
v
+ 5 j
v
| =
22
52 + = 29
| u
v
+ v
v
| = | 4 i
v
3 j
v
| =
22
34 + = 25
∴ | u
v
v
v
| ≥ | u
v
+ v
v
|

9. 84
12. F 4 (fog) (
3
1
) = f(g(
3
1
))
= f(arcsin
3
2
+ 2 arcsin
3
1
)
= sin(arcsin
3
2
+ 2 arcsin
3
1
)
F arcsin
3
2
= A
∴ sin A =
3
2
F arcsin
3
1
= B
∴ sin B =
3
1
∴ sin(arcsin
3
2
+ 2 arcsin
3
1
) = sin(A + 2B)
= sin A cos 2B + cos A sin 2B
= sin A(1 2 sin2
B) + cos A × 2 sin Bcos B
= (
3
2
)(1 2(
3
1
)2
) + Asin1 2
− 2 sin B × Bsin1 2
−
= (
3
2
)(1 -
9
2
) +
2
3
2
1 




− ×
3
2
×
2
3
1
1 




−
= (
3
2
)(
9
7
) +
9
4
1− ×
3
2
×
9
1
1−
= (
3
2
)(
9
7
) +
3
5
×
3
2
×
3
8
=
27
14
+
27
402
=
27
10414+
=
27
2
(7 + 2 10 )
13. F 1 sine F
Asin
a
=
Bsin
b
=
Csin
c
= k
∴ a = Asink , b = Bsink , c = Csink
Asin =
k
a
, Bsin =
k
b
, Csin =
k
c
F )CsinBsinA)(sinCsinBsinA(sin −+++ = BsinAsin3

10. 85
)
k
c
k
b
k
a
)(
k
c
k
b
k
a
( −+++ =
k
b
k
a
3 ⋅⋅
)cba)(cba(
k
1
2 −+++ = )ab3(
k
1
2
∴ )cba)(cba( −+++ = 3ab
∴ C = 60°
Cos C =
2
1
14. F 3 F 1( ʾ 1 F )
4
A ˈ 2x + 3y = 100 ---------(1)
y x = 5 ----------(2)
F F x = 21 , y = 26
∴ A (21, 26)
B ˈ x + y = 10 .. (1) C x + y = 10 F y = 2
y x = 5 .. (2) ∴ C(8, 2)
B = )2
15,2
5( < > D 2x + 3y = 120 F y = 2
∴ D = (57, 2)
4 P
P = 3x + y
(21, 26) P = 89
)2
15,2
5( P = 15 → min
(8, 2) P = 26
(57, 2) P = 173 → max
A
D
B
C
2=y
(60,0)(10,0)
(0,10)
(0,40)
10=+ yx
12032 =+ yx
5=− yx
a = max = 173
b = min = 15
a b = 173 15 = 158
F 3

11. 86
15. F 3
F F . . F F
Z 1 = -1 - 3 i
= 2 





−− i
2
3
2
1
= 2 (cos 240°+ i sin 240°)
Z1
6
= 2
6
(cos 1440°+ i sin 1440°)
= 64 (cos 0°+ i sin 0°)
= 64
(z 2 )3
=
2
1
+
2
i3
= cos 60° + i sin 60°
(z2
3
)9
= cos (9 x 60°) + i sin (9 x 60°)
z2
27
= cos 540° + i sin 540°
z2
27
= cos (360° x 180°) + i sin (360° x 180°)
z2
27
= -1
Z1
6
+ (Z 2) 27
= 64 -1 = 63
16. F 1 z94iz 1
+−
= 26
z9
z
4i
+ = 26
z
z9z4i ⋅+
= 26
z
z9z4i ⋅+
= 26
2
z94i + = z26
222
)z(94 + = z26
4
z8116 + =
2
z72 2 F
16z72z81
24
+− = 0
22
4)z(9 − = 0
4z9
2
− = 0
2
z = 0
z =
3
2
17. F 4 4 8 F 





4
8
= 70
4 F F 0
ˈ F 4 1
∴ F ˈ =
70
1
( F )
0z,
z
1
z 1
≠=−
zzz =⋅
22
)F()F(z +=

12. 87
18. F 3 ( F F 4 )
F F F F ʾ !
P ( F ) = P( F 2) + P( F 2) + P( F 2)
=












+












+












2
12
2
5
2
12
2
4
2
12
2
3
=
66
10
66
6
66
3
++
=
66
19
19. F 1
20. F 3
)(lim
3
xf
x +
→
)(lim
3
axf
x −
→
f(3)






−
−
+
→ 33x
93x
lim
3x
F
0
0
∴ DIFF
3 x = 3
x32
3 6
= 6a)(axlim 2
3x
−−
→
= 6a9a −
= 3a
= 69a(3)2
−
= 6a9a −
= 3a
ˆ F F 3 F F
f(x) 6 = 3a = 3a
a = 2
F f(x) = 122x2
− , x ≤ 3
f′(x) = 4x , x ≤ 3
f′(a) = f′(2) = 8
21. F 1 F Calculus ˆ ˆ F fg,gf oo
f(x) = 13x +
)(xgf o = 1x2
+
F g(x) =
3
11)(x 22
−+
=
3
1
1)(x
3
1 22
−+
f′(x) + g′(x) = 1)(2x)(x
3
2
13x2
3 2
++
+
f′(1) + g′(1) =
3
8
4
3
+ =
12
41

13. 88
22. F 2
y = 104axxa 22
++
A = ∫ ++
1
0
22
10)dx4axx(a
= 1
0
2
3
2
10x)2ax
3
x
(a ++
= 102a
3
a2
++
∴ A = 102a
3
a2
++
F F A′ = 2
3
2a
+ = 0
2a = 6
a = 3
∴ F a = 3
A = 102(3)
3
(3)2
++ = 7
23. F 2
F F F
F f
46 55
56 65
66 75
76 85
86 95
96 105
4
x
y
10
7
3
4
4 + x
4 + x + y
14 + x + y
21 + x + y
24 + x + y
24 + x + y
1Q F (n)
4
1
= y)x(24
4
1
++
Med F (n)
2
1
= y)x(24
2
1
++
1Q = 65.5 56 65
∴ 4 + x = y)x(24
4
1
++ ..( )
16 + 4x = 24 + x + y
3x y = 8 (1)
Med = 75.5 66 75 ( )

14. 89
∴ 4 + x + y = y)x(24
2
1
++
8 + 2x + 2y = 24 + x + y
x + y = 16 (2)
F (1) (2) F x = 6, y = 10 ∴ N = 40
F 3Q F 30(40)
4
3
(N)
4
3
==
F 4 ( F F F )
∴ 3Q 3Q = 85.5
F F F
∴ Q.D. =
2
QQ 13 −
=
2
65.535.5 −
= 10
24. F 3 X = 70 , Mo = = 40
Med = = 60
1. F Q ∑ −
=
N
1i
X ≤ ∑ −
=
N
1i
aX a ˈ
= 60 ∴ ∑ −
=
100
1i
i 60X < ∑ −
=
100
1i
i 70X
2. F Q ( )∑ −
=
N
1i
2
XX ≤ ( )∑ −
=
N
1i
2
aX a ˈ
X = 70 ∴ ( )∑ −
=
100
1i
2
i 70X < ( )∑ −
=
100
1i
2
i 40X
3. Mo < Med < X
∴ ˈ F F F
4. F F F = 60
F F F F 60 50 F F60
25. F 3 F F F F F F F F F
Mo
40
Med
40
x
70
F x F F
36 60ix
z 2
12
6036
−=
−
0
=
63 x
ix
z 1
7
7063
−=
− 0
7.. =DS
70x

15. 90
F F F F F
60)xP(36 i << 0)z2P( <<−=
2)zP(0 <<= ( ʽ z . .) 0.477=
F 60)xP(36 i << 0)z2P( <<−=
2)zP(0 <<= ( ʽ z . .) 0.477=
F 60)xP(36 i << x)xP(36 i <<= F F F F 0.477 F F F x F
F F F F x F F )xxP(36 i << F F F F F F 0.477 F F
F F F x F x F F F 0.477 F F F F F x F x
F F F 0.477 F x F F x
0)z1P()xxP(63 i <<−=<<
1)zP(0 <<= 0.341=
F x F F x x F F
x)xP(63 i << 60)xP(36 i <<=
0.477x)xxP()xxP(63 ii =<<+<<
0.477)zzP(00.341 i =<<+
0.1360.3410.4770.35)zP(0 =−=<< ʽ z
∴ F x z F 0.35
SD
xx
z i −
=
7
70x
0.35
−
=
72.452.4570x =+=
2
1. F 3. 1800
2. F 4. 3
3. F 1. 2.09
4. F 2. 16
5. F 3. 1
6. F 4. 17
7. F 3. 4
8. F 1. 25
9. F 3. 0.2
10. F 2. 2.33