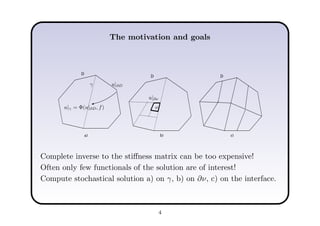
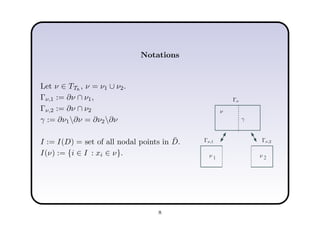
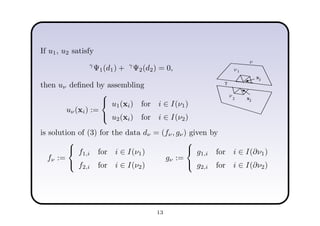
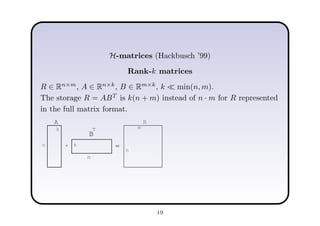
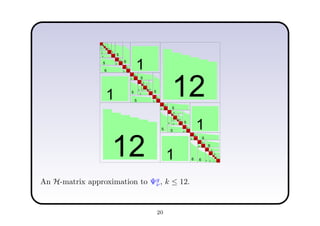
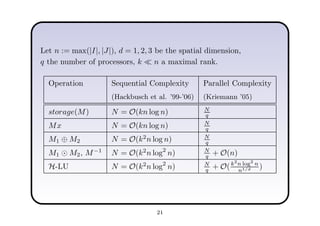
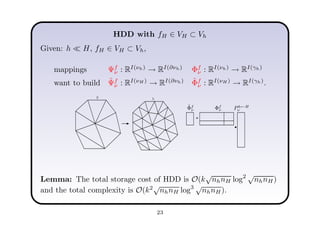
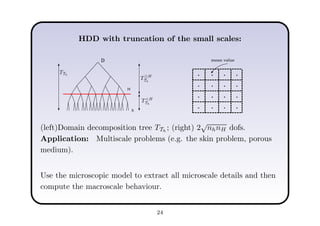
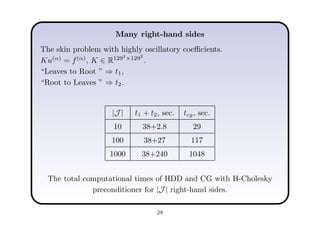
This document describes a hierarchical domain decomposition (HDD) method for solving stochastic elliptic boundary value problems with oscillatory or jumping coefficients. HDD constructs mappings between boundary and interface values that allow the solution to be computed locally in each subdomain. These mappings are represented as H-matrices to reduce computational costs. The total storage cost of HDD is O(kn log2nh) and complexity is O(k2nh log3nh), where n is the number of degrees of freedom, k is the H-matrix rank, and h is the mesh size. HDD can also be used to compute solutions when the right-hand side is represented on a coarser grid.

1. Application of H-matrices for solving
multiscale problems with stochastical right hand side
Litvinenko Alexander
WIRE, TU Braunschweig,
5 April, 2007.
www.hlib.org www.wire.tu-bs.de
1

2. Contents
1. Problem Setup
2. Hierarchical Domain Decomposition (HDD)
3. HDD in the H-matrix arithmetic
4. Computational resources of HDD
5. Functionals of the solution
6. Numerical results
2

3. Problem setup
The stochastic elliptic boundary value problem: find u : Ω × D → R
s.t. : almost surely



1≤i,j≤2
∂
∂xi
αi,j(x)
∂
∂xj
u = f(x, ω) on D
u = g(x, ω) in ∂D
(1)
where αi,j ∈ L∞
(D) such A(x) = (αi,j)i,j=1,2 satisfies
0 < λ ≤ λmin(A(x)) ≤ λmax(A(x)) ≤ λ , ∀x ∈ D.
⇒ Oscillatory or jumping coefficients are allowed.
3

4. The motivation and goals
a) b) c)
D
D D
u|∂Dγ
ν
u|∂ν
u|γ = Φ(u|∂D, f)
Complete inverse to the stiffness matrix can be too expensive!
Often only few functionals of the solution are of interest!
Compute stochastical solution a) on γ, b) on ∂ν, c) on the interface.
4

5. From H.Matthies and A.Keese Bericht Nr. 08-2003
K˜u(ω) = K
α∈J
u(α)
Hα(ω) =
α∈J
Ku(α)
Hα(ω) =
˜f(ω) =
α∈J
f(α)
Hα(ω).
where u(α)
can by find by solving uncoupled systems
∀α ∈ J : Ku(α)
= f(α)
.
How to compute all u(α)
efficiently? a) K−1
, b) LU and c) CG
(GMRES)?
5

6. The idea of HDD
Apply Galerkin FE discretisation to (1).
We construct the discrete solution in the form
uh(·, ω) = Fhfh(·, ω) + Ghgh(·, ω), (2)
where Fh, Gh are two solution operators, fh is the st. FE rhs and gh
is the st. FE Dirichlet-boundary values.
E.g. uh(fh, gh) only for fh in a coarser space.
6

7. Domain decomposition tree (TTh
)
FE discretisation: triangulation Th, D := Dh = ∪t∈Th
t.
1
2
3
4
5
6
7
9
10
11
12
13
14
15
8
5
6
7
11
12
13
14
15
8
1
2
3
4
5
6
7
9
10
3
4
1
9
10
......
5
6
11
12
13
14
15
6
7
11
15
8
......
2
6
2
6
• D is the root of the tree,
• TTh
is a binary tree,
• if ν ∈ TTh
has two sons ν1, ν2 ∈ TTh
:
ν = ν1 ∪ ν2
and γ = ∂ν1 ∩ ∂ν2,
• ν ∈ TTh
is a leaf, if and only if ν ∈ Th.
7

8. Notations
Let ν ∈ TTh
, ν = ν1 ∪ ν2.
Γν,1 := ∂ν ∩ ν1,
Γν,2 := ∂ν ∩ ν2
γ := ∂ν1∂ν = ∂ν2∂ν
I := I(D) = set of all nodal points in ¯D.
I(ν) := {i ∈ I : xi ∈ ν}.
1 2
γ
Γν,1 Γν,2
Γν
ν
νν
8

9. FE Galerkin Discretisation
For ν ∈ TTh
define fν := (fi)i∈I(ν), gν := (gi)i∈I(∂ν), dν := (fν, gν).
Let bj, j = 1, ..., N be a piecewise linear basis,
Vh := span{b1, ..., bN }, Vh ⊂ V = H1
(D).
Variational Galerkin formulation of (1): find uh ∈ Vh such that



aν(uh, bj) = (fν, bj)L2(ν) ∀ j ∈ I(
◦
ν),
uh(xj) = gj ∀ j ∈ I(∂ν),
(3)
where
aν(bi, bj) =
D
α(x)(∇bi, ∇bj)dx,
(fν, bj) =
suppbj
fνbjdx.
9

10. Let Uν ∈ Vh be the solution of (3), then Uν = Uf
ν + Ug
ν ,
where Uf
ν is the solution of



aν(Uf
ν , bj) = (fν, bj)L2(ν) , ∀ j ∈ I(
◦
ν),
Uf
ν (xj) = 0, ∀ j ∈ I(∂ν)
and Ug
ν is the solution of



aν(Ug
ν , bj) = 0, ∀ j ∈ I(
◦
ν),
Ug
ν (xj) = gj, ∀ j ∈ I(∂ν).
10

11. Main point of HDD is to build the mapping Φν := (Φg
ν, Φf
ν ), where
Φg
ν : RI(∂ν)
→ RI(γ)
and Φf
ν : RI(ν)
→ RI(γ)
for each ν ∈ TTh
.
1. Definition of Mapping Φν
(Φν(dν))i := uh(xi) , ∀i ∈ I(γ).
Hence, Φν(dν) is the trace of uh on γ.
Actually, Φνdν = Φg
νgν + Φf
ν fν.
2. Definition of auxiliary Mapping Ψν := (Ψg
ν, Ψf
ν )
Ψν(d) = (Ψν(dν))i∈I(∂ν) with (Ψν(dν))i := aν(uh, bi) − (fν, bi)L2(ν) ,
Ψνdν = Ψf
ν fν + Ψg
νgν.
11

12. Construction of the mappings Ψν and Φν
Lemma 1: Let ν1 and ν2 be two sons of ν ∈ TTh
. Let d1 and d2 be
the data associated to ν1 and ν2 s.t. :
• (consistency conditions for the Dirichlet data)
g1,i = g2,i , ∀i ∈ I(ν1) ∩ I(ν2),
• (consistency conditions for the right-hand side)
f1,i = f2,i , ∀i ∈ I(ν1) ∩ I(ν2).
1
2
xj
γ
xj
ν
ν
ν
Let u1 and u2 be the local FE solutions of the problem (3) for the
data d1, d2.
12

13. If u1, u2 satisfy
γ
Ψ1(d1) + γ
Ψ2(d2) = 0,
then uν defined by assembling
uν(xi) :=



u1(xi) for i ∈ I(ν1)
u2(xi) for i ∈ I(ν2)
1
2
xj
γ
xj
ν
ν
ν
is solution of (3) for the data dν = (fν, gν) given by
fν :=



f1,i for i ∈ I(ν1)
f2,i for i ∈ I(ν2)
gν :=



g1,i for i ∈ I(∂ν1)
g2,i for i ∈ I(∂ν2)
13

14. Construction of Φν
Given: d1 := dν1 = (f1, g1,Γ, g1,γ), where g1,Γ := (g1)i∈I(Γν,1),
g1,γ := (g1)i∈I(γ). Then
Ψ1d1 = Ψf
1 f1 + ΨΓ
1 g1,Γ + Ψγ
1 g1,γ,
Ψ2d2 = Ψf
2 f2 + ΨΓ
2 g2,Γ + Ψγ
2 g2,γ.
Restricting to I(γ) and summing
( γ
Ψγ
1 + γ
Ψγ
2 ) gγ = (−Ψf
1 f1 − ΨΓ
1 g1,Γ − Ψf
2 f2 − ΨΓ
2 g2,Γ)|γ.
We set
M := −( γ
Ψγ
1 + γ
Ψγ
2 ),
compute M−1
and solve for gγ:
gγ = M−1
(Ψf
1 f1 + ΨΓ
1 g1,Γ + Ψf
2 f2 + ΨΓ
2 g2,Γ)|γ.
14

15. HDD consists of two algorithms
I. Construction of Φν for all ν ∈ TTh
1. Compute Ψν for all leaves of TTh
(∈ R3×3
matrices).
2. Recursion from the leaves to the root (end if ν = D):
(a) Compute Ψν and Φν from Ψ1, Ψ2.
(b) Store Φν and delete Ψ1, Ψ2.
15

16. II. Application of Φν
1. Given dν = (fν, gν), compute the solution uh on the interface γ
by Φν(dν).
2. Build the data d1 = (fν1 , gν1 ), d2 = (fν2 , gν2 ) from dν = (fν, gν)
and gγ = Φν(dν).
3. Repeat for sons of ν1 and ν2.
16

17. HDD in the H-matrix arithmetic
The system of linear equations for ν ∈ TTh
is Au = Fc.
Rewrite it in the block matrix form:


ABB ABI
AIB AII




uB
uI

 =


FB
FI

 c,
where uB ∈ RI(∂ν)
, uI ∈ RI(γ)
, c ∈ RI(ν)
ABB ∈ RI(∂ν)
→ RI(∂ν)
, AII ∈ RI(γ)
→ RI(γ)
.
17

18. Eliminate uI:


ABB − ABIA−1
II AIB 0
AIB AII




uB
uI

 =


FB − ABIA−1
II FI
FI

 c.
(ABB − ABIA−1
II AIB)uB = (FB − ABIA−1
II FI)c
uI = A−1
II FIc − A−1
II AIBuB,
Ψg
ν :=ABB − ABIA−1
II AIB (Schur complement)
Ψf
ν :=FB − ABIA−1
II FI,
Φg
ν :=A−1
II AIB
Φf
ν :=A−1
II FI.
Exact HDD requires expensive matrix arithmetic.
Apply the H-matrix techniques.
18

19. H-matrices (Hackbusch ’99)
Rank-k matrices
R ∈ Rn×m
, A ∈ Rn×k
, B ∈ Rm×k
, k ≪ min(n, m).
The storage R = ABT
is k(n + m) instead of n · m for R represented
in the full matrix format.
=
A
B
T
*
R
k
k
n
m
n
m
19

20. 25 4
4 8
5
5 16 5
5 16
5
5 32 6
6 32
5
5
32 5
5 32
6
6
32 5
5 32
1
1
32 5
5 32 5
5
32 5
5
16 4
4 32 5
5 16
5
5 32
5
5
32 5
5 32
12
12
32 5
5 32 5
5
32 5
5
16 5
5
32 4
4 16
5
5 32
5
5
32 5
5 32
1
1
32 5
5 32 6
6
32 5
5 32 6
6
32 5
5
32 5
5
16 5
5
16 4
4 31
An H-matrix approximation to Ψg
ν, k ≤ 12.
20

21. Let n := max(|I|, |J|), d = 1, 2, 3 be the spatial dimension,
q the number of processors, k ≪ n a maximal rank.
Operation Sequential Complexity Parallel Complexity
(Hackbusch et al. ’99-’06) (Kriemann ’05)
storage(M) N = O(kn log n) N
q
Mx N = O(kn log n) N
q
M1 ⊕ M2 N = O(k2
n log n) N
q
M1 ⊙ M2, M−1
N = O(k2
n log2
n) N
q + O(n)
H-LU N = O(k2
n log2
n) N
q + O(k2
n log2
n
n1/d )
21

22. Computational resources for ν ∈ TTh
Lemma 2: Let ν ∈ TTh
, nν := |I(ν)| and
√
nν be the number of dofs
on the interface. Then the storage costs and computational
complexities of Ψg
ν, Ψf
ν , Φg
ν, Φf
ν are as shown in Table.
Storage Comput. complexity Application
Ψg
ν O(k
√
nν log
√
nν)∗
O(k2√
nν log2 √
nν) -
Ψf
ν O(knν log nν)∗
O(k2
nν log2
nν) -
Φg
ν O(k
√
nν) - O(k
√
nν)
Φf
ν O(knν log nν) - O(knν log nν)
Lemma 3: The total storage cost of HDD is O(kn log2
nh) and the
total complexity is O(k2
nh log3
nh).
22

23. HDD with fH ∈ VH ⊂ Vh
Given: h ≪ H, fH ∈ VH ⊂ Vh,
mappings Ψf
ν : RI(νh)
→ RI(∂νh)
Φf
ν : RI(νh)
→ RI(γh)
want to build ˜Ψf
ν : RI(νH )
→ RI(∂νh) ˜Φf
ν : RI(νH )
→ RI(γh)
.
H h
.
=
Φf
ν
˜Φf
ν Ph←H
ν
Lemma: The total storage cost of HDD is O(k
√
nhnH log2 √
nhnH)
and the total complexity is O(k2√
nhnH log3 √
nhnH ).
23

24. HDD with truncation of the small scales:
D
h
H
T≥H
Th
TTh
T<H
Th
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
mean value
(left)Domain decomposition tree TTh
; (right) 2
√
nhnH dofs.
Application: Multiscale problems (e.g. the skin problem, porous
medium).
Use the microscopic model to extract all microscale details and then
compute the macroscale behaviour.
24

25. Truncation of the scales < H
Memory costs of all Φg
ν (in kB). Maximal rank is k = 7.
dofs Φg
, H = h Φg
, H = 0.125
332
2.45 ∗ 102
2 ∗ 102
652
1.1 ∗ 103
7.9 ∗ 102
1292
5 ∗ 103
2.6 ∗ 103
2572
2.1 ∗ 104
7.4 ∗ 103
25

26. Memory costs of all Φf
ν (in kB). Maximal rank is k = 7.
dofs Φf
, H = h Φf
, H = 0.125
332
4 ∗ 102
2.8 ∗ 102
652
2.4 ∗ 103
1.8 ∗ 103
1292
1.4 ∗ 104
1.2 ∗ 104
2572
7.9 ∗ 104
6.9 ∗ 104
26

27. The mean value of the solution in ν
Lemma 4: Let ν, ν1, ν2 ∈ TTh
and ν = ν1 ∪ ν2. Let
λνi (dνi ) = (λg
νi
, gνi ) + (λf
νi
, fνi ) computes the mean value in νi,
i = 1, 2. Then
λν(dν) = (λf
ν , fν) + (λg
ν, gν)
computes the mean value in ν. Here
λf
ν : RI(ν)
→ R, fν ∈ RI(ν)
,
λg
ν : RI(∂ν)
→ R, gν ∈ RI(∂ν)
,
λf
ν = c1λf
ν1
+ c2λf
ν2
,
λg
ν = c1λg
ν1
+ c2λg
ν2
,
gν is built from gν1 , gν2 and g|γ := Φν(dν).
27

28. Many right-hand sides
The skin problem with highly oscillatory coefficients.
Ku(α)
= f(α)
, K ∈ R1292
×1292
.
“Leaves to Root ” ⇒ t1,
“Root to Leaves ” ⇒ t2.
|J | t1 + t2, sec. tcg, sec.
10 38+2.8 29
100 38+27 117
1000 38+240 1048
The total computational times of HDD and CG with H-Cholesky
preconditioner for |J | right-hand sides.
28

29. Conclusion:
1. HDD computes Fh, Gh and uh(·, ω) = Fhfh(·, ω) + Ghgh(·, ω).
2. Fh and Gh are successfully approximated in the H-matrix format.
3. The storage requirement is O(knh log2
nh).
4. The complexity is O(k2
|J |nh log3
nh).
5. HDD allows to compute functionals of the solution.
6. HDD is well parallelizable with a small data exchange.
29

30. To do:
1)



1≤i,j≤2
∂
∂xi
αi,j(x, ω)
∂
∂xj
u = f(x, ω) x ∈ D, ω ∈ Ω,
u = g(x, ω) x ∈ ∂D, ω ∈ Ω,
and would like to get
u =
γ
∆γ
⊗ Bγ
f +


β
Λβ
⊗ Cβ

 g,
where ∆γ
, Λβ
is a stochastic part and Bγ
, Cβ
is a deterministic part.
2) functionals of the solution u for nonlinear problems.
30

31. Thanks for your attention!
Questions ?
31

32. 32