The document presents methods for modeling large networks using multifractal network generators (MFNG), focusing on scalability and estimation. It outlines a theoretical framework that allows for efficient graph generation and parameter fitting through method of moments estimation, demonstrating effectiveness with empirical data from synthetic and real-world networks. The authors also discuss challenges and solutions for fast sampling and estimating network structures.

1. Learning Multifractal Structure in Large Networks
Austin Benson, Carlos Riquelme, Sven Schmit
Stanford University
f arbenson, rikel, schmit g @ stanford.edu
Knowledge Discovery and Data Mining (KDD)
August 26, 2014

2. Setting
We want a simple, scalable method to model networks and generate
random (undirected) graphs
I Looking for graph generators that can mimic real world graph
structure
{ Power law degree distribution,
{ High clustering coecient, etc.
I Many models have been proposed, starting with Erdos-Renyi graphs
I Relatively recent models: SKG [Leskovec et al. 2010], BTER
[Seshadhri et al. 2012], TCL [Pfeier et al. 2012]
I In 2011 Palla et al. introduce multifractal network generators,
`generalizing' SKG
2

3. Our contributions
We propose methods to make MFNG a feasible framework to model large
networks
3

4. Our contributions
We propose methods to make MFNG a feasible framework to model large
networks
I First, we give an intuitive theoretical result that opens the door to
scalable estimation
I We show how we can

5. t MFNG to graphs using mehod of moments
estimation, with runtime independent of the size of the graph
I We develop a fast heuristic for sampling MFNG
I We demonstrate the ectiveness of our approach in synthetic and
real world settings.
3

6. An introduction to Multifractal Network Generators
(MFNG)
Ingredients
I Number of nodes: n
I Number of categories: m with speci

7. ed lenghts li
I Number of recursive levels: k logm(n)
I Probabilities of edges between nodes, based on categories, stored in
matrix P 2 [0; 1]mm
4

8. Generating a graph with no recursion
Let's consider the simple case

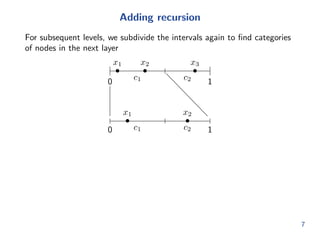
9. rst: k = 1
I Begin with a line: [0; 1]
I Divide the line in m intervals (or categories) with lengths
l1; l2; : : : ; lm
I Sample nodes on the line according to a uniform distribution: this
gives every node a category
x2
x3
c1 c2
x1
0 1
5

10. From line to square
c1 c2
x3
c2
x2
c1
x1
x2
x3
x1
pc1;c1
pc2;c2
pc1;c2
pc1;c2
I For any two nodes u 2 ci; v 2 cj , add an edge with probability
according to pci;cj
6

11. Adding recursion
For subsequent levels, we subdivide the intervals again to

12. nd categories
of nodes in the next layer
x2
x3
c1 c2
x1
0 1
x1
x2
0 c1 c2 1
7

13. Adding recursion
For subsequent levels, we subdivide the intervals again to

14. nd categories
of nodes in the next layer
x2
x3
c1 c2
x1
0 1
x1
x2
0 c1 c2 1
Now add an edge between nodes by multiplying probabilities
corresponding to categories in each layer.
In the above two layer example
I node x1 has categories (c1; c1),
I node x2 has categories (c1; c2), and
I node x3 has categories (c2; c2)
And hence, we add edge (x1; x2) with probability pc1;c1pc1;c2 .
7

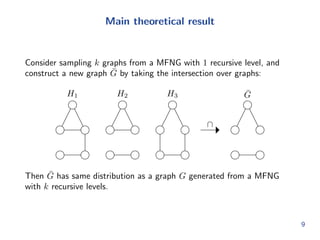
15. Expanding the recursion
So we can get a full probabilistic adjacency matrix Q 2 [0; 1]mkmk
by
expanding all recursive levels
Problem: Q grows fast with k. Dicult to do inference.
Intuitively, we should not have to do this.
8

16. Main theoretical result
Consider sampling k graphs from a MFNG with 1 recursive level, and
construct a new graph G
by taking the intersection over graphs:
H1 H2 H3 G
Then G
has same distribution as a graph G generated from a MFNG
with k recursive levels.
9

17. Computing expected number of edges is easy
p11 p12
p22
xi
xj
p13
p23
p33
`1 `2 `3
Prob((u; v) 2 E) = p =
X3
i=1
X3
j=1
`i`jpij ; E fjEjg =
n
2
pk
So computing p is O(m2) instead of O(m2k).
10

18. Computing moments of certain subgraphs is easy
With above theory, we can easily compute the expected number of...
I edges, wedges, 3-stars, 4-stars ...
I triangles, 4-cliques...
S2 S3 S4 K3 K4
11

19. We can learn multifractal structure quickly
Method of moments:
1. Count number of wedges, 3-stars, triangles, 4-cliques, etc. in
network of interest
2. Try to

20. nd parameters such that the expected values, E[Fi], match
the empirical counts, fi
minimize
P;`;r
X
i
jfi E[Fi]j
fi
subject to 0 pij = pji 1; 1 i j c
0 `i 1; 1 i c
Xm
i=1
`i = 1
Key idea: Once we have the counts (fi), this optimization routine is
independent of the size of the graph.
12