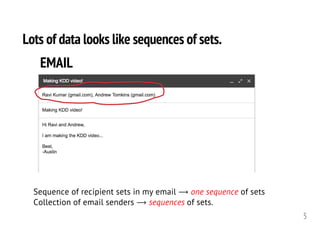
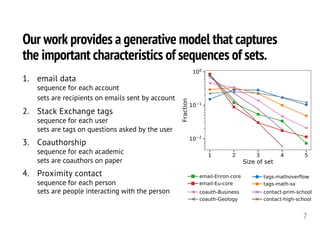
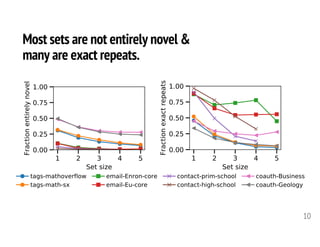
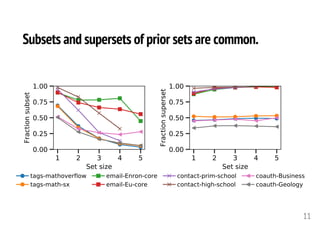
The document discusses three perspectives on predicting sets of items rather than single items. It describes how sets are common in data such as team formations, medical codes, and online purchases. It then discusses three specific approaches to set prediction: (1) predicting which sets an individual will interact with based on their history, (2) modeling sequences of sets using a generative model, and (3) understanding characteristics of set-based data like subsets and repeats. Applications include prediction, analysis, and simulation.

1. 1
Joint work with
Ravi Kumar & Andrew Tomkins (Google)
Rediet Abebe & Jon Kleinberg (Cornell)
Michael Schaub & Ali Jadbabaie (MIT)
Set prediction three ways
Austin R. Benson · Cornell
SCAN Seminar · September 10, 2018
Slides. bit.ly/arb-SCAN18

2. We usually think about predicting single-item events.
2

3. This talk looks at predicting sets from three perspectives.
3
Set-based data is common, but we don’t have a great understanding
of its complexities and the associated human behavior.
• Team formation (writing papers, organizational behavior).
• Multiple classification codes in hospital visits.
• Co-purchasing sets on Amazon.
• Sets of annotations on questions on web forums.

4. 4
Set Prediction #1. Individuals repeating interactions.
Given a history of an individual’s set-based interactions, which ones repeat?
Who will repeat as my coauthors on my next paper?
Sequences of Sets. Benson, Kumar, & Tomkins. KDD, 2018.

5. Lots of data looks like sequences of sets.
5
EMAIL
Sequence of recipient sets in my email ⟶ one sequence of sets
Collection of email senders ⟶ sequences of sets.

6. Lots of data looks like sequences of sets.
6
Q&A
FORUM
TAGS

7. Our work provides a generative model that captures
the important characteristics of sequences of sets.
7
1. email data
sequence for each account
sets are recipients on emails sent by account
2. Stack Exchange tags
sequence for each user
sets are tags on questions asked by the user
3. Coauthorship
sequence for each academic
sets are coauthors on paper
4. Proximity contact
sequence for each person
sets are people interacting with the person
tags-mathoverflow
tags-math-sx
email-Enron-core
email-Eu-core
contact-prim-school
contact-high-school
coauth-Business
coauth-Geology

8. Our work provides a generative model that captures
the important characteristics of sequences of sets.
8
Applications.
1. Predicting new sets.
2. Understanding basic user behaviors.
3. Generative model ⟶ event likelihood ⟶ anomaly detection.
4. Generative model ⟶ simulation.
5. Amenable to analysis.

9. 9
What are the important
characteristics of the data?

10. Most sets are not entirely novel &
many are exact repeats.
10
tags-mathoverflow
tags-math-sx
email-Enron-core
email-Eu-core
contact-prim-school
contact-high-school
coauth-Business
coauth-Geology

11. Subsets and supersets of prior sets are common.
11
tags-mathoverflow
tags-math-sx
email-Enron-core
email-Eu-core
contact-prim-school
contact-high-school
coauth-Business
coauth-Geology

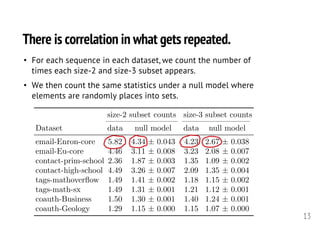
12. There is recency bias in the repeat behavior.
12
Consistent with previous results on sequences of single items.
[Benson-Kumar-Tomkins 16; Anderson+ 14]

13. size-2 subset counts size-3 subset counts
Dataset data null model data null model
email-Enron-core 5.82 4.34 ± 0.043 4.23 2.67 ± 0.038
email-Eu-core 4.46 3.11 ± 0.008 3.23 2.08 ± 0.007
contact-prim-school 2.36 1.87 ± 0.003 1.35 1.09 ± 0.002
contact-high-school 4.49 3.26 ± 0.007 2.09 1.35 ± 0.004
tags-mathoverflow 1.49 1.41 ± 0.002 1.18 1.15 ± 0.002
tags-math-sx 1.49 1.31 ± 0.001 1.21 1.12 ± 0.001
coauth-Business 1.50 1.30 ± 0.001 1.40 1.24 ± 0.001
coauth-Geology 1.29 1.15 ± 0.000 1.15 1.07 ± 0.000
<latexit sha1_base64="PbRgN8ZetYi3/8RQh4MqDOE3dR8=">AAAHBXicdVXJjts2GFbS2E3UbdIceyE6bpAeZGjzjOcWpC3aYwp0kgCWMaBo2haGiyCSzUwFnXPuNX2G3ope+xx9hL5Ff1JepLFjwyD9bT9N/pTzkhVKh+G/9+5/9GAw/PjhI/+TTz/7/IuTx1++UtJUhF4SyWT1JseKskLQS11oRt+UFcU8Z/R1fv2d5V//SitVSPGLvi3pnOOVKJYFwRqgq8eDB5mgb4nkHItFnS2whjDdzKJ5nWl6o4WsOGb1adQ0fk9JRSVFs3PUlOOCBT9YNCCyogd6cyg2R5VECl1WBe/oLYSJDiwcKLKWkh1zrYvV+ojLwh9wcazX6qbj0XilAosGAB8RS9jMJZNvj1l23B1fbhScjlK9pWEDNV5smTuOFYWDW90eGn7cEI3vZzldFQKqw1E3M53P/QyEjIqVXsPZ4RyaQ9GyqeNSNx21YbhqaoZI+wZKy7IyjPpPUcYN0wUYDRd13NSkqVXxGw1ipEwO6YhII7TKyjUWWvIatgg9RR+0JX1bg7LMzwgvFrbcs+rbOg6SpgekwaTxv29/MyTbXw+DMIwhLheUHcWyDPnZJsQftZ05AslkPI1hSMdJikZZyUcoHIdp4qDYDvH47HzPJFNYHtjNyCnSMxiScRTtFeHUQRsvfNsz58iZt707corERkTjaadImDgombghvOgwMdpn2Ja1GXYdF23Rs141t4CLbdaeSduMbjuOnCptxWnUq2ihaNoOkx6zi1E3vYCkGxA5KG6HKO4yzr/t/DZhErYJ4UFC2jJx2mNcxOYqtAnxxeFSwy3kNvS8x9h+y6WGVnW9Aa2x2F2B3Te4Plcnp85gPYeTaDM59Tavl1cn/2ULSQynQhOGlZpFYannNa7gGkCenxm4ephc4xWdwVRgTtW8do/rBn0DyAItZQUfYS8HoF1HjblStzwHpTuAu5wFj3Ezo5fTeV2I0mgqSFtoaRjSEtlnP1oUFSWa3cIEk6qAtSKyxhU8I+Efolcll/IatkbBcwb2Jrq7E4eTV/E4CsfRz/Hp8xebXXrofeV97T3zIu/ce+795L30Lj0yuB78Png/+GP4bvjn8K/h3630/r2N54nXew3/+R80STIk</latexit><latexit sha1_base64="PbRgN8ZetYi3/8RQh4MqDOE3dR8=">AAAHBXicdVXJjts2GFbS2E3UbdIceyE6bpAeZGjzjOcWpC3aYwp0kgCWMaBo2haGiyCSzUwFnXPuNX2G3ope+xx9hL5Ff1JepLFjwyD9bT9N/pTzkhVKh+G/9+5/9GAw/PjhI/+TTz/7/IuTx1++UtJUhF4SyWT1JseKskLQS11oRt+UFcU8Z/R1fv2d5V//SitVSPGLvi3pnOOVKJYFwRqgq8eDB5mgb4nkHItFnS2whjDdzKJ5nWl6o4WsOGb1adQ0fk9JRSVFs3PUlOOCBT9YNCCyogd6cyg2R5VECl1WBe/oLYSJDiwcKLKWkh1zrYvV+ojLwh9wcazX6qbj0XilAosGAB8RS9jMJZNvj1l23B1fbhScjlK9pWEDNV5smTuOFYWDW90eGn7cEI3vZzldFQKqw1E3M53P/QyEjIqVXsPZ4RyaQ9GyqeNSNx21YbhqaoZI+wZKy7IyjPpPUcYN0wUYDRd13NSkqVXxGw1ipEwO6YhII7TKyjUWWvIatgg9RR+0JX1bg7LMzwgvFrbcs+rbOg6SpgekwaTxv29/MyTbXw+DMIwhLheUHcWyDPnZJsQftZ05AslkPI1hSMdJikZZyUcoHIdp4qDYDvH47HzPJFNYHtjNyCnSMxiScRTtFeHUQRsvfNsz58iZt707corERkTjaadImDgombghvOgwMdpn2Ja1GXYdF23Rs141t4CLbdaeSduMbjuOnCptxWnUq2ihaNoOkx6zi1E3vYCkGxA5KG6HKO4yzr/t/DZhErYJ4UFC2jJx2mNcxOYqtAnxxeFSwy3kNvS8x9h+y6WGVnW9Aa2x2F2B3Te4Plcnp85gPYeTaDM59Tavl1cn/2ULSQynQhOGlZpFYannNa7gGkCenxm4ephc4xWdwVRgTtW8do/rBn0DyAItZQUfYS8HoF1HjblStzwHpTuAu5wFj3Ezo5fTeV2I0mgqSFtoaRjSEtlnP1oUFSWa3cIEk6qAtSKyxhU8I+Efolcll/IatkbBcwb2Jrq7E4eTV/E4CsfRz/Hp8xebXXrofeV97T3zIu/ce+795L30Lj0yuB78Png/+GP4bvjn8K/h3630/r2N54nXew3/+R80STIk</latexit><latexit sha1_base64="PbRgN8ZetYi3/8RQh4MqDOE3dR8=">AAAHBXicdVXJjts2GFbS2E3UbdIceyE6bpAeZGjzjOcWpC3aYwp0kgCWMaBo2haGiyCSzUwFnXPuNX2G3ope+xx9hL5Ff1JepLFjwyD9bT9N/pTzkhVKh+G/9+5/9GAw/PjhI/+TTz/7/IuTx1++UtJUhF4SyWT1JseKskLQS11oRt+UFcU8Z/R1fv2d5V//SitVSPGLvi3pnOOVKJYFwRqgq8eDB5mgb4nkHItFnS2whjDdzKJ5nWl6o4WsOGb1adQ0fk9JRSVFs3PUlOOCBT9YNCCyogd6cyg2R5VECl1WBe/oLYSJDiwcKLKWkh1zrYvV+ojLwh9wcazX6qbj0XilAosGAB8RS9jMJZNvj1l23B1fbhScjlK9pWEDNV5smTuOFYWDW90eGn7cEI3vZzldFQKqw1E3M53P/QyEjIqVXsPZ4RyaQ9GyqeNSNx21YbhqaoZI+wZKy7IyjPpPUcYN0wUYDRd13NSkqVXxGw1ipEwO6YhII7TKyjUWWvIatgg9RR+0JX1bg7LMzwgvFrbcs+rbOg6SpgekwaTxv29/MyTbXw+DMIwhLheUHcWyDPnZJsQftZ05AslkPI1hSMdJikZZyUcoHIdp4qDYDvH47HzPJFNYHtjNyCnSMxiScRTtFeHUQRsvfNsz58iZt707corERkTjaadImDgombghvOgwMdpn2Ja1GXYdF23Rs141t4CLbdaeSduMbjuOnCptxWnUq2ihaNoOkx6zi1E3vYCkGxA5KG6HKO4yzr/t/DZhErYJ4UFC2jJx2mNcxOYqtAnxxeFSwy3kNvS8x9h+y6WGVnW9Aa2x2F2B3Te4Plcnp85gPYeTaDM59Tavl1cn/2ULSQynQhOGlZpFYannNa7gGkCenxm4ephc4xWdwVRgTtW8do/rBn0DyAItZQUfYS8HoF1HjblStzwHpTuAu5wFj3Ezo5fTeV2I0mgqSFtoaRjSEtlnP1oUFSWa3cIEk6qAtSKyxhU8I+Efolcll/IatkbBcwb2Jrq7E4eTV/E4CsfRz/Hp8xebXXrofeV97T3zIu/ce+795L30Lj0yuB78Png/+GP4bvjn8K/h3630/r2N54nXew3/+R80STIk</latexit><latexit sha1_base64="PbRgN8ZetYi3/8RQh4MqDOE3dR8=">AAAHBXicdVXJjts2GFbS2E3UbdIceyE6bpAeZGjzjOcWpC3aYwp0kgCWMaBo2haGiyCSzUwFnXPuNX2G3ope+xx9hL5Ff1JepLFjwyD9bT9N/pTzkhVKh+G/9+5/9GAw/PjhI/+TTz/7/IuTx1++UtJUhF4SyWT1JseKskLQS11oRt+UFcU8Z/R1fv2d5V//SitVSPGLvi3pnOOVKJYFwRqgq8eDB5mgb4nkHItFnS2whjDdzKJ5nWl6o4WsOGb1adQ0fk9JRSVFs3PUlOOCBT9YNCCyogd6cyg2R5VECl1WBe/oLYSJDiwcKLKWkh1zrYvV+ojLwh9wcazX6qbj0XilAosGAB8RS9jMJZNvj1l23B1fbhScjlK9pWEDNV5smTuOFYWDW90eGn7cEI3vZzldFQKqw1E3M53P/QyEjIqVXsPZ4RyaQ9GyqeNSNx21YbhqaoZI+wZKy7IyjPpPUcYN0wUYDRd13NSkqVXxGw1ipEwO6YhII7TKyjUWWvIatgg9RR+0JX1bg7LMzwgvFrbcs+rbOg6SpgekwaTxv29/MyTbXw+DMIwhLheUHcWyDPnZJsQftZ05AslkPI1hSMdJikZZyUcoHIdp4qDYDvH47HzPJFNYHtjNyCnSMxiScRTtFeHUQRsvfNsz58iZt707corERkTjaadImDgombghvOgwMdpn2Ja1GXYdF23Rs141t4CLbdaeSduMbjuOnCptxWnUq2ihaNoOkx6zi1E3vYCkGxA5KG6HKO4yzr/t/DZhErYJ4UFC2jJx2mNcxOYqtAnxxeFSwy3kNvS8x9h+y6WGVnW9Aa2x2F2B3Te4Plcnp85gPYeTaDM59Tavl1cn/2ULSQynQhOGlZpFYannNa7gGkCenxm4ephc4xWdwVRgTtW8do/rBn0DyAItZQUfYS8HoF1HjblStzwHpTuAu5wFj3Ezo5fTeV2I0mgqSFtoaRjSEtlnP1oUFSWa3cIEk6qAtSKyxhU8I+Efolcll/IatkbBcwb2Jrq7E4eTV/E4CsfRz/Hp8xebXXrofeV97T3zIu/ce+795L30Lj0yuB78Png/+GP4bvjn8K/h3630/r2N54nXew3/+R80STIk</latexit>
There is correlation in what gets repeated.
13
• For each sequence in each dataset, we count the number of
times each size-2 and size-3 subset appears.
• We then count the same statistics under a null model where
elements are randomly places into sets.

14. 14
How do we model the next set in a
sequence given the history?

15. Our Correlated Repeat Unions (CRU) model captures
repeat behavior,recency bias,and correlations.
15
Setup.
Observe sequence of sets S1, …, Sk.
Given number r of repeated elements in Sk+1.
Model selects r elements from .
CRU model.
Start with , given r.
1. Sample set Sk-j from j steps back with recency weight wj.
2. Sample T by keeping each item x in Sk-j with correlation probability p.
3. .
4. Repeat steps 1—3 until .
(if T makes N too large, randomly drop elements from T)
[k
j=1Sj<latexit sha1_base64="JMq9QvYWP/n1zUVVfzVZ7XzazRU=">AAAHPnicfVVdb9s2FFW7zeu0r3R53Au71MBQ2I6VIksyIICBFcUKtFg2O22ByM0o6spiTVIaSTV2Cf2WvW7/Yn9jf2Bvw173uEvbWSwnGwFbFHnPObyXR2RSCm5sv//7rdvvvPte6/07H4QffvTxJ59u3f3suSkqzeCUFaLQLxNqQHAFp5ZbAS9LDVQmAl4k02/8/Is3oA0v1MjOSxhLOlE844xaHDrf2r4fs6o8d6+Po/qVm9bD89f3z7d2+r3+opHrnWjV2QlW7eT8bms7TgtWSVCWCWrMWdQv7dhRbTkTUIdxZaCkbEoncIZdRSWYsVusviZtHElJVmj8KUsWo+E6BHk0nTdYnKVJJaieNUeTopjijKnDsKlps8Ox46qsLCi2lMwqQWxBfFFIyjUwK+akqWv59G1HcQaZpqxDpZHU5p2S+3V27PRtd6JpmXcknQIDIa6GlqvycMETTfXcp1BcmE6CzBNdVCo1nZJaC1oZxFvNZx2T0xJMJ+O2w6hg/j31mFIUVlI9Nf/F2pNgKU4uKifAulGVWfgB0tppSO8d9u8lAnXXI2wOEw2gard4+JiLnFvYiElEBbXz/2sRYZvk1pbm691dC7OescgNM5ZTNYEeK+TuTxUY7y6zG321f7R3tGtAcjRhgp6T3Qtu865PostVN0Grgl7EPTzYWT7C2BeUopV9fcJ4IoqEihhfYw8bgDKVhkFaCDTAAI3MihSOYw2Czi6xBS6+aaKzUTR2fuO8ARq7fDIaUuWLq0HBBSYgqUpdnFHJxTyFjFbC1i422WW/aRKTeVfUYXtdzOAOQnrc7x11mOQoirYQaHkUsDOTeYpmksgdKzvzVIMl2JkHZ/it7Y/rzaQeAX5kGoZzmRTiMabkliymdt89e1o75SUkr52sHcflxkOwNwXjQLoJSVaQlYYHDKsEt9NWfktvFthUGD5+5ktyKTCKGuVzyax2RlyJ+OAl2j3BSF8DKsqc1ldL/fHJRtXTiQDO8u6y9jfN4EYbPF6a54P0NOu7LId8IlEpXrrK07k4kS5ejtfXbCGf4uGa3oRYTdRNiQfxLKH6DM0X50kxc/Eb/98O41xXAkgOfJJbPF0P9ktL2mSUA6HMVlQQhIXxFE+Ifm9vH2Ztctna5BFeDFQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBt9+LQLYv0cO80FgdriakUARNRQRklhiegkes5bUT1f+S4AXw8H9J9CKTBUvtq4DXSLR5aVzvPN/rRbi87/d2BoerC+VO8HnwRfBlEAUHwSD4NjgJTgMWzIOfg1+CX1u/tf5o/dn6axl6+9YKsx00WuvvfwAkCY0R</latexit><latexit sha1_base64="JMq9QvYWP/n1zUVVfzVZ7XzazRU=">AAAHPnicfVVdb9s2FFW7zeu0r3R53Au71MBQ2I6VIksyIICBFcUKtFg2O22ByM0o6spiTVIaSTV2Cf2WvW7/Yn9jf2Bvw173uEvbWSwnGwFbFHnPObyXR2RSCm5sv//7rdvvvPte6/07H4QffvTxJ59u3f3suSkqzeCUFaLQLxNqQHAFp5ZbAS9LDVQmAl4k02/8/Is3oA0v1MjOSxhLOlE844xaHDrf2r4fs6o8d6+Po/qVm9bD89f3z7d2+r3+opHrnWjV2QlW7eT8bms7TgtWSVCWCWrMWdQv7dhRbTkTUIdxZaCkbEoncIZdRSWYsVusviZtHElJVmj8KUsWo+E6BHk0nTdYnKVJJaieNUeTopjijKnDsKlps8Ox46qsLCi2lMwqQWxBfFFIyjUwK+akqWv59G1HcQaZpqxDpZHU5p2S+3V27PRtd6JpmXcknQIDIa6GlqvycMETTfXcp1BcmE6CzBNdVCo1nZJaC1oZxFvNZx2T0xJMJ+O2w6hg/j31mFIUVlI9Nf/F2pNgKU4uKifAulGVWfgB0tppSO8d9u8lAnXXI2wOEw2gard4+JiLnFvYiElEBbXz/2sRYZvk1pbm691dC7OescgNM5ZTNYEeK+TuTxUY7y6zG321f7R3tGtAcjRhgp6T3Qtu865PostVN0Grgl7EPTzYWT7C2BeUopV9fcJ4IoqEihhfYw8bgDKVhkFaCDTAAI3MihSOYw2Czi6xBS6+aaKzUTR2fuO8ARq7fDIaUuWLq0HBBSYgqUpdnFHJxTyFjFbC1i422WW/aRKTeVfUYXtdzOAOQnrc7x11mOQoirYQaHkUsDOTeYpmksgdKzvzVIMl2JkHZ/it7Y/rzaQeAX5kGoZzmRTiMabkliymdt89e1o75SUkr52sHcflxkOwNwXjQLoJSVaQlYYHDKsEt9NWfktvFthUGD5+5ktyKTCKGuVzyax2RlyJ+OAl2j3BSF8DKsqc1ldL/fHJRtXTiQDO8u6y9jfN4EYbPF6a54P0NOu7LId8IlEpXrrK07k4kS5ejtfXbCGf4uGa3oRYTdRNiQfxLKH6DM0X50kxc/Eb/98O41xXAkgOfJJbPF0P9ktL2mSUA6HMVlQQhIXxFE+Ifm9vH2Ztctna5BFeDFQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBt9+LQLYv0cO80FgdriakUARNRQRklhiegkes5bUT1f+S4AXw8H9J9CKTBUvtq4DXSLR5aVzvPN/rRbi87/d2BoerC+VO8HnwRfBlEAUHwSD4NjgJTgMWzIOfg1+CX1u/tf5o/dn6axl6+9YKsx00WuvvfwAkCY0R</latexit><latexit sha1_base64="JMq9QvYWP/n1zUVVfzVZ7XzazRU=">AAAHPnicfVVdb9s2FFW7zeu0r3R53Au71MBQ2I6VIksyIICBFcUKtFg2O22ByM0o6spiTVIaSTV2Cf2WvW7/Yn9jf2Bvw173uEvbWSwnGwFbFHnPObyXR2RSCm5sv//7rdvvvPte6/07H4QffvTxJ59u3f3suSkqzeCUFaLQLxNqQHAFp5ZbAS9LDVQmAl4k02/8/Is3oA0v1MjOSxhLOlE844xaHDrf2r4fs6o8d6+Po/qVm9bD89f3z7d2+r3+opHrnWjV2QlW7eT8bms7TgtWSVCWCWrMWdQv7dhRbTkTUIdxZaCkbEoncIZdRSWYsVusviZtHElJVmj8KUsWo+E6BHk0nTdYnKVJJaieNUeTopjijKnDsKlps8Ox46qsLCi2lMwqQWxBfFFIyjUwK+akqWv59G1HcQaZpqxDpZHU5p2S+3V27PRtd6JpmXcknQIDIa6GlqvycMETTfXcp1BcmE6CzBNdVCo1nZJaC1oZxFvNZx2T0xJMJ+O2w6hg/j31mFIUVlI9Nf/F2pNgKU4uKifAulGVWfgB0tppSO8d9u8lAnXXI2wOEw2gard4+JiLnFvYiElEBbXz/2sRYZvk1pbm691dC7OescgNM5ZTNYEeK+TuTxUY7y6zG321f7R3tGtAcjRhgp6T3Qtu865PostVN0Grgl7EPTzYWT7C2BeUopV9fcJ4IoqEihhfYw8bgDKVhkFaCDTAAI3MihSOYw2Czi6xBS6+aaKzUTR2fuO8ARq7fDIaUuWLq0HBBSYgqUpdnFHJxTyFjFbC1i422WW/aRKTeVfUYXtdzOAOQnrc7x11mOQoirYQaHkUsDOTeYpmksgdKzvzVIMl2JkHZ/it7Y/rzaQeAX5kGoZzmRTiMabkliymdt89e1o75SUkr52sHcflxkOwNwXjQLoJSVaQlYYHDKsEt9NWfktvFthUGD5+5ktyKTCKGuVzyax2RlyJ+OAl2j3BSF8DKsqc1ldL/fHJRtXTiQDO8u6y9jfN4EYbPF6a54P0NOu7LId8IlEpXrrK07k4kS5ejtfXbCGf4uGa3oRYTdRNiQfxLKH6DM0X50kxc/Eb/98O41xXAkgOfJJbPF0P9ktL2mSUA6HMVlQQhIXxFE+Ifm9vH2Ztctna5BFeDFQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBt9+LQLYv0cO80FgdriakUARNRQRklhiegkes5bUT1f+S4AXw8H9J9CKTBUvtq4DXSLR5aVzvPN/rRbi87/d2BoerC+VO8HnwRfBlEAUHwSD4NjgJTgMWzIOfg1+CX1u/tf5o/dn6axl6+9YKsx00WuvvfwAkCY0R</latexit><latexit sha1_base64="JMq9QvYWP/n1zUVVfzVZ7XzazRU=">AAAHPnicfVVdb9s2FFW7zeu0r3R53Au71MBQ2I6VIksyIICBFcUKtFg2O22ByM0o6spiTVIaSTV2Cf2WvW7/Yn9jf2Bvw173uEvbWSwnGwFbFHnPObyXR2RSCm5sv//7rdvvvPte6/07H4QffvTxJ59u3f3suSkqzeCUFaLQLxNqQHAFp5ZbAS9LDVQmAl4k02/8/Is3oA0v1MjOSxhLOlE844xaHDrf2r4fs6o8d6+Po/qVm9bD89f3z7d2+r3+opHrnWjV2QlW7eT8bms7TgtWSVCWCWrMWdQv7dhRbTkTUIdxZaCkbEoncIZdRSWYsVusviZtHElJVmj8KUsWo+E6BHk0nTdYnKVJJaieNUeTopjijKnDsKlps8Ox46qsLCi2lMwqQWxBfFFIyjUwK+akqWv59G1HcQaZpqxDpZHU5p2S+3V27PRtd6JpmXcknQIDIa6GlqvycMETTfXcp1BcmE6CzBNdVCo1nZJaC1oZxFvNZx2T0xJMJ+O2w6hg/j31mFIUVlI9Nf/F2pNgKU4uKifAulGVWfgB0tppSO8d9u8lAnXXI2wOEw2gard4+JiLnFvYiElEBbXz/2sRYZvk1pbm691dC7OescgNM5ZTNYEeK+TuTxUY7y6zG321f7R3tGtAcjRhgp6T3Qtu865PostVN0Grgl7EPTzYWT7C2BeUopV9fcJ4IoqEihhfYw8bgDKVhkFaCDTAAI3MihSOYw2Czi6xBS6+aaKzUTR2fuO8ARq7fDIaUuWLq0HBBSYgqUpdnFHJxTyFjFbC1i422WW/aRKTeVfUYXtdzOAOQnrc7x11mOQoirYQaHkUsDOTeYpmksgdKzvzVIMl2JkHZ/it7Y/rzaQeAX5kGoZzmRTiMabkliymdt89e1o75SUkr52sHcflxkOwNwXjQLoJSVaQlYYHDKsEt9NWfktvFthUGD5+5ktyKTCKGuVzyax2RlyJ+OAl2j3BSF8DKsqc1ldL/fHJRtXTiQDO8u6y9jfN4EYbPF6a54P0NOu7LId8IlEpXrrK07k4kS5ejtfXbCGf4uGa3oRYTdRNiQfxLKH6DM0X50kxc/Eb/98O41xXAkgOfJJbPF0P9ktL2mSUA6HMVlQQhIXxFE+Ifm9vH2Ztctna5BFeDFQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBt9+LQLYv0cO80FgdriakUARNRQRklhiegkes5bUT1f+S4AXw8H9J9CKTBUvtq4DXSLR5aVzvPN/rRbi87/d2BoerC+VO8HnwRfBlEAUHwSD4NjgJTgMWzIOfg1+CX1u/tf5o/dn6axl6+9YKsx00WuvvfwAkCY0R</latexit>
N = ;<latexit sha1_base64="cCQugb7Mu1I9KkNyw7/c0OFwvuY=">AAAHOnicfVVdb9s2FFW7zeu0j6br417YpQaGwnbsFFmaAQGMrShWoN2y2WkLWEZKSVcSYZLSSKqRS+iX7HX7F/sje93bsNf9gF1azmI52QjYosh7zuG9PCLDgjNthsPfb9x85933Ou/f+sD/8KOPP7m9c+fTFzovVQSnUc5z9SqkGjiTcGqY4fCqUEBFyOFluPjGzb98A0qzXE7NsoC5oKlkCYuowaGzndv3vyPHJABRmKUGc/9sZ3c4GK4audoZrTu73rqdnN3p3A3iPCoFSBNxqvVsNCzM3FJlWMSh9oNSQ0GjBU1hhl1JBei5Xa28Jl0ciUmSK/xJQ1aj/iYEeRRdtlisoWHJqarao2GeL3BG177f1jTJo7llsigNyKiRTEpOTE5cQUjMFESGL0lb17DF255kESSKRj0qtKAm6xXMrbNnFm/7qaJF1hN0ARFwfjnUrMrBOQsVVUuXQn6ueyEypyovZax7BTUGlNSIN4pVPZ3RAnQvYaYXUR6599hhCp4bQdVC/xfrQIChOLmqHAdjp2Vi4EeIa6sgvvdoeC/kqLsZYTJIFYCs7erhYs4zZmArJuQl1Nb9b0T4XZIZU+iv9vYMVANtkBuqKKMyhUGUi72fStDOWXpv9OXB0f7RngbB0IAh+k30z5nJ+i6JPpP9EG0KahX38HC3efiBKyhFG7v6+EHK85DyAF8DBxuD1KWCcZxzNMAYTRzlMRwHCjitLrA5Lr5totl0NLdu45wBWrt8Mp1Q6YqrQMI5JiCojG2QUMH4MoaEltzUNtDJRb9tEp04V9R+d1NM4w5CfDwcHPUiwVAUbcHR8ihgKp04inaSyB1IUzmqcQO2+sEMv7WDeb2d1GPAj0zBZCnCnD/BlGzDomv7/fNntZVOQrDaitoyXG4wAXNdMA7E25BwDVlrOMCkDHE7Tem29HqBbYXJk+euJBcC01GrfDasaqv5pYgLbtD2KUa6GlBeZLS+XOrrp1tVj1MOLMr6Te2vm8GN1ni8tM8H4Wg2d1lMWCpQKWhc5ehsEAobNOP1FVuIZ3iwxtch1hN1W+JBUIVUzdB8QRbmlQ3euP+uH2Sq5EAyYGlm8HQ9PCgM6ZJpBoRGpqScIMwPFnhCDAf7B1B1yUXrksd4KVAZAQnBnOP362IJihG9KqPfSHV9QlYE/eFgBKJ7gZ5kucLqMJmSXBI0FeGQGKJZDA6xkdfuqP6XBC+Ah/9LolaZrFhqVwW8Rkbbl8bVzov9wQiX98P+7vjr9YVyy/vM+9z7wht5h97Y+9Y78U69yCu9n71fvF87v3X+6PzZ+asJvXljjbnrtVrn738AcTqK5Q==</latexit><latexit sha1_base64="cCQugb7Mu1I9KkNyw7/c0OFwvuY=">AAAHOnicfVVdb9s2FFW7zeu0j6br417YpQaGwnbsFFmaAQGMrShWoN2y2WkLWEZKSVcSYZLSSKqRS+iX7HX7F/sje93bsNf9gF1azmI52QjYosh7zuG9PCLDgjNthsPfb9x85933Ou/f+sD/8KOPP7m9c+fTFzovVQSnUc5z9SqkGjiTcGqY4fCqUEBFyOFluPjGzb98A0qzXE7NsoC5oKlkCYuowaGzndv3vyPHJABRmKUGc/9sZ3c4GK4audoZrTu73rqdnN3p3A3iPCoFSBNxqvVsNCzM3FJlWMSh9oNSQ0GjBU1hhl1JBei5Xa28Jl0ciUmSK/xJQ1aj/iYEeRRdtlisoWHJqarao2GeL3BG177f1jTJo7llsigNyKiRTEpOTE5cQUjMFESGL0lb17DF255kESSKRj0qtKAm6xXMrbNnFm/7qaJF1hN0ARFwfjnUrMrBOQsVVUuXQn6ueyEypyovZax7BTUGlNSIN4pVPZ3RAnQvYaYXUR6599hhCp4bQdVC/xfrQIChOLmqHAdjp2Vi4EeIa6sgvvdoeC/kqLsZYTJIFYCs7erhYs4zZmArJuQl1Nb9b0T4XZIZU+iv9vYMVANtkBuqKKMyhUGUi72fStDOWXpv9OXB0f7RngbB0IAh+k30z5nJ+i6JPpP9EG0KahX38HC3efiBKyhFG7v6+EHK85DyAF8DBxuD1KWCcZxzNMAYTRzlMRwHCjitLrA5Lr5totl0NLdu45wBWrt8Mp1Q6YqrQMI5JiCojG2QUMH4MoaEltzUNtDJRb9tEp04V9R+d1NM4w5CfDwcHPUiwVAUbcHR8ihgKp04inaSyB1IUzmqcQO2+sEMv7WDeb2d1GPAj0zBZCnCnD/BlGzDomv7/fNntZVOQrDaitoyXG4wAXNdMA7E25BwDVlrOMCkDHE7Tem29HqBbYXJk+euJBcC01GrfDasaqv5pYgLbtD2KUa6GlBeZLS+XOrrp1tVj1MOLMr6Te2vm8GN1ni8tM8H4Wg2d1lMWCpQKWhc5ehsEAobNOP1FVuIZ3iwxtch1hN1W+JBUIVUzdB8QRbmlQ3euP+uH2Sq5EAyYGlm8HQ9PCgM6ZJpBoRGpqScIMwPFnhCDAf7B1B1yUXrksd4KVAZAQnBnOP362IJihG9KqPfSHV9QlYE/eFgBKJ7gZ5kucLqMJmSXBI0FeGQGKJZDA6xkdfuqP6XBC+Ah/9LolaZrFhqVwW8Rkbbl8bVzov9wQiX98P+7vjr9YVyy/vM+9z7wht5h97Y+9Y78U69yCu9n71fvF87v3X+6PzZ+asJvXljjbnrtVrn738AcTqK5Q==</latexit><latexit sha1_base64="cCQugb7Mu1I9KkNyw7/c0OFwvuY=">AAAHOnicfVVdb9s2FFW7zeu0j6br417YpQaGwnbsFFmaAQGMrShWoN2y2WkLWEZKSVcSYZLSSKqRS+iX7HX7F/sje93bsNf9gF1azmI52QjYosh7zuG9PCLDgjNthsPfb9x85933Ou/f+sD/8KOPP7m9c+fTFzovVQSnUc5z9SqkGjiTcGqY4fCqUEBFyOFluPjGzb98A0qzXE7NsoC5oKlkCYuowaGzndv3vyPHJABRmKUGc/9sZ3c4GK4audoZrTu73rqdnN3p3A3iPCoFSBNxqvVsNCzM3FJlWMSh9oNSQ0GjBU1hhl1JBei5Xa28Jl0ciUmSK/xJQ1aj/iYEeRRdtlisoWHJqarao2GeL3BG177f1jTJo7llsigNyKiRTEpOTE5cQUjMFESGL0lb17DF255kESSKRj0qtKAm6xXMrbNnFm/7qaJF1hN0ARFwfjnUrMrBOQsVVUuXQn6ueyEypyovZax7BTUGlNSIN4pVPZ3RAnQvYaYXUR6599hhCp4bQdVC/xfrQIChOLmqHAdjp2Vi4EeIa6sgvvdoeC/kqLsZYTJIFYCs7erhYs4zZmArJuQl1Nb9b0T4XZIZU+iv9vYMVANtkBuqKKMyhUGUi72fStDOWXpv9OXB0f7RngbB0IAh+k30z5nJ+i6JPpP9EG0KahX38HC3efiBKyhFG7v6+EHK85DyAF8DBxuD1KWCcZxzNMAYTRzlMRwHCjitLrA5Lr5totl0NLdu45wBWrt8Mp1Q6YqrQMI5JiCojG2QUMH4MoaEltzUNtDJRb9tEp04V9R+d1NM4w5CfDwcHPUiwVAUbcHR8ihgKp04inaSyB1IUzmqcQO2+sEMv7WDeb2d1GPAj0zBZCnCnD/BlGzDomv7/fNntZVOQrDaitoyXG4wAXNdMA7E25BwDVlrOMCkDHE7Tem29HqBbYXJk+euJBcC01GrfDasaqv5pYgLbtD2KUa6GlBeZLS+XOrrp1tVj1MOLMr6Te2vm8GN1ni8tM8H4Wg2d1lMWCpQKWhc5ehsEAobNOP1FVuIZ3iwxtch1hN1W+JBUIVUzdB8QRbmlQ3euP+uH2Sq5EAyYGlm8HQ9PCgM6ZJpBoRGpqScIMwPFnhCDAf7B1B1yUXrksd4KVAZAQnBnOP362IJihG9KqPfSHV9QlYE/eFgBKJ7gZ5kucLqMJmSXBI0FeGQGKJZDA6xkdfuqP6XBC+Ah/9LolaZrFhqVwW8Rkbbl8bVzov9wQiX98P+7vjr9YVyy/vM+9z7wht5h97Y+9Y78U69yCu9n71fvF87v3X+6PzZ+asJvXljjbnrtVrn738AcTqK5Q==</latexit><latexit sha1_base64="cCQugb7Mu1I9KkNyw7/c0OFwvuY=">AAAHOnicfVVdb9s2FFW7zeu0j6br417YpQaGwnbsFFmaAQGMrShWoN2y2WkLWEZKSVcSYZLSSKqRS+iX7HX7F/sje93bsNf9gF1azmI52QjYosh7zuG9PCLDgjNthsPfb9x85933Ou/f+sD/8KOPP7m9c+fTFzovVQSnUc5z9SqkGjiTcGqY4fCqUEBFyOFluPjGzb98A0qzXE7NsoC5oKlkCYuowaGzndv3vyPHJABRmKUGc/9sZ3c4GK4audoZrTu73rqdnN3p3A3iPCoFSBNxqvVsNCzM3FJlWMSh9oNSQ0GjBU1hhl1JBei5Xa28Jl0ciUmSK/xJQ1aj/iYEeRRdtlisoWHJqarao2GeL3BG177f1jTJo7llsigNyKiRTEpOTE5cQUjMFESGL0lb17DF255kESSKRj0qtKAm6xXMrbNnFm/7qaJF1hN0ARFwfjnUrMrBOQsVVUuXQn6ueyEypyovZax7BTUGlNSIN4pVPZ3RAnQvYaYXUR6599hhCp4bQdVC/xfrQIChOLmqHAdjp2Vi4EeIa6sgvvdoeC/kqLsZYTJIFYCs7erhYs4zZmArJuQl1Nb9b0T4XZIZU+iv9vYMVANtkBuqKKMyhUGUi72fStDOWXpv9OXB0f7RngbB0IAh+k30z5nJ+i6JPpP9EG0KahX38HC3efiBKyhFG7v6+EHK85DyAF8DBxuD1KWCcZxzNMAYTRzlMRwHCjitLrA5Lr5totl0NLdu45wBWrt8Mp1Q6YqrQMI5JiCojG2QUMH4MoaEltzUNtDJRb9tEp04V9R+d1NM4w5CfDwcHPUiwVAUbcHR8ihgKp04inaSyB1IUzmqcQO2+sEMv7WDeb2d1GPAj0zBZCnCnD/BlGzDomv7/fNntZVOQrDaitoyXG4wAXNdMA7E25BwDVlrOMCkDHE7Tem29HqBbYXJk+euJBcC01GrfDasaqv5pYgLbtD2KUa6GlBeZLS+XOrrp1tVj1MOLMr6Te2vm8GN1ni8tM8H4Wg2d1lMWCpQKWhc5ehsEAobNOP1FVuIZ3iwxtch1hN1W+JBUIVUzdB8QRbmlQ3euP+uH2Sq5EAyYGlm8HQ9PCgM6ZJpBoRGpqScIMwPFnhCDAf7B1B1yUXrksd4KVAZAQnBnOP362IJihG9KqPfSHV9QlYE/eFgBKJ7gZ5kucLqMJmSXBI0FeGQGKJZDA6xkdfuqP6XBC+Ah/9LolaZrFhqVwW8Rkbbl8bVzov9wQiX98P+7vjr9YVyy/vM+9z7wht5h97Y+9Y78U69yCu9n71fvF87v3X+6PzZ+asJvXljjbnrtVrn738AcTqK5Q==</latexit>
N = N [ T<latexit sha1_base64="+8IXgngcg4Tx80sHc3gtOzbENVM=">AAAHN3icfVVdjxs1FJ0WCGX4aukjLy7bSKhKsslWy3aRVoqgqqjUloVk20o7oXg8d2as2J7B9nQnteZ/8Ar/gp/CE2+IV/4B10mWzWQXLCXjse85x/f6jB2Xghs7HP5+7fpbb7/TeffGe+H7H3z40cc3b33y3BSVZnDCClHolzE1ILiCE8utgJelBipjAS/i+dd+/sVr0IYXamoXJcwkzRRPOaMWh364+4wckWckYlVJpndf3dwZDobLRi53RuvOTrBux69udW5HScEqCcoyQY05HQ1LO3NUW84ENGFUGSgpm9MMTrGrqAQzc8tlN6SLIwlJC40/ZclyNNyEII+mixaLszSuBNV1ezQuijnOmCYM25o2fTBzXJWVBcVWkmkliC2IrwZJuAZmxYK0dS2fv+kpziDVlPWoNJLavFdyv86enb/pZ5qWeU/SOTAQ4mJotSoPFzzWVC98CsWZ6cXInOmiUonpldRa0Mog3mpe90xOSzC9lNseo4L598RjSlFYSfXc/BfrQIKlOLmsnADrplVq4XtIGqchufNgeCcWqLsZYXPINIBq3PLhY85ybmErJhYVNM7/b0SEXZJbW5ovd3ct1ANjkRtqllOVwYAVcvenCoy3ldkdfbF/uHe4a0BydF+MZpP9M27zvk+iz1U/Ro+CXsbdP9hZPcLIF5Sih319wigTRUxFhK+Rh41BmUrDOCkEGmCMDmZFAkeRBkHrc2yBi2+b6HQ6mjm/cd4ArV0+nk6o8sXVoOAME5BUJS5KqeRikUBKK2EbF5n0vN82iUm9K5qwuylmcAchORoODntMchRFWwi0PArY2qSeop0kckfK1p5qvAI7c+8Uv7X9WbOd1EPAj0zDZCHjQjzClNyKxTTu26dPGqe8hOSNk43juNxoAvaqYBxItiHxGrLW8IBJFeN22spv6dUC2wqTR099Sc4FpqNW+VxcN86ICxEfvEK7xxjpa0BFmdPmYqk/Pt6qepIJ4Czvr2p/1QxutMHjpX0+SE+zuctywjOJStHKVZ7ORbF00Wq8uWQL+QRP1eQqxHqiaUvci+qY6lM0X5THRe2i1/6/G0a5rgSQHHiWWzxdD/ZLS7pkmgOhzFZUEISF0RxPiOFgbx/qLjlvXfIQbwSqGJAY7Bl+vz6WoBgxyzKGK6luSMiSoD8cjEB2z9GTvNBYHa4yUiiCpiICUksMT8AjNvLaGTX/kuAFcP9/SfQykyVL46uA18ho+9K43Hm+Nxjh8r7b2xl/tb5QbgSfBp8Fnwej4CAYB98Ex8FJwAId/Bz8Evza+a3zR+fPzl+r0OvX1pjbQat1/v4HOH2JWQ==</latexit><latexit sha1_base64="+8IXgngcg4Tx80sHc3gtOzbENVM=">AAAHN3icfVVdjxs1FJ0WCGX4aukjLy7bSKhKsslWy3aRVoqgqqjUloVk20o7oXg8d2as2J7B9nQnteZ/8Ar/gp/CE2+IV/4B10mWzWQXLCXjse85x/f6jB2Xghs7HP5+7fpbb7/TeffGe+H7H3z40cc3b33y3BSVZnDCClHolzE1ILiCE8utgJelBipjAS/i+dd+/sVr0IYXamoXJcwkzRRPOaMWh364+4wckWckYlVJpndf3dwZDobLRi53RuvOTrBux69udW5HScEqCcoyQY05HQ1LO3NUW84ENGFUGSgpm9MMTrGrqAQzc8tlN6SLIwlJC40/ZclyNNyEII+mixaLszSuBNV1ezQuijnOmCYM25o2fTBzXJWVBcVWkmkliC2IrwZJuAZmxYK0dS2fv+kpziDVlPWoNJLavFdyv86enb/pZ5qWeU/SOTAQ4mJotSoPFzzWVC98CsWZ6cXInOmiUonpldRa0Mog3mpe90xOSzC9lNseo4L598RjSlFYSfXc/BfrQIKlOLmsnADrplVq4XtIGqchufNgeCcWqLsZYXPINIBq3PLhY85ybmErJhYVNM7/b0SEXZJbW5ovd3ct1ANjkRtqllOVwYAVcvenCoy3ldkdfbF/uHe4a0BydF+MZpP9M27zvk+iz1U/Ro+CXsbdP9hZPcLIF5Sih319wigTRUxFhK+Rh41BmUrDOCkEGmCMDmZFAkeRBkHrc2yBi2+b6HQ6mjm/cd4ArV0+nk6o8sXVoOAME5BUJS5KqeRikUBKK2EbF5n0vN82iUm9K5qwuylmcAchORoODntMchRFWwi0PArY2qSeop0kckfK1p5qvAI7c+8Uv7X9WbOd1EPAj0zDZCHjQjzClNyKxTTu26dPGqe8hOSNk43juNxoAvaqYBxItiHxGrLW8IBJFeN22spv6dUC2wqTR099Sc4FpqNW+VxcN86ICxEfvEK7xxjpa0BFmdPmYqk/Pt6qepIJ4Czvr2p/1QxutMHjpX0+SE+zuctywjOJStHKVZ7ORbF00Wq8uWQL+QRP1eQqxHqiaUvci+qY6lM0X5THRe2i1/6/G0a5rgSQHHiWWzxdD/ZLS7pkmgOhzFZUEISF0RxPiOFgbx/qLjlvXfIQbwSqGJAY7Bl+vz6WoBgxyzKGK6luSMiSoD8cjEB2z9GTvNBYHa4yUiiCpiICUksMT8AjNvLaGTX/kuAFcP9/SfQykyVL46uA18ho+9K43Hm+Nxjh8r7b2xl/tb5QbgSfBp8Fnwej4CAYB98Ex8FJwAId/Bz8Evza+a3zR+fPzl+r0OvX1pjbQat1/v4HOH2JWQ==</latexit><latexit sha1_base64="+8IXgngcg4Tx80sHc3gtOzbENVM=">AAAHN3icfVVdjxs1FJ0WCGX4aukjLy7bSKhKsslWy3aRVoqgqqjUloVk20o7oXg8d2as2J7B9nQnteZ/8Ar/gp/CE2+IV/4B10mWzWQXLCXjse85x/f6jB2Xghs7HP5+7fpbb7/TeffGe+H7H3z40cc3b33y3BSVZnDCClHolzE1ILiCE8utgJelBipjAS/i+dd+/sVr0IYXamoXJcwkzRRPOaMWh364+4wckWckYlVJpndf3dwZDobLRi53RuvOTrBux69udW5HScEqCcoyQY05HQ1LO3NUW84ENGFUGSgpm9MMTrGrqAQzc8tlN6SLIwlJC40/ZclyNNyEII+mixaLszSuBNV1ezQuijnOmCYM25o2fTBzXJWVBcVWkmkliC2IrwZJuAZmxYK0dS2fv+kpziDVlPWoNJLavFdyv86enb/pZ5qWeU/SOTAQ4mJotSoPFzzWVC98CsWZ6cXInOmiUonpldRa0Mog3mpe90xOSzC9lNseo4L598RjSlFYSfXc/BfrQIKlOLmsnADrplVq4XtIGqchufNgeCcWqLsZYXPINIBq3PLhY85ybmErJhYVNM7/b0SEXZJbW5ovd3ct1ANjkRtqllOVwYAVcvenCoy3ldkdfbF/uHe4a0BydF+MZpP9M27zvk+iz1U/Ro+CXsbdP9hZPcLIF5Sih319wigTRUxFhK+Rh41BmUrDOCkEGmCMDmZFAkeRBkHrc2yBi2+b6HQ6mjm/cd4ArV0+nk6o8sXVoOAME5BUJS5KqeRikUBKK2EbF5n0vN82iUm9K5qwuylmcAchORoODntMchRFWwi0PArY2qSeop0kckfK1p5qvAI7c+8Uv7X9WbOd1EPAj0zDZCHjQjzClNyKxTTu26dPGqe8hOSNk43juNxoAvaqYBxItiHxGrLW8IBJFeN22spv6dUC2wqTR099Sc4FpqNW+VxcN86ICxEfvEK7xxjpa0BFmdPmYqk/Pt6qepIJ4Czvr2p/1QxutMHjpX0+SE+zuctywjOJStHKVZ7ORbF00Wq8uWQL+QRP1eQqxHqiaUvci+qY6lM0X5THRe2i1/6/G0a5rgSQHHiWWzxdD/ZLS7pkmgOhzFZUEISF0RxPiOFgbx/qLjlvXfIQbwSqGJAY7Bl+vz6WoBgxyzKGK6luSMiSoD8cjEB2z9GTvNBYHa4yUiiCpiICUksMT8AjNvLaGTX/kuAFcP9/SfQykyVL46uA18ho+9K43Hm+Nxjh8r7b2xl/tb5QbgSfBp8Fnwej4CAYB98Ex8FJwAId/Bz8Evza+a3zR+fPzl+r0OvX1pjbQat1/v4HOH2JWQ==</latexit><latexit sha1_base64="+8IXgngcg4Tx80sHc3gtOzbENVM=">AAAHN3icfVVdjxs1FJ0WCGX4aukjLy7bSKhKsslWy3aRVoqgqqjUloVk20o7oXg8d2as2J7B9nQnteZ/8Ar/gp/CE2+IV/4B10mWzWQXLCXjse85x/f6jB2Xghs7HP5+7fpbb7/TeffGe+H7H3z40cc3b33y3BSVZnDCClHolzE1ILiCE8utgJelBipjAS/i+dd+/sVr0IYXamoXJcwkzRRPOaMWh364+4wckWckYlVJpndf3dwZDobLRi53RuvOTrBux69udW5HScEqCcoyQY05HQ1LO3NUW84ENGFUGSgpm9MMTrGrqAQzc8tlN6SLIwlJC40/ZclyNNyEII+mixaLszSuBNV1ezQuijnOmCYM25o2fTBzXJWVBcVWkmkliC2IrwZJuAZmxYK0dS2fv+kpziDVlPWoNJLavFdyv86enb/pZ5qWeU/SOTAQ4mJotSoPFzzWVC98CsWZ6cXInOmiUonpldRa0Mog3mpe90xOSzC9lNseo4L598RjSlFYSfXc/BfrQIKlOLmsnADrplVq4XtIGqchufNgeCcWqLsZYXPINIBq3PLhY85ybmErJhYVNM7/b0SEXZJbW5ovd3ct1ANjkRtqllOVwYAVcvenCoy3ldkdfbF/uHe4a0BydF+MZpP9M27zvk+iz1U/Ro+CXsbdP9hZPcLIF5Sih319wigTRUxFhK+Rh41BmUrDOCkEGmCMDmZFAkeRBkHrc2yBi2+b6HQ6mjm/cd4ArV0+nk6o8sXVoOAME5BUJS5KqeRikUBKK2EbF5n0vN82iUm9K5qwuylmcAchORoODntMchRFWwi0PArY2qSeop0kckfK1p5qvAI7c+8Uv7X9WbOd1EPAj0zDZCHjQjzClNyKxTTu26dPGqe8hOSNk43juNxoAvaqYBxItiHxGrLW8IBJFeN22spv6dUC2wqTR099Sc4FpqNW+VxcN86ICxEfvEK7xxjpa0BFmdPmYqk/Pt6qepIJ4Czvr2p/1QxutMHjpX0+SE+zuctywjOJStHKVZ7ORbF00Wq8uWQL+QRP1eQqxHqiaUvci+qY6lM0X5THRe2i1/6/G0a5rgSQHHiWWzxdD/ZLS7pkmgOhzFZUEISF0RxPiOFgbx/qLjlvXfIQbwSqGJAY7Bl+vz6WoBgxyzKGK6luSMiSoD8cjEB2z9GTvNBYHa4yUiiCpiICUksMT8AjNvLaGTX/kuAFcP9/SfQykyVL46uA18ho+9K43Hm+Nxjh8r7b2xl/tb5QbgSfBp8Fnwej4CAYB98Ex8FJwAId/Bz8Evza+a3zR+fPzl+r0OvX1pjbQat1/v4HOH2JWQ==</latexit>
|N| = r<latexit sha1_base64="tQEGT1dKiB0d6p4CljzChDc5oR0=">AAAHQHicfVVdb9s2FFW7zeu0j6Yr9rQXdqmBoZAdO0WWZkAAYyuKFWi3bHbaApaRUdKVRJikNJJq5BL6MXvd/sX+xf7B3oa97mmXtrNYTjYCtijynnN4L4/IqORMm8Hg9xs333r7nc67t97z3//gw49u79z5+IUuKhXDaVzwQr2KqAbOJJwaZji8KhVQEXF4Gc2/dvMvX4PSrJATsyhhJmgmWcpianDobOeT+yHHeUO+JaFado6Jun+2szvoD5aNXO0M151db91Ozu507oZJEVcCpIk51Xo6HJRmZqkyLObQ+GGloaTxnGYwxa6kAvTMLtffkC6OJCQtFP6kIctRfxOCPIouWizW0KjiVNXt0ago5jijG99va5r00cwyWVYGZLySTCtOTEFcWUjCFMSGL0hb17D5m0CyGFJF44AKLajJg5K5dQZm/qaXKVrmgaBziIHzy6HVqhycs0hRtXApFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaq7/i7UvwFCcXFaOg7GTKjXwAySNVZDcezS4F3HU3YwwOWQKQDZ2+XAx5zkzsBUT8Qoa6/43IvwuyY0p9Zd7ewbqvjbIDXWcU5lBPy7E3k8VaOcvvTf84uBo/2hPg2DorghdJ3rnzOQ9l0SPyV6EZgW1jHt4uLt6+KErKEUzu/r4YcaLiPIQX0MHG4HUlYJRUnA0wAitHBcJHIcKOK0vsAUuvm2i6WQ4s27jnAFau3wyGVPpiqtAwjkmIKhMbJhSwfgigZRW3DQ21OlFv20SnTpXNH53U0zjDkJyPOgfBbFgKIq24Gh5FDC1Th1FO0nkDqWpHdVoBbb6wRS/tYNZs53UY8CPTMF4IaKCP8GU7IpFN/a7588aK52EYI0VjWW43HAM5rpgHEi2IdEastZwgHEV4Xaaym3p9QLbCuMnz11JLgQmw1b5bFQ3VvNLERe8QtunGOlqQHmZ0+ZyqT8+3ap6knFgcd5b1f66GdxojcdL+3wQjmZzl8WYZQKVwpWrHJ0NI2HD1XhzxRbiGR6vyXWI9UTTlngQ1hFVUzRfmEdFbcPX7r/rh7mqOJAcWJYbPF0PD0pDumSSA6GxqSgnCPPDOZ4Qg/7+AdRdctG65DFeDVTGQCIw5/j9uliCYkQvy+ivpLo+IUuC3qA/BNG9QI/zQmF1mMxIIQmainBIDdEsAYfYyGt32PxLghfAw/8lUctMliyNqwJeI8PtS+Nq58V+f4jL+35/d/TV+kK55X3qfeZ97g29Q2/kfeOdeKde7FnvZ+8X79fOb50/On92/lqF3ryxxtz1Wq3z9z/OTY0U</latexit><latexit sha1_base64="tQEGT1dKiB0d6p4CljzChDc5oR0=">AAAHQHicfVVdb9s2FFW7zeu0j6Yr9rQXdqmBoZAdO0WWZkAAYyuKFWi3bHbaApaRUdKVRJikNJJq5BL6MXvd/sX+xf7B3oa97mmXtrNYTjYCtijynnN4L4/IqORMm8Hg9xs333r7nc67t97z3//gw49u79z5+IUuKhXDaVzwQr2KqAbOJJwaZji8KhVQEXF4Gc2/dvMvX4PSrJATsyhhJmgmWcpianDobOeT+yHHeUO+JaFado6Jun+2szvoD5aNXO0M151db91Ozu507oZJEVcCpIk51Xo6HJRmZqkyLObQ+GGloaTxnGYwxa6kAvTMLtffkC6OJCQtFP6kIctRfxOCPIouWizW0KjiVNXt0ago5jijG99va5r00cwyWVYGZLySTCtOTEFcWUjCFMSGL0hb17D5m0CyGFJF44AKLajJg5K5dQZm/qaXKVrmgaBziIHzy6HVqhycs0hRtXApFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaq7/i7UvwFCcXFaOg7GTKjXwAySNVZDcezS4F3HU3YwwOWQKQDZ2+XAx5zkzsBUT8Qoa6/43IvwuyY0p9Zd7ewbqvjbIDXWcU5lBPy7E3k8VaOcvvTf84uBo/2hPg2DorghdJ3rnzOQ9l0SPyV6EZgW1jHt4uLt6+KErKEUzu/r4YcaLiPIQX0MHG4HUlYJRUnA0wAitHBcJHIcKOK0vsAUuvm2i6WQ4s27jnAFau3wyGVPpiqtAwjkmIKhMbJhSwfgigZRW3DQ21OlFv20SnTpXNH53U0zjDkJyPOgfBbFgKIq24Gh5FDC1Th1FO0nkDqWpHdVoBbb6wRS/tYNZs53UY8CPTMF4IaKCP8GU7IpFN/a7588aK52EYI0VjWW43HAM5rpgHEi2IdEastZwgHEV4Xaaym3p9QLbCuMnz11JLgQmw1b5bFQ3VvNLERe8QtunGOlqQHmZ0+ZyqT8+3ap6knFgcd5b1f66GdxojcdL+3wQjmZzl8WYZQKVwpWrHJ0NI2HD1XhzxRbiGR6vyXWI9UTTlngQ1hFVUzRfmEdFbcPX7r/rh7mqOJAcWJYbPF0PD0pDumSSA6GxqSgnCPPDOZ4Qg/7+AdRdctG65DFeDVTGQCIw5/j9uliCYkQvy+ivpLo+IUuC3qA/BNG9QI/zQmF1mMxIIQmainBIDdEsAYfYyGt32PxLghfAw/8lUctMliyNqwJeI8PtS+Nq58V+f4jL+35/d/TV+kK55X3qfeZ97g29Q2/kfeOdeKde7FnvZ+8X79fOb50/On92/lqF3ryxxtz1Wq3z9z/OTY0U</latexit><latexit sha1_base64="tQEGT1dKiB0d6p4CljzChDc5oR0=">AAAHQHicfVVdb9s2FFW7zeu0j6Yr9rQXdqmBoZAdO0WWZkAAYyuKFWi3bHbaApaRUdKVRJikNJJq5BL6MXvd/sX+xf7B3oa97mmXtrNYTjYCtijynnN4L4/IqORMm8Hg9xs333r7nc67t97z3//gw49u79z5+IUuKhXDaVzwQr2KqAbOJJwaZji8KhVQEXF4Gc2/dvMvX4PSrJATsyhhJmgmWcpianDobOeT+yHHeUO+JaFado6Jun+2szvoD5aNXO0M151db91Ozu507oZJEVcCpIk51Xo6HJRmZqkyLObQ+GGloaTxnGYwxa6kAvTMLtffkC6OJCQtFP6kIctRfxOCPIouWizW0KjiVNXt0ago5jijG99va5r00cwyWVYGZLySTCtOTEFcWUjCFMSGL0hb17D5m0CyGFJF44AKLajJg5K5dQZm/qaXKVrmgaBziIHzy6HVqhycs0hRtXApFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaq7/i7UvwFCcXFaOg7GTKjXwAySNVZDcezS4F3HU3YwwOWQKQDZ2+XAx5zkzsBUT8Qoa6/43IvwuyY0p9Zd7ewbqvjbIDXWcU5lBPy7E3k8VaOcvvTf84uBo/2hPg2DorghdJ3rnzOQ9l0SPyV6EZgW1jHt4uLt6+KErKEUzu/r4YcaLiPIQX0MHG4HUlYJRUnA0wAitHBcJHIcKOK0vsAUuvm2i6WQ4s27jnAFau3wyGVPpiqtAwjkmIKhMbJhSwfgigZRW3DQ21OlFv20SnTpXNH53U0zjDkJyPOgfBbFgKIq24Gh5FDC1Th1FO0nkDqWpHdVoBbb6wRS/tYNZs53UY8CPTMF4IaKCP8GU7IpFN/a7588aK52EYI0VjWW43HAM5rpgHEi2IdEastZwgHEV4Xaaym3p9QLbCuMnz11JLgQmw1b5bFQ3VvNLERe8QtunGOlqQHmZ0+ZyqT8+3ap6knFgcd5b1f66GdxojcdL+3wQjmZzl8WYZQKVwpWrHJ0NI2HD1XhzxRbiGR6vyXWI9UTTlngQ1hFVUzRfmEdFbcPX7r/rh7mqOJAcWJYbPF0PD0pDumSSA6GxqSgnCPPDOZ4Qg/7+AdRdctG65DFeDVTGQCIw5/j9uliCYkQvy+ivpLo+IUuC3qA/BNG9QI/zQmF1mMxIIQmainBIDdEsAYfYyGt32PxLghfAw/8lUctMliyNqwJeI8PtS+Nq58V+f4jL+35/d/TV+kK55X3qfeZ97g29Q2/kfeOdeKde7FnvZ+8X79fOb50/On92/lqF3ryxxtz1Wq3z9z/OTY0U</latexit><latexit sha1_base64="tQEGT1dKiB0d6p4CljzChDc5oR0=">AAAHQHicfVVdb9s2FFW7zeu0j6Yr9rQXdqmBoZAdO0WWZkAAYyuKFWi3bHbaApaRUdKVRJikNJJq5BL6MXvd/sX+xf7B3oa97mmXtrNYTjYCtijynnN4L4/IqORMm8Hg9xs333r7nc67t97z3//gw49u79z5+IUuKhXDaVzwQr2KqAbOJJwaZji8KhVQEXF4Gc2/dvMvX4PSrJATsyhhJmgmWcpianDobOeT+yHHeUO+JaFado6Jun+2szvoD5aNXO0M151db91Ozu507oZJEVcCpIk51Xo6HJRmZqkyLObQ+GGloaTxnGYwxa6kAvTMLtffkC6OJCQtFP6kIctRfxOCPIouWizW0KjiVNXt0ago5jijG99va5r00cwyWVYGZLySTCtOTEFcWUjCFMSGL0hb17D5m0CyGFJF44AKLajJg5K5dQZm/qaXKVrmgaBziIHzy6HVqhycs0hRtXApFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaq7/i7UvwFCcXFaOg7GTKjXwAySNVZDcezS4F3HU3YwwOWQKQDZ2+XAx5zkzsBUT8Qoa6/43IvwuyY0p9Zd7ewbqvjbIDXWcU5lBPy7E3k8VaOcvvTf84uBo/2hPg2DorghdJ3rnzOQ9l0SPyV6EZgW1jHt4uLt6+KErKEUzu/r4YcaLiPIQX0MHG4HUlYJRUnA0wAitHBcJHIcKOK0vsAUuvm2i6WQ4s27jnAFau3wyGVPpiqtAwjkmIKhMbJhSwfgigZRW3DQ21OlFv20SnTpXNH53U0zjDkJyPOgfBbFgKIq24Gh5FDC1Th1FO0nkDqWpHdVoBbb6wRS/tYNZs53UY8CPTMF4IaKCP8GU7IpFN/a7588aK52EYI0VjWW43HAM5rpgHEi2IdEastZwgHEV4Xaaym3p9QLbCuMnz11JLgQmw1b5bFQ3VvNLERe8QtunGOlqQHmZ0+ZyqT8+3ap6knFgcd5b1f66GdxojcdL+3wQjmZzl8WYZQKVwpWrHJ0NI2HD1XhzxRbiGR6vyXWI9UTTlngQ1hFVUzRfmEdFbcPX7r/rh7mqOJAcWJYbPF0PD0pDumSSA6GxqSgnCPPDOZ4Qg/7+AdRdctG65DFeDVTGQCIw5/j9uliCYkQvy+ivpLo+IUuC3qA/BNG9QI/zQmF1mMxIIQmainBIDdEsAYfYyGt32PxLghfAw/8lUctMliyNqwJeI8PtS+Nq58V+f4jL+35/d/TV+kK55X3qfeZ97g29Q2/kfeOdeKde7FnvZ+8X79fOb50/On92/lqF3ryxxtz1Wq3z9z/OTY0U</latexit>

16. Our Correlated Repeat Unions (CRU) model captures
repeat behavior,recency bias,and correlations.
16
Setup (k = 3).
Observe S1, …, S3: {a, b}, {c}, {a, c, d}.
Given that S4 has 3 repeated elements.
Model selects three elements from {a, b, c, d}.
CRU model (p = 0.8; w1 = 0.6,w2 = 0.3 w3 = 0.1).
{a, b} w3 = 0.1{c} w2 = 0.3{a, c, d} w1 = 0.6
0. N = ;.<latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit><latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit><latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit><latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit>
1. N = {a, c}.<latexit sha1_base64="/m/3pGpI42L2jFUUwxh1JPMNRRA=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+83G/G39J7n1LjknsaERYXN/rhuc7u71ub9HI1U5/1dkNVu3k/HbrTpwWrJKgLBPUmLN+r7RjR7XlTEAdxpWBkrIpncAZdhWVYMZusf6atHEkJVmh8acsWYyGmxDk0XTeYHGWJpWgetYcTYpiijOmDsOmps0ejh1XZWVBsaVkVgliC+LLQlKugVkxJ01dy6evI8UZZJqyiEojqc2jkvt1Rnb6ujPRtMwjSafAQIjLoeWqPFzwRFM99ykUFyZKkHmii0qlJiqptaCVQbzVfBaZnJZgoozbiFHB/HvqMaUorKR6av6LtSvBUpxcVE6AdaMqs/ADpLXTkN592LubCNTdjLA5TDSAqt3i4WMucm5hKyYRFdTO/29EhG2SW1uaL/b2LMy6xiI3zFhO1QS6rJB7P1VgvL/MXv/zg6P9oz0DkqMNE3Sd7Fxwm3d8Eh2uOgmaFfQi7sHh7vIRxr6gFM3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBmhlVqRwHGsQdLbGFrj4ponORv2x8xvnDdDY5ZPRkCpfXA0KLjABSVXq4oxKLuYpZLQStnaxydb9pklM5l1Rh+1NMYM7COlxr3sUMclRFG0h0PIoYGcm8xTNJJE7VnbmqQZLsDP3z/BbOxjX20k9AvzINAznMinEY0zJLVlM7b579rR2yktIXjtZO47LjYdgrwvGgXQbkqwgKw0PGFYJbqet/JZeL7CtMHz8zJdkLTDqN8rnklntjLgU8cFLtHuCkb4GVJQ5rS+X+uOTraqnEwGc5Z1l7a+bwY02eLw0zwfpaTZ3WQ75RKJSvHSVp3NxIl28HK+v2EI+xeM1vQ6xmqibEvfjWUL1GZovzpNi5uJX/r8dxrmuBJAc+CS3eLoeHpSWtMkoB0KZraggCAvjKZ4Qve7+AczaZN3a5BFeDVQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBp9ftg2yv0cO80FgdriakUARNRQRklhiegkds5LXbr/8lwQvgwf+S6EUmC5baVwGvkf72pXG183y/28flfb+/O/hqdaHcCj4JPg0+C/rBYTAIvglOgtOABS74Ofgl+LX1W+uP1p+tv5ahN2+sMHeCRmv9/Q/4S4tY</latexit><latexit sha1_base64="/m/3pGpI42L2jFUUwxh1JPMNRRA=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+83G/G39J7n1LjknsaERYXN/rhuc7u71ub9HI1U5/1dkNVu3k/HbrTpwWrJKgLBPUmLN+r7RjR7XlTEAdxpWBkrIpncAZdhWVYMZusf6atHEkJVmh8acsWYyGmxDk0XTeYHGWJpWgetYcTYpiijOmDsOmps0ejh1XZWVBsaVkVgliC+LLQlKugVkxJ01dy6evI8UZZJqyiEojqc2jkvt1Rnb6ujPRtMwjSafAQIjLoeWqPFzwRFM99ykUFyZKkHmii0qlJiqptaCVQbzVfBaZnJZgoozbiFHB/HvqMaUorKR6av6LtSvBUpxcVE6AdaMqs/ADpLXTkN592LubCNTdjLA5TDSAqt3i4WMucm5hKyYRFdTO/29EhG2SW1uaL/b2LMy6xiI3zFhO1QS6rJB7P1VgvL/MXv/zg6P9oz0DkqMNE3Sd7Fxwm3d8Eh2uOgmaFfQi7sHh7vIRxr6gFM3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBmhlVqRwHGsQdLbGFrj4ponORv2x8xvnDdDY5ZPRkCpfXA0KLjABSVXq4oxKLuYpZLQStnaxydb9pklM5l1Rh+1NMYM7COlxr3sUMclRFG0h0PIoYGcm8xTNJJE7VnbmqQZLsDP3z/BbOxjX20k9AvzINAznMinEY0zJLVlM7b579rR2yktIXjtZO47LjYdgrwvGgXQbkqwgKw0PGFYJbqet/JZeL7CtMHz8zJdkLTDqN8rnklntjLgU8cFLtHuCkb4GVJQ5rS+X+uOTraqnEwGc5Z1l7a+bwY02eLw0zwfpaTZ3WQ75RKJSvHSVp3NxIl28HK+v2EI+xeM1vQ6xmqibEvfjWUL1GZovzpNi5uJX/r8dxrmuBJAc+CS3eLoeHpSWtMkoB0KZraggCAvjKZ4Qve7+AczaZN3a5BFeDVQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBp9ftg2yv0cO80FgdriakUARNRQRklhiegkds5LXbr/8lwQvgwf+S6EUmC5baVwGvkf72pXG183y/28flfb+/O/hqdaHcCj4JPg0+C/rBYTAIvglOgtOABS74Ofgl+LX1W+uP1p+tv5ahN2+sMHeCRmv9/Q/4S4tY</latexit><latexit sha1_base64="/m/3pGpI42L2jFUUwxh1JPMNRRA=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+83G/G39J7n1LjknsaERYXN/rhuc7u71ub9HI1U5/1dkNVu3k/HbrTpwWrJKgLBPUmLN+r7RjR7XlTEAdxpWBkrIpncAZdhWVYMZusf6atHEkJVmh8acsWYyGmxDk0XTeYHGWJpWgetYcTYpiijOmDsOmps0ejh1XZWVBsaVkVgliC+LLQlKugVkxJ01dy6evI8UZZJqyiEojqc2jkvt1Rnb6ujPRtMwjSafAQIjLoeWqPFzwRFM99ykUFyZKkHmii0qlJiqptaCVQbzVfBaZnJZgoozbiFHB/HvqMaUorKR6av6LtSvBUpxcVE6AdaMqs/ADpLXTkN592LubCNTdjLA5TDSAqt3i4WMucm5hKyYRFdTO/29EhG2SW1uaL/b2LMy6xiI3zFhO1QS6rJB7P1VgvL/MXv/zg6P9oz0DkqMNE3Sd7Fxwm3d8Eh2uOgmaFfQi7sHh7vIRxr6gFM3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBmhlVqRwHGsQdLbGFrj4ponORv2x8xvnDdDY5ZPRkCpfXA0KLjABSVXq4oxKLuYpZLQStnaxydb9pklM5l1Rh+1NMYM7COlxr3sUMclRFG0h0PIoYGcm8xTNJJE7VnbmqQZLsDP3z/BbOxjX20k9AvzINAznMinEY0zJLVlM7b579rR2yktIXjtZO47LjYdgrwvGgXQbkqwgKw0PGFYJbqet/JZeL7CtMHz8zJdkLTDqN8rnklntjLgU8cFLtHuCkb4GVJQ5rS+X+uOTraqnEwGc5Z1l7a+bwY02eLw0zwfpaTZ3WQ75RKJSvHSVp3NxIl28HK+v2EI+xeM1vQ6xmqibEvfjWUL1GZovzpNi5uJX/r8dxrmuBJAc+CS3eLoeHpSWtMkoB0KZraggCAvjKZ4Qve7+AczaZN3a5BFeDVQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBp9ftg2yv0cO80FgdriakUARNRQRklhiegkds5LXbr/8lwQvgwf+S6EUmC5baVwGvkf72pXG183y/28flfb+/O/hqdaHcCj4JPg0+C/rBYTAIvglOgtOABS74Ofgl+LX1W+uP1p+tv5ahN2+sMHeCRmv9/Q/4S4tY</latexit><latexit sha1_base64="/m/3pGpI42L2jFUUwxh1JPMNRRA=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+83G/G39J7n1LjknsaERYXN/rhuc7u71ub9HI1U5/1dkNVu3k/HbrTpwWrJKgLBPUmLN+r7RjR7XlTEAdxpWBkrIpncAZdhWVYMZusf6atHEkJVmh8acsWYyGmxDk0XTeYHGWJpWgetYcTYpiijOmDsOmps0ejh1XZWVBsaVkVgliC+LLQlKugVkxJ01dy6evI8UZZJqyiEojqc2jkvt1Rnb6ujPRtMwjSafAQIjLoeWqPFzwRFM99ykUFyZKkHmii0qlJiqptaCVQbzVfBaZnJZgoozbiFHB/HvqMaUorKR6av6LtSvBUpxcVE6AdaMqs/ADpLXTkN592LubCNTdjLA5TDSAqt3i4WMucm5hKyYRFdTO/29EhG2SW1uaL/b2LMy6xiI3zFhO1QS6rJB7P1VgvL/MXv/zg6P9oz0DkqMNE3Sd7Fxwm3d8Eh2uOgmaFfQi7sHh7vIRxr6gFM3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBmhlVqRwHGsQdLbGFrj4ponORv2x8xvnDdDY5ZPRkCpfXA0KLjABSVXq4oxKLuYpZLQStnaxydb9pklM5l1Rh+1NMYM7COlxr3sUMclRFG0h0PIoYGcm8xTNJJE7VnbmqQZLsDP3z/BbOxjX20k9AvzINAznMinEY0zJLVlM7b579rR2yktIXjtZO47LjYdgrwvGgXQbkqwgKw0PGFYJbqet/JZeL7CtMHz8zJdkLTDqN8rnklntjLgU8cFLtHuCkb4GVJQ5rS+X+uOTraqnEwGc5Z1l7a+bwY02eLw0zwfpaTZ3WQ75RKJSvHSVp3NxIl28HK+v2EI+xeM1vQ6xmqibEvfjWUL1GZovzpNi5uJX/r8dxrmuBJAc+CS3eLoeHpSWtMkoB0KZraggCAvjKZ4Qve7+AczaZN3a5BFeDVQxIAnYC/x+fSxBMWIWZQyXUu2QkAVBp9ftg2yv0cO80FgdriakUARNRQRklhiegkds5LXbr/8lwQvgwf+S6EUmC5baVwGvkf72pXG183y/28flfb+/O/hqdaHcCj4JPg0+C/rBYTAIvglOgtOABS74Ofgl+LX1W+uP1p+tv5ahN2+sMHeCRmv9/Q/4S4tY</latexit>
2. N = {a, c}.<latexit sha1_base64="UnWGOPG7NpsLB9xNGGE4KhYy81s=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+8/F+N/6S3PuWHJPY0YiwuL7XDc93dnvd3qKRq53+qrMbrNrJ+e3WnTgtWCVBWSaoMWf9XmnHjmrLmYA6jCsDJWVTOoEz7CoqwYzdYv01aeNISrJC409ZshgNNyHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsSXhaRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMoLkyUIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuEHSGunIb37sHc3Eai7GWFzmGgAVbvFw8dc5NzCVkwiKqid/9+ICNskt7Y0X+ztWZh1jUVumLGcqgl0WSH3fqrAeH+Zvf7nB0f7R3sGJEcbJug62bngNu/4JDpcdRI0K+hF3IPD3eUjjH1BKZrZ1yeMJ6JIqIjxNfawAShTaRikhUADDNDKrEjhONYg6GyNLXDxTROdjfpj5zfOG6CxyyejIVW+uBoUXGACkqrUxRmVXMxTyGglbO1ik637TZOYzLuiDtubYgZ3ENLjXvcoYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGfun+G3djCut5N6BPiRaRjOZVKIx5iSW7KY2n337GntlJeQvHaydhyXGw/BXheMA+k2JFlBVhoeMKwS3E5b+S29XmBbYfj4mS/JWmDUb5TPJbPaGXEp4oOXaPcEI30NqChzWl8u9ccnW1VPJwI4yzvL2l83gxtt8Hhpng/S02zushzyiUSleOkqT+fiRLp4OV5fsYV8isdreh1iNVE3Je7Hs4TqMzRfnCfFzMWv/H87jHNdCSA58Elu8XQ9PCgtaZNRDoQyW1FBEBbGUzwhet39A5i1ybq1ySO8GqhiQBKwF/j9+liCYsQsyhgupdohIQuCTq/bB9leo4d5obE6XE1IoQiaigjILDE8BY/YyGu3X/9LghfAg/8l0YtMFiy1rwJeI/3tS+Nq5/l+t4/L+35/d/DV6kK5FXwSfBp8FvSDw2AQfBOcBKcBC1zwc/BL8Gvrt9YfrT9bfy1Db95YYe4Ejdb6+x//JYtZ</latexit><latexit sha1_base64="UnWGOPG7NpsLB9xNGGE4KhYy81s=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+8/F+N/6S3PuWHJPY0YiwuL7XDc93dnvd3qKRq53+qrMbrNrJ+e3WnTgtWCVBWSaoMWf9XmnHjmrLmYA6jCsDJWVTOoEz7CoqwYzdYv01aeNISrJC409ZshgNNyHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsSXhaRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMoLkyUIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuEHSGunIb37sHc3Eai7GWFzmGgAVbvFw8dc5NzCVkwiKqid/9+ICNskt7Y0X+ztWZh1jUVumLGcqgl0WSH3fqrAeH+Zvf7nB0f7R3sGJEcbJug62bngNu/4JDpcdRI0K+hF3IPD3eUjjH1BKZrZ1yeMJ6JIqIjxNfawAShTaRikhUADDNDKrEjhONYg6GyNLXDxTROdjfpj5zfOG6CxyyejIVW+uBoUXGACkqrUxRmVXMxTyGglbO1ik637TZOYzLuiDtubYgZ3ENLjXvcoYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGfun+G3djCut5N6BPiRaRjOZVKIx5iSW7KY2n337GntlJeQvHaydhyXGw/BXheMA+k2JFlBVhoeMKwS3E5b+S29XmBbYfj4mS/JWmDUb5TPJbPaGXEp4oOXaPcEI30NqChzWl8u9ccnW1VPJwI4yzvL2l83gxtt8Hhpng/S02zushzyiUSleOkqT+fiRLp4OV5fsYV8isdreh1iNVE3Je7Hs4TqMzRfnCfFzMWv/H87jHNdCSA58Elu8XQ9PCgtaZNRDoQyW1FBEBbGUzwhet39A5i1ybq1ySO8GqhiQBKwF/j9+liCYsQsyhgupdohIQuCTq/bB9leo4d5obE6XE1IoQiaigjILDE8BY/YyGu3X/9LghfAg/8l0YtMFiy1rwJeI/3tS+Nq5/l+t4/L+35/d/DV6kK5FXwSfBp8FvSDw2AQfBOcBKcBC1zwc/BL8Gvrt9YfrT9bfy1Db95YYe4Ejdb6+x//JYtZ</latexit><latexit sha1_base64="UnWGOPG7NpsLB9xNGGE4KhYy81s=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+8/F+N/6S3PuWHJPY0YiwuL7XDc93dnvd3qKRq53+qrMbrNrJ+e3WnTgtWCVBWSaoMWf9XmnHjmrLmYA6jCsDJWVTOoEz7CoqwYzdYv01aeNISrJC409ZshgNNyHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsSXhaRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMoLkyUIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuEHSGunIb37sHc3Eai7GWFzmGgAVbvFw8dc5NzCVkwiKqid/9+ICNskt7Y0X+ztWZh1jUVumLGcqgl0WSH3fqrAeH+Zvf7nB0f7R3sGJEcbJug62bngNu/4JDpcdRI0K+hF3IPD3eUjjH1BKZrZ1yeMJ6JIqIjxNfawAShTaRikhUADDNDKrEjhONYg6GyNLXDxTROdjfpj5zfOG6CxyyejIVW+uBoUXGACkqrUxRmVXMxTyGglbO1ik637TZOYzLuiDtubYgZ3ENLjXvcoYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGfun+G3djCut5N6BPiRaRjOZVKIx5iSW7KY2n337GntlJeQvHaydhyXGw/BXheMA+k2JFlBVhoeMKwS3E5b+S29XmBbYfj4mS/JWmDUb5TPJbPaGXEp4oOXaPcEI30NqChzWl8u9ccnW1VPJwI4yzvL2l83gxtt8Hhpng/S02zushzyiUSleOkqT+fiRLp4OV5fsYV8isdreh1iNVE3Je7Hs4TqMzRfnCfFzMWv/H87jHNdCSA58Elu8XQ9PCgtaZNRDoQyW1FBEBbGUzwhet39A5i1ybq1ySO8GqhiQBKwF/j9+liCYsQsyhgupdohIQuCTq/bB9leo4d5obE6XE1IoQiaigjILDE8BY/YyGu3X/9LghfAg/8l0YtMFiy1rwJeI/3tS+Nq5/l+t4/L+35/d/DV6kK5FXwSfBp8FvSDw2AQfBOcBKcBC1zwc/BL8Gvrt9YfrT9bfy1Db95YYe4Ejdb6+x//JYtZ</latexit><latexit sha1_base64="UnWGOPG7NpsLB9xNGGE4KhYy81s=">AAAHQHicfVVdjxs1FJ0WCGX42lLxxIvLNhKqJtlkq2W7oJUiqCoqtbCQbFtpJ1o8njsZK7ZnsD3dpNb8GF7hX/Av+Ae8IV554jofbCa7YCkZj33POb7XZ+ykFNzYXu/3GzffePOt1tu33gnffe/9Dz7cuf3Rc1NUmsEpK0ShXybUgOAKTi23Al6WGqhMBLxIpl/7+RevQBteqJGdlzCWdKJ4xhm1OHS+8/F+N/6S3PuWHJPY0YiwuL7XDc93dnvd3qKRq53+qrMbrNrJ+e3WnTgtWCVBWSaoMWf9XmnHjmrLmYA6jCsDJWVTOoEz7CoqwYzdYv01aeNISrJC409ZshgNNyHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsSXhaRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMoLkyUIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuEHSGunIb37sHc3Eai7GWFzmGgAVbvFw8dc5NzCVkwiKqid/9+ICNskt7Y0X+ztWZh1jUVumLGcqgl0WSH3fqrAeH+Zvf7nB0f7R3sGJEcbJug62bngNu/4JDpcdRI0K+hF3IPD3eUjjH1BKZrZ1yeMJ6JIqIjxNfawAShTaRikhUADDNDKrEjhONYg6GyNLXDxTROdjfpj5zfOG6CxyyejIVW+uBoUXGACkqrUxRmVXMxTyGglbO1ik637TZOYzLuiDtubYgZ3ENLjXvcoYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGfun+G3djCut5N6BPiRaRjOZVKIx5iSW7KY2n337GntlJeQvHaydhyXGw/BXheMA+k2JFlBVhoeMKwS3E5b+S29XmBbYfj4mS/JWmDUb5TPJbPaGXEp4oOXaPcEI30NqChzWl8u9ccnW1VPJwI4yzvL2l83gxtt8Hhpng/S02zushzyiUSleOkqT+fiRLp4OV5fsYV8isdreh1iNVE3Je7Hs4TqMzRfnCfFzMWv/H87jHNdCSA58Elu8XQ9PCgtaZNRDoQyW1FBEBbGUzwhet39A5i1ybq1ySO8GqhiQBKwF/j9+liCYsQsyhgupdohIQuCTq/bB9leo4d5obE6XE1IoQiaigjILDE8BY/YyGu3X/9LghfAg/8l0YtMFiy1rwJeI/3tS+Nq5/l+t4/L+35/d/DV6kK5FXwSfBp8FvSDw2AQfBOcBKcBC1zwc/BL8Gvrt9YfrT9bfy1Db95YYe4Ejdb6+x//JYtZ</latexit>
3. N = {a, c, b}.<latexit sha1_base64="mSDh8p6Sw4A+jd6Q91R/Xl/FxcY=">AAAHQ3icfVVdjxs1FJ0WCGX46Ja+IPHiso2Eqkk22dWyXdBKEVQVlVpYSLattBMtHs+djBXbM9ieblJr+DW8wr/gR/AbeEO8InGdZNlMdsFSMh77nnN8r8/YSSm4sb3e7zduvvHmW623b70Tvvve+x/c3rrz4XNTVJrBCStEoV8m1IDgCk4stwJelhqoTAS8SKZf+fkXr0AbXqiRnZcwlnSieMYZtTh0tvXRXjf+gtz/hhyR2NGIsIgkcX2/G55tbfe6vUUjVzv9VWc7WLXjszutu3FasEqCskxQY077vdKOHdWWMwF1GFcGSsqmdAKn2FVUghm7RQo1aeNISrJC409ZshgN1yHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsRXhqRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMozk2UIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuF7SGunIb33sHcvEai7HmFzmGgAVbvFw8ec59zCRkwiKqid/1+LCNskt7Y0n+/sWJh1jUVumLGcqgl0WSF3fqzAeIuZnf5n+4e7hzsGJEcnJmg82TnnNu/4JDpcdRL0K+hF3N7B9vIRxr6gFP3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBuhmVqRwFGsQdHaBLXDxTROdjvpj5zfOG6Cxy8ejIVW+uBoUnGMCkqrUxRmVXMxTyGglbO1ik130myYxmXdFHbbXxQzuIKRHve5hxCRHUbSFQMujgJ2ZzFM0k0TuWNmZpxoswc48OMVvbX9cbyb1CPAj0zCcy6QQjzElt2Qxtfv22dPaKS8hee1k7TguNx6CvS4YB9JNSLKCrDQ8YFgluJ228lt6vcCmwvDxM1+SC4FRv1E+l8xqZ8SliA9eot0TjPQ1oKLMaX251B+ebFQ9nQjgLO8sa3/dDG60weOleT5IT7O+y3LIJxKV4qWrPJ2LE+ni5Xh9xRbyKZ6w6XWI1UTdlHgQzxKqT9F8cZ4UMxe/8v/tMM51JYDkwCe5xdP1YL+0pE1GORDKbEUFQVgYT/GE6HV392HWJhetTR7h7UAVA5KAPcfv18cSFCNmUcZwKdUOCVkQdHrdPsj2BXqYFxqrw9WEFIqgqYiAzBLDU/CItby2+/W/JHgB7P0viV5ksmCpfRXwGulvXhpXO893u31c3ne724MvVxfKreDj4JPg06AfHASD4OvgODgJWPBT8HPwS/Br67fWH60/W38tQ2/eWGHuBo3W+vsfL+KMJg==</latexit><latexit sha1_base64="mSDh8p6Sw4A+jd6Q91R/Xl/FxcY=">AAAHQ3icfVVdjxs1FJ0WCGX46Ja+IPHiso2Eqkk22dWyXdBKEVQVlVpYSLattBMtHs+djBXbM9ieblJr+DW8wr/gR/AbeEO8InGdZNlMdsFSMh77nnN8r8/YSSm4sb3e7zduvvHmW623b70Tvvve+x/c3rrz4XNTVJrBCStEoV8m1IDgCk4stwJelhqoTAS8SKZf+fkXr0AbXqiRnZcwlnSieMYZtTh0tvXRXjf+gtz/hhyR2NGIsIgkcX2/G55tbfe6vUUjVzv9VWc7WLXjszutu3FasEqCskxQY077vdKOHdWWMwF1GFcGSsqmdAKn2FVUghm7RQo1aeNISrJC409ZshgN1yHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsRXhqRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMozk2UIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuF7SGunIb33sHcvEai7HmFzmGgAVbvFw8ec59zCRkwiKqid/1+LCNskt7Y0n+/sWJh1jUVumLGcqgl0WSF3fqzAeIuZnf5n+4e7hzsGJEcnJmg82TnnNu/4JDpcdRL0K+hF3N7B9vIRxr6gFP3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBuhmVqRwFGsQdHaBLXDxTROdjvpj5zfOG6Cxy8ejIVW+uBoUnGMCkqrUxRmVXMxTyGglbO1ik130myYxmXdFHbbXxQzuIKRHve5hxCRHUbSFQMujgJ2ZzFM0k0TuWNmZpxoswc48OMVvbX9cbyb1CPAj0zCcy6QQjzElt2Qxtfv22dPaKS8hee1k7TguNx6CvS4YB9JNSLKCrDQ8YFgluJ228lt6vcCmwvDxM1+SC4FRv1E+l8xqZ8SliA9eot0TjPQ1oKLMaX251B+ebFQ9nQjgLO8sa3/dDG60weOleT5IT7O+y3LIJxKV4qWrPJ2LE+ni5Xh9xRbyKZ6w6XWI1UTdlHgQzxKqT9F8cZ4UMxe/8v/tMM51JYDkwCe5xdP1YL+0pE1GORDKbEUFQVgYT/GE6HV392HWJhetTR7h7UAVA5KAPcfv18cSFCNmUcZwKdUOCVkQdHrdPsj2BXqYFxqrw9WEFIqgqYiAzBLDU/CItby2+/W/JHgB7P0viV5ksmCpfRXwGulvXhpXO893u31c3ne724MvVxfKreDj4JPg06AfHASD4OvgODgJWPBT8HPwS/Br67fWH60/W38tQ2/eWGHuBo3W+vsfL+KMJg==</latexit><latexit sha1_base64="mSDh8p6Sw4A+jd6Q91R/Xl/FxcY=">AAAHQ3icfVVdjxs1FJ0WCGX46Ja+IPHiso2Eqkk22dWyXdBKEVQVlVpYSLattBMtHs+djBXbM9ieblJr+DW8wr/gR/AbeEO8InGdZNlMdsFSMh77nnN8r8/YSSm4sb3e7zduvvHmW623b70Tvvve+x/c3rrz4XNTVJrBCStEoV8m1IDgCk4stwJelhqoTAS8SKZf+fkXr0AbXqiRnZcwlnSieMYZtTh0tvXRXjf+gtz/hhyR2NGIsIgkcX2/G55tbfe6vUUjVzv9VWc7WLXjszutu3FasEqCskxQY077vdKOHdWWMwF1GFcGSsqmdAKn2FVUghm7RQo1aeNISrJC409ZshgN1yHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsRXhqRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMozk2UIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuF7SGunIb33sHcvEai7HmFzmGgAVbvFw8ec59zCRkwiKqid/1+LCNskt7Y0n+/sWJh1jUVumLGcqgl0WSF3fqzAeIuZnf5n+4e7hzsGJEcnJmg82TnnNu/4JDpcdRL0K+hF3N7B9vIRxr6gFP3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBuhmVqRwFGsQdHaBLXDxTROdjvpj5zfOG6Cxy8ejIVW+uBoUnGMCkqrUxRmVXMxTyGglbO1ik130myYxmXdFHbbXxQzuIKRHve5hxCRHUbSFQMujgJ2ZzFM0k0TuWNmZpxoswc48OMVvbX9cbyb1CPAj0zCcy6QQjzElt2Qxtfv22dPaKS8hee1k7TguNx6CvS4YB9JNSLKCrDQ8YFgluJ228lt6vcCmwvDxM1+SC4FRv1E+l8xqZ8SliA9eot0TjPQ1oKLMaX251B+ebFQ9nQjgLO8sa3/dDG60weOleT5IT7O+y3LIJxKV4qWrPJ2LE+ni5Xh9xRbyKZ6w6XWI1UTdlHgQzxKqT9F8cZ4UMxe/8v/tMM51JYDkwCe5xdP1YL+0pE1GORDKbEUFQVgYT/GE6HV392HWJhetTR7h7UAVA5KAPcfv18cSFCNmUcZwKdUOCVkQdHrdPsj2BXqYFxqrw9WEFIqgqYiAzBLDU/CItby2+/W/JHgB7P0viV5ksmCpfRXwGulvXhpXO893u31c3ne724MvVxfKreDj4JPg06AfHASD4OvgODgJWPBT8HPwS/Br67fWH60/W38tQ2/eWGHuBo3W+vsfL+KMJg==</latexit><latexit sha1_base64="mSDh8p6Sw4A+jd6Q91R/Xl/FxcY=">AAAHQ3icfVVdjxs1FJ0WCGX46Ja+IPHiso2Eqkk22dWyXdBKEVQVlVpYSLattBMtHs+djBXbM9ieblJr+DW8wr/gR/AbeEO8InGdZNlMdsFSMh77nnN8r8/YSSm4sb3e7zduvvHmW623b70Tvvve+x/c3rrz4XNTVJrBCStEoV8m1IDgCk4stwJelhqoTAS8SKZf+fkXr0AbXqiRnZcwlnSieMYZtTh0tvXRXjf+gtz/hhyR2NGIsIgkcX2/G55tbfe6vUUjVzv9VWc7WLXjszutu3FasEqCskxQY077vdKOHdWWMwF1GFcGSsqmdAKn2FVUghm7RQo1aeNISrJC409ZshgN1yHIo+m8weIsTSpB9aw5mhTFFGdMHYZNTZs9HDuuysqCYkvJrBLEFsRXhqRcA7NiTpq6lk9fR4ozyDRlEZVGUptHJffrjOz0dWeiaZlHkk6BgRCXQ8tVebjgiaZ67lMozk2UIPNEF5VKTVRSa0Erg3ir+SwyOS3BRBm3EaOC+ffUY0pRWEn11PwXa1eCpTi5qJwA60ZVZuF7SGunIb33sHcvEai7HmFzmGgAVbvFw8ec59zCRkwiKqid/1+LCNskt7Y0n+/sWJh1jUVumLGcqgl0WSF3fqzAeIuZnf5n+4e7hzsGJEcnJmg82TnnNu/4JDpcdRL0K+hF3N7B9vIRxr6gFP3s6xPGE1EkVMT4GnvYAJSpNAzSQqABBuhmVqRwFGsQdHaBLXDxTROdjvpj5zfOG6Cxy8ejIVW+uBoUnGMCkqrUxRmVXMxTyGglbO1ik130myYxmXdFHbbXxQzuIKRHve5hxCRHUbSFQMujgJ2ZzFM0k0TuWNmZpxoswc48OMVvbX9cbyb1CPAj0zCcy6QQjzElt2Qxtfv22dPaKS8hee1k7TguNx6CvS4YB9JNSLKCrDQ8YFgluJ228lt6vcCmwvDxM1+SC4FRv1E+l8xqZ8SliA9eot0TjPQ1oKLMaX251B+ebFQ9nQjgLO8sa3/dDG60weOleT5IT7O+y3LIJxKV4qWrPJ2LE+ni5Xh9xRbyKZ6w6XWI1UTdlHgQzxKqT9F8cZ4UMxe/8v/tMM51JYDkwCe5xdP1YL+0pE1GORDKbEUFQVgYT/GE6HV392HWJhetTR7h7UAVA5KAPcfv18cSFCNmUcZwKdUOCVkQdHrdPsj2BXqYFxqrw9WEFIqgqYiAzBLDU/CItby2+/W/JHgB7P0viV5ksmCpfRXwGulvXhpXO893u31c3ne724MvVxfKreDj4JPg06AfHASD4OvgODgJWPBT8HPwS/Br67fWH60/W38tQ2/eWGHuBo3W+vsfL+KMJg==</latexit>
0. N = ;.<latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit><latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit><latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit><latexit sha1_base64="koOJt4XUWyg16qZo3FixiqcvPXI=">AAAHQXicfVVdb9s2FFXbzeu0j6YtsJe9sEsNDIXt2CmyNBsCGFtRrEC7ZbPTFoiMjJKuJMIkpZFUI5fTn9nr9i/2K/YT9jbsdS+7tJzFcrIRsEWR95zDe3lEhgVn2gyHv1+7fuOttzvv3HzXf+/9Dz68tXX7zgudlyqC4yjnuXoVUg2cSTg2zHB4VSigIuTwMpx/5eZfvgalWS6nZlHATNBUsoRF1ODQ6dZHw0HwBbn/DTkkAYjCLDSY+wP/dGt7OBguG7ncGa06296qHZ3e7twN4jwqBUgTcar1yWhYmJmlyrCIQ+0HpYaCRnOawgl2JRWgZ3aZQE26OBKTJFf4k4YsR/11CPIoumixWEPDklNVtUfDPJ/jjK59v61pkkczy2RRGpBRI5mUnJicuLqQmCmIDF+Qtq5h8zc9ySJIFI16VGhBTdYrmFtnz8zf9FNFi6wn6Bwi4PxiqFmVg3MWKqoWLoX8TPdCZE5VXspY9wpqDCipEW8Uq3o6owXoXsJML6I8cu+xwxQ8N4Kquf4v1oEAQ3FyWTkOxk7LxMD3ENdWQXzv0fBeyFF3PcJkkCoAWdvlw8WcZczARkzIS6it+1+L8LskM6bQn+/sGKgG2iA3VFFGZQqDKBc7P5agncH0zuizvYPdgx0NgqEPQ7Sd6J8xk/VdEn0m+yG6FdQy7uH+dvPwA1dQim529fGDlOch5QG+Bg42BqlLBeM452iAMXo5ymM4DBRwWp1jc1x820Qn09HMuo1zBmjt8tF0QqUrrgIJZ5iAoDK2QUIF44sYElpyU9tAJ+f9tkl04lxR+911MY07CPHhcHDQiwRDUbQFR8ujgKl04ijaSSJ3IE3lqMYN2OoHJ/it7c3qzaQeA35kCiYLEeb8CaZkGxZd22+fP6utdBKC1VbUluFygwmYq4JxIN6EhCvISsMBJmWI22lKt6VXC2wqTJ48dyU5F5iOWuWzYVVbzS9EXHCDtk8x0tWA8iKj9cVSf3i6UfU45cCirN/U/qoZ3GiNx0v7fBCOZn2XxYSlApWCxlWOzgahsEEzXl+yhXiG52t8FWI1UbclHgRVSNUJmi/IwryywWv33/WDTJUcSAYszQyervt7hSFdMs2A0MiUlBOE+cEcT4jhYHcPqi45b13yGO8GKiMgIZgz/H5dLEExopdl9Buprk/IkqA/HIxAdM/RkyxXWB0mU5JLgqYiHBJDNIvBIdby2h7V/5LgBfDwf0nUMpMlS+2qgNfIaPPSuNx5sTsY4fK+290ef7m6UG56H3ufeJ96I2/fG3tfe0fesRd5P3k/e794v3Z+6/zR+bPzVxN6/doKc9drtc7f/wCI04x4</latexit>
1. N = {a, c, d}.<latexit sha1_base64="cQc0H4GWbHtVI0fEsTgfVT1qu8Q=">AAAHQ3icfVVdjxs1FJ22EMrw0W37gsSLyzYSqibZZKtlu6CVIqgqKrWwkGxbaSdaPJ47GSu2Z7A93aTW8Gt4hX/Bj+A38IZ4ReI6ybKZ7IKlZDz2Pef4Xp+xk1JwY3u9369dv/HW2613br4bvvf+Bx/e2rp954UpKs3gmBWi0K8SakBwBceWWwGvSg1UJgJeJtOv/PzL16ANL9TIzksYSzpRPOOMWhw63fqo342/IPe/IYckdjQiLCJpXN/vhqdb271ub9HI5U5/1dkOVu3o9HbrbpwWrJKgLBPUmJN+r7RjR7XlTEAdxpWBkrIpncAJdhWVYMZukUJN2jiSkqzQ+FOWLEbDdQjyaDpvsDhLk0pQPWuOJkUxxRlTh2FT02aPxo6rsrKg2FIyqwSxBfGVISnXwKyYk6au5dM3keIMMk1ZRKWR1OZRyf06Izt905loWuaRpFNgIMTF0HJVHi54oqme+xSKMxMlyDzRRaVSE5XUWtDKIN5qPotMTkswUcZtxKhg/j31mFIUVlI9Nf/F2pVgKU4uKifAulGVWfge0tppSO896t1LBOquR9gcJhpA1W7x8DFnObewEZOICmrn/9ciwjbJrS3N5zs7FmZdY5EbZiynagJdVsidHysw3mJmp//Z3sHuwY4BydGJCRpPds64zTs+iQ5XnQT9CnoR93B/e/kIY19Qin729QnjiSgSKmJ8jT1sAMpUGgZpIdAAA3QzK1I4jDUIOjvHFrj4polORv2x8xvnDdDY5aPRkCpfXA0KzjABSVXq4oxKLuYpZLQStnaxyc77TZOYzLuiDtvrYgZ3ENLDXvcgYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGcenOC3tjeuN5N6DPiRaRjOZVKIJ5iSW7KY2n37/FntlJeQvHaydhyXGw/BXhWMA+kmJFlBVhoeMKwS3E5b+S29WmBTYfjkuS/JucCo3yifS2a1M+JCxAcv0e4pRvoaUFHmtL5Y6g9PN6qeTgRwlneWtb9qBjfa4PHSPB+kp1nfZTnkE4lK8dJVns7FiXTxcry+ZAv5DE/Y9CrEaqJuSjyIZwnVJ2i+OE+KmYtf+/92GOe6EkBy4JPc4um6v1da0iajHAhltqKCICyMp3hC9Lq7ezBrk/PWJo/xdqCKAUnAnuH362MJihGzKGO4lGqHhCwIOr1uH2T7HD3MC43V4WpCCkXQVERAZonhKXjEWl7b/fpfErwAHv4viV5ksmCpfRXwGulvXhqXOy92u31c3ne724MvVxfKzeDj4JPg06Af7AeD4OvgKDgOWPBT8HPwS/Br67fWH60/W38tQ69fW2HuBo3W+vsfL76MJg==</latexit><latexit sha1_base64="cQc0H4GWbHtVI0fEsTgfVT1qu8Q=">AAAHQ3icfVVdjxs1FJ22EMrw0W37gsSLyzYSqibZZKtlu6CVIqgqKrWwkGxbaSdaPJ47GSu2Z7A93aTW8Gt4hX/Bj+A38IZ4ReI6ybKZ7IKlZDz2Pef4Xp+xk1JwY3u9369dv/HW2613br4bvvf+Bx/e2rp954UpKs3gmBWi0K8SakBwBceWWwGvSg1UJgJeJtOv/PzL16ANL9TIzksYSzpRPOOMWhw63fqo342/IPe/IYckdjQiLCJpXN/vhqdb271ub9HI5U5/1dkOVu3o9HbrbpwWrJKgLBPUmJN+r7RjR7XlTEAdxpWBkrIpncAJdhWVYMZukUJN2jiSkqzQ+FOWLEbDdQjyaDpvsDhLk0pQPWuOJkUxxRlTh2FT02aPxo6rsrKg2FIyqwSxBfGVISnXwKyYk6au5dM3keIMMk1ZRKWR1OZRyf06Izt905loWuaRpFNgIMTF0HJVHi54oqme+xSKMxMlyDzRRaVSE5XUWtDKIN5qPotMTkswUcZtxKhg/j31mFIUVlI9Nf/F2pVgKU4uKifAulGVWfge0tppSO896t1LBOquR9gcJhpA1W7x8DFnObewEZOICmrn/9ciwjbJrS3N5zs7FmZdY5EbZiynagJdVsidHysw3mJmp//Z3sHuwY4BydGJCRpPds64zTs+iQ5XnQT9CnoR93B/e/kIY19Qin729QnjiSgSKmJ8jT1sAMpUGgZpIdAAA3QzK1I4jDUIOjvHFrj4polORv2x8xvnDdDY5aPRkCpfXA0KzjABSVXq4oxKLuYpZLQStnaxyc77TZOYzLuiDtvrYgZ3ENLDXvcgYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGcenOC3tjeuN5N6DPiRaRjOZVKIJ5iSW7KY2n37/FntlJeQvHaydhyXGw/BXhWMA+kmJFlBVhoeMKwS3E5b+S29WmBTYfjkuS/JucCo3yifS2a1M+JCxAcv0e4pRvoaUFHmtL5Y6g9PN6qeTgRwlneWtb9qBjfa4PHSPB+kp1nfZTnkE4lK8dJVns7FiXTxcry+ZAv5DE/Y9CrEaqJuSjyIZwnVJ2i+OE+KmYtf+/92GOe6EkBy4JPc4um6v1da0iajHAhltqKCICyMp3hC9Lq7ezBrk/PWJo/xdqCKAUnAnuH362MJihGzKGO4lGqHhCwIOr1uH2T7HD3MC43V4WpCCkXQVERAZonhKXjEWl7b/fpfErwAHv4viV5ksmCpfRXwGulvXhqXOy92u31c3ne724MvVxfKzeDj4JPg06Af7AeD4OvgKDgOWPBT8HPwS/Br67fWH60/W38tQ69fW2HuBo3W+vsfL76MJg==</latexit><latexit sha1_base64="cQc0H4GWbHtVI0fEsTgfVT1qu8Q=">AAAHQ3icfVVdjxs1FJ22EMrw0W37gsSLyzYSqibZZKtlu6CVIqgqKrWwkGxbaSdaPJ47GSu2Z7A93aTW8Gt4hX/Bj+A38IZ4ReI6ybKZ7IKlZDz2Pef4Xp+xk1JwY3u9369dv/HW2613br4bvvf+Bx/e2rp954UpKs3gmBWi0K8SakBwBceWWwGvSg1UJgJeJtOv/PzL16ANL9TIzksYSzpRPOOMWhw63fqo342/IPe/IYckdjQiLCJpXN/vhqdb271ub9HI5U5/1dkOVu3o9HbrbpwWrJKgLBPUmJN+r7RjR7XlTEAdxpWBkrIpncAJdhWVYMZukUJN2jiSkqzQ+FOWLEbDdQjyaDpvsDhLk0pQPWuOJkUxxRlTh2FT02aPxo6rsrKg2FIyqwSxBfGVISnXwKyYk6au5dM3keIMMk1ZRKWR1OZRyf06Izt905loWuaRpFNgIMTF0HJVHi54oqme+xSKMxMlyDzRRaVSE5XUWtDKIN5qPotMTkswUcZtxKhg/j31mFIUVlI9Nf/F2pVgKU4uKifAulGVWfge0tppSO896t1LBOquR9gcJhpA1W7x8DFnObewEZOICmrn/9ciwjbJrS3N5zs7FmZdY5EbZiynagJdVsidHysw3mJmp//Z3sHuwY4BydGJCRpPds64zTs+iQ5XnQT9CnoR93B/e/kIY19Qin729QnjiSgSKmJ8jT1sAMpUGgZpIdAAA3QzK1I4jDUIOjvHFrj4polORv2x8xvnDdDY5aPRkCpfXA0KzjABSVXq4oxKLuYpZLQStnaxyc77TZOYzLuiDtvrYgZ3ENLDXvcgYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGcenOC3tjeuN5N6DPiRaRjOZVKIJ5iSW7KY2n37/FntlJeQvHaydhyXGw/BXhWMA+kmJFlBVhoeMKwS3E5b+S29WmBTYfjkuS/JucCo3yifS2a1M+JCxAcv0e4pRvoaUFHmtL5Y6g9PN6qeTgRwlneWtb9qBjfa4PHSPB+kp1nfZTnkE4lK8dJVns7FiXTxcry+ZAv5DE/Y9CrEaqJuSjyIZwnVJ2i+OE+KmYtf+/92GOe6EkBy4JPc4um6v1da0iajHAhltqKCICyMp3hC9Lq7ezBrk/PWJo/xdqCKAUnAnuH362MJihGzKGO4lGqHhCwIOr1uH2T7HD3MC43V4WpCCkXQVERAZonhKXjEWl7b/fpfErwAHv4viV5ksmCpfRXwGulvXhqXOy92u31c3ne724MvVxfKzeDj4JPg06Af7AeD4OvgKDgOWPBT8HPwS/Br67fWH60/W38tQ69fW2HuBo3W+vsfL76MJg==</latexit><latexit sha1_base64="cQc0H4GWbHtVI0fEsTgfVT1qu8Q=">AAAHQ3icfVVdjxs1FJ22EMrw0W37gsSLyzYSqibZZKtlu6CVIqgqKrWwkGxbaSdaPJ47GSu2Z7A93aTW8Gt4hX/Bj+A38IZ4ReI6ybKZ7IKlZDz2Pef4Xp+xk1JwY3u9369dv/HW2613br4bvvf+Bx/e2rp954UpKs3gmBWi0K8SakBwBceWWwGvSg1UJgJeJtOv/PzL16ANL9TIzksYSzpRPOOMWhw63fqo342/IPe/IYckdjQiLCJpXN/vhqdb271ub9HI5U5/1dkOVu3o9HbrbpwWrJKgLBPUmJN+r7RjR7XlTEAdxpWBkrIpncAJdhWVYMZukUJN2jiSkqzQ+FOWLEbDdQjyaDpvsDhLk0pQPWuOJkUxxRlTh2FT02aPxo6rsrKg2FIyqwSxBfGVISnXwKyYk6au5dM3keIMMk1ZRKWR1OZRyf06Izt905loWuaRpFNgIMTF0HJVHi54oqme+xSKMxMlyDzRRaVSE5XUWtDKIN5qPotMTkswUcZtxKhg/j31mFIUVlI9Nf/F2pVgKU4uKifAulGVWfge0tppSO896t1LBOquR9gcJhpA1W7x8DFnObewEZOICmrn/9ciwjbJrS3N5zs7FmZdY5EbZiynagJdVsidHysw3mJmp//Z3sHuwY4BydGJCRpPds64zTs+iQ5XnQT9CnoR93B/e/kIY19Qin729QnjiSgSKmJ8jT1sAMpUGgZpIdAAA3QzK1I4jDUIOjvHFrj4polORv2x8xvnDdDY5aPRkCpfXA0KzjABSVXq4oxKLuYpZLQStnaxyc77TZOYzLuiDtvrYgZ3ENLDXvcgYpKjKNpCoOVRwM5M5imaSSJ3rOzMUw2WYGcenOC3tjeuN5N6DPiRaRjOZVKIJ5iSW7KY2n37/FntlJeQvHaydhyXGw/BXhWMA+kmJFlBVhoeMKwS3E5b+S29WmBTYfjkuS/JucCo3yifS2a1M+JCxAcv0e4pRvoaUFHmtL5Y6g9PN6qeTgRwlneWtb9qBjfa4PHSPB+kp1nfZTnkE4lK8dJVns7FiXTxcry+ZAv5DE/Y9CrEaqJuSjyIZwnVJ2i+OE+KmYtf+/92GOe6EkBy4JPc4um6v1da0iajHAhltqKCICyMp3hC9Lq7ezBrk/PWJo/xdqCKAUnAnuH362MJihGzKGO4lGqHhCwIOr1uH2T7HD3MC43V4WpCCkXQVERAZonhKXjEWl7b/fpfErwAHv4viV5ksmCpfRXwGulvXhqXOy92u31c3ne724MvVxfKzeDj4JPg06Af7AeD4OvgKDgOWPBT8HPwS/Br67fWH60/W38tQ69fW2HuBo3W+vsfL76MJg==</latexit>
0.8·0.8·0.8
0.8·0.8·0.2
0.8 + 0.2
0.2·0.8 + 0.8·0.8

17. We can learn model parameters with maximum
likelihood estimation.
17
1. Fix correlation probability p and learn recency weights w.
⟶ single p, vector w learned for entire dataset.
2. Grid search over p, gradient descent on w.
⟶ structure of CRU model makes it easy to compute gradients.

18. The optimal correlation probability is consistent within
domain but differs between domains.
18
Meanper-setlikelihood
x Baseline model (flat, no structure). Similar to [Anderson+ 14]
CRU model.

19. Learned weights tend to decrease monotonically,
which agrees with recency bias in the data.
19
100
101
102
index
10 3
10 2
10 1
Recencyweightw
contact-prim-school
100
101
102
index
10 3
10 2
Recencyweightw
email-Eu-core
100
101
102
index
10 3
10 2
Recencyweightw
coauth-Geology
100
101
102
index
10 2
Recencyweightw
tags-mathoverflow
Correlation
probability p.

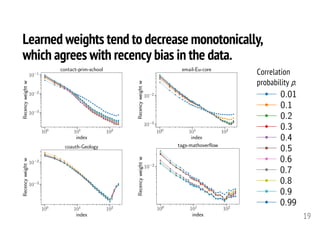
20. Asymptotic behavior depends on the
recency weight model parameters.
20
Theorem.
Let Wj =
Pj
i=1 wi.
If W1 < 1, the model tips with probability 1.
If W1 = 1, then every pair occurs infinitely often.<latexit sha1_base64="aOBbWA3HiGqepuD2cTVGzYijJ6s=">AAAH3HicfVXfb9s2ELa7re60H03Xhz3shV1iYChsx0qRpRlmwNiKbAFSLJvdpkDkepR0sjiTlEZStV1Cb3sb9rr/Y3/O/psdbWexnGwCbFHkfffx7r4jw5wzbbrdv+t33nn3vbuNe+97H3z40cf3dx588lJnhYrgRZTxTL0KqQbOJLwwzHB4lSugIuRwEU6/desXb0BplsmhWeQwEnQiWcIianBqvPNXIDMmY5CGnIEhexdj+0tJeiTQhRhb1vPL1zgxG7O9DgkC7zRZmgRMJmZRkq/JarTXIiYFIrIYODEs12TGTEpylYU0ZJyZBfFvw/cqeEkAt7ogOWWKZFFUKE1wmUlmgC9IlhiQHW+8s9vtdJcPuTnw14Pd2vo5Hz+4+zCIs6gQGGTEqdaXfjc3I0uVYRGH0gsKDTmNpnQClziUVIAe2WVuS9LEmZgkmcIfJmk5621C0I+ii4oXa2hYcKrm1dkwy6a4okvPq3Ka5OnIMpkXGGC0okwKTGRGXMlIzBREBjNQ5TVs+rYlWQSJolGLCi2oSVs5c/tsmenb9kTRPG0JOoUIOL+eWu3KwTkLFVULF0I2060QPU9UVshYt3JqDCipEW8Um7d0SnPQrYSZVkR55L5jh8l5ZgRVU/1fXjsCDMXFZeY4GDsssJA/QVxaBfGjp91HIUfeTQvUwkQByNIuX85mlqIItmxCXkBp3f+GhdckqTG5/mp/38C8ow36hnmUUjmBTpSJ/V8L0E77et//8vD44Hhfg2CouxA7QrSdbtsuiDaT7RAbCdTS7snR7urlBS6hFBvN5ccLJhw1zgP8DBysD1IXCvpxxlEAfWyzCJuiFyjgdH6FzXDzVRFdDv2RdYVzAqhU+Xw4oNIlV4GEGQYgqIxtkFDB+CKGhBbclDbQydW4KhKdOFWUXnOTTGMFIe51O8etSDAkRVlwlDwSmLlOnItqkOg7kGbuXPVXYKsfX2KvHY7K7aCeATaZgsFChBk/wZDsyosu7Q/Pz0orHYVgpRWlZbjdYADmNmOciLch4Rqy5nCAQRFiOU3hSno7wTbD4OS5S8kVwdCvpM+G89Jqfk3ijFdoe4qWLgeU5yktr7f68+lW1uMJBxal7VXub1vBQms8Xqrng3BuNqssBmwikClYqcq5s0EobLCaL2/IQpzh0R/fhlgvlFWKx8E8pOoSxRekYTa3wRv33/SCVBUcSApskho8XY8Oc0OaZIiHPI1MQTlBmBdM8YTodg4OYd4kV0+TPMNri8oISAhmhv3rbAmSEb1Mo7eianqELB20ux0fRPMKPUgzhdlhckIyubxWOCSGaBaDQ2zEteuX/zrBC+DJ/zpRy0iWXkqXBbxG/O1L4+bg5UHHx+39eLDb/2Z9odyrfVb7vPZFza8d1fq172vntRe1qP5pvVc/qX/XeN34rfF744+V6Z36GvOwVnkaf/4DFizBCg==</latexit><latexit sha1_base64="aOBbWA3HiGqepuD2cTVGzYijJ6s=">AAAH3HicfVXfb9s2ELa7re60H03Xhz3shV1iYChsx0qRpRlmwNiKbAFSLJvdpkDkepR0sjiTlEZStV1Cb3sb9rr/Y3/O/psdbWexnGwCbFHkfffx7r4jw5wzbbrdv+t33nn3vbuNe+97H3z40cf3dx588lJnhYrgRZTxTL0KqQbOJLwwzHB4lSugIuRwEU6/desXb0BplsmhWeQwEnQiWcIianBqvPNXIDMmY5CGnIEhexdj+0tJeiTQhRhb1vPL1zgxG7O9DgkC7zRZmgRMJmZRkq/JarTXIiYFIrIYODEs12TGTEpylYU0ZJyZBfFvw/cqeEkAt7ogOWWKZFFUKE1wmUlmgC9IlhiQHW+8s9vtdJcPuTnw14Pd2vo5Hz+4+zCIs6gQGGTEqdaXfjc3I0uVYRGH0gsKDTmNpnQClziUVIAe2WVuS9LEmZgkmcIfJmk5621C0I+ii4oXa2hYcKrm1dkwy6a4okvPq3Ka5OnIMpkXGGC0okwKTGRGXMlIzBREBjNQ5TVs+rYlWQSJolGLCi2oSVs5c/tsmenb9kTRPG0JOoUIOL+eWu3KwTkLFVULF0I2060QPU9UVshYt3JqDCipEW8Um7d0SnPQrYSZVkR55L5jh8l5ZgRVU/1fXjsCDMXFZeY4GDsssJA/QVxaBfGjp91HIUfeTQvUwkQByNIuX85mlqIItmxCXkBp3f+GhdckqTG5/mp/38C8ow36hnmUUjmBTpSJ/V8L0E77et//8vD44Hhfg2CouxA7QrSdbtsuiDaT7RAbCdTS7snR7urlBS6hFBvN5ccLJhw1zgP8DBysD1IXCvpxxlEAfWyzCJuiFyjgdH6FzXDzVRFdDv2RdYVzAqhU+Xw4oNIlV4GEGQYgqIxtkFDB+CKGhBbclDbQydW4KhKdOFWUXnOTTGMFIe51O8etSDAkRVlwlDwSmLlOnItqkOg7kGbuXPVXYKsfX2KvHY7K7aCeATaZgsFChBk/wZDsyosu7Q/Pz0orHYVgpRWlZbjdYADmNmOciLch4Rqy5nCAQRFiOU3hSno7wTbD4OS5S8kVwdCvpM+G89Jqfk3ijFdoe4qWLgeU5yktr7f68+lW1uMJBxal7VXub1vBQms8Xqrng3BuNqssBmwikClYqcq5s0EobLCaL2/IQpzh0R/fhlgvlFWKx8E8pOoSxRekYTa3wRv33/SCVBUcSApskho8XY8Oc0OaZIiHPI1MQTlBmBdM8YTodg4OYd4kV0+TPMNri8oISAhmhv3rbAmSEb1Mo7eianqELB20ux0fRPMKPUgzhdlhckIyubxWOCSGaBaDQ2zEteuX/zrBC+DJ/zpRy0iWXkqXBbxG/O1L4+bg5UHHx+39eLDb/2Z9odyrfVb7vPZFza8d1fq172vntRe1qP5pvVc/qX/XeN34rfF744+V6Z36GvOwVnkaf/4DFizBCg==</latexit><latexit sha1_base64="aOBbWA3HiGqepuD2cTVGzYijJ6s=">AAAH3HicfVXfb9s2ELa7re60H03Xhz3shV1iYChsx0qRpRlmwNiKbAFSLJvdpkDkepR0sjiTlEZStV1Cb3sb9rr/Y3/O/psdbWexnGwCbFHkfffx7r4jw5wzbbrdv+t33nn3vbuNe+97H3z40cf3dx588lJnhYrgRZTxTL0KqQbOJLwwzHB4lSugIuRwEU6/desXb0BplsmhWeQwEnQiWcIianBqvPNXIDMmY5CGnIEhexdj+0tJeiTQhRhb1vPL1zgxG7O9DgkC7zRZmgRMJmZRkq/JarTXIiYFIrIYODEs12TGTEpylYU0ZJyZBfFvw/cqeEkAt7ogOWWKZFFUKE1wmUlmgC9IlhiQHW+8s9vtdJcPuTnw14Pd2vo5Hz+4+zCIs6gQGGTEqdaXfjc3I0uVYRGH0gsKDTmNpnQClziUVIAe2WVuS9LEmZgkmcIfJmk5621C0I+ii4oXa2hYcKrm1dkwy6a4okvPq3Ka5OnIMpkXGGC0okwKTGRGXMlIzBREBjNQ5TVs+rYlWQSJolGLCi2oSVs5c/tsmenb9kTRPG0JOoUIOL+eWu3KwTkLFVULF0I2060QPU9UVshYt3JqDCipEW8Um7d0SnPQrYSZVkR55L5jh8l5ZgRVU/1fXjsCDMXFZeY4GDsssJA/QVxaBfGjp91HIUfeTQvUwkQByNIuX85mlqIItmxCXkBp3f+GhdckqTG5/mp/38C8ow36hnmUUjmBTpSJ/V8L0E77et//8vD44Hhfg2CouxA7QrSdbtsuiDaT7RAbCdTS7snR7urlBS6hFBvN5ccLJhw1zgP8DBysD1IXCvpxxlEAfWyzCJuiFyjgdH6FzXDzVRFdDv2RdYVzAqhU+Xw4oNIlV4GEGQYgqIxtkFDB+CKGhBbclDbQydW4KhKdOFWUXnOTTGMFIe51O8etSDAkRVlwlDwSmLlOnItqkOg7kGbuXPVXYKsfX2KvHY7K7aCeATaZgsFChBk/wZDsyosu7Q/Pz0orHYVgpRWlZbjdYADmNmOciLch4Rqy5nCAQRFiOU3hSno7wTbD4OS5S8kVwdCvpM+G89Jqfk3ijFdoe4qWLgeU5yktr7f68+lW1uMJBxal7VXub1vBQms8Xqrng3BuNqssBmwikClYqcq5s0EobLCaL2/IQpzh0R/fhlgvlFWKx8E8pOoSxRekYTa3wRv33/SCVBUcSApskho8XY8Oc0OaZIiHPI1MQTlBmBdM8YTodg4OYd4kV0+TPMNri8oISAhmhv3rbAmSEb1Mo7eianqELB20ux0fRPMKPUgzhdlhckIyubxWOCSGaBaDQ2zEteuX/zrBC+DJ/zpRy0iWXkqXBbxG/O1L4+bg5UHHx+39eLDb/2Z9odyrfVb7vPZFza8d1fq172vntRe1qP5pvVc/qX/XeN34rfF744+V6Z36GvOwVnkaf/4DFizBCg==</latexit><latexit sha1_base64="aOBbWA3HiGqepuD2cTVGzYijJ6s=">AAAH3HicfVXfb9s2ELa7re60H03Xhz3shV1iYChsx0qRpRlmwNiKbAFSLJvdpkDkepR0sjiTlEZStV1Cb3sb9rr/Y3/O/psdbWexnGwCbFHkfffx7r4jw5wzbbrdv+t33nn3vbuNe+97H3z40cf3dx588lJnhYrgRZTxTL0KqQbOJLwwzHB4lSugIuRwEU6/desXb0BplsmhWeQwEnQiWcIianBqvPNXIDMmY5CGnIEhexdj+0tJeiTQhRhb1vPL1zgxG7O9DgkC7zRZmgRMJmZRkq/JarTXIiYFIrIYODEs12TGTEpylYU0ZJyZBfFvw/cqeEkAt7ogOWWKZFFUKE1wmUlmgC9IlhiQHW+8s9vtdJcPuTnw14Pd2vo5Hz+4+zCIs6gQGGTEqdaXfjc3I0uVYRGH0gsKDTmNpnQClziUVIAe2WVuS9LEmZgkmcIfJmk5621C0I+ii4oXa2hYcKrm1dkwy6a4okvPq3Ka5OnIMpkXGGC0okwKTGRGXMlIzBREBjNQ5TVs+rYlWQSJolGLCi2oSVs5c/tsmenb9kTRPG0JOoUIOL+eWu3KwTkLFVULF0I2060QPU9UVshYt3JqDCipEW8Um7d0SnPQrYSZVkR55L5jh8l5ZgRVU/1fXjsCDMXFZeY4GDsssJA/QVxaBfGjp91HIUfeTQvUwkQByNIuX85mlqIItmxCXkBp3f+GhdckqTG5/mp/38C8ow36hnmUUjmBTpSJ/V8L0E77et//8vD44Hhfg2CouxA7QrSdbtsuiDaT7RAbCdTS7snR7urlBS6hFBvN5ccLJhw1zgP8DBysD1IXCvpxxlEAfWyzCJuiFyjgdH6FzXDzVRFdDv2RdYVzAqhU+Xw4oNIlV4GEGQYgqIxtkFDB+CKGhBbclDbQydW4KhKdOFWUXnOTTGMFIe51O8etSDAkRVlwlDwSmLlOnItqkOg7kGbuXPVXYKsfX2KvHY7K7aCeATaZgsFChBk/wZDsyosu7Q/Pz0orHYVgpRWlZbjdYADmNmOciLch4Rqy5nCAQRFiOU3hSno7wTbD4OS5S8kVwdCvpM+G89Jqfk3ijFdoe4qWLgeU5yktr7f68+lW1uMJBxal7VXub1vBQms8Xqrng3BuNqssBmwikClYqcq5s0EobLCaL2/IQpzh0R/fhlgvlFWKx8E8pOoSxRekYTa3wRv33/SCVBUcSApskho8XY8Oc0OaZIiHPI1MQTlBmBdM8YTodg4OYd4kV0+TPMNri8oISAhmhv3rbAmSEb1Mo7eianqELB20ux0fRPMKPUgzhdlhckIyubxWOCSGaBaDQ2zEteuX/zrBC+DJ/zpRy0iWXkqXBbxG/O1L4+bg5UHHx+39eLDb/2Z9odyrfVb7vPZFza8d1fq172vntRe1qP5pvVc/qX/XeN34rfF744+V6Z36GvOwVnkaf/4DFizBCg==</latexit>
We say that the model tips if
after some point, only one set appears forever more.
(Similar flavor of result to single-item sequence models [Anderson+ 14].)

21. Recap on Set Prediction #1.
Individuals repeating interactions.
21
1. The data exhibits complex repetition patterns.
2. Correlated Repeated Unions (CRU) is a model for repeat structure.
3. Optimal correlation probabilities are consistent within domain
but different across domains.
4. Optimal weights look the same across domains—fat tails.
5. Can analyze the asymptotic behavior of the model.
{a, b, c}, {a, b}, {c, d, e, f}, {a, c}, {c}, {a, b, c}, {e, g, h}, {h}, …
{a, b}, {a, x}, {a, y}, {a}, {a}, {a}, {z}, {a, b, x, y, z}, …
{j}, {j, k, l}, {a, j}, {a}, {a, k}, {a, j, k, l}, {j, k, l}, {j, k, l}, {j, k}…
Code. bit.ly/SoS-code
Data. bit.ly/SoS-data

22. 22
Set Prediction #2. Subset choice models.
Given a slate of alternatives, how do people choose a subset of the alternatives?
What to buy after browsing Amazon? How to construct a playlist on Spotify?
A discrete choice model for subset selection. Benson, Kumar, & Tomkins. WSDM, 2018.

23. Given some slate of alternatives,
how do people make choices?
23
• If choosing just one thing (buying a car, picking a restaurant, etc.), there
are many good ML techniques (logistic regression, deep nets, etc.)
• If choosing a subset of the alternatives (what to buy after browsing
Amazon, constructing a playlist on Spotify, etc.), there are not many tools.
• We develop a simple and interpretable model for subset selection.

24. Our discrete choice model for subset selection
as illustrated through choosing party snacks.
24
Large set of snack options and want to choose a few.
{tortilla chips, potato chips, cookies, pretzels, guacamole, celery, nut mix, hummus,
meatballs, cupcakes, pigs in blankets, cupcakes, potato skins, chicken wings, taquitos, …}
Model 1.
Independent choices.
Easy computation,
but not realistic.
Model 2.
All subsets as options.
Harder computation, but
more modeling power
Our model.
Some“special subsets”as options +
independent choices.
Interpolate between computation
and modeling power.
healthyfoodtribe.comtoday.com

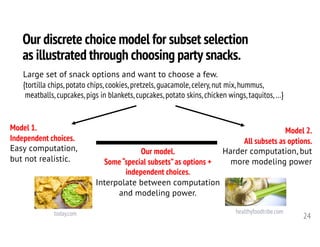
25. Our model is based on a generalization of classical discrete
choice and random utility maximization theory.
25
Discrete Choice Methods with Simulation,Train,2009 (https://eml.berkeley.edu/books/choice2.html)
• Observe choice set C with items 1, …, c. Choose one element.
• Random utility of ith item: Ui = Vi + ei
Vi is base utility, ei is i.i.d. Gumbel distributed error
• If choosing the item with largest random utility…
• (Logistic regression assumes for feature vector x of sample)
Pr[select item i | C] = eVi
P
j2C e
Vj
<latexit sha1_base64="MHw/TabkLT3RqXx2r462XmZzKDE=">AAAHeHicfVVdb9s2FFW7Lem0j6br417Yxca2wnbsFFmaFQGMpShWoMGy2U0LmF5GSVcWa5LSSKqxS+hX7df0dfsXe9ql7SyRk42AJOrynnt4Lw/JqBDc2G73/a3bH3z40cbmnY/DTz797PO7W/e+ODV5qWN4Geci168jZkBwBS8ttwJeFxqYjAS8iqZHfvzVW9CG52po5wWMJZsonvKYWTSdbR2f6BGiIbaEW5CkwRukQZ9QxFj6BPtHjTFpHBKaahY7+NWdnvGqctSU8sy9IZQrclQtzG+qqnG2td3tdBeNXO/0Vp3tYNVOzu5t3KdJHpcSlI0FM2bU6xZ27Ji2PBZQhbQ0ULB4yiYwwq5iEszYLfKuSBMtCUlzjY+yZGENr0IwjmbzWhRnWVQKpmd1a5TnUxwxVRjWOW36eOy4KkoLKl5SpqUgNie+nCThGmsn5qTOa/n0XUvxGHzZWkwayWzWKrifZ8tO37UnmhVZS7IpxCDEpWk5Kw8XPNJMz30K+blpRRh5ovNSJaZVMGtBK4N4q/msZTJWgGml3LZiJmL/n3hMIXIrmZ6a/4rakWAZDi4qJ8C6YZla+AWSymlIHjzuPogE8l71sBlMNICq3OLjfc4zlM6aTyRKqJx/X/EImySztjDf7+xYmHWMxdgwizOmJtCJc7nzewnG69Ls9L7bO9g92DEgOUoxQrXK9jm3Wdsn0eaqHaHIQS/8Hu1vLz8h9QVluAl8fUI6EXnEBMVf6mF9UKbU0E9ygQLo4xaI8wQOqQbBZhfYHCdfF9Fo2Bs7v3BeALVVPhkOmPLF1aDgHBOQTCWOpkxyMU8gZaWwfq+kF/26SEzqVVGFzatkBlcQksNu56AVS46kKAuBkkcCOzOpD1FPEmNTZWc+VH8JdubhCPfa3rhaT+op4CbTMJjLKBfPMCW3jGIq99Pxi8opTyF55WTlOE6XDsDe5IyGZB0SrSArDg8YlBEupy39kt5MsM4weHbsS3JBMOzVyueiWeWMuCTxzku0e46evgZMFBmrLqf62/O1qicTATzO2sva3zSCC23weKmfD9KHubrKcsAnEpnoUlU+nKORdHRpr67JQr7AYzm5CbEaqOoUD+ksYnqE4qNZlM8cfevfzZBmuhRAMuCTzOLpur9XWNIkwwwIi23JBEFYSKd4QnQ7u3swa5KL1iRP8UphKgYSgT3H/et9CZIRsyhjuKRqhoQsArS7nR7I5gV6kOUaq8PVhOSKoKiIgNQSwxPwiCt5bfeqf4PgBfDof4PoRSaLKJWvAl4jvfVL43rndLfTw+n9vLvd/2F1odwJvgy+Cr4JesF+0A9+DE6Cl0Ec/BG8D/4M/tr4e5Nsfr357dL19q0V5n5Qa5u7/wBGwJ7r</latexit><latexit sha1_base64="MHw/TabkLT3RqXx2r462XmZzKDE=">AAAHeHicfVVdb9s2FFW7Lem0j6br417Yxca2wnbsFFmaFQGMpShWoMGy2U0LmF5GSVcWa5LSSKqxS+hX7df0dfsXe9ql7SyRk42AJOrynnt4Lw/JqBDc2G73/a3bH3z40cbmnY/DTz797PO7W/e+ODV5qWN4Geci168jZkBwBS8ttwJeFxqYjAS8iqZHfvzVW9CG52po5wWMJZsonvKYWTSdbR2f6BGiIbaEW5CkwRukQZ9QxFj6BPtHjTFpHBKaahY7+NWdnvGqctSU8sy9IZQrclQtzG+qqnG2td3tdBeNXO/0Vp3tYNVOzu5t3KdJHpcSlI0FM2bU6xZ27Ji2PBZQhbQ0ULB4yiYwwq5iEszYLfKuSBMtCUlzjY+yZGENr0IwjmbzWhRnWVQKpmd1a5TnUxwxVRjWOW36eOy4KkoLKl5SpqUgNie+nCThGmsn5qTOa/n0XUvxGHzZWkwayWzWKrifZ8tO37UnmhVZS7IpxCDEpWk5Kw8XPNJMz30K+blpRRh5ovNSJaZVMGtBK4N4q/msZTJWgGml3LZiJmL/n3hMIXIrmZ6a/4rakWAZDi4qJ8C6YZla+AWSymlIHjzuPogE8l71sBlMNICq3OLjfc4zlM6aTyRKqJx/X/EImySztjDf7+xYmHWMxdgwizOmJtCJc7nzewnG69Ls9L7bO9g92DEgOUoxQrXK9jm3Wdsn0eaqHaHIQS/8Hu1vLz8h9QVluAl8fUI6EXnEBMVf6mF9UKbU0E9ygQLo4xaI8wQOqQbBZhfYHCdfF9Fo2Bs7v3BeALVVPhkOmPLF1aDgHBOQTCWOpkxyMU8gZaWwfq+kF/26SEzqVVGFzatkBlcQksNu56AVS46kKAuBkkcCOzOpD1FPEmNTZWc+VH8JdubhCPfa3rhaT+op4CbTMJjLKBfPMCW3jGIq99Pxi8opTyF55WTlOE6XDsDe5IyGZB0SrSArDg8YlBEupy39kt5MsM4weHbsS3JBMOzVyueiWeWMuCTxzku0e46evgZMFBmrLqf62/O1qicTATzO2sva3zSCC23weKmfD9KHubrKcsAnEpnoUlU+nKORdHRpr67JQr7AYzm5CbEaqOoUD+ksYnqE4qNZlM8cfevfzZBmuhRAMuCTzOLpur9XWNIkwwwIi23JBEFYSKd4QnQ7u3swa5KL1iRP8UphKgYSgT3H/et9CZIRsyhjuKRqhoQsArS7nR7I5gV6kOUaq8PVhOSKoKiIgNQSwxPwiCt5bfeqf4PgBfDof4PoRSaLKJWvAl4jvfVL43rndLfTw+n9vLvd/2F1odwJvgy+Cr4JesF+0A9+DE6Cl0Ec/BG8D/4M/tr4e5Nsfr357dL19q0V5n5Qa5u7/wBGwJ7r</latexit><latexit sha1_base64="MHw/TabkLT3RqXx2r462XmZzKDE=">AAAHeHicfVVdb9s2FFW7Lem0j6br417Yxca2wnbsFFmaFQGMpShWoMGy2U0LmF5GSVcWa5LSSKqxS+hX7df0dfsXe9ql7SyRk42AJOrynnt4Lw/JqBDc2G73/a3bH3z40cbmnY/DTz797PO7W/e+ODV5qWN4Geci168jZkBwBS8ttwJeFxqYjAS8iqZHfvzVW9CG52po5wWMJZsonvKYWTSdbR2f6BGiIbaEW5CkwRukQZ9QxFj6BPtHjTFpHBKaahY7+NWdnvGqctSU8sy9IZQrclQtzG+qqnG2td3tdBeNXO/0Vp3tYNVOzu5t3KdJHpcSlI0FM2bU6xZ27Ji2PBZQhbQ0ULB4yiYwwq5iEszYLfKuSBMtCUlzjY+yZGENr0IwjmbzWhRnWVQKpmd1a5TnUxwxVRjWOW36eOy4KkoLKl5SpqUgNie+nCThGmsn5qTOa/n0XUvxGHzZWkwayWzWKrifZ8tO37UnmhVZS7IpxCDEpWk5Kw8XPNJMz30K+blpRRh5ovNSJaZVMGtBK4N4q/msZTJWgGml3LZiJmL/n3hMIXIrmZ6a/4rakWAZDi4qJ8C6YZla+AWSymlIHjzuPogE8l71sBlMNICq3OLjfc4zlM6aTyRKqJx/X/EImySztjDf7+xYmHWMxdgwizOmJtCJc7nzewnG69Ls9L7bO9g92DEgOUoxQrXK9jm3Wdsn0eaqHaHIQS/8Hu1vLz8h9QVluAl8fUI6EXnEBMVf6mF9UKbU0E9ygQLo4xaI8wQOqQbBZhfYHCdfF9Fo2Bs7v3BeALVVPhkOmPLF1aDgHBOQTCWOpkxyMU8gZaWwfq+kF/26SEzqVVGFzatkBlcQksNu56AVS46kKAuBkkcCOzOpD1FPEmNTZWc+VH8JdubhCPfa3rhaT+op4CbTMJjLKBfPMCW3jGIq99Pxi8opTyF55WTlOE6XDsDe5IyGZB0SrSArDg8YlBEupy39kt5MsM4weHbsS3JBMOzVyueiWeWMuCTxzku0e46evgZMFBmrLqf62/O1qicTATzO2sva3zSCC23weKmfD9KHubrKcsAnEpnoUlU+nKORdHRpr67JQr7AYzm5CbEaqOoUD+ksYnqE4qNZlM8cfevfzZBmuhRAMuCTzOLpur9XWNIkwwwIi23JBEFYSKd4QnQ7u3swa5KL1iRP8UphKgYSgT3H/et9CZIRsyhjuKRqhoQsArS7nR7I5gV6kOUaq8PVhOSKoKiIgNQSwxPwiCt5bfeqf4PgBfDof4PoRSaLKJWvAl4jvfVL43rndLfTw+n9vLvd/2F1odwJvgy+Cr4JesF+0A9+DE6Cl0Ec/BG8D/4M/tr4e5Nsfr357dL19q0V5n5Qa5u7/wBGwJ7r</latexit><latexit sha1_base64="MHw/TabkLT3RqXx2r462XmZzKDE=">AAAHeHicfVVdb9s2FFW7Lem0j6br417Yxca2wnbsFFmaFQGMpShWoMGy2U0LmF5GSVcWa5LSSKqxS+hX7df0dfsXe9ql7SyRk42AJOrynnt4Lw/JqBDc2G73/a3bH3z40cbmnY/DTz797PO7W/e+ODV5qWN4Geci168jZkBwBS8ttwJeFxqYjAS8iqZHfvzVW9CG52po5wWMJZsonvKYWTSdbR2f6BGiIbaEW5CkwRukQZ9QxFj6BPtHjTFpHBKaahY7+NWdnvGqctSU8sy9IZQrclQtzG+qqnG2td3tdBeNXO/0Vp3tYNVOzu5t3KdJHpcSlI0FM2bU6xZ27Ji2PBZQhbQ0ULB4yiYwwq5iEszYLfKuSBMtCUlzjY+yZGENr0IwjmbzWhRnWVQKpmd1a5TnUxwxVRjWOW36eOy4KkoLKl5SpqUgNie+nCThGmsn5qTOa/n0XUvxGHzZWkwayWzWKrifZ8tO37UnmhVZS7IpxCDEpWk5Kw8XPNJMz30K+blpRRh5ovNSJaZVMGtBK4N4q/msZTJWgGml3LZiJmL/n3hMIXIrmZ6a/4rakWAZDi4qJ8C6YZla+AWSymlIHjzuPogE8l71sBlMNICq3OLjfc4zlM6aTyRKqJx/X/EImySztjDf7+xYmHWMxdgwizOmJtCJc7nzewnG69Ls9L7bO9g92DEgOUoxQrXK9jm3Wdsn0eaqHaHIQS/8Hu1vLz8h9QVluAl8fUI6EXnEBMVf6mF9UKbU0E9ygQLo4xaI8wQOqQbBZhfYHCdfF9Fo2Bs7v3BeALVVPhkOmPLF1aDgHBOQTCWOpkxyMU8gZaWwfq+kF/26SEzqVVGFzatkBlcQksNu56AVS46kKAuBkkcCOzOpD1FPEmNTZWc+VH8JdubhCPfa3rhaT+op4CbTMJjLKBfPMCW3jGIq99Pxi8opTyF55WTlOE6XDsDe5IyGZB0SrSArDg8YlBEupy39kt5MsM4weHbsS3JBMOzVyueiWeWMuCTxzku0e46evgZMFBmrLqf62/O1qicTATzO2sva3zSCC23weKmfD9KHubrKcsAnEpnoUlU+nKORdHRpr67JQr7AYzm5CbEaqOoUD+ksYnqE4qNZlM8cfevfzZBmuhRAMuCTzOLpur9XWNIkwwwIi23JBEFYSKd4QnQ7u3swa5KL1iRP8UphKgYSgT3H/et9CZIRsyhjuKRqhoQsArS7nR7I5gV6kOUaq8PVhOSKoKiIgNQSwxPwiCt5bfeqf4PgBfDof4PoRSaLKJWvAl4jvfVL43rndLfTw+n9vLvd/2F1odwJvgy+Cr4JesF+0A9+DE6Cl0Ec/BG8D/4M/tr4e5Nsfr357dL19q0V5n5Qa5u7/wBGwJ7r</latexit>
Vi = T
i x<latexit sha1_base64="WMg3r0ygm8YS1z2N1nlA4xcLFbY=">AAAHPXicfVXdbts2FFbbzeu0v7S93A271MBQyI6dIkszIICxFcUKtFg2O2mByM0o6UgiTFIqSTVyCb3Kbre32HPsAXY37Ha3O7SdxXKyEbBFkec73/n5REYlZ9oMBr/fuHnrvfc7H9z+0P/o408+/Wzrzt0TXVQqhuO44IV6FVENnEk4NsxweFUqoCLi8DKafev2X74FpVkhJ2ZewlTQTLKUxdTg0tnW3QcnZ4wckjACQ8/Y60n94Gxre9AfLAa5OhmuJtveahyd3encC5MirgRIE3Oq9elwUJqppcqwmEPjh5WGksYzmsEpTiUVoKd2EXxDuriSkLRQ+JOGLFb9dQj6UXTe8mINjSpOVd1ejYpihju68f02p0kfTy2TZWVAxkvKtOLEFMTVhCRMQWz4nLR5DZu9CySLIVU0DqjQgpo8KJmLMzCzd71M0TIPBJ1BDJxfLi2jcnDOIkXV3KVQnOsgQs+ZKiqZ6KCkxoCSGvFGsTrQOS1BBykzQUx57N4Thyl5YQRVM/1fXvsCW4ebi8pxMHZSpQZ+hKSxCpL7jwf3I4686xYmh0wByMYuHs7mPGcGNmwiXkFj3f+ahd8luTGl/npnx0Dd1wZ9Qx3nVGbQjwux86YC7cSld4Zf7R3sHuxoEAw1GKHkRO+cmbznkugx2YtQqaAWdo/2t5cPP3QFpahkVx8/zHgRUR7ia+hgI5C6UjBKCo4CGKGO4yKBw1ABp/UFtsDg2yI6nQyn1jXOCaDV5aPJmEpXXAUSzjEBQWViw5QKxucJpLTiprGhTi/mbZHo1Kmi8bvrZBo7CMnhoH8QxIIhKcqCo+SRwNQ6dS7aSaLvUJrauRotwVY/PMVvbW/abCb1BPAjUzCei6jgTzElu/SiG/v9i+eNlY5CsMaKxjIMNxyDuc4YF5JNSLSCrDgcYFxF2E5TuZZeT7DJMH76wpXkgmAybJXPRnVjNb8kccZLtH2Glq4GlJc5bS5D/enZRtWTjAOL896y9tftYKM1Hi/t80E4N+tdFmOWCWQKl6py7mwYCRsu15srshDP8WxNrkOsNpo2xcOwjqg6RfGFeVTUNnzr/rt+mKuKA8mBZbnB03V/rzSkSyY5EBqbinKCMD+c4Qkx6O/uQd0lF6NLnuC9QGUMBA/tc/x+nS1BMqIXZfSXVF2fkIWD3qA/BNG9QI/zQmF1mMxIIQmKinBIDdEsAYdYy2t72PzrBC+AR//rRC0yWXhpXBXwGhluXhpXJye7/SGG98Pu9uib1YVy2/vc+8L70ht6+97I+8478o692Ku9n71fvF87v3X+6PzZ+WtpevPGCnPPa43O3/8AAp+L5g==</latexit><latexit sha1_base64="WMg3r0ygm8YS1z2N1nlA4xcLFbY=">AAAHPXicfVXdbts2FFbbzeu0v7S93A271MBQyI6dIkszIICxFcUKtFg2O2mByM0o6UgiTFIqSTVyCb3Kbre32HPsAXY37Ha3O7SdxXKyEbBFkec73/n5REYlZ9oMBr/fuHnrvfc7H9z+0P/o408+/Wzrzt0TXVQqhuO44IV6FVENnEk4NsxweFUqoCLi8DKafev2X74FpVkhJ2ZewlTQTLKUxdTg0tnW3QcnZ4wckjACQ8/Y60n94Gxre9AfLAa5OhmuJtveahyd3encC5MirgRIE3Oq9elwUJqppcqwmEPjh5WGksYzmsEpTiUVoKd2EXxDuriSkLRQ+JOGLFb9dQj6UXTe8mINjSpOVd1ejYpihju68f02p0kfTy2TZWVAxkvKtOLEFMTVhCRMQWz4nLR5DZu9CySLIVU0DqjQgpo8KJmLMzCzd71M0TIPBJ1BDJxfLi2jcnDOIkXV3KVQnOsgQs+ZKiqZ6KCkxoCSGvFGsTrQOS1BBykzQUx57N4Thyl5YQRVM/1fXvsCW4ebi8pxMHZSpQZ+hKSxCpL7jwf3I4686xYmh0wByMYuHs7mPGcGNmwiXkFj3f+ahd8luTGl/npnx0Dd1wZ9Qx3nVGbQjwux86YC7cSld4Zf7R3sHuxoEAw1GKHkRO+cmbznkugx2YtQqaAWdo/2t5cPP3QFpahkVx8/zHgRUR7ia+hgI5C6UjBKCo4CGKGO4yKBw1ABp/UFtsDg2yI6nQyn1jXOCaDV5aPJmEpXXAUSzjEBQWViw5QKxucJpLTiprGhTi/mbZHo1Kmi8bvrZBo7CMnhoH8QxIIhKcqCo+SRwNQ6dS7aSaLvUJrauRotwVY/PMVvbW/abCb1BPAjUzCei6jgTzElu/SiG/v9i+eNlY5CsMaKxjIMNxyDuc4YF5JNSLSCrDgcYFxF2E5TuZZeT7DJMH76wpXkgmAybJXPRnVjNb8kccZLtH2Glq4GlJc5bS5D/enZRtWTjAOL896y9tftYKM1Hi/t80E4N+tdFmOWCWQKl6py7mwYCRsu15srshDP8WxNrkOsNpo2xcOwjqg6RfGFeVTUNnzr/rt+mKuKA8mBZbnB03V/rzSkSyY5EBqbinKCMD+c4Qkx6O/uQd0lF6NLnuC9QGUMBA/tc/x+nS1BMqIXZfSXVF2fkIWD3qA/BNG9QI/zQmF1mMxIIQmKinBIDdEsAYdYy2t72PzrBC+AR//rRC0yWXhpXBXwGhluXhpXJye7/SGG98Pu9uib1YVy2/vc+8L70ht6+97I+8478o692Ku9n71fvF87v3X+6PzZ+WtpevPGCnPPa43O3/8AAp+L5g==</latexit><latexit sha1_base64="WMg3r0ygm8YS1z2N1nlA4xcLFbY=">AAAHPXicfVXdbts2FFbbzeu0v7S93A271MBQyI6dIkszIICxFcUKtFg2O2mByM0o6UgiTFIqSTVyCb3Kbre32HPsAXY37Ha3O7SdxXKyEbBFkec73/n5REYlZ9oMBr/fuHnrvfc7H9z+0P/o408+/Wzrzt0TXVQqhuO44IV6FVENnEk4NsxweFUqoCLi8DKafev2X74FpVkhJ2ZewlTQTLKUxdTg0tnW3QcnZ4wckjACQ8/Y60n94Gxre9AfLAa5OhmuJtveahyd3encC5MirgRIE3Oq9elwUJqppcqwmEPjh5WGksYzmsEpTiUVoKd2EXxDuriSkLRQ+JOGLFb9dQj6UXTe8mINjSpOVd1ejYpihju68f02p0kfTy2TZWVAxkvKtOLEFMTVhCRMQWz4nLR5DZu9CySLIVU0DqjQgpo8KJmLMzCzd71M0TIPBJ1BDJxfLi2jcnDOIkXV3KVQnOsgQs+ZKiqZ6KCkxoCSGvFGsTrQOS1BBykzQUx57N4Thyl5YQRVM/1fXvsCW4ebi8pxMHZSpQZ+hKSxCpL7jwf3I4686xYmh0wByMYuHs7mPGcGNmwiXkFj3f+ahd8luTGl/npnx0Dd1wZ9Qx3nVGbQjwux86YC7cSld4Zf7R3sHuxoEAw1GKHkRO+cmbznkugx2YtQqaAWdo/2t5cPP3QFpahkVx8/zHgRUR7ia+hgI5C6UjBKCo4CGKGO4yKBw1ABp/UFtsDg2yI6nQyn1jXOCaDV5aPJmEpXXAUSzjEBQWViw5QKxucJpLTiprGhTi/mbZHo1Kmi8bvrZBo7CMnhoH8QxIIhKcqCo+SRwNQ6dS7aSaLvUJrauRotwVY/PMVvbW/abCb1BPAjUzCei6jgTzElu/SiG/v9i+eNlY5CsMaKxjIMNxyDuc4YF5JNSLSCrDgcYFxF2E5TuZZeT7DJMH76wpXkgmAybJXPRnVjNb8kccZLtH2Glq4GlJc5bS5D/enZRtWTjAOL896y9tftYKM1Hi/t80E4N+tdFmOWCWQKl6py7mwYCRsu15srshDP8WxNrkOsNpo2xcOwjqg6RfGFeVTUNnzr/rt+mKuKA8mBZbnB03V/rzSkSyY5EBqbinKCMD+c4Qkx6O/uQd0lF6NLnuC9QGUMBA/tc/x+nS1BMqIXZfSXVF2fkIWD3qA/BNG9QI/zQmF1mMxIIQmKinBIDdEsAYdYy2t72PzrBC+AR//rRC0yWXhpXBXwGhluXhpXJye7/SGG98Pu9uib1YVy2/vc+8L70ht6+97I+8478o692Ku9n71fvF87v3X+6PzZ+WtpevPGCnPPa43O3/8AAp+L5g==</latexit><latexit sha1_base64="WMg3r0ygm8YS1z2N1nlA4xcLFbY=">AAAHPXicfVXdbts2FFbbzeu0v7S93A271MBQyI6dIkszIICxFcUKtFg2O2mByM0o6UgiTFIqSTVyCb3Kbre32HPsAXY37Ha3O7SdxXKyEbBFkec73/n5REYlZ9oMBr/fuHnrvfc7H9z+0P/o408+/Wzrzt0TXVQqhuO44IV6FVENnEk4NsxweFUqoCLi8DKafev2X74FpVkhJ2ZewlTQTLKUxdTg0tnW3QcnZ4wckjACQ8/Y60n94Gxre9AfLAa5OhmuJtveahyd3encC5MirgRIE3Oq9elwUJqppcqwmEPjh5WGksYzmsEpTiUVoKd2EXxDuriSkLRQ+JOGLFb9dQj6UXTe8mINjSpOVd1ejYpihju68f02p0kfTy2TZWVAxkvKtOLEFMTVhCRMQWz4nLR5DZu9CySLIVU0DqjQgpo8KJmLMzCzd71M0TIPBJ1BDJxfLi2jcnDOIkXV3KVQnOsgQs+ZKiqZ6KCkxoCSGvFGsTrQOS1BBykzQUx57N4Thyl5YQRVM/1fXvsCW4ebi8pxMHZSpQZ+hKSxCpL7jwf3I4686xYmh0wByMYuHs7mPGcGNmwiXkFj3f+ahd8luTGl/npnx0Dd1wZ9Qx3nVGbQjwux86YC7cSld4Zf7R3sHuxoEAw1GKHkRO+cmbznkugx2YtQqaAWdo/2t5cPP3QFpahkVx8/zHgRUR7ia+hgI5C6UjBKCo4CGKGO4yKBw1ABp/UFtsDg2yI6nQyn1jXOCaDV5aPJmEpXXAUSzjEBQWViw5QKxucJpLTiprGhTi/mbZHo1Kmi8bvrZBo7CMnhoH8QxIIhKcqCo+SRwNQ6dS7aSaLvUJrauRotwVY/PMVvbW/abCb1BPAjUzCei6jgTzElu/SiG/v9i+eNlY5CsMaKxjIMNxyDuc4YF5JNSLSCrDgcYFxF2E5TuZZeT7DJMH76wpXkgmAybJXPRnVjNb8kccZLtH2Glq4GlJc5bS5D/enZRtWTjAOL896y9tftYKM1Hi/t80E4N+tdFmOWCWQKl6py7mwYCRsu15srshDP8WxNrkOsNpo2xcOwjqg6RfGFeVTUNnzr/rt+mKuKA8mBZbnB03V/rzSkSyY5EBqbinKCMD+c4Qkx6O/uQd0lF6NLnuC9QGUMBA/tc/x+nS1BMqIXZfSXVF2fkIWD3qA/BNG9QI/zQmF1mMxIIQmKinBIDdEsAYdYy2t72PzrBC+AR//rRC0yWXhpXBXwGhluXhpXJye7/SGG98Pu9uib1YVy2/vc+8L70ht6+97I+8478o692Ku9n71fvF87v3X+6PzZ+WtpevPGCnPPa43O3/8AAp+L5g==</latexit>

26. A basic subset choice choice model could assume set
utility is additive in the elements.
26
• Observe choice set C with items 1, …, c. Choose two elements.
(repeats allowed)
• Random utility of (i, j) pair: Uij = Vi + Vj + eij
Vi is base utility, eij i.i.d. Gumbel distributed error
• If choosing the set with largest random utility…
Pr[select set {i, j} | C] = e
Vi+Vj
P
{k,l}⇢C eVk+Vl
<latexit sha1_base64="k8hNq795y+cv+adMlMxth/n2hx8=">AAAHlXicfVVdb9s2FFW6rem0r3R92MNe2CUGhk527BRZmhUBgiUIVqBFszlJC4ReRklXFmNS0kiqsUvwP+51f2Sv26XtLJaTTYAtirznHN7DSzKuBNem2/1z5d4HH350f/XBx+Enn372+RdrD78802WtEjhNSlGqtzHTIHgBp4YbAW8rBUzGAt7EowM//uYdKM3L4sRMKhhINix4xhNmsOti7fJYnSMaEkM0GLJBLY8uqdvA1nOKQEOfY/tgY0A29gjNFEss/GrPLjj5jpxdXDpnqa7lhaV2FBFBHcHP2DMduGncaBonnNsIL9bWu53u9CG3G715Yz2YP8cXD+8/ommZ1BIKkwim9XmvW5mBZcrwRIALaa2hYsmIDeEcmwWToAd2aoojLexJSVYq/BWGTHvDRQjyKDZpsFjD4lowNW72xmU5whHtwrCpabJnA8uLqjZQJDPJrBbElMR7TVKu0FgxIU1dw0fvo4In4O2MmNSSmTyquJ9nZEbv20PFqjySbAQJCHHTNZuVhwseK6YmPoXySkcxMg9VWRepjipmDKhCI94oPo50zirQUcZNlDCR+O/UYypRGsnUSP8Xa0eCYTg4dU6AsSd1ZuAXSJ1VkD5+1n0cC9RdjDA5DBVA4ez05WOucm5gKSYWNTjr/xciwhbJjan0D5ubBsYdbZAbxknOiiF0klJu/l6D9kWrN3vfb+9u7W5qkBxLNMZSlu0rbvK2T6LNi3aMOwDUNO7pzvrsFVJvKMMd4v0J6VCUMRMUP6mH7UOhawX7aSmwAPZxfyRlCntUgWDja2yJk28W0flJb2D9wvkCaKzy8UmfFd5cBQVcYQKSFamlGZNcTFLIWC2M3z3ZdbtZJDrzVeHC1qKYxhWEdK/b2Y0SyVEUy0JgyaOAGevMUzSTRG5amLGn2p+BrX5yjntte+CWkzoE3GQK+hMZl+IIU7IzFu3s61cvnS28hOTOSmc5Tpf2wdwVjB3pMiSeQ+YaHtDHcwIPrNov6d0Cywr9o1fekmuBk17DPhuPndXiRsQHz9D2BUZ6D5iocuZupvrbiyXX06EAnuTtmfd3jeBCazxemueD9DSLqyz7fChRic6qytNZGktLZ/3uVlnIl3hmp3ch5gOuKfGEjmOmzrH4aB6XY0vf+f9WSHNVCyA58GFu8HTd2a4MaZGTHAhLTM0EQVhIR3hCdDtb2zBukeunRQ7xvmFFAiQGc4X718cSFCN6amM4k2qFhEwJ2t1OD2TrGt3PS4Xu8GJIyoJgUREBGV4rPAWPWMhrvef+JcEL4On/kqhpJlMW513Aa6S3fGncbpxtdXo4vZ+31vd/nF8oD4Kvg2+Cb4NesBPsBz8Fx8FpkAR/BH8Ff68Eq1+t7q0erh7NQu+tzDGPgsaz+vofdD+nOw==</latexit><latexit sha1_base64="k8hNq795y+cv+adMlMxth/n2hx8=">AAAHlXicfVVdb9s2FFW6rem0r3R92MNe2CUGhk527BRZmhUBgiUIVqBFszlJC4ReRklXFmNS0kiqsUvwP+51f2Sv26XtLJaTTYAtirznHN7DSzKuBNem2/1z5d4HH350f/XBx+Enn372+RdrD78802WtEjhNSlGqtzHTIHgBp4YbAW8rBUzGAt7EowM//uYdKM3L4sRMKhhINix4xhNmsOti7fJYnSMaEkM0GLJBLY8uqdvA1nOKQEOfY/tgY0A29gjNFEss/GrPLjj5jpxdXDpnqa7lhaV2FBFBHcHP2DMduGncaBonnNsIL9bWu53u9CG3G715Yz2YP8cXD+8/ommZ1BIKkwim9XmvW5mBZcrwRIALaa2hYsmIDeEcmwWToAd2aoojLexJSVYq/BWGTHvDRQjyKDZpsFjD4lowNW72xmU5whHtwrCpabJnA8uLqjZQJDPJrBbElMR7TVKu0FgxIU1dw0fvo4In4O2MmNSSmTyquJ9nZEbv20PFqjySbAQJCHHTNZuVhwseK6YmPoXySkcxMg9VWRepjipmDKhCI94oPo50zirQUcZNlDCR+O/UYypRGsnUSP8Xa0eCYTg4dU6AsSd1ZuAXSJ1VkD5+1n0cC9RdjDA5DBVA4ez05WOucm5gKSYWNTjr/xciwhbJjan0D5ubBsYdbZAbxknOiiF0klJu/l6D9kWrN3vfb+9u7W5qkBxLNMZSlu0rbvK2T6LNi3aMOwDUNO7pzvrsFVJvKMMd4v0J6VCUMRMUP6mH7UOhawX7aSmwAPZxfyRlCntUgWDja2yJk28W0flJb2D9wvkCaKzy8UmfFd5cBQVcYQKSFamlGZNcTFLIWC2M3z3ZdbtZJDrzVeHC1qKYxhWEdK/b2Y0SyVEUy0JgyaOAGevMUzSTRG5amLGn2p+BrX5yjntte+CWkzoE3GQK+hMZl+IIU7IzFu3s61cvnS28hOTOSmc5Tpf2wdwVjB3pMiSeQ+YaHtDHcwIPrNov6d0Cywr9o1fekmuBk17DPhuPndXiRsQHz9D2BUZ6D5iocuZupvrbiyXX06EAnuTtmfd3jeBCazxemueD9DSLqyz7fChRic6qytNZGktLZ/3uVlnIl3hmp3ch5gOuKfGEjmOmzrH4aB6XY0vf+f9WSHNVCyA58GFu8HTd2a4MaZGTHAhLTM0EQVhIR3hCdDtb2zBukeunRQ7xvmFFAiQGc4X718cSFCN6amM4k2qFhEwJ2t1OD2TrGt3PS4Xu8GJIyoJgUREBGV4rPAWPWMhrvef+JcEL4On/kqhpJlMW513Aa6S3fGncbpxtdXo4vZ+31vd/nF8oD4Kvg2+Cb4NesBPsBz8Fx8FpkAR/BH8Ff68Eq1+t7q0erh7NQu+tzDGPgsaz+vofdD+nOw==</latexit><latexit sha1_base64="k8hNq795y+cv+adMlMxth/n2hx8=">AAAHlXicfVVdb9s2FFW6rem0r3R92MNe2CUGhk527BRZmhUBgiUIVqBFszlJC4ReRklXFmNS0kiqsUvwP+51f2Sv26XtLJaTTYAtirznHN7DSzKuBNem2/1z5d4HH350f/XBx+Enn372+RdrD78802WtEjhNSlGqtzHTIHgBp4YbAW8rBUzGAt7EowM//uYdKM3L4sRMKhhINix4xhNmsOti7fJYnSMaEkM0GLJBLY8uqdvA1nOKQEOfY/tgY0A29gjNFEss/GrPLjj5jpxdXDpnqa7lhaV2FBFBHcHP2DMduGncaBonnNsIL9bWu53u9CG3G715Yz2YP8cXD+8/ommZ1BIKkwim9XmvW5mBZcrwRIALaa2hYsmIDeEcmwWToAd2aoojLexJSVYq/BWGTHvDRQjyKDZpsFjD4lowNW72xmU5whHtwrCpabJnA8uLqjZQJDPJrBbElMR7TVKu0FgxIU1dw0fvo4In4O2MmNSSmTyquJ9nZEbv20PFqjySbAQJCHHTNZuVhwseK6YmPoXySkcxMg9VWRepjipmDKhCI94oPo50zirQUcZNlDCR+O/UYypRGsnUSP8Xa0eCYTg4dU6AsSd1ZuAXSJ1VkD5+1n0cC9RdjDA5DBVA4ez05WOucm5gKSYWNTjr/xciwhbJjan0D5ubBsYdbZAbxknOiiF0klJu/l6D9kWrN3vfb+9u7W5qkBxLNMZSlu0rbvK2T6LNi3aMOwDUNO7pzvrsFVJvKMMd4v0J6VCUMRMUP6mH7UOhawX7aSmwAPZxfyRlCntUgWDja2yJk28W0flJb2D9wvkCaKzy8UmfFd5cBQVcYQKSFamlGZNcTFLIWC2M3z3ZdbtZJDrzVeHC1qKYxhWEdK/b2Y0SyVEUy0JgyaOAGevMUzSTRG5amLGn2p+BrX5yjntte+CWkzoE3GQK+hMZl+IIU7IzFu3s61cvnS28hOTOSmc5Tpf2wdwVjB3pMiSeQ+YaHtDHcwIPrNov6d0Cywr9o1fekmuBk17DPhuPndXiRsQHz9D2BUZ6D5iocuZupvrbiyXX06EAnuTtmfd3jeBCazxemueD9DSLqyz7fChRic6qytNZGktLZ/3uVlnIl3hmp3ch5gOuKfGEjmOmzrH4aB6XY0vf+f9WSHNVCyA58GFu8HTd2a4MaZGTHAhLTM0EQVhIR3hCdDtb2zBukeunRQ7xvmFFAiQGc4X718cSFCN6amM4k2qFhEwJ2t1OD2TrGt3PS4Xu8GJIyoJgUREBGV4rPAWPWMhrvef+JcEL4On/kqhpJlMW513Aa6S3fGncbpxtdXo4vZ+31vd/nF8oD4Kvg2+Cb4NesBPsBz8Fx8FpkAR/BH8Ff68Eq1+t7q0erh7NQu+tzDGPgsaz+vofdD+nOw==</latexit><latexit sha1_base64="k8hNq795y+cv+adMlMxth/n2hx8=">AAAHlXicfVVdb9s2FFW6rem0r3R92MNe2CUGhk527BRZmhUBgiUIVqBFszlJC4ReRklXFmNS0kiqsUvwP+51f2Sv26XtLJaTTYAtirznHN7DSzKuBNem2/1z5d4HH350f/XBx+Enn372+RdrD78802WtEjhNSlGqtzHTIHgBp4YbAW8rBUzGAt7EowM//uYdKM3L4sRMKhhINix4xhNmsOti7fJYnSMaEkM0GLJBLY8uqdvA1nOKQEOfY/tgY0A29gjNFEss/GrPLjj5jpxdXDpnqa7lhaV2FBFBHcHP2DMduGncaBonnNsIL9bWu53u9CG3G715Yz2YP8cXD+8/ommZ1BIKkwim9XmvW5mBZcrwRIALaa2hYsmIDeEcmwWToAd2aoojLexJSVYq/BWGTHvDRQjyKDZpsFjD4lowNW72xmU5whHtwrCpabJnA8uLqjZQJDPJrBbElMR7TVKu0FgxIU1dw0fvo4In4O2MmNSSmTyquJ9nZEbv20PFqjySbAQJCHHTNZuVhwseK6YmPoXySkcxMg9VWRepjipmDKhCI94oPo50zirQUcZNlDCR+O/UYypRGsnUSP8Xa0eCYTg4dU6AsSd1ZuAXSJ1VkD5+1n0cC9RdjDA5DBVA4ez05WOucm5gKSYWNTjr/xciwhbJjan0D5ubBsYdbZAbxknOiiF0klJu/l6D9kWrN3vfb+9u7W5qkBxLNMZSlu0rbvK2T6LNi3aMOwDUNO7pzvrsFVJvKMMd4v0J6VCUMRMUP6mH7UOhawX7aSmwAPZxfyRlCntUgWDja2yJk28W0flJb2D9wvkCaKzy8UmfFd5cBQVcYQKSFamlGZNcTFLIWC2M3z3ZdbtZJDrzVeHC1qKYxhWEdK/b2Y0SyVEUy0JgyaOAGevMUzSTRG5amLGn2p+BrX5yjntte+CWkzoE3GQK+hMZl+IIU7IzFu3s61cvnS28hOTOSmc5Tpf2wdwVjB3pMiSeQ+YaHtDHcwIPrNov6d0Cywr9o1fekmuBk17DPhuPndXiRsQHz9D2BUZ6D5iocuZupvrbiyXX06EAnuTtmfd3jeBCazxemueD9DSLqyz7fChRic6qytNZGktLZ/3uVlnIl3hmp3ch5gOuKfGEjmOmzrH4aB6XY0vf+f9WSHNVCyA58GFu8HTd2a4MaZGTHAhLTM0EQVhIR3hCdDtb2zBukeunRQ7xvmFFAiQGc4X718cSFCN6amM4k2qFhEwJ2t1OD2TrGt3PS4Xu8GJIyoJgUREBGV4rPAWPWMhrvef+JcEL4On/kqhpJlMW513Aa6S3fGncbpxtdXo4vZ+31vd/nF8oD4Kvg2+Cb4NesBPsBz8Fx8FpkAR/BH8Ff68Eq1+t7q0erh7NQu+tzDGPgsaz+vofdD+nOw==</latexit>
Pr[select set {i, j} | C, j] = eVi
P
k2C eVk
<latexit sha1_base64="ZaJhcD7ScvxQtNfQTogu245TRXE=">AAAHg3icfVVdb9s2FFW7te60j6br417YxQaGTnbsdFmaFQEMpChaoMWy2UkDmF5GSVcWa1LSSKqxS+iv7X/sfa/bb9il7SyWk42AJOrynnt4Dy/JsBBcm273j1u3P/r4zt3GvU/8Tz/7/Iv7Ww++PNV5qSI4iXKRq7OQaRA8gxPDjYCzQgGToYC34fTIjb99D0rzPBuaeQFjySYZT3jEDJrOt86O1QjREBmiwZAmtTx4R6sm9p5RBBr6DPtHzYA03zXHpHlIaKJYZOEXe3rOq8pSXcpzOyWUZ+SoWpinVdX0z7e2u53uopHrnd6qs+2t2vH5g7sPaZxHpYTMRIJpPep1CzO2TBkeCah8WmooWDRlExhhN2MS9NguJKhICy0xSXKFT2bIwuqvQzCOYvNaFGtYWAqmZnVrmOdTHNGV79c5TfJ0bHlWlAayaEmZlIKYnDhlScwVyijmpM5r+PRDkPEInG4Bk1oykwYFd/MMzPRDe6JYkQaSTSECIa5My1k5uOChYmruUsgvdBBi5InKyyzWQcGMAZVpxBvFZ4FOWQE6SLgJIiYi9x87TCFyI5ma6v+K2pFgGA4ulBNg7LBMDPwMcWUVxI+edh+FAnnXPUwKEwWQVXbxcT4XKTew4ROKEirr3msefoukxhT6h50dA7OONhgbZlHKsgl0olzu/FaCdiWqd3rf7x3sHuxokBwLMsTCle0LbtK2S6LNs3aI9Q5q4fdkf3v58akTlOF+cPr4dCLykAmKv9TB+pDpUkE/zgUWQB93Q5THcEgVCDa7xOY4+XoRjYa9sXUL5wqgtsrHwwHLnLgKMrjABCTLYksTJrmYx5CwUhi3WZLLfr1IdOKqovJb62QaVxDiw27nIIgkR1IsC4EljwRmphMXop4kxqaZmblQ/SXY6scj3Gt742ozqeeAm0zBYC7DXLzAlOwyiq7sj29eVzZzFJJXVlaW43TpAMxNzmiINyHhCrLicIBBGeJymtIt6c0EmwyDF2+cJJcEw15NPhvOKqvFFYlzXqLtK/R0GjBRpKy6muqvrzZUjycCeJS2l9rfNIILrfF4qZ8P0oVZX2U54BOJTHRZVS6cpaG0dGmvrpWFfI0ndHwTYjVQ1Ske01nI1AiLj6ZhPrP0vXu3fJqqUgBJgU9Sg6fr/l5hSIsMUyAsMiUTBGE+neIJ0e3s7sGsRS5bizzH24VlEZAQzAXuX+dLkIzohYz+kqrlE7II0O52eiBbl+hBmitUh2cTkmcEi4oISPAS4TE4xFpe273q3yB4ATz53yBqkckiSuVUwGukt3lpXO+c7nZ6OL2fdrf7L1cXyj3vK+9r7xuv5+17fe+ld+ydeJH3u/en95f3d+NO49vGbuO7pevtWyvMQ6/WGof/AOdZoU0=</latexit><latexit sha1_base64="ZaJhcD7ScvxQtNfQTogu245TRXE=">AAAHg3icfVVdb9s2FFW7te60j6br417YxQaGTnbsdFmaFQEMpChaoMWy2UkDmF5GSVcWa1LSSKqxS+iv7X/sfa/bb9il7SyWk42AJOrynnt4Dy/JsBBcm273j1u3P/r4zt3GvU/8Tz/7/Iv7Ww++PNV5qSI4iXKRq7OQaRA8gxPDjYCzQgGToYC34fTIjb99D0rzPBuaeQFjySYZT3jEDJrOt86O1QjREBmiwZAmtTx4R6sm9p5RBBr6DPtHzYA03zXHpHlIaKJYZOEXe3rOq8pSXcpzOyWUZ+SoWpinVdX0z7e2u53uopHrnd6qs+2t2vH5g7sPaZxHpYTMRIJpPep1CzO2TBkeCah8WmooWDRlExhhN2MS9NguJKhICy0xSXKFT2bIwuqvQzCOYvNaFGtYWAqmZnVrmOdTHNGV79c5TfJ0bHlWlAayaEmZlIKYnDhlScwVyijmpM5r+PRDkPEInG4Bk1oykwYFd/MMzPRDe6JYkQaSTSECIa5My1k5uOChYmruUsgvdBBi5InKyyzWQcGMAZVpxBvFZ4FOWQE6SLgJIiYi9x87TCFyI5ma6v+K2pFgGA4ulBNg7LBMDPwMcWUVxI+edh+FAnnXPUwKEwWQVXbxcT4XKTew4ROKEirr3msefoukxhT6h50dA7OONhgbZlHKsgl0olzu/FaCdiWqd3rf7x3sHuxokBwLMsTCle0LbtK2S6LNs3aI9Q5q4fdkf3v58akTlOF+cPr4dCLykAmKv9TB+pDpUkE/zgUWQB93Q5THcEgVCDa7xOY4+XoRjYa9sXUL5wqgtsrHwwHLnLgKMrjABCTLYksTJrmYx5CwUhi3WZLLfr1IdOKqovJb62QaVxDiw27nIIgkR1IsC4EljwRmphMXop4kxqaZmblQ/SXY6scj3Gt742ozqeeAm0zBYC7DXLzAlOwyiq7sj29eVzZzFJJXVlaW43TpAMxNzmiINyHhCrLicIBBGeJymtIt6c0EmwyDF2+cJJcEw15NPhvOKqvFFYlzXqLtK/R0GjBRpKy6muqvrzZUjycCeJS2l9rfNIILrfF4qZ8P0oVZX2U54BOJTHRZVS6cpaG0dGmvrpWFfI0ndHwTYjVQ1Ske01nI1AiLj6ZhPrP0vXu3fJqqUgBJgU9Sg6fr/l5hSIsMUyAsMiUTBGE+neIJ0e3s7sGsRS5bizzH24VlEZAQzAXuX+dLkIzohYz+kqrlE7II0O52eiBbl+hBmitUh2cTkmcEi4oISPAS4TE4xFpe273q3yB4ATz53yBqkckiSuVUwGukt3lpXO+c7nZ6OL2fdrf7L1cXyj3vK+9r7xuv5+17fe+ld+ydeJH3u/en95f3d+NO49vGbuO7pevtWyvMQ6/WGof/AOdZoU0=</latexit><latexit sha1_base64="ZaJhcD7ScvxQtNfQTogu245TRXE=">AAAHg3icfVVdb9s2FFW7te60j6br417YxQaGTnbsdFmaFQEMpChaoMWy2UkDmF5GSVcWa1LSSKqxS+iv7X/sfa/bb9il7SyWk42AJOrynnt4Dy/JsBBcm273j1u3P/r4zt3GvU/8Tz/7/Iv7Ww++PNV5qSI4iXKRq7OQaRA8gxPDjYCzQgGToYC34fTIjb99D0rzPBuaeQFjySYZT3jEDJrOt86O1QjREBmiwZAmtTx4R6sm9p5RBBr6DPtHzYA03zXHpHlIaKJYZOEXe3rOq8pSXcpzOyWUZ+SoWpinVdX0z7e2u53uopHrnd6qs+2t2vH5g7sPaZxHpYTMRIJpPep1CzO2TBkeCah8WmooWDRlExhhN2MS9NguJKhICy0xSXKFT2bIwuqvQzCOYvNaFGtYWAqmZnVrmOdTHNGV79c5TfJ0bHlWlAayaEmZlIKYnDhlScwVyijmpM5r+PRDkPEInG4Bk1oykwYFd/MMzPRDe6JYkQaSTSECIa5My1k5uOChYmruUsgvdBBi5InKyyzWQcGMAZVpxBvFZ4FOWQE6SLgJIiYi9x87TCFyI5ma6v+K2pFgGA4ulBNg7LBMDPwMcWUVxI+edh+FAnnXPUwKEwWQVXbxcT4XKTew4ROKEirr3msefoukxhT6h50dA7OONhgbZlHKsgl0olzu/FaCdiWqd3rf7x3sHuxokBwLMsTCle0LbtK2S6LNs3aI9Q5q4fdkf3v58akTlOF+cPr4dCLykAmKv9TB+pDpUkE/zgUWQB93Q5THcEgVCDa7xOY4+XoRjYa9sXUL5wqgtsrHwwHLnLgKMrjABCTLYksTJrmYx5CwUhi3WZLLfr1IdOKqovJb62QaVxDiw27nIIgkR1IsC4EljwRmphMXop4kxqaZmblQ/SXY6scj3Gt742ozqeeAm0zBYC7DXLzAlOwyiq7sj29eVzZzFJJXVlaW43TpAMxNzmiINyHhCrLicIBBGeJymtIt6c0EmwyDF2+cJJcEw15NPhvOKqvFFYlzXqLtK/R0GjBRpKy6muqvrzZUjycCeJS2l9rfNIILrfF4qZ8P0oVZX2U54BOJTHRZVS6cpaG0dGmvrpWFfI0ndHwTYjVQ1Ske01nI1AiLj6ZhPrP0vXu3fJqqUgBJgU9Sg6fr/l5hSIsMUyAsMiUTBGE+neIJ0e3s7sGsRS5bizzH24VlEZAQzAXuX+dLkIzohYz+kqrlE7II0O52eiBbl+hBmitUh2cTkmcEi4oISPAS4TE4xFpe273q3yB4ATz53yBqkckiSuVUwGukt3lpXO+c7nZ6OL2fdrf7L1cXyj3vK+9r7xuv5+17fe+ld+ydeJH3u/en95f3d+NO49vGbuO7pevtWyvMQ6/WGof/AOdZoU0=</latexit><latexit sha1_base64="ZaJhcD7ScvxQtNfQTogu245TRXE=">AAAHg3icfVVdb9s2FFW7te60j6br417YxQaGTnbsdFmaFQEMpChaoMWy2UkDmF5GSVcWa1LSSKqxS+iv7X/sfa/bb9il7SyWk42AJOrynnt4Dy/JsBBcm273j1u3P/r4zt3GvU/8Tz/7/Iv7Ww++PNV5qSI4iXKRq7OQaRA8gxPDjYCzQgGToYC34fTIjb99D0rzPBuaeQFjySYZT3jEDJrOt86O1QjREBmiwZAmtTx4R6sm9p5RBBr6DPtHzYA03zXHpHlIaKJYZOEXe3rOq8pSXcpzOyWUZ+SoWpinVdX0z7e2u53uopHrnd6qs+2t2vH5g7sPaZxHpYTMRIJpPep1CzO2TBkeCah8WmooWDRlExhhN2MS9NguJKhICy0xSXKFT2bIwuqvQzCOYvNaFGtYWAqmZnVrmOdTHNGV79c5TfJ0bHlWlAayaEmZlIKYnDhlScwVyijmpM5r+PRDkPEInG4Bk1oykwYFd/MMzPRDe6JYkQaSTSECIa5My1k5uOChYmruUsgvdBBi5InKyyzWQcGMAZVpxBvFZ4FOWQE6SLgJIiYi9x87TCFyI5ma6v+K2pFgGA4ulBNg7LBMDPwMcWUVxI+edh+FAnnXPUwKEwWQVXbxcT4XKTew4ROKEirr3msefoukxhT6h50dA7OONhgbZlHKsgl0olzu/FaCdiWqd3rf7x3sHuxokBwLMsTCle0LbtK2S6LNs3aI9Q5q4fdkf3v58akTlOF+cPr4dCLykAmKv9TB+pDpUkE/zgUWQB93Q5THcEgVCDa7xOY4+XoRjYa9sXUL5wqgtsrHwwHLnLgKMrjABCTLYksTJrmYx5CwUhi3WZLLfr1IdOKqovJb62QaVxDiw27nIIgkR1IsC4EljwRmphMXop4kxqaZmblQ/SXY6scj3Gt742ozqeeAm0zBYC7DXLzAlOwyiq7sj29eVzZzFJJXVlaW43TpAMxNzmiINyHhCrLicIBBGeJymtIt6c0EmwyDF2+cJJcEw15NPhvOKqvFFYlzXqLtK/R0GjBRpKy6muqvrzZUjycCeJS2l9rfNIILrfF4qZ8P0oVZX2U54BOJTHRZVS6cpaG0dGmvrpWFfI0ndHwTYjVQ1Ske01nI1AiLj6ZhPrP0vXu3fJqqUgBJgU9Sg6fr/l5hSIsMUyAsMiUTBGE+neIJ0e3s7sGsRS5bizzH24VlEZAQzAXuX+dLkIzohYz+kqrlE7II0O52eiBbl+hBmitUh2cTkmcEi4oISPAS4TE4xFpe273q3yB4ATz53yBqkckiSuVUwGukt3lpXO+c7nZ6OL2fdrf7L1cXyj3vK+9r7xuv5+17fe+ld+ydeJH3u/en95f3d+NO49vGbuO7pevtWyvMQ6/WGof/AOdZoU0=</latexit>
Observation. Probability of selecting i, given j, is the same for all j.

27. Our“sparse model”allows some pairs to have
additional corrective utility.
27
Corrective utility Small collection of “special sets”
Uij =
(
Vi + Vj + eij {i, j} /2 H
Vi + Vj + Wij + eij {i, j} 2 H
<latexit sha1_base64="uill+i5iJhtHTNliX981DcNI50A=">AAAHpXicfVVdb9s2FFW6Le60j6br417YBd6GTnbsFFmaAQECrCjarcGy2UkKhIZHSVcWY4rSSKqxQ+i/7W/sbT9ll1a8WE42ApIo8p5zeD9IhoXg2vR6f208+ODDjzZbDz/2P/n0s88fbT3+4kznpYrgNMpFrt6FTIPgEk4NNwLeFQpYFgo4D6c/uvnz96A0z+XQzAsYZWwiecIjZnBovHV9Orb8siKHPg1hwqWNkExX/tmYk+/I2fgS31CbfE2o5QG5pBWhMjdckteE0obleW15L8TZ+xRkvJQYb233ur1FI3c7/ZvO9lFv9tOfnuedjB9vPqFxHpUZSBMJpvVFv1eYkWXK8EhA5dNSQ8GiKZvABXYly0CP7CJIFWnjSEySXOEjDVmM+qsQ5FFs3mCxhoWlYGrWHA3zfIoz6IPf1DTJi5HlsigNyKiWTEpBTE5c7EnMFURGzElT1/DpdSB5BIliUcAynTGTBgV36wzM9LozUaxIg4xNIQIhbofqVTm44KFiau5cyK90ECLzROWljHVQMGNASY14o/gs0CkrQAcJN0HEROT+Y4cpRG4ypqb6v1i7GRiGk4vICTB2WCYGfoO4sgripy96T0OBuqsWJoWJApCVXXyczVXKDazZhKKEyrr3ioXfJqkxhf5hZ8fArKsNcsMsSpmcQDfKs50/StCuiPVO//u9g92DHQ0Zx1oPsbSzzhU3acc50eGyE+KOALWwe76/XX986gLKcMe4+Ph0IvKQCYq/1MGOQOpSwVGcCyyAI9wvUR7DIVUg2GyJzXHxzSK6GPZH1iXOFUAjyyfDAZMuuAokXKEDGcO9QBOWcTGPIWGlMJWlOln2m0WiE1cVld9eFdOYQYgPe92DIMo4imJZCCx5FDAznTiKppPITaWZOaqjGmz1swvca3ujat2pl4CbTMFgnoW5eIUu2ZpFV/aX47eVlU4i45XNKstxuXQA5j5jHIjXIeEN5EbDAQZliOk0pUvp/QLrCoNXxy4kS4FhvxE+G84qq8WtiDOu0fYNWroYMFGkrLpd6u9v1qIeTwTwKO3Usb9vBhOt8Xhpng+Zo1nNcjbgkwyVaF1Vjs7SMLO0Hq/ulEX2Fs/w+D7EzUTVlHhGZyFTF1h8NA3zmaXv3bvt01SVAkgKfJIaPF339wpD2mSYAmGRKZkgCPPpFE+IXnd3D2Ztsmxt8hLvHyYjICGYK9y/zpagGNGLMPq1VNsnZEHQ6XX7kLWX6EGaK4wOlxOSS4JFRQQkhmgeg0Os+LXdr/4lwQvg+f+SqIUnC5bKRQGvkf76pXG3c7bb7ePyfsX75Gevbg+9L72vvG+9vrfvHXmvvRPv1Iu8vzc2Nx5tbLW+aR23hq2z2vTBxg3middorfE/ONercw==</latexit><latexit sha1_base64="o0U6mUy1kMV0hWl5opttKZF0L1E=">AAAHpXicfVXdbts2FFa6Le60n6br5W7YBd6GznbsFFmaAQEMrCjatcGy2UkKhIZLSUcWY4rSSKqxQ+iZ9ha72wPsbo+yQyteLCcbAUkUeb7v4/khGeSCa9Pt/rVx74MPP9ps3P/Y/+TTzz5/sPXwi1OdFSqEkzATmXobMA2CSzgx3Ah4mytgaSDgLJj+6ObP3oPSPJNDM89hlLKJ5DEPmcGh8dbVydjyi5Ic+jSACZc2RDJd+qdjTr4jp+MLfENl8jWhlrfIBS0JlZnhkrwklNYszyrLOyHO3qcgo6XEeGu72+kuGrnd6V13tvvd2U9//Pn76+Pxw81HNMrCIgVpQsG0Pu91czOyTBkeCih9WmjIWThlEzjHrmQp6JFdBKkkTRyJSJwpfKQhi1F/FYI8is1rLNawoBBMzeqjQZZNcQZ98OuaJn42slzmhQEZVpJxIYjJiIs9ibiC0Ig5qesaPr1qSR5CrFjYYqlOmUlaOXfrbJnpVXuiWJ60UjaFEIS4GapW5eCCB4qpuXMhu9StAJknKitkpFs5MwaU1Ig3is9aOmE56FbMTStkInT/kcPkIjMpU1P9X6ydFAzDyUXkBBg7LGIDv0JUWgXR42fdx4FA3VULk8BEAcjSLj7O5jLhBtZsAlFAad17xcJvksSYXP+ws2Ng1tEGuWEWJkxOoBNm6c5vBWhXxHqn9/3ewe7BjoaUY60HWNpp+5KbpO2caHPZDnBHgFrYPd3frj4+dQFluGNcfHw6EVnABMVf6mB9kLpQ0I8ygQXQx/0SZhEcUgWCzZbYDBdfL6LzYW9kXeJcAdSyfDwcMOmCq0DCJTqQMtwLNGYpF/MIYlYIU1qq42W/XiQ6dlVR+s1VMY0ZhOiw2zlohSlHUSwLgSWPAmamY0dRdxK5qTQzR9WvwFY/Oce9tjcq1516DrjJFAzmaZCJF+iSrVh0aX8+elNa6SRSXtq0tByXSwdg7jLGgWgdElxDrjUcYFAEmE5TuJTeLbCuMHhx5EKyFBj2auGzway0WtyIOOMKbV+hpYsBE3nCypulvnu1FvVoIoCHSbuK/V0zmGiNx0v9fEgdzWqW0wGfpKhEq6pydJYGqaXVeHmrLNI3eIZHdyGuJ8q6xBM6C5g6x+KjSZDNLH3v3k2fJqoQQBLgk8Tg6bq/lxvSJMMECAtNwQRBmE+neEJ0O7t7MGuSZWuS53j/MBkCCcBc4v51tgTFiF6E0a+kmj4hC4J2t9ODtLlED5JMYXS4nJBMEiwqIiA2RPMIHGLFr+1e+S8JXgBP/5dELTxZsJQuCniN9NYvjdud091OD5f3C94nr72q3fe+9L7yvvV63r7X9156x96JF3p/b2xuPNjYanzTOGoMG6eV6b2Na8wjr9Ya438AGdGtQA==</latexit><latexit sha1_base64="o0U6mUy1kMV0hWl5opttKZF0L1E=">AAAHpXicfVXdbts2FFa6Le60n6br5W7YBd6GznbsFFmaAQEMrCjatcGy2UkKhIZLSUcWY4rSSKqxQ+iZ9ha72wPsbo+yQyteLCcbAUkUeb7v4/khGeSCa9Pt/rVx74MPP9ps3P/Y/+TTzz5/sPXwi1OdFSqEkzATmXobMA2CSzgx3Ah4mytgaSDgLJj+6ObP3oPSPJNDM89hlLKJ5DEPmcGh8dbVydjyi5Ic+jSACZc2RDJd+qdjTr4jp+MLfENl8jWhlrfIBS0JlZnhkrwklNYszyrLOyHO3qcgo6XEeGu72+kuGrnd6V13tvvd2U9//Pn76+Pxw81HNMrCIgVpQsG0Pu91czOyTBkeCih9WmjIWThlEzjHrmQp6JFdBKkkTRyJSJwpfKQhi1F/FYI8is1rLNawoBBMzeqjQZZNcQZ98OuaJn42slzmhQEZVpJxIYjJiIs9ibiC0Ig5qesaPr1qSR5CrFjYYqlOmUlaOXfrbJnpVXuiWJ60UjaFEIS4GapW5eCCB4qpuXMhu9StAJknKitkpFs5MwaU1Ig3is9aOmE56FbMTStkInT/kcPkIjMpU1P9X6ydFAzDyUXkBBg7LGIDv0JUWgXR42fdx4FA3VULk8BEAcjSLj7O5jLhBtZsAlFAad17xcJvksSYXP+ws2Ng1tEGuWEWJkxOoBNm6c5vBWhXxHqn9/3ewe7BjoaUY60HWNpp+5KbpO2caHPZDnBHgFrYPd3frj4+dQFluGNcfHw6EVnABMVf6mB9kLpQ0I8ygQXQx/0SZhEcUgWCzZbYDBdfL6LzYW9kXeJcAdSyfDwcMOmCq0DCJTqQMtwLNGYpF/MIYlYIU1qq42W/XiQ6dlVR+s1VMY0ZhOiw2zlohSlHUSwLgSWPAmamY0dRdxK5qTQzR9WvwFY/Oce9tjcq1516DrjJFAzmaZCJF+iSrVh0aX8+elNa6SRSXtq0tByXSwdg7jLGgWgdElxDrjUcYFAEmE5TuJTeLbCuMHhx5EKyFBj2auGzway0WtyIOOMKbV+hpYsBE3nCypulvnu1FvVoIoCHSbuK/V0zmGiNx0v9fEgdzWqW0wGfpKhEq6pydJYGqaXVeHmrLNI3eIZHdyGuJ8q6xBM6C5g6x+KjSZDNLH3v3k2fJqoQQBLgk8Tg6bq/lxvSJMMECAtNwQRBmE+neEJ0O7t7MGuSZWuS53j/MBkCCcBc4v51tgTFiF6E0a+kmj4hC4J2t9ODtLlED5JMYXS4nJBMEiwqIiA2RPMIHGLFr+1e+S8JXgBP/5dELTxZsJQuCniN9NYvjdud091OD5f3C94nr72q3fe+9L7yvvV63r7X9156x96JF3p/b2xuPNjYanzTOGoMG6eV6b2Na8wjr9Ya438AGdGtQA==</latexit><latexit sha1_base64="bE4rKKNbse4HdLdRb6Qr+Z8ywLc=">AAAHpXicfVVdb9s2FFW6re60j6br417YBd6GTnbsFFmaAQEMrCharMGy2UkKhIZHSVcWY4rSSKqxQ+iH7m0/ZZeWvVhJNgKSKPKec3g/SIaF4Nr0en9tPfjo408eth596n/2+RdfPt5+8tWZzksVwWmUi1y9D5kGwSWcGm4EvC8UsCwUcB7Ofnbz5x9AaZ7LkVkUMM7YVPKER8zg0GT7+nRi+WVFjnwawpRLGyGZrvyzCSc/kLPJJb6hNvmWUMsDckkrQmVuuCRvCKUNy/Pa8l6Is/cpyHgtMdne6XV7y0budvqrzo63aieTJw+f0jiPygykiQTT+qLfK8zYMmV4JKDyaamhYNGMTeECu5JloMd2GaSKtHEkJkmu8JGGLEf9TQjyKLZosFjDwlIwNW+Ohnk+wxn0wW9qmuTl2HJZlAZkVEsmpSAmJy72JOYKIiMWpKlr+Ow6kDyCRLEoYJnOmEmDgrt1BmZ23ZkqVqRBxmYQgRA3Q/WqHFzwUDG1cC7kVzoIkXmq8lLGOiiYMaCkRrxRfB7olBWgg4SbIGIicv+xwxQiNxlTM/1frN0MDMPJZeQEGDsqEwO/Q1xZBfGzl71noUDdTQuTwlQByMouP87mKuUGbtmEooTKuveGhd8mqTGF/ml318C8qw1ywzxKmZxCN8qz3T9L0K6I9W7/x/3DvcNdDRnHWg+xtLPOFTdpxznR4bIT4o4AtbR7cbBTf3zqAspwx7j4+HQq8pAJir/UwQYgdalgEOcCC2CA+yXKYziiCgSbr7E5Lr5ZRBej/ti6xLkCaGT5ZDRk0gVXgYQrdCBjuBdowjIuFjEkrBSmslQn636zSHTiqqLy25tiGjMI8VGvexhEGUdRLAuBJY8CZq4TR9F0ErmpNHNHNajBVj+/wL22P65uO/UKcJMpGC6yMBev0SVbs+jK/nr8rrLSSWS8slllOS6XDsHcZ4wD8W1IuIKsNBxgWIaYTlO6lN4vcFth+PrYhWQtMOo3wmfDeWW1uBFxxjXavkVLFwMmipRVN0v94+2tqMdTATxKO3Xs75vBRGs8XprnQ+ZoNrOcDfk0QyVaV5WjszTMLK3Hqztlkb3DMzy+D7GaqJoSz+k8ZOoCi4+mYT639IN7t32aqlIASYFPU4On68F+YUibjFIgLDIlEwRhPp3hCdHr7u3DvE3WrU1e4f3DZAQkBHOF+9fZEhQjehlGv5Zq+4QsCTq9bh+y9ho9THOF0eFySnJJsKiIgMQQzWNwiA2/dvrVvyR4Abz4XxK19GTJUrko4DXSv31p3O2c7XX7uLzfejuDX1YXyiPva+8b73uv7x14A++Nd+KdepH399bDrcdb263vWsetUeusNn2wtcI89RqtNfkHXbapgQ==</latexit>
Pr[select i, j | C] / pij =
(
pipj {i, j} /2 H
pipj + qij {i, j} 2 H
pi 0,
P
i pi = 1,
P
{i,j} pij = 1, 0<latexit sha1_base64="7wnzBB8kq/kiFYDKbsnSULOu8R8=">AAAILXicfVXdbts2FLa7rem0v2a93A272MPQyY6dImu7IkCAFkWLtVg2pz+AaWSUdCQxJimVpBqnhF5ht9tb7Gl2MWDY7V5jh5bT2E42Abaow/N93+HhOWRUCm7sYPBn+8p7739wdePah8FHH3/y6WfXNz9/YYpKx/A8LkShX0XMgOAKnltuBbwqNTAZCXgZTR/4+ZdvQBteqEN7WsJEskzxlMfMoulos92mquAqAWXJgR4jEcSWdBwPj+sO6dD7FNGW3sfxg84k6NBSF6UtgvLI8eOa7AU0gowrF2MMpg5oxqRkpDzi5dEx+YpQJCLHtCaoYrkijwmla07fkNcN17L3O1dQyYK7g9/e1EEcoRmQQSek9zFEU0kkqL15jwyXjZ4P6eqzYN/NNgE0JMHR9a1BfzB/yMXBcDHYai2eg6PNqzdoUsSVxKTFghkzHg5KO3FMWx4LwCxUBkoWT1kGYxwqJsFM3HyzatJFS0LSQuMPkz63BssQ5NHsdIXFWRZVgunZqjUqiinOYN6DVU2b3p04rsrKgoobybQSxBbE1wBJuMZdFqdkVdfy6dtQ8RhSzeKQSSOZzcOS+zhDO33byzQr81CyKcQgxLmpicrDBY8006d+CcWJCSNkznRRqcSEJbMWtDKIt5rPQpOzEkyYchvGTMT+O/GYUhRWMj01/8Xal2AZTs4zJ8C6wyq18BMktdOQ3Lw7uBkJ1F32sDlkGkDVbv7yPic5t7DmE4kKauf/lzyCLsmtLc1329sWZn1jkRtmcc5UBv24kNuvKzC+mcz28Nvdezv3tg1Ijl0TYYvJ3gm3ec8vosdVL8LOBD33u31nq3kF1CeUYef6/GBziCJiguIn9bB9UKbSsJ8UAgtgH/s2LhLYoxoEm51hCwx+tYjGh8OJ8xvnC2Bllw8OR0z55GpQcIILkAx7jKZMcnGaQMoqYWtHTXo2Xi0Sk/qqqIPuspjBHYRkb9C/F8aSoyiWhcCSRwE7M6mnWF0kclNlZ55qvwE7c2uMvbY7qdcX9RCwyTSMTmVUiEe4JNewmNr98Oxp7ZSXkLx2snYcw6UjsJc5oyFZh0QLyELDA0ZVhNtpK7+llwusK4wePfMpORM4HK6kz0Wz2hlxLuKdG7R7gp4+B0yUOavPQ/35yVrWk0wAj/Nek/vLZnCjDR4vq+eD9DTLuyxHPJOoRJuq8nSORtLRxl5fKAv5FO+S5DLEYqJelbhFZxHTYyw+mkfFzNE3/r8b0FxXAkgOPMstnq53dktLuuQwB8JiWzFBEBbQKZ4Qg/7OLsy65Ozpkod4DzIVA4nAnmD/el+CYsTM0xg0Ut2AkDlBb9AfguyeoUd5oTE7XGWkUASLighILTE8AY9YWtfWsH5HghfA7f8l0fOVzFlqnwW8Robrl8bFwYud/hDD+3Fna//7xYVyrfVF68vW161h605rv/W4ddB63orbefuX9q/t3zZ+3/hj46+NvxvXK+0F5kZr5dn451+8atkM</latexit><latexit sha1_base64="7wnzBB8kq/kiFYDKbsnSULOu8R8=">AAAILXicfVXdbts2FLa7rem0v2a93A272MPQyY6dImu7IkCAFkWLtVg2pz+AaWSUdCQxJimVpBqnhF5ht9tb7Gl2MWDY7V5jh5bT2E42Abaow/N93+HhOWRUCm7sYPBn+8p7739wdePah8FHH3/y6WfXNz9/YYpKx/A8LkShX0XMgOAKnltuBbwqNTAZCXgZTR/4+ZdvQBteqEN7WsJEskzxlMfMoulos92mquAqAWXJgR4jEcSWdBwPj+sO6dD7FNGW3sfxg84k6NBSF6UtgvLI8eOa7AU0gowrF2MMpg5oxqRkpDzi5dEx+YpQJCLHtCaoYrkijwmla07fkNcN17L3O1dQyYK7g9/e1EEcoRmQQSek9zFEU0kkqL15jwyXjZ4P6eqzYN/NNgE0JMHR9a1BfzB/yMXBcDHYai2eg6PNqzdoUsSVxKTFghkzHg5KO3FMWx4LwCxUBkoWT1kGYxwqJsFM3HyzatJFS0LSQuMPkz63BssQ5NHsdIXFWRZVgunZqjUqiinOYN6DVU2b3p04rsrKgoobybQSxBbE1wBJuMZdFqdkVdfy6dtQ8RhSzeKQSSOZzcOS+zhDO33byzQr81CyKcQgxLmpicrDBY8006d+CcWJCSNkznRRqcSEJbMWtDKIt5rPQpOzEkyYchvGTMT+O/GYUhRWMj01/8Xal2AZTs4zJ8C6wyq18BMktdOQ3Lw7uBkJ1F32sDlkGkDVbv7yPic5t7DmE4kKauf/lzyCLsmtLc1329sWZn1jkRtmcc5UBv24kNuvKzC+mcz28Nvdezv3tg1Ijl0TYYvJ3gm3ec8vosdVL8LOBD33u31nq3kF1CeUYef6/GBziCJiguIn9bB9UKbSsJ8UAgtgH/s2LhLYoxoEm51hCwx+tYjGh8OJ8xvnC2Bllw8OR0z55GpQcIILkAx7jKZMcnGaQMoqYWtHTXo2Xi0Sk/qqqIPuspjBHYRkb9C/F8aSoyiWhcCSRwE7M6mnWF0kclNlZ55qvwE7c2uMvbY7qdcX9RCwyTSMTmVUiEe4JNewmNr98Oxp7ZSXkLx2snYcw6UjsJc5oyFZh0QLyELDA0ZVhNtpK7+llwusK4wePfMpORM4HK6kz0Wz2hlxLuKdG7R7gp4+B0yUOavPQ/35yVrWk0wAj/Nek/vLZnCjDR4vq+eD9DTLuyxHPJOoRJuq8nSORtLRxl5fKAv5FO+S5DLEYqJelbhFZxHTYyw+mkfFzNE3/r8b0FxXAkgOPMstnq53dktLuuQwB8JiWzFBEBbQKZ4Qg/7OLsy65Ozpkod4DzIVA4nAnmD/el+CYsTM0xg0Ut2AkDlBb9AfguyeoUd5oTE7XGWkUASLighILTE8AY9YWtfWsH5HghfA7f8l0fOVzFlqnwW8Robrl8bFwYud/hDD+3Fna//7xYVyrfVF68vW161h605rv/W4ddB63orbefuX9q/t3zZ+3/hj46+NvxvXK+0F5kZr5dn451+8atkM</latexit><latexit sha1_base64="7wnzBB8kq/kiFYDKbsnSULOu8R8=">AAAILXicfVXdbts2FLa7rem0v2a93A272MPQyY6dImu7IkCAFkWLtVg2pz+AaWSUdCQxJimVpBqnhF5ht9tb7Gl2MWDY7V5jh5bT2E42Abaow/N93+HhOWRUCm7sYPBn+8p7739wdePah8FHH3/y6WfXNz9/YYpKx/A8LkShX0XMgOAKnltuBbwqNTAZCXgZTR/4+ZdvQBteqEN7WsJEskzxlMfMoulos92mquAqAWXJgR4jEcSWdBwPj+sO6dD7FNGW3sfxg84k6NBSF6UtgvLI8eOa7AU0gowrF2MMpg5oxqRkpDzi5dEx+YpQJCLHtCaoYrkijwmla07fkNcN17L3O1dQyYK7g9/e1EEcoRmQQSek9zFEU0kkqL15jwyXjZ4P6eqzYN/NNgE0JMHR9a1BfzB/yMXBcDHYai2eg6PNqzdoUsSVxKTFghkzHg5KO3FMWx4LwCxUBkoWT1kGYxwqJsFM3HyzatJFS0LSQuMPkz63BssQ5NHsdIXFWRZVgunZqjUqiinOYN6DVU2b3p04rsrKgoobybQSxBbE1wBJuMZdFqdkVdfy6dtQ8RhSzeKQSSOZzcOS+zhDO33byzQr81CyKcQgxLmpicrDBY8006d+CcWJCSNkznRRqcSEJbMWtDKIt5rPQpOzEkyYchvGTMT+O/GYUhRWMj01/8Xal2AZTs4zJ8C6wyq18BMktdOQ3Lw7uBkJ1F32sDlkGkDVbv7yPic5t7DmE4kKauf/lzyCLsmtLc1329sWZn1jkRtmcc5UBv24kNuvKzC+mcz28Nvdezv3tg1Ijl0TYYvJ3gm3ec8vosdVL8LOBD33u31nq3kF1CeUYef6/GBziCJiguIn9bB9UKbSsJ8UAgtgH/s2LhLYoxoEm51hCwx+tYjGh8OJ8xvnC2Bllw8OR0z55GpQcIILkAx7jKZMcnGaQMoqYWtHTXo2Xi0Sk/qqqIPuspjBHYRkb9C/F8aSoyiWhcCSRwE7M6mnWF0kclNlZ55qvwE7c2uMvbY7qdcX9RCwyTSMTmVUiEe4JNewmNr98Oxp7ZSXkLx2snYcw6UjsJc5oyFZh0QLyELDA0ZVhNtpK7+llwusK4wePfMpORM4HK6kz0Wz2hlxLuKdG7R7gp4+B0yUOavPQ/35yVrWk0wAj/Nek/vLZnCjDR4vq+eD9DTLuyxHPJOoRJuq8nSORtLRxl5fKAv5FO+S5DLEYqJelbhFZxHTYyw+mkfFzNE3/r8b0FxXAkgOPMstnq53dktLuuQwB8JiWzFBEBbQKZ4Qg/7OLsy65Ozpkod4DzIVA4nAnmD/el+CYsTM0xg0Ut2AkDlBb9AfguyeoUd5oTE7XGWkUASLighILTE8AY9YWtfWsH5HghfA7f8l0fOVzFlqnwW8Robrl8bFwYud/hDD+3Fna//7xYVyrfVF68vW161h605rv/W4ddB63orbefuX9q/t3zZ+3/hj46+NvxvXK+0F5kZr5dn451+8atkM</latexit><latexit sha1_base64="7wnzBB8kq/kiFYDKbsnSULOu8R8=">AAAILXicfVXdbts2FLa7rem0v2a93A272MPQyY6dImu7IkCAFkWLtVg2pz+AaWSUdCQxJimVpBqnhF5ht9tb7Gl2MWDY7V5jh5bT2E42Abaow/N93+HhOWRUCm7sYPBn+8p7739wdePah8FHH3/y6WfXNz9/YYpKx/A8LkShX0XMgOAKnltuBbwqNTAZCXgZTR/4+ZdvQBteqEN7WsJEskzxlMfMoulos92mquAqAWXJgR4jEcSWdBwPj+sO6dD7FNGW3sfxg84k6NBSF6UtgvLI8eOa7AU0gowrF2MMpg5oxqRkpDzi5dEx+YpQJCLHtCaoYrkijwmla07fkNcN17L3O1dQyYK7g9/e1EEcoRmQQSek9zFEU0kkqL15jwyXjZ4P6eqzYN/NNgE0JMHR9a1BfzB/yMXBcDHYai2eg6PNqzdoUsSVxKTFghkzHg5KO3FMWx4LwCxUBkoWT1kGYxwqJsFM3HyzatJFS0LSQuMPkz63BssQ5NHsdIXFWRZVgunZqjUqiinOYN6DVU2b3p04rsrKgoobybQSxBbE1wBJuMZdFqdkVdfy6dtQ8RhSzeKQSSOZzcOS+zhDO33byzQr81CyKcQgxLmpicrDBY8006d+CcWJCSNkznRRqcSEJbMWtDKIt5rPQpOzEkyYchvGTMT+O/GYUhRWMj01/8Xal2AZTs4zJ8C6wyq18BMktdOQ3Lw7uBkJ1F32sDlkGkDVbv7yPic5t7DmE4kKauf/lzyCLsmtLc1329sWZn1jkRtmcc5UBv24kNuvKzC+mcz28Nvdezv3tg1Ijl0TYYvJ3gm3ec8vosdVL8LOBD33u31nq3kF1CeUYef6/GBziCJiguIn9bB9UKbSsJ8UAgtgH/s2LhLYoxoEm51hCwx+tYjGh8OJ8xvnC2Bllw8OR0z55GpQcIILkAx7jKZMcnGaQMoqYWtHTXo2Xi0Sk/qqqIPuspjBHYRkb9C/F8aSoyiWhcCSRwE7M6mnWF0kclNlZ55qvwE7c2uMvbY7qdcX9RCwyTSMTmVUiEe4JNewmNr98Oxp7ZSXkLx2snYcw6UjsJc5oyFZh0QLyELDA0ZVhNtpK7+llwusK4wePfMpORM4HK6kz0Wz2hlxLuKdG7R7gp4+B0yUOavPQ/35yVrWk0wAj/Nek/vLZnCjDR4vq+eD9DTLuyxHPJOoRJuq8nSORtLRxl5fKAv5FO+S5DLEYqJelbhFZxHTYyw+mkfFzNE3/r8b0FxXAkgOPMstnq53dktLuuQwB8JiWzFBEBbQKZ4Qg/7OLsy65Ozpkod4DzIVA4nAnmD/el+CYsTM0xg0Ut2AkDlBb9AfguyeoUd5oTE7XGWkUASLighILTE8AY9YWtfWsH5HghfA7f8l0fOVzFlqnwW8Robrl8bFwYud/hDD+3Fna//7xYVyrfVF68vW161h605rv/W4ddB63orbefuX9q/t3zZ+3/hj46+NvxvXK+0F5kZr5dn451+8atkM</latexit>

28. Other set sizes have the same utility structure.
28
Same base utilities Same collection of “special sets”
Uijk =
(
Vi + Vj + Vk + eijk {i, j, k} /2 H
Vi + Vj + Vk + Wijk + eijk {i, j, k} 2 H
<latexit sha1_base64="A7/nkIHflRU2bAqBmczP19ozDzU=">AAAHu3icfVXrbts2FFa6re60W7r+3H6wC1wMnezYKbI0AwIYWFG0W4tlcy4FQsOjpCOLMUVpJNXYJfQOe6S9xl5kv3do2YvlpCNgiibP9308F5JhIbg2vd7fW3c++PCju617H/uffPrZ519s3//yTOeliuA0ykWu3oRMg+ASTg03At4UClgWCjgPpz+69fO3oDTP5YmZFzDK2ETyhEfM4NR4+8/TseWX04oc+TSECZc2QjZd+WdjTr4jZ+PLRT/FHpaWjwi1PCCXAZnSilCZGy7JC0LpLZjzJea9aAf1Kch4pTve3ul1e4tGbg76y8HOoDf76S/P847H9+8+oHEelRlIEwmm9UW/V5iRZcrwSEDl01JDwaIpm8AFDiXLQI/sInQVaeNMTJJc4U8aspj11yHIo9i8wWINC0vB1Kw5G+b5FFfQB7+paZKnI8tlURqQUS2ZlIKYnLiMkJgriIyYk6au4dN3geQRJIpFAct0xkwaFNztMzDTd52JYkUaZGwKEQhxPVXvysEFDxVTc+dCfqWDEJknKi9lrIOCGQNKasQbxWeBTlkBOki4CSImIvc/dphC5CZjaqrfx9rNwDBcXEROgLEnZWLgN4grqyB++LT3MBSou25hUpgoAFnZxcfZXKXcwIZNKEqorOvXLPw2SY0p9A+7uwZmXW2QG2ZRyuQEulGe7f5RgnalrXf73+8f7h3uasg4noAQCz7rXHGTdpwTHS47IZ4TUAu7Jwc79cenLqAMz5GLj08nIg+ZoPiXOtgApC4VDOJcYAEM8BRFeQxHVIFgsxU2x803i+jipD+yLnGuABpZPj4ZMumCq0DCFTqQMTwLNGEZF/MYElYKU1mqk9W4WSQ6cVVR+e11MY0ZhPio1z0MooyjKJaFwJJHATPTiaNoOoncVJqZoxrUYKsfX+BZ2x9Vm049AzxkCobzLMzFc3TJ1iy6sr+8flVZ6SQyXtmsshy3S4dgbjPGiXgTEi4hSw0HGJYhptOULqW3C2wqDJ+/diFZCZz0G+Gz4ayyWlyLOOMabV+ipYsBE0XKquut/v5yI+rxRACP0k4d+9tWMNEar5fm/ZA5mvUsZ0M+yVCJ1lXl6CwNM0vr+epGWWSv8GaPb0MsF6qmxGM6C5m6wOKjaZjPLH3r+rZPU1UKICnwSWrwdj3YLwxpk5MUCItMyQRBmE+neEP0unv7MGuTVWuTZ/gqMRkBCcFc4fl1tgTFiF6E0a+l2j4hC4JOr9uHrL1CD9NcYXS4nJBcEiwqIiAxRPMYHGLNr51+9R8JPgBP/pdELTxZsFQuCviM9DcfjZuDs71uH7f3K74nP3t1u+d95X3jfev1vQNv4L3wjr1TL/L+2fp6q731qHXUilqXLVGb3tlaYh54jdYq/wVM3LJ/</latexit><latexit sha1_base64="+4oQQEukkDPEdeN44Q/oWEI89E4=">AAAHu3icfVXdbts2FFa6re60n6br5XbBLnAxdLJjp8jSDAhgYEXRri2WzU5SIDQ8SjqSGFOURlKNXULvsDfZW+xuD7AX2fUO/bPYTjoCpmjyfN/H80MyLAXXptP5e+vWBx9+dLtx52P/k08/+/zu9r0vTnVRqQhOokIU6k3INAgu4cRwI+BNqYDloYCzcPyDWz97C0rzQg7MtIRhzlLJEx4xg1Oj7d9PRpZfjGty5NMQUi5thGy69k9HnHxLTkcXs36MPSwsHxJqeUAuAjKmNaGyMFyS54TSGzBnC8x70Q7qU5DxUne0vdNpd2aNXB90F4OdXmfy459//fHyeHTv9n0aF1GVgzSRYFqfdzulGVqmDI8E1D6tNJQsGrMUznEoWQ56aGehq0kTZ2KSFAp/0pDZrL8KQR7Fpmss1rCwEkxN1mfDohjjCvrgr2ua5MnQcllWBmQ0l0wqQUxBXEZIzBVERkzJuq7h43eB5BEkikUBy3XOTBaU3O0zMON3rVSxMgtyNoYIhLiamu/KwQUPFVNT50JxqYMQmVNVVDLWQcmMASU14o3ik0BnrAQdJNwEEROR+x87TCkKkzM11u9jbedgGC7OIifA2EGVGPgF4toqiB886TwIBequWpgMUgUgazv7OJvLjBvYsAlFBbV1/YqF3ySZMaX+fnfXwKStDXLDJMqYTKEdFfnubxVoV9p6t/vd/uHe4a6GnOMJCLHg89YlN1nLOdHishXiOQE1s3t8sDP/+NQFlOE5cvHxaSqKkAmKf6mD9UDqSkEvLgQWQA9PUVTEcEQVCDZZYgvc/HoRnQ+6Q+sS5wpgLcvHgz6TLrgKJFyiAznDs0ATlnMxjSFhlTC1pTpZjteLRCeuKmq/uSqmMYMQH3Xah0GUcxTFshBY8ihgJjpxFOtOIjeVZuKoenOw1Y/O8aztD+tNp54CHjIF/WkeFuIZumTnLLq2P71+VVvpJHJe27y2HLdL+2BuMsaJeBMSLiALDQfoVyGm01QupTcLbCr0n712IVkKDLpr4bPhpLZaXIk44znavkBLFwMmyozVV1v99cVG1ONUAI+y1jz2N61gojVeL+v3Q+5oVrOc93maoxKdV5WjszTMLZ3P19fKIn+FN3t8E2KxUK9LPKKTkKlzLD6ahcXE0reub/o0U5UAkgFPM4O368F+aUiTDDIgLDIVEwRhPh3jDdFp7+3DpEmWrUme4qvEZAQkBHOJ59fZEhQjehZGfy7V9AmZEbQ67S7kzSW6nxUKo8NlSgpJsKiIgMQQzWNwiBW/drr1fyT4ADz+XxI182TGUrso4DPS3Xw0rg9O99pd3N7P+J689Obtjvel97X3jdf1Drye99w79k68yPtn66ut5tbDxlEjalw0xNz01tYCc99ba43qXy3WtEw=</latexit><latexit sha1_base64="+4oQQEukkDPEdeN44Q/oWEI89E4=">AAAHu3icfVXdbts2FFa6re60n6br5XbBLnAxdLJjp8jSDAhgYEXRri2WzU5SIDQ8SjqSGFOURlKNXULvsDfZW+xuD7AX2fUO/bPYTjoCpmjyfN/H80MyLAXXptP5e+vWBx9+dLtx52P/k08/+/zu9r0vTnVRqQhOokIU6k3INAgu4cRwI+BNqYDloYCzcPyDWz97C0rzQg7MtIRhzlLJEx4xg1Oj7d9PRpZfjGty5NMQUi5thGy69k9HnHxLTkcXs36MPSwsHxJqeUAuAjKmNaGyMFyS54TSGzBnC8x70Q7qU5DxUne0vdNpd2aNXB90F4OdXmfy459//fHyeHTv9n0aF1GVgzSRYFqfdzulGVqmDI8E1D6tNJQsGrMUznEoWQ56aGehq0kTZ2KSFAp/0pDZrL8KQR7Fpmss1rCwEkxN1mfDohjjCvrgr2ua5MnQcllWBmQ0l0wqQUxBXEZIzBVERkzJuq7h43eB5BEkikUBy3XOTBaU3O0zMON3rVSxMgtyNoYIhLiamu/KwQUPFVNT50JxqYMQmVNVVDLWQcmMASU14o3ik0BnrAQdJNwEEROR+x87TCkKkzM11u9jbedgGC7OIifA2EGVGPgF4toqiB886TwIBequWpgMUgUgazv7OJvLjBvYsAlFBbV1/YqF3ySZMaX+fnfXwKStDXLDJMqYTKEdFfnubxVoV9p6t/vd/uHe4a6GnOMJCLHg89YlN1nLOdHishXiOQE1s3t8sDP/+NQFlOE5cvHxaSqKkAmKf6mD9UDqSkEvLgQWQA9PUVTEcEQVCDZZYgvc/HoRnQ+6Q+sS5wpgLcvHgz6TLrgKJFyiAznDs0ATlnMxjSFhlTC1pTpZjteLRCeuKmq/uSqmMYMQH3Xah0GUcxTFshBY8ihgJjpxFOtOIjeVZuKoenOw1Y/O8aztD+tNp54CHjIF/WkeFuIZumTnLLq2P71+VVvpJHJe27y2HLdL+2BuMsaJeBMSLiALDQfoVyGm01QupTcLbCr0n712IVkKDLpr4bPhpLZaXIk44znavkBLFwMmyozVV1v99cVG1ONUAI+y1jz2N61gojVeL+v3Q+5oVrOc93maoxKdV5WjszTMLZ3P19fKIn+FN3t8E2KxUK9LPKKTkKlzLD6ahcXE0reub/o0U5UAkgFPM4O368F+aUiTDDIgLDIVEwRhPh3jDdFp7+3DpEmWrUme4qvEZAQkBHOJ59fZEhQjehZGfy7V9AmZEbQ67S7kzSW6nxUKo8NlSgpJsKiIgMQQzWNwiBW/drr1fyT4ADz+XxI182TGUrso4DPS3Xw0rg9O99pd3N7P+J689Obtjvel97X3jdf1Drye99w79k68yPtn66ut5tbDxlEjalw0xNz01tYCc99ba43qXy3WtEw=</latexit><latexit sha1_base64="buQDTxZcApTh65QDo/lLZ15HFeU=">AAAHu3icfVXtbts2FFW6re60r3T9uf1gF7gYOtmxU2RpBgQwsKJosRbrZicpEBoeJV1JjClKI6nGLqF32OvtRfZ7l/5YLCcdAVM0ec85vB8kw1JwbXq9v3fufPTxJ3db9z71P/v8iy+/2r3/9ZkuKhXBaVSIQr0NmQbBJZwabgS8LRWwPBRwHk5/duvn70BpXsiRmZcwzlkqecIjZnBqsvvX6cTyy2lNTnwaQsqljZBN1/7ZhJMfyNnkctFPsYeV5SNCLQ/IZUCmtCZUFoZL8oJQegvmfIX5INpBfQoyXutOdvd63d6ikZuD/mqw563am8n9uw9oXERVDtJEgml90e+VZmyZMjwSUPu00lCyaMpSuMChZDnosV2EriZtnIlJUij8SUMWs/4mBHkUmzdYrGFhJZiaNWfDopjiCvrgNzVN8nRsuSwrAzJaSiaVIKYgLiMk5goiI+akqWv49H0geQSJYlHAcp0zkwUld/sMzPR9J1WszIKcTSECIa6nlrtycMFDxdTcuVBc6SBE5lQVlYx1UDJjQEmNeKP4LNAZK0EHCTdBxETk/scOU4rC5ExN9YdYuzkYhouLyAkwdlQlBn6HuLYK4odPew9DgbqbFiaDVAHI2i4+zuYq4wa2bEJRQW1dv2Hht0lmTKl/2t83MOtqg9wwizImU+hGRb7/ZwXalbbe7/94eHxwvK8h53gCQiz4vHPFTdZxTnS47IR4TkAt7J4c7S0/PnUBZXiOXHx8mooiZILiX+pgA5C6UjCIC4EFMMBTFBUxnFAFgs3W2AI33yyii1F/bF3iXAE0svxmNGTSBVeBhCt0IGd4FmjCci7mMSSsEqa2VCfrcbNIdOKqovbbm2IaMwjxSa97HEQ5R1EsC4EljwJmphNH0XQSuak0M0c1WIKtfnyBZ+1wXG879QzwkCkYzvOwEM/RJbtk0bX99fWr2konkfPa5rXluF06BHObMU7E25BwBVlpOMCwCjGdpnIpvV1gW2H4/LULyVpg1G+Ez4az2mpxLeKMl2j7Ei1dDJgoM1Zfb/WPl1tRj1MBPMo6y9jftoKJ1ni9NO+H3NFsZjkf8jRHJbqsKkdnaZhbupyvb5RF/gpv9vg2xGqhbko8prOQqQssPpqFxczSd65v+zRTlQCSAU8zg7fr0WFpSJuMMiAsMhUTBGE+neIN0eseHMKsTdatTZ7hq8RkBCQEc4Xn19kSFCN6EUZ/KdX2CVkQdHrdPuTtNXqYFQqjw2VKCkmwqIiAxBDNY3CIDb/2+vV/JPgAPPlfErXwZMFSuyjgM9LffjRuDs4Oun3c3m+9vcEvqwflnveN9533vdf3jryB98J74516kffPzrc77Z1HrZNW1LpsiaXpnZ0V5oHXaK3qX3G7sI0=</latexit>
Pr[select {i, j, k} | C] / pijk =
(
pipjpk {i, j, k} /2 H
pipjpk + qijk {i, j, k} 2 H
pi 0,
P
i pi = 1,
P
{i,j,k} pijk = 1, 3 0<latexit sha1_base64="YDzigRxzN2zUm63fepEQEC5wPog=">AAAIRHicfVXdbts2FLa7rem0v3a9GbAbdrGHoZMdO0GWZkGAAC2KFmuxbE5/gNDwKOlIYkxSKkk1TglhT7Pb7S32DnuH3Q27HXZoO6ntZBNgizo63/cdnh8xKgU3ttf7o3ntnXffu7524/3ggw8/+viTm7c+fW6KSsfwLC5EoV9GzIDgCp5ZbgW8LDUwGQl4EY3v+/cvXoM2vFBH9qyEoWSZ4imPmUXT6FbzM6oKrhJQlhzqYySC2JIWdTw8Cce0buF6jyKDpXu4vt8aBi1a6qK0RVCOHD8Z12Q/oBFkXLkYAzF1QDMmJSPliJejk3I0Jl8Sz0dOQoKMBAUtV+QRofSy69fk1Zx1BXSBAJXMhVr47E0thBOaAem1QrqHAZtKIkntzfukv2i82Fd9EfyFwzSU0dacKRjdXO91e9OLXF7054v1xvw6HN26fpsmRVxJzGUsmDHH/V5ph45py2MBmJfKQMniMcvgGJeKSTBDN61hTdpoSUhaaPxhLabWYBGCPJqdLbE4y6JKMD1ZtkZFMcY3WIlgWdOm94aOq7KyoOKZZFoJYgviW4MkXGPxxRlZ1rV8/CZUPIZUszhk0khm87DkPs7Qjt90Ms3KPJRsDDEI8dY0i8rDBY8002d+C8WpCSNkznRRqcSEJbMWtDKIt5pPQpOzEkyYchvGTMT+OfGYUhRWMj02/8XalWAZvpxmToB1R1Vq4UdIaqchuXOvdycSqLvoYXPINICq3fTmfU5zbmHFJxIV1M7/L3gEbZJbW5pvNzYsTLrGIjdM4pypDLpxITdeVWD8jJmN/jfbu5u7GwYkx0GKcPJk55TbvOM30eGqE+HAgp76be2sz24B9QllONA+PzgoooiYoPhIPewAlKk0HCSFwAY4wHGOiwT2qQbBJufYAoNfbqLjo/7Q+cL5Bliq8uHRgCmfXA0KTnEDkuGg0ZRJLs4SSFklbO2oSc/Xy01iUt8VddBeFDNYQUj2e93dMJYcRbEtBLY8CtiJST3F8iaRmyo78VQHM7Azd49x1raH9eqmHgAOmYbBmYwK8RC35GYspnbfP31SO+UlJK+drB3HcOkA7FXOaEhWIdEcMtfwgEEVYTlt5Ut6tcCqwuDhU5+Sc4Gj/lL6XDSpnRFvRbzzDO0eo6fPARNlzuq3of70eCXrSSaAx3lnlvur3mChDX5elr8P0tMsVlkOeCZRic66ytM5GklHZ/b6UlvIJ3jEJFch5i/qZYm7dBIxfYzNR/OomDj62v+3A5rrSgDJgWe5xa/rznZpSZsc5UBYbCsmCMICOsYvRK+7uQ2TNjm/2uQBHo9MxUAisKc4v96XoBgx0zQGM6l2QMiUoNPr9kG2z9GDvNCYHa4yUiiCTUUEpJYYnoBHLOxrvV9fkOABsPW/JHq6kylL7bOAx0h/9dC4vHi+2e1jeD9srh98Nz9QbjQ+b3zR+KrRb+w0DhqPGoeNZ424+XPzl+avzd/Wfl/7c+2vtb9nrteac8ztxtK19s+/RCXhjQ==</latexit><latexit sha1_base64="YDzigRxzN2zUm63fepEQEC5wPog=">AAAIRHicfVXdbts2FLa7rem0v3a9GbAbdrGHoZMdO0GWZkGAAC2KFmuxbE5/gNDwKOlIYkxSKkk1TglhT7Pb7S32DnuH3Q27HXZoO6ntZBNgizo63/cdnh8xKgU3ttf7o3ntnXffu7524/3ggw8/+viTm7c+fW6KSsfwLC5EoV9GzIDgCp5ZbgW8LDUwGQl4EY3v+/cvXoM2vFBH9qyEoWSZ4imPmUXT6FbzM6oKrhJQlhzqYySC2JIWdTw8Cce0buF6jyKDpXu4vt8aBi1a6qK0RVCOHD8Z12Q/oBFkXLkYAzF1QDMmJSPliJejk3I0Jl8Sz0dOQoKMBAUtV+QRofSy69fk1Zx1BXSBAJXMhVr47E0thBOaAem1QrqHAZtKIkntzfukv2i82Fd9EfyFwzSU0dacKRjdXO91e9OLXF7054v1xvw6HN26fpsmRVxJzGUsmDHH/V5ph45py2MBmJfKQMniMcvgGJeKSTBDN61hTdpoSUhaaPxhLabWYBGCPJqdLbE4y6JKMD1ZtkZFMcY3WIlgWdOm94aOq7KyoOKZZFoJYgviW4MkXGPxxRlZ1rV8/CZUPIZUszhk0khm87DkPs7Qjt90Ms3KPJRsDDEI8dY0i8rDBY8002d+C8WpCSNkznRRqcSEJbMWtDKIt5pPQpOzEkyYchvGTMT+OfGYUhRWMj02/8XalWAZvpxmToB1R1Vq4UdIaqchuXOvdycSqLvoYXPINICq3fTmfU5zbmHFJxIV1M7/L3gEbZJbW5pvNzYsTLrGIjdM4pypDLpxITdeVWD8jJmN/jfbu5u7GwYkx0GKcPJk55TbvOM30eGqE+HAgp76be2sz24B9QllONA+PzgoooiYoPhIPewAlKk0HCSFwAY4wHGOiwT2qQbBJufYAoNfbqLjo/7Q+cL5Bliq8uHRgCmfXA0KTnEDkuGg0ZRJLs4SSFklbO2oSc/Xy01iUt8VddBeFDNYQUj2e93dMJYcRbEtBLY8CtiJST3F8iaRmyo78VQHM7Azd49x1raH9eqmHgAOmYbBmYwK8RC35GYspnbfP31SO+UlJK+drB3HcOkA7FXOaEhWIdEcMtfwgEEVYTlt5Ut6tcCqwuDhU5+Sc4Gj/lL6XDSpnRFvRbzzDO0eo6fPARNlzuq3of70eCXrSSaAx3lnlvur3mChDX5elr8P0tMsVlkOeCZRic66ytM5GklHZ/b6UlvIJ3jEJFch5i/qZYm7dBIxfYzNR/OomDj62v+3A5rrSgDJgWe5xa/rznZpSZsc5UBYbCsmCMICOsYvRK+7uQ2TNjm/2uQBHo9MxUAisKc4v96XoBgx0zQGM6l2QMiUoNPr9kG2z9GDvNCYHa4yUiiCTUUEpJYYnoBHLOxrvV9fkOABsPW/JHq6kylL7bOAx0h/9dC4vHi+2e1jeD9srh98Nz9QbjQ+b3zR+KrRb+w0DhqPGoeNZ424+XPzl+avzd/Wfl/7c+2vtb9nrteac8ztxtK19s+/RCXhjQ==</latexit><latexit sha1_base64="YDzigRxzN2zUm63fepEQEC5wPog=">AAAIRHicfVXdbts2FLa7rem0v3a9GbAbdrGHoZMdO0GWZkGAAC2KFmuxbE5/gNDwKOlIYkxSKkk1TglhT7Pb7S32DnuH3Q27HXZoO6ntZBNgizo63/cdnh8xKgU3ttf7o3ntnXffu7524/3ggw8/+viTm7c+fW6KSsfwLC5EoV9GzIDgCp5ZbgW8LDUwGQl4EY3v+/cvXoM2vFBH9qyEoWSZ4imPmUXT6FbzM6oKrhJQlhzqYySC2JIWdTw8Cce0buF6jyKDpXu4vt8aBi1a6qK0RVCOHD8Z12Q/oBFkXLkYAzF1QDMmJSPliJejk3I0Jl8Sz0dOQoKMBAUtV+QRofSy69fk1Zx1BXSBAJXMhVr47E0thBOaAem1QrqHAZtKIkntzfukv2i82Fd9EfyFwzSU0dacKRjdXO91e9OLXF7054v1xvw6HN26fpsmRVxJzGUsmDHH/V5ph45py2MBmJfKQMniMcvgGJeKSTBDN61hTdpoSUhaaPxhLabWYBGCPJqdLbE4y6JKMD1ZtkZFMcY3WIlgWdOm94aOq7KyoOKZZFoJYgviW4MkXGPxxRlZ1rV8/CZUPIZUszhk0khm87DkPs7Qjt90Ms3KPJRsDDEI8dY0i8rDBY8002d+C8WpCSNkznRRqcSEJbMWtDKIt5pPQpOzEkyYchvGTMT+OfGYUhRWMj02/8XalWAZvpxmToB1R1Vq4UdIaqchuXOvdycSqLvoYXPINICq3fTmfU5zbmHFJxIV1M7/L3gEbZJbW5pvNzYsTLrGIjdM4pypDLpxITdeVWD8jJmN/jfbu5u7GwYkx0GKcPJk55TbvOM30eGqE+HAgp76be2sz24B9QllONA+PzgoooiYoPhIPewAlKk0HCSFwAY4wHGOiwT2qQbBJufYAoNfbqLjo/7Q+cL5Bliq8uHRgCmfXA0KTnEDkuGg0ZRJLs4SSFklbO2oSc/Xy01iUt8VddBeFDNYQUj2e93dMJYcRbEtBLY8CtiJST3F8iaRmyo78VQHM7Azd49x1raH9eqmHgAOmYbBmYwK8RC35GYspnbfP31SO+UlJK+drB3HcOkA7FXOaEhWIdEcMtfwgEEVYTlt5Ut6tcCqwuDhU5+Sc4Gj/lL6XDSpnRFvRbzzDO0eo6fPARNlzuq3of70eCXrSSaAx3lnlvur3mChDX5elr8P0tMsVlkOeCZRic66ytM5GklHZ/b6UlvIJ3jEJFch5i/qZYm7dBIxfYzNR/OomDj62v+3A5rrSgDJgWe5xa/rznZpSZsc5UBYbCsmCMICOsYvRK+7uQ2TNjm/2uQBHo9MxUAisKc4v96XoBgx0zQGM6l2QMiUoNPr9kG2z9GDvNCYHa4yUiiCTUUEpJYYnoBHLOxrvV9fkOABsPW/JHq6kylL7bOAx0h/9dC4vHi+2e1jeD9srh98Nz9QbjQ+b3zR+KrRb+w0DhqPGoeNZ424+XPzl+avzd/Wfl/7c+2vtb9nrteac8ztxtK19s+/RCXhjQ==</latexit><latexit sha1_base64="YDzigRxzN2zUm63fepEQEC5wPog=">AAAIRHicfVXdbts2FLa7rem0v3a9GbAbdrGHoZMdO0GWZkGAAC2KFmuxbE5/gNDwKOlIYkxSKkk1TglhT7Pb7S32DnuH3Q27HXZoO6ntZBNgizo63/cdnh8xKgU3ttf7o3ntnXffu7524/3ggw8/+viTm7c+fW6KSsfwLC5EoV9GzIDgCp5ZbgW8LDUwGQl4EY3v+/cvXoM2vFBH9qyEoWSZ4imPmUXT6FbzM6oKrhJQlhzqYySC2JIWdTw8Cce0buF6jyKDpXu4vt8aBi1a6qK0RVCOHD8Z12Q/oBFkXLkYAzF1QDMmJSPliJejk3I0Jl8Sz0dOQoKMBAUtV+QRofSy69fk1Zx1BXSBAJXMhVr47E0thBOaAem1QrqHAZtKIkntzfukv2i82Fd9EfyFwzSU0dacKRjdXO91e9OLXF7054v1xvw6HN26fpsmRVxJzGUsmDHH/V5ph45py2MBmJfKQMniMcvgGJeKSTBDN61hTdpoSUhaaPxhLabWYBGCPJqdLbE4y6JKMD1ZtkZFMcY3WIlgWdOm94aOq7KyoOKZZFoJYgviW4MkXGPxxRlZ1rV8/CZUPIZUszhk0khm87DkPs7Qjt90Ms3KPJRsDDEI8dY0i8rDBY8002d+C8WpCSNkznRRqcSEJbMWtDKIt5pPQpOzEkyYchvGTMT+OfGYUhRWMj02/8XalWAZvpxmToB1R1Vq4UdIaqchuXOvdycSqLvoYXPINICq3fTmfU5zbmHFJxIV1M7/L3gEbZJbW5pvNzYsTLrGIjdM4pypDLpxITdeVWD8jJmN/jfbu5u7GwYkx0GKcPJk55TbvOM30eGqE+HAgp76be2sz24B9QllONA+PzgoooiYoPhIPewAlKk0HCSFwAY4wHGOiwT2qQbBJufYAoNfbqLjo/7Q+cL5Bliq8uHRgCmfXA0KTnEDkuGg0ZRJLs4SSFklbO2oSc/Xy01iUt8VddBeFDNYQUj2e93dMJYcRbEtBLY8CtiJST3F8iaRmyo78VQHM7Azd49x1raH9eqmHgAOmYbBmYwK8RC35GYspnbfP31SO+UlJK+drB3HcOkA7FXOaEhWIdEcMtfwgEEVYTlt5Ut6tcCqwuDhU5+Sc4Gj/lL6XDSpnRFvRbzzDO0eo6fPARNlzuq3of70eCXrSSaAx3lnlvur3mChDX5elr8P0tMsVlkOeCZRic66ytM5GklHZ/b6UlvIJ3jEJFch5i/qZYm7dBIxfYzNR/OomDj62v+3A5rrSgDJgWe5xa/rznZpSZsc5UBYbCsmCMICOsYvRK+7uQ2TNjm/2uQBHo9MxUAisKc4v96XoBgx0zQGM6l2QMiUoNPr9kG2z9GDvNCYHa4yUiiCTUUEpJYYnoBHLOxrvV9fkOABsPW/JHq6kylL7bOAx0h/9dC4vHi+2e1jeD9srh98Nz9QbjQ+b3zR+KrRb+w0DhqPGoeNZ424+XPzl+avzd/Wfl/7c+2vtb9nrteac8ztxtK19s+/RCXhjQ==</latexit>
Same probabilities Different scaling factor

29. The final model factors the size and set selection.
29
Pr[select size-k set S] = zk
Pr[select set S | choice set C]
=
zk
z1 + · · · + z|C|
· Pr[select set S | choice set C, |S| = k]
<latexit sha1_base64="W7yxdQMaznTvXEOJTSOkBhZK5KA=">AAAIKHicnVXdbts2FJa7re60n6br5W7YxR6GTnbsdFmaFQEMpChWrMWy2WkLmEZGSUcWYeonJNXYIfQAu93eYk+zu6G3e48BO7Sc1XKyXYywJYrnfN9HnnNI+rngSvd6bxo33nn3vZvNW++7H3z40ce3t+588kJlhQzgJMhEJl/5TIHgKZxorgW8yiWwxBfw0p8dWfvL1yAVz9KRXuQwSdg05REPmMah062/PidUw1ybYzlGFgg0UfwCOq1ZiyjQpDVsTcghaV2czloloRR/7jWQypO06COKapo+apEgzngAlemoNSmXSHp2VrAQCWkkWWCQtcRHn3xJaBBmWmHn4tRQYUnIEaHSdsqysv4PWQ9tFdlwRYbas9VsXPd0a7vX7S0budrprzrbzqodn965eZeGWVAkkOpAMKXG/V6uJ4ZJzQMBpUsLBTkLZmwKY+ymLAE1Mcs8laSNIyGJMon/VJPlqLsOQR7JFjUWo5lfCCbn9VE/y2ZoUaXr1jV19HBieJoXGtKgkowKQXRGbPpJyCVGTixIXVfz2YWXYuBsWjyWqITp2Mu5naenZxedqWR57CVsBgEI8XaompWFC+5LJhd2Cdm58nxknsqsSEPl5UxrkKlCvJZ87qmY5aC8iGsvYCKw36HF5CLTCZMz9W+s3QQ0Q+MycgK0GRWRhh8hLI2E8N7D3j1foO66h45hKgHS0ixf1uc85ho2fHxRQGnsc83DbZNY61x9s7ODlddVGrlhHsQsnUI3yJKdswKU3Udqp//13sHuwY6ChGOV+bi7ks4513HHLqLD046PmxLk0u/B/nb1cqkNKMNNa+Pj0qnIfCYoflILG0CqCgmDMBNYAAPcskEWwiGVINj8Epvh5OtFNB71J8YmzhZALcvHoyFLbXAlpHCOC0hYGhoasYSLRQgRK4QuDVXRZb9eJCqyVVG67XUxhRmE8LDXPfCChKMoloXAkkcBPVeRpagvErlpqueWalCBjbo/xr22Nyk3F/UYcJNJGC4SPxNPcEmmYlGl+f75s9KkViLhpUlKw3G6dAj6OmccCDch/gqy0rCAYeFjOnVhU3q9wKbC8MlzG5JLgVG/Fj7jz0ujxFsR61yhzVP0tDFgIo9Z+XaqPz3diHo4FcCDuFPF/joLJlrh8VI/HxJLs57lZMinCSrRqqosnaF+Ymg1Xl4pi+QZXiPhdYiVoaxL3Kdzn8kxFh+N/Wxu6Gv7bLs0loUAEgOfxhpP1/29XJM2GcVAWKALJgjCXDrDE6LX3d2DeZtctjZ5jFcgS/FA90Gf4/61vgTFiFqG0a2k2i4hS4JOr9uHpH2JHsaZxOjwdEqylGBREQGRveFCsIi1dW33y39I8AJ48J8kcrmSJUtpo4DXSH/z0rjaebHb7eP0fvhqe/Dd6kK55XzqfOZ84fSdfWfgfOscOydO0AgaPzd+afza/K35e/OP5pvK9UZjhbnr1Frzz78BaGTZDg==</latexit><latexit sha1_base64="W7yxdQMaznTvXEOJTSOkBhZK5KA=">AAAIKHicnVXdbts2FJa7re60n6br5W7YxR6GTnbsdFmaFQEMpChWrMWy2WkLmEZGSUcWYeonJNXYIfQAu93eYk+zu6G3e48BO7Sc1XKyXYywJYrnfN9HnnNI+rngSvd6bxo33nn3vZvNW++7H3z40ce3t+588kJlhQzgJMhEJl/5TIHgKZxorgW8yiWwxBfw0p8dWfvL1yAVz9KRXuQwSdg05REPmMah062/PidUw1ybYzlGFgg0UfwCOq1ZiyjQpDVsTcghaV2czloloRR/7jWQypO06COKapo+apEgzngAlemoNSmXSHp2VrAQCWkkWWCQtcRHn3xJaBBmWmHn4tRQYUnIEaHSdsqysv4PWQ9tFdlwRYbas9VsXPd0a7vX7S0budrprzrbzqodn965eZeGWVAkkOpAMKXG/V6uJ4ZJzQMBpUsLBTkLZmwKY+ymLAE1Mcs8laSNIyGJMon/VJPlqLsOQR7JFjUWo5lfCCbn9VE/y2ZoUaXr1jV19HBieJoXGtKgkowKQXRGbPpJyCVGTixIXVfz2YWXYuBsWjyWqITp2Mu5naenZxedqWR57CVsBgEI8XaompWFC+5LJhd2Cdm58nxknsqsSEPl5UxrkKlCvJZ87qmY5aC8iGsvYCKw36HF5CLTCZMz9W+s3QQ0Q+MycgK0GRWRhh8hLI2E8N7D3j1foO66h45hKgHS0ixf1uc85ho2fHxRQGnsc83DbZNY61x9s7ODlddVGrlhHsQsnUI3yJKdswKU3Udqp//13sHuwY6ChGOV+bi7ks4513HHLqLD046PmxLk0u/B/nb1cqkNKMNNa+Pj0qnIfCYoflILG0CqCgmDMBNYAAPcskEWwiGVINj8Epvh5OtFNB71J8YmzhZALcvHoyFLbXAlpHCOC0hYGhoasYSLRQgRK4QuDVXRZb9eJCqyVVG67XUxhRmE8LDXPfCChKMoloXAkkcBPVeRpagvErlpqueWalCBjbo/xr22Nyk3F/UYcJNJGC4SPxNPcEmmYlGl+f75s9KkViLhpUlKw3G6dAj6OmccCDch/gqy0rCAYeFjOnVhU3q9wKbC8MlzG5JLgVG/Fj7jz0ujxFsR61yhzVP0tDFgIo9Z+XaqPz3diHo4FcCDuFPF/joLJlrh8VI/HxJLs57lZMinCSrRqqosnaF+Ymg1Xl4pi+QZXiPhdYiVoaxL3Kdzn8kxFh+N/Wxu6Gv7bLs0loUAEgOfxhpP1/29XJM2GcVAWKALJgjCXDrDE6LX3d2DeZtctjZ5jFcgS/FA90Gf4/61vgTFiFqG0a2k2i4hS4JOr9uHpH2JHsaZxOjwdEqylGBREQGRveFCsIi1dW33y39I8AJ48J8kcrmSJUtpo4DXSH/z0rjaebHb7eP0fvhqe/Dd6kK55XzqfOZ84fSdfWfgfOscOydO0AgaPzd+afza/K35e/OP5pvK9UZjhbnr1Frzz78BaGTZDg==</latexit><latexit sha1_base64="W7yxdQMaznTvXEOJTSOkBhZK5KA=">AAAIKHicnVXdbts2FJa7re60n6br5W7YxR6GTnbsdFmaFQEMpChWrMWy2WkLmEZGSUcWYeonJNXYIfQAu93eYk+zu6G3e48BO7Sc1XKyXYywJYrnfN9HnnNI+rngSvd6bxo33nn3vZvNW++7H3z40ce3t+588kJlhQzgJMhEJl/5TIHgKZxorgW8yiWwxBfw0p8dWfvL1yAVz9KRXuQwSdg05REPmMah062/PidUw1ybYzlGFgg0UfwCOq1ZiyjQpDVsTcghaV2czloloRR/7jWQypO06COKapo+apEgzngAlemoNSmXSHp2VrAQCWkkWWCQtcRHn3xJaBBmWmHn4tRQYUnIEaHSdsqysv4PWQ9tFdlwRYbas9VsXPd0a7vX7S0budrprzrbzqodn965eZeGWVAkkOpAMKXG/V6uJ4ZJzQMBpUsLBTkLZmwKY+ymLAE1Mcs8laSNIyGJMon/VJPlqLsOQR7JFjUWo5lfCCbn9VE/y2ZoUaXr1jV19HBieJoXGtKgkowKQXRGbPpJyCVGTixIXVfz2YWXYuBsWjyWqITp2Mu5naenZxedqWR57CVsBgEI8XaompWFC+5LJhd2Cdm58nxknsqsSEPl5UxrkKlCvJZ87qmY5aC8iGsvYCKw36HF5CLTCZMz9W+s3QQ0Q+MycgK0GRWRhh8hLI2E8N7D3j1foO66h45hKgHS0ixf1uc85ho2fHxRQGnsc83DbZNY61x9s7ODlddVGrlhHsQsnUI3yJKdswKU3Udqp//13sHuwY6ChGOV+bi7ks4513HHLqLD046PmxLk0u/B/nb1cqkNKMNNa+Pj0qnIfCYoflILG0CqCgmDMBNYAAPcskEWwiGVINj8Epvh5OtFNB71J8YmzhZALcvHoyFLbXAlpHCOC0hYGhoasYSLRQgRK4QuDVXRZb9eJCqyVVG67XUxhRmE8LDXPfCChKMoloXAkkcBPVeRpagvErlpqueWalCBjbo/xr22Nyk3F/UYcJNJGC4SPxNPcEmmYlGl+f75s9KkViLhpUlKw3G6dAj6OmccCDch/gqy0rCAYeFjOnVhU3q9wKbC8MlzG5JLgVG/Fj7jz0ujxFsR61yhzVP0tDFgIo9Z+XaqPz3diHo4FcCDuFPF/joLJlrh8VI/HxJLs57lZMinCSrRqqosnaF+Ymg1Xl4pi+QZXiPhdYiVoaxL3Kdzn8kxFh+N/Wxu6Gv7bLs0loUAEgOfxhpP1/29XJM2GcVAWKALJgjCXDrDE6LX3d2DeZtctjZ5jFcgS/FA90Gf4/61vgTFiFqG0a2k2i4hS4JOr9uHpH2JHsaZxOjwdEqylGBREQGRveFCsIi1dW33y39I8AJ48J8kcrmSJUtpo4DXSH/z0rjaebHb7eP0fvhqe/Dd6kK55XzqfOZ84fSdfWfgfOscOydO0AgaPzd+afza/K35e/OP5pvK9UZjhbnr1Frzz78BaGTZDg==</latexit><latexit sha1_base64="W7yxdQMaznTvXEOJTSOkBhZK5KA=">AAAIKHicnVXdbts2FJa7re60n6br5W7YxR6GTnbsdFmaFQEMpChWrMWy2WkLmEZGSUcWYeonJNXYIfQAu93eYk+zu6G3e48BO7Sc1XKyXYywJYrnfN9HnnNI+rngSvd6bxo33nn3vZvNW++7H3z40ce3t+588kJlhQzgJMhEJl/5TIHgKZxorgW8yiWwxBfw0p8dWfvL1yAVz9KRXuQwSdg05REPmMah062/PidUw1ybYzlGFgg0UfwCOq1ZiyjQpDVsTcghaV2czloloRR/7jWQypO06COKapo+apEgzngAlemoNSmXSHp2VrAQCWkkWWCQtcRHn3xJaBBmWmHn4tRQYUnIEaHSdsqysv4PWQ9tFdlwRYbas9VsXPd0a7vX7S0budrprzrbzqodn965eZeGWVAkkOpAMKXG/V6uJ4ZJzQMBpUsLBTkLZmwKY+ymLAE1Mcs8laSNIyGJMon/VJPlqLsOQR7JFjUWo5lfCCbn9VE/y2ZoUaXr1jV19HBieJoXGtKgkowKQXRGbPpJyCVGTixIXVfz2YWXYuBsWjyWqITp2Mu5naenZxedqWR57CVsBgEI8XaompWFC+5LJhd2Cdm58nxknsqsSEPl5UxrkKlCvJZ87qmY5aC8iGsvYCKw36HF5CLTCZMz9W+s3QQ0Q+MycgK0GRWRhh8hLI2E8N7D3j1foO66h45hKgHS0ixf1uc85ho2fHxRQGnsc83DbZNY61x9s7ODlddVGrlhHsQsnUI3yJKdswKU3Udqp//13sHuwY6ChGOV+bi7ks4513HHLqLD046PmxLk0u/B/nb1cqkNKMNNa+Pj0qnIfCYoflILG0CqCgmDMBNYAAPcskEWwiGVINj8Epvh5OtFNB71J8YmzhZALcvHoyFLbXAlpHCOC0hYGhoasYSLRQgRK4QuDVXRZb9eJCqyVVG67XUxhRmE8LDXPfCChKMoloXAkkcBPVeRpagvErlpqueWalCBjbo/xr22Nyk3F/UYcJNJGC4SPxNPcEmmYlGl+f75s9KkViLhpUlKw3G6dAj6OmccCDch/gqy0rCAYeFjOnVhU3q9wKbC8MlzG5JLgVG/Fj7jz0ujxFsR61yhzVP0tDFgIo9Z+XaqPz3diHo4FcCDuFPF/joLJlrh8VI/HxJLs57lZMinCSrRqqosnaF+Ymg1Xl4pi+QZXiPhdYiVoaxL3Kdzn8kxFh+N/Wxu6Gv7bLs0loUAEgOfxhpP1/29XJM2GcVAWKALJgjCXDrDE6LX3d2DeZtctjZ5jFcgS/FA90Gf4/61vgTFiFqG0a2k2i4hS4JOr9uHpH2JHsaZxOjwdEqylGBREQGRveFCsIi1dW33y39I8AJ48J8kcrmSJUtpo4DXSH/z0rjaebHb7eP0fvhqe/Dd6kK55XzqfOZ84fSdfWfgfOscOydO0AgaPzd+afza/K35e/OP5pvK9UZjhbnr1Frzz78BaGTZDg==</latexit>
Sparse model for fixed set size.

30. 30
How do we learn
model parameters from data?

31. We learn by maximum likelihood estimation.
31
• The good news.
Given the set of special sets H, finding the maximizer is “easy.”
• The bad news.
Finding the optimal set H is NP-hard (also not submodular).
[Benson-Kumar-Tomkins 18]
• The solution.
Heuristics for H, optimize the remaining parameters.
⟶ most frequent S, frequency normalized by frequency of items (lift),
lift normalized by set frequency
maximize
p,q,H, ,z
LL({Si, Ci}N
i=1 | p, q, H, , z)
subject to |H|  k<latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit>

32. We learn by maximum likelihood estimation.
32
maximize
p,q,H, ,z
LL({Si, Ci}N
i=1 | p, q, H, , z)
subject to |H|  k<latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit>
• Universal choice sets. Same alternatives available each time (Ci = C).
Groceries, department stores
• Theorem [Benson-Kumar-Tomkins 18]
Given H, the MLE has a closed form.
zj / number of size-j subsets<latexit sha1_base64="2855M5I5vXprMlJCH/vANmMlU8s=">AAAK4Xic3VZbb9xEFHbbUIq5tfQRHqbEK6Wt99Yq9IIiRRBVrdpCYdOLFIcwto/Xk50ZuzPjZjcj/wAekBCvvPAn+DH8G87YG7K7DfyAWlqvPXOu3/nmHMclZ9oMBn+fO39h7b2L71/6wP/wo48/+fTylc9e6KJSCTxPCl6oVzHVwJmE54YZDq9KBVTEHF7Gk2/d/ss3oDQr5K6ZlbAv6FiyjCXU4NLBlQt/HR8ckqhURWkKEhmYGisrEYMiRUY0O4ZucBgQXcUajK79TlAeWHZY/2R3arJFvmteSJ9EuhIHNkIhOwl5XbudCa8DYnIgIEqm0CUn6CemMePMzJz9yLKQHEY1iSK/s8GuN9LogQWEKnDSZaFcoKiK4bnd0+AME6AJMyBIgApME4QBEgOp32GSUDnDBUMCFxTDHGVhcPlhEBLWg17Y+DnNvIn/kNwnK+J1m2LwdRMjeZcuBzliHkRjKgTFam4MSXehkg6FBoJ5yXeuY6HJxrLACUxOxt0O6+uIFZXpO4oXAjZmb0AifYImzTl8SKvg9ZyFxpFVUJPkK/RP8UArFleO0o7Cc24GYYvUnJfzeiA9SzybN8nr9pBtkZM6BL2Dy+uD3qC5yNsPw/nD+na//PVPz/OeHVy5eDVKi6QSIE3CqdZ7w0Fp9i3F45VwqP2o0lDSZELHsIePkuLh2rdNg6lJB1dSkhUKf9KQZtVfVEE7is6WrFhD44pTNV1ejYtigjvYSvxlnya7u2+ZLCsDMmldZlV77LFvIXQKzzafkWW/hk2OQ8kSyBRNQio0wp6HJXNxhmZy3B0rWuahoBNIgPPTpTYqp85ZrKiauRSKIx3GaHmsikqmOiypMaCkRn2s2zTUOS1BhxkzIZYzce+p0yl5YQRVE/1fVnsCDMXNBjmOTXK3ygz8CGltFaTX7g6uxRz9Lkogc8YKQNa2+XMyRzl2uxWZmFdQW3dfkEA65caU+n6/jx29pw3ahmmSUzmGXlKI/usKtCOh7g+/2rx3615fg0BWqxjHgugeMZN3XRJdJrsxThNQjdztO+vtnx85QClOG4ePH405tnUe4Wvk1LZB6krBdlpwJMA2zpqkSGErUsDp9ES3wOCXSbS3O9y3rnCOAEtVfrY7otKBq0DCESYg8OTZKKOC8VkKGa24qbElZSfPyyTRmWMFDq9FZxorCOnWoHcvTARDp0gLjpRHB2aqM2diOUm0HUkzdaa2W2Wrb+zhWdvcr1eT2gE8ZApGMxEX/AGmZFsrurbfP31SW+lcCFZbUVuG4UYjMGcJ40K6qhLPVeY+nMIIxzMO/6avnO1g1cPowVMHyYmD3eESfDae1lbzUydOuNW2j1DSYUB5mdP6NNSfH62gno45sCTvttiftYOF1thelvuDcGYWqyxGbCzQU9SyypmzUSxs1K7Xb9FCPMHvn/QsjflGveziRjSNqdpD8kV5XExt9MbdO36Uq4oDyYGNc4Pd9c5maUiH7GJLp4mpsJ+jmh9NsEMMerc2YXo67jpkB1s9lQmQGMwRnl8n28wL3cDot646PiGNge6gNwTROdEe5fjdA5LJMcFJ4YYIh8zg91gKTmMhr/Vh/a8RHAC3/9eIajJprNQOBRwjw9Wh8fbDi1u9IYb3A86Tx157XfI+9770Nryhd8fb9h56z7znXrL2xdo3a4/XnviJ/4v/m/97K3r+3Fznqrd0+X/8A4P4bgk=</latexit><latexit sha1_base64="GECkuabdf1JANMsBaWDIa3dCdac=">AAAK4Xic3VbdbtxEFN62oRTz19JLuJgSr5S23r9WIU1RpBVEVau2UNj0R8qEMLaP15OdGbsz42Y3lh+ACyTELS/BDQ/D23DG3pDdbeABamm99sz5/c435zjMBTe23//7wsVLa+9dfv/KB96HH338yadXr332wmSFjuB5lIlMvwqZAcEVPLfcCniVa2AyFPAynHzr9l++AW14pvbsLIcDycaKJzxiFpcOr1366+TwiNBcZ7nNCLUwtaUqZAiaZAkx/AQ6/pFPTBEasKby2n5+WPKj6qdytyI75Lv6hfQINYU8LCkKlZNAVJXbmYjKJzYFAjLnGl0Kgn5CFnLB7czZpyUPyBGtCKVee4PfrKXRA/cJ0+Ck80y7QFEVw3O7Z8FZLsEQbkESHxW4IQgDRBZir80VYWqGC5b4LiiOOarM4vJDPyC8C92g9nOWeR3/EblPVsSrJkX/6zpG8i5dDnLE3KdjJiXDam4MSGehkg6FGoJ5yXdvYqHJxrLAKUxOxt2OqpuIFVPxO4oXAjbmb0Ahffw6zTl8SCv/9ZyF1pFVMhulK/SP8UBrHhaO0o7Cc276QYPUnJfzeiA9czybt8nr5pDtkNM6+N3Dq+v9br++yNsPg/nD+rCX//rny8fDZ4fXLl+ncRYVEpSNBDNmf9DP7UHJ8HhFAiqPFgZyFk3YGPbxUTE8XAdl3WAq0saVmCSZxp+ypF71FlXQjmazJSulZWEhmJ4ur4ZZNsEdbCXesk+b3DsoucoLCypqXCZFc+yxbyF0Gs+2mJFlv5ZPTgLFI0g0iwImDcKeBjl3cQZ2ctIZa5angWQTiECIs6UmKqcueKiZnrkUsmMThGh5rLNCxSbImbWglUF9rNs0MCnLwQQJtwGWM3LvsdPJRWYl0xPzX1a7EizDzRo5gU1yr0gs/AhxVWqIb9zr3wgF+l2UQOaMNYCqyvrPyRyn2O1WZEJRQFW6+4IE0im1Njf3ez3s6F1j0TZMo5SpMXSjTPZeF2AcCU1v8NXm9p3tngGJrNYhjgXZOeY27bgkOlx1QpwmoGu5u1vrzZ9HHaAMp43Dx6NjgW1dUHylTm0IyhQahnEmkABDnDVRFsMO1SDY9FQ3w+CXSbS/NzgoXeEcAZaq/GxvxJQDV4OCY0xA4skracIkF7MYElYIW2FLSk6fl0liEscKHF6LzgxWEOKdfnc7iCRHp0gLgZRHB3ZqEmdiOUm0TZWdOlPDRrk0t/bxrG0eVKtJ7QIeMg2jmQwz8QBTKhsrpiq/f/qkKpVzIXlVyqrkGC4dgT1PGBfiVZVwrjL34RRGOJ5x+Nd95XwHqx5GD546SE4d7A2W4CvDaVUacebECTfa5SOUdBgwkaesOgv150crqMdjATxKOw325+1goQ22l+X+IJ2ZxSrLER9L9EQbVjlzJQ1lSZv16i1ayCf4/ROfpzHfqJZd3KLTkOl9JB9Nw2xa0jfu3vZoqgsBJAU+Ti12163N3JI22cOWziJbYD9HNY9OsEP0u3c2YXo27tpkF1s9UxGQEOwxnl8nW88LU8PoNa7aHiG1gU6/OwDZPtUepfjdA4qrMcFJ4YaIgMTi91gMTmMhr/VB9a8RHAB3/9eIrjOprVQOBRwjg9Wh8fbDizvdAYb3A86Tx63mutL6vPVla6M1aG21hq2HrWet561o7Yu1b9Yerz3xIu8X7zfv90b04oW5zvXW0uX98Q/AOW77</latexit><latexit sha1_base64="GECkuabdf1JANMsBaWDIa3dCdac=">AAAK4Xic3VbdbtxEFN62oRTz19JLuJgSr5S23r9WIU1RpBVEVau2UNj0R8qEMLaP15OdGbsz42Y3lh+ACyTELS/BDQ/D23DG3pDdbeABamm99sz5/c435zjMBTe23//7wsVLa+9dfv/KB96HH338yadXr332wmSFjuB5lIlMvwqZAcEVPLfcCniVa2AyFPAynHzr9l++AW14pvbsLIcDycaKJzxiFpcOr1366+TwiNBcZ7nNCLUwtaUqZAiaZAkx/AQ6/pFPTBEasKby2n5+WPKj6qdytyI75Lv6hfQINYU8LCkKlZNAVJXbmYjKJzYFAjLnGl0Kgn5CFnLB7czZpyUPyBGtCKVee4PfrKXRA/cJ0+Ck80y7QFEVw3O7Z8FZLsEQbkESHxW4IQgDRBZir80VYWqGC5b4LiiOOarM4vJDPyC8C92g9nOWeR3/EblPVsSrJkX/6zpG8i5dDnLE3KdjJiXDam4MSGehkg6FGoJ5yXdvYqHJxrLAKUxOxt2OqpuIFVPxO4oXAjbmb0Ahffw6zTl8SCv/9ZyF1pFVMhulK/SP8UBrHhaO0o7Cc276QYPUnJfzeiA9czybt8nr5pDtkNM6+N3Dq+v9br++yNsPg/nD+rCX//rny8fDZ4fXLl+ncRYVEpSNBDNmf9DP7UHJ8HhFAiqPFgZyFk3YGPbxUTE8XAdl3WAq0saVmCSZxp+ypF71FlXQjmazJSulZWEhmJ4ur4ZZNsEdbCXesk+b3DsoucoLCypqXCZFc+yxbyF0Gs+2mJFlv5ZPTgLFI0g0iwImDcKeBjl3cQZ2ctIZa5angWQTiECIs6UmKqcueKiZnrkUsmMThGh5rLNCxSbImbWglUF9rNs0MCnLwQQJtwGWM3LvsdPJRWYl0xPzX1a7EizDzRo5gU1yr0gs/AhxVWqIb9zr3wgF+l2UQOaMNYCqyvrPyRyn2O1WZEJRQFW6+4IE0im1Njf3ez3s6F1j0TZMo5SpMXSjTPZeF2AcCU1v8NXm9p3tngGJrNYhjgXZOeY27bgkOlx1QpwmoGu5u1vrzZ9HHaAMp43Dx6NjgW1dUHylTm0IyhQahnEmkABDnDVRFsMO1SDY9FQ3w+CXSbS/NzgoXeEcAZaq/GxvxJQDV4OCY0xA4skracIkF7MYElYIW2FLSk6fl0liEscKHF6LzgxWEOKdfnc7iCRHp0gLgZRHB3ZqEmdiOUm0TZWdOlPDRrk0t/bxrG0eVKtJ7QIeMg2jmQwz8QBTKhsrpiq/f/qkKpVzIXlVyqrkGC4dgT1PGBfiVZVwrjL34RRGOJ5x+Nd95XwHqx5GD546SE4d7A2W4CvDaVUacebECTfa5SOUdBgwkaesOgv150crqMdjATxKOw325+1goQ22l+X+IJ2ZxSrLER9L9EQbVjlzJQ1lSZv16i1ayCf4/ROfpzHfqJZd3KLTkOl9JB9Nw2xa0jfu3vZoqgsBJAU+Ti12163N3JI22cOWziJbYD9HNY9OsEP0u3c2YXo27tpkF1s9UxGQEOwxnl8nW88LU8PoNa7aHiG1gU6/OwDZPtUepfjdA4qrMcFJ4YaIgMTi91gMTmMhr/VB9a8RHAB3/9eIrjOprVQOBRwjg9Wh8fbDizvdAYb3A86Tx63mutL6vPVla6M1aG21hq2HrWet561o7Yu1b9Yerz3xIu8X7zfv90b04oW5zvXW0uX98Q/AOW77</latexit><latexit sha1_base64="o0Mua147WDjqqenu5N2UDVjJE78=">AAAK4Xic3Vbrbts2FHbbrOu0W7v+3H6wiwyknezYLbJehgDBFhQt2m7dnF6AMMso6chiTFIqSTV2CD3A/g37u+fYw+xtdig5i+1me4AJsCyR5/qdj+coLgU3djD468LFS2vvXX7/ygfBhx99/MmnV6999tIUlU7gRVKIQr+OmQHBFbyw3Ap4XWpgMhbwKp585/dfvQVteKH27KyEA8nGimc8YRaXDq9d+vPk8IjQUhelLQi1MLVOVTIGTYqMGH4CvfAoJKaKDVhTB92wPHT8qP7Z7dZkm3zfvJBNQk0lDx1FITeJRF37nYmoQ2JzICBLrtGlIOgnZjEX3M68fep4RI5oTSgNuhv8ZiONHnhImAYvXRbaB4qqGJ7fPQvOcgmGcAuShKjADUEYILGQBl2uCFMzXLAk9EFxzFEVFpcfhRHhfehHjZ+zzJv4j8gDsiJetymG3zQxkv/T5SFHzEM6ZlIyrObGkPQWKulRaCCYl3z3JhaabCwLnMLkZfztqL6JWDGV/k/xQsDG/C0opE/YpDmHD2kVvpmz0HqySmaTfIX+KR5ozePKU9pTeM7NMGqRmvNyXg+kZ4ln8yvypj1k2+S0DmH/8Or6oD9oLvLuw3D+sN6ZX88Pr12+TtMiqSQomwhmzP5wUNoDx/B4JQLqgFYGSpZM2Bj28VExPFwHrmkwNeniSkqyQuNPWdKsBosqaEez2ZIVZ1lcCaany6txUUxwB1tJsOzTZvcOHFdlZUElrcusao899i2ETuPZFjOy7NfyyUmkeAKZZknEpEHY86jkPs7ITk56Y83KPJJsAgkIcbbURuXVBY810zOfQnFsohgtj3VRqdREJbMWtDKoj3WbRiZnJZgo4zbCcib+PfU6pSisZHpi/s1qX4JluNkgJ7BJ7lWZhZ8grZ2G9Ma9wY1YoN9FCWTOWAOo2jV/XuY4x263IhOLCmrn7wsSSKfc2tI82NzEjt43Fm3DNMmZGkM/KeTmmwqMJ6HZHH69df/2/U0DElmtYxwLsnfMbd7zSfS46sU4TUA3cnfurrd/AfWAMpw2Hp+AjgW2dUHxlXq1HVCm0rCTFgIJsIOzJilS2KYaBJue6hYY/DKJ9veGB84XzhNgqcrP90ZMeXA1KDjGBCSePEczJrmYpZCxStgaW1J2+rxMEpN5VuDwWnRmsIKQbg/696NEcnSKtBBIeXRgpybzJpaTRNtU2ak3tdMqO3NrH8/a1kG9mtQu4CHTMJrJuBAPMSXXWjG1++HZ09op70Ly2snacQyXjsCeJ4wL6apKPFeZ+/AKIxzPOPybvnK+g1UPo4fPPCSnDvaGS/C5eFo7I86ceOFW2z1GSY8BE2XO6rNQf3m8gno6FsCTvNdif94OFtpge1nuD9KbWayyHPGxRE+0ZZU352gsHW3X63doIZ/i9096nsZ8o152cYtOY6b3kXw0j4upo2/9vRvQXFcCSA58nFvsrne3Sku6ZA9bOktshf0c1QI6wQ4x6N/egunZuOuSXWz1TCVAYrDHeH69bDMvTANj0LrqBoQ0BnqD/hBk91R7lON3DyiuxgQnhR8iAjKL32MpeI2FvNaH9T9GcADc+U8jusmksVJ7FHCMDFeHxrsPL2/3hxjej4P1nSfzgXKl83nny85GZ9i529npPOo877zoJGtfrH279mTtaZAEvwa/Bb+3ohcvzHWud5au4I+/Afz0a/0=</latexit>
Let Nij = # times {i, j} selected and pD
ij = Nij/
P
{k,l} Nkl.
(i) pi /
P
j:{i,j} /2H Nij;
(ii) = (1
P
{i,j}2H pD
ij )/(
P
{k,l} /2H pkpl);
(iii) set q so that pipj + qij = pD
ij .<latexit sha1_base64="rg6rDbYXTGT5hVTWOS63WTy5VeY=">AAAIa3icfVXdbts2FLa7rc20v3a923bBLjaQdrJjp8jSdigWYEHRYu3W1UlbIMwySjqyGJOSQlKNU4Kvs6fZ7QbsIfYOO5TsxE6zCbBEk+f7vsPzQ0al4NoMBn+3r7z3/gdXr618GHz08Seffnb9xucvdVGpGPbiQhTqdcQ0CJ7DnuFGwOtSAZORgFfR5Ae//uoNKM2LfNeclnAg2TjnKY+ZwanDG+3vaV7wPIHckKdgSOenQ8uPHHlI6GqHGC5Bkw61PCRH1HUICkFsICEsT0inrG1/tTvefgZcJ1RX8tBSOwkFdc7PT4Tr9AmlwRq/7VGc0FIVpSlmtkfkAZlrEPTH8Jw8dg1h57sG6JF0zKRkqLU2JL0znTmuBs1c2rmNjpC1c1eIWKRGq4l/CXf7jB8FtA/AMe6yICZj5kwQPS4Pj8g35HgenLlMp394fXXQH9QPeXcwnA1WW7Pn+eGNqzdpUsSVxJDHgmm9PxyU5sAyZXgswAW00lCyeMLGsI/DnGEODmydake6OJOQtFD4w5TVs8EiBHkUO11isYZFlWBqujwbFcUEV7QLgmVNk947sDwvKwN53EimlSCYLl9BJOEKa0CckmVdwydvw5zHkCoWh0xqyUwWltz7GZrJ295YsTILJZtADEKcTzVeebjgkWLq1G+hONFhhMxjVVR5osOSGQMq14g3ik9DnbESdJhyE8ZMxP5/4jGlKIxkaqL/i7UvwTBcrCMnwNjdKjXwAhJnFSS37g1uRQJ1Fy1MBmMFkDtbf7zNScYNXLCJRAXO+veCRdAlmTGlfrC+bmDa1wa5YRpnLB9DPy7k+nEF2reiXh9+u3l/4/66BsmxYyNsUNk74Sbr+U30eN6LsK9B1XZ3t1abT0B9QBn2vY9PQMeiiJig+Jd62DbkulKwnRQCC2Abuz4uEnhIFQg2nWMLdH65iPZ3hwfWJ84XwFKWn++OWO6DqyCHE9yAxJPA0pRJLk4TSFkljLNUp/PxcpHo1FeFC7qLYhozCMnDQf9+GEuOolgWAkseBcxUp55ieZPITXMz9VTbDdjqO/vYa5sH7uKmdgCbTMHoVEaFeIRbsg2LdvbnZ0+dzb2E5M5KZzm6S0dgLjPGieQiJJpBZhoeMKoiTKepfEovF7ioMHr0zIdkLrA7XAqfjabOanEu4o0btH2Clj4GTJQZc+eu/vbkQtSTsQAeZ70m9petYKI1Hi/L54P0NItZliM+lqhEm6rydJZG0tJm3r1TFvIp3kTJZYjZgluWuEOnEVP7WHw0i4qppW/8uxvQTFUCSAZ8nBk8Xbc2S0O6ZDcDwmJTMUEQFtAJnhCD/sYmTLtk/nTJDt6iLI+BRGBOsH+9bX1/6TqMQSPVDQipCXqD/hBkd44eZYXC6PB8TIocrwUgAlJDNE/AIxb2tTp0ZyR4Adz9XxJV76RmcT4KeI0ML14a7w5ebvSH6N4vG6vbP84ulJXWl62vW2utYWurtd163Hre2mvF7d/bf7T/bP917Z+VmytfrHzVmF5pzzA3W0vPSvdf4ALtwA==</latexit><latexit sha1_base64="rg6rDbYXTGT5hVTWOS63WTy5VeY=">AAAIa3icfVXdbts2FLa7rc20v3a923bBLjaQdrJjp8jSdigWYEHRYu3W1UlbIMwySjqyGJOSQlKNU4Kvs6fZ7QbsIfYOO5TsxE6zCbBEk+f7vsPzQ0al4NoMBn+3r7z3/gdXr618GHz08Seffnb9xucvdVGpGPbiQhTqdcQ0CJ7DnuFGwOtSAZORgFfR5Ae//uoNKM2LfNeclnAg2TjnKY+ZwanDG+3vaV7wPIHckKdgSOenQ8uPHHlI6GqHGC5Bkw61PCRH1HUICkFsICEsT0inrG1/tTvefgZcJ1RX8tBSOwkFdc7PT4Tr9AmlwRq/7VGc0FIVpSlmtkfkAZlrEPTH8Jw8dg1h57sG6JF0zKRkqLU2JL0znTmuBs1c2rmNjpC1c1eIWKRGq4l/CXf7jB8FtA/AMe6yICZj5kwQPS4Pj8g35HgenLlMp394fXXQH9QPeXcwnA1WW7Pn+eGNqzdpUsSVxJDHgmm9PxyU5sAyZXgswAW00lCyeMLGsI/DnGEODmydake6OJOQtFD4w5TVs8EiBHkUO11isYZFlWBqujwbFcUEV7QLgmVNk947sDwvKwN53EimlSCYLl9BJOEKa0CckmVdwydvw5zHkCoWh0xqyUwWltz7GZrJ295YsTILJZtADEKcTzVeebjgkWLq1G+hONFhhMxjVVR5osOSGQMq14g3ik9DnbESdJhyE8ZMxP5/4jGlKIxkaqL/i7UvwTBcrCMnwNjdKjXwAhJnFSS37g1uRQJ1Fy1MBmMFkDtbf7zNScYNXLCJRAXO+veCRdAlmTGlfrC+bmDa1wa5YRpnLB9DPy7k+nEF2reiXh9+u3l/4/66BsmxYyNsUNk74Sbr+U30eN6LsK9B1XZ3t1abT0B9QBn2vY9PQMeiiJig+Jd62DbkulKwnRQCC2Abuz4uEnhIFQg2nWMLdH65iPZ3hwfWJ84XwFKWn++OWO6DqyCHE9yAxJPA0pRJLk4TSFkljLNUp/PxcpHo1FeFC7qLYhozCMnDQf9+GEuOolgWAkseBcxUp55ieZPITXMz9VTbDdjqO/vYa5sH7uKmdgCbTMHoVEaFeIRbsg2LdvbnZ0+dzb2E5M5KZzm6S0dgLjPGieQiJJpBZhoeMKoiTKepfEovF7ioMHr0zIdkLrA7XAqfjabOanEu4o0btH2Clj4GTJQZc+eu/vbkQtSTsQAeZ70m9petYKI1Hi/L54P0NItZliM+lqhEm6rydJZG0tJm3r1TFvIp3kTJZYjZgluWuEOnEVP7WHw0i4qppW/8uxvQTFUCSAZ8nBk8Xbc2S0O6ZDcDwmJTMUEQFtAJnhCD/sYmTLtk/nTJDt6iLI+BRGBOsH+9bX1/6TqMQSPVDQipCXqD/hBkd44eZYXC6PB8TIocrwUgAlJDNE/AIxb2tTp0ZyR4Adz9XxJV76RmcT4KeI0ML14a7w5ebvSH6N4vG6vbP84ulJXWl62vW2utYWurtd163Hre2mvF7d/bf7T/bP917Z+VmytfrHzVmF5pzzA3W0vPSvdf4ALtwA==</latexit><latexit sha1_base64="rg6rDbYXTGT5hVTWOS63WTy5VeY=">AAAIa3icfVXdbts2FLa7rc20v3a923bBLjaQdrJjp8jSdigWYEHRYu3W1UlbIMwySjqyGJOSQlKNU4Kvs6fZ7QbsIfYOO5TsxE6zCbBEk+f7vsPzQ0al4NoMBn+3r7z3/gdXr618GHz08Seffnb9xucvdVGpGPbiQhTqdcQ0CJ7DnuFGwOtSAZORgFfR5Ae//uoNKM2LfNeclnAg2TjnKY+ZwanDG+3vaV7wPIHckKdgSOenQ8uPHHlI6GqHGC5Bkw61PCRH1HUICkFsICEsT0inrG1/tTvefgZcJ1RX8tBSOwkFdc7PT4Tr9AmlwRq/7VGc0FIVpSlmtkfkAZlrEPTH8Jw8dg1h57sG6JF0zKRkqLU2JL0znTmuBs1c2rmNjpC1c1eIWKRGq4l/CXf7jB8FtA/AMe6yICZj5kwQPS4Pj8g35HgenLlMp394fXXQH9QPeXcwnA1WW7Pn+eGNqzdpUsSVxJDHgmm9PxyU5sAyZXgswAW00lCyeMLGsI/DnGEODmydake6OJOQtFD4w5TVs8EiBHkUO11isYZFlWBqujwbFcUEV7QLgmVNk947sDwvKwN53EimlSCYLl9BJOEKa0CckmVdwydvw5zHkCoWh0xqyUwWltz7GZrJ295YsTILJZtADEKcTzVeebjgkWLq1G+hONFhhMxjVVR5osOSGQMq14g3ik9DnbESdJhyE8ZMxP5/4jGlKIxkaqL/i7UvwTBcrCMnwNjdKjXwAhJnFSS37g1uRQJ1Fy1MBmMFkDtbf7zNScYNXLCJRAXO+veCRdAlmTGlfrC+bmDa1wa5YRpnLB9DPy7k+nEF2reiXh9+u3l/4/66BsmxYyNsUNk74Sbr+U30eN6LsK9B1XZ3t1abT0B9QBn2vY9PQMeiiJig+Jd62DbkulKwnRQCC2Abuz4uEnhIFQg2nWMLdH65iPZ3hwfWJ84XwFKWn++OWO6DqyCHE9yAxJPA0pRJLk4TSFkljLNUp/PxcpHo1FeFC7qLYhozCMnDQf9+GEuOolgWAkseBcxUp55ieZPITXMz9VTbDdjqO/vYa5sH7uKmdgCbTMHoVEaFeIRbsg2LdvbnZ0+dzb2E5M5KZzm6S0dgLjPGieQiJJpBZhoeMKoiTKepfEovF7ioMHr0zIdkLrA7XAqfjabOanEu4o0btH2Clj4GTJQZc+eu/vbkQtSTsQAeZ70m9petYKI1Hi/L54P0NItZliM+lqhEm6rydJZG0tJm3r1TFvIp3kTJZYjZgluWuEOnEVP7WHw0i4qppW/8uxvQTFUCSAZ8nBk8Xbc2S0O6ZDcDwmJTMUEQFtAJnhCD/sYmTLtk/nTJDt6iLI+BRGBOsH+9bX1/6TqMQSPVDQipCXqD/hBkd44eZYXC6PB8TIocrwUgAlJDNE/AIxb2tTp0ZyR4Adz9XxJV76RmcT4KeI0ML14a7w5ebvSH6N4vG6vbP84ulJXWl62vW2utYWurtd163Hre2mvF7d/bf7T/bP917Z+VmytfrHzVmF5pzzA3W0vPSvdf4ALtwA==</latexit><latexit sha1_base64="rg6rDbYXTGT5hVTWOS63WTy5VeY=">AAAIa3icfVXdbts2FLa7rc20v3a923bBLjaQdrJjp8jSdigWYEHRYu3W1UlbIMwySjqyGJOSQlKNU4Kvs6fZ7QbsIfYOO5TsxE6zCbBEk+f7vsPzQ0al4NoMBn+3r7z3/gdXr618GHz08Seffnb9xucvdVGpGPbiQhTqdcQ0CJ7DnuFGwOtSAZORgFfR5Ae//uoNKM2LfNeclnAg2TjnKY+ZwanDG+3vaV7wPIHckKdgSOenQ8uPHHlI6GqHGC5Bkw61PCRH1HUICkFsICEsT0inrG1/tTvefgZcJ1RX8tBSOwkFdc7PT4Tr9AmlwRq/7VGc0FIVpSlmtkfkAZlrEPTH8Jw8dg1h57sG6JF0zKRkqLU2JL0znTmuBs1c2rmNjpC1c1eIWKRGq4l/CXf7jB8FtA/AMe6yICZj5kwQPS4Pj8g35HgenLlMp394fXXQH9QPeXcwnA1WW7Pn+eGNqzdpUsSVxJDHgmm9PxyU5sAyZXgswAW00lCyeMLGsI/DnGEODmydake6OJOQtFD4w5TVs8EiBHkUO11isYZFlWBqujwbFcUEV7QLgmVNk947sDwvKwN53EimlSCYLl9BJOEKa0CckmVdwydvw5zHkCoWh0xqyUwWltz7GZrJ295YsTILJZtADEKcTzVeebjgkWLq1G+hONFhhMxjVVR5osOSGQMq14g3ik9DnbESdJhyE8ZMxP5/4jGlKIxkaqL/i7UvwTBcrCMnwNjdKjXwAhJnFSS37g1uRQJ1Fy1MBmMFkDtbf7zNScYNXLCJRAXO+veCRdAlmTGlfrC+bmDa1wa5YRpnLB9DPy7k+nEF2reiXh9+u3l/4/66BsmxYyNsUNk74Sbr+U30eN6LsK9B1XZ3t1abT0B9QBn2vY9PQMeiiJig+Jd62DbkulKwnRQCC2Abuz4uEnhIFQg2nWMLdH65iPZ3hwfWJ84XwFKWn++OWO6DqyCHE9yAxJPA0pRJLk4TSFkljLNUp/PxcpHo1FeFC7qLYhozCMnDQf9+GEuOolgWAkseBcxUp55ieZPITXMz9VTbDdjqO/vYa5sH7uKmdgCbTMHoVEaFeIRbsg2LdvbnZ0+dzb2E5M5KZzm6S0dgLjPGieQiJJpBZhoeMKoiTKepfEovF7ioMHr0zIdkLrA7XAqfjabOanEu4o0btH2Clj4GTJQZc+eu/vbkQtSTsQAeZ70m9petYKI1Hi/L54P0NItZliM+lqhEm6rydJZG0tJm3r1TFvIp3kTJZYjZgluWuEOnEVP7WHw0i4qppW/8uxvQTFUCSAZ8nBk8Xbc2S0O6ZDcDwmJTMUEQFtAJnhCD/sYmTLtk/nTJDt6iLI+BRGBOsH+9bX1/6TqMQSPVDQipCXqD/hBkd44eZYXC6PB8TIocrwUgAlJDNE/AIxb2tTp0ZyR4Adz9XxJV76RmcT4KeI0ML14a7w5ebvSH6N4vG6vbP84ulJXWl62vW2utYWurtd163Hre2mvF7d/bf7T/bP917Z+VmytfrHzVmF5pzzA3W0vPSvdf4ALtwA==</latexit>

33. A sparse model can lead to large likelihood gains.
33
Train model on 80% of data and evaluate likelihood on remaining 20%.

34. 34
Most positive q Most negative q
{indie, indie} 0.0301 {indie, metal} -0.0015
{rock, indie} 0.0174 {indie, progressive_metal} -0.0009
{hip_hop, hip_hop} 0.0123 {rock, rock, electronic} -0.0007
{indie, indie, indie} 0.0119 {indie, industrial} -0.0006
{rock, rock, rock} 0.0101 {metal, electronic} -0.0005
<latexit sha1_base64="rYpXM0JMurw2IlTRNfl9i1RVe0s=">AAAPXXic3Vdfb9s2EHe7tfO0rmnXhz3shV3qYShkx0qbphlQwMCKYsVarJvTP0AYZJR0lgiTokpSjVNB32OfZq/bV9jTvsqOkp1YTra9DEg7Apao4/373R2PdJgLbuxw+MeFix98eOnyR92PvU+ufHp17dr1z14YVegInkdKKP0qZAYEz+C55VbAq1wDk6GAl+H0W7f+8g1ow1W2a49y2JcsyfiER8wi6eB6N6AGUCpLbFpSy0JUaSCvyru5rcj7NzwaQsKzEpEUgumqFESQUUlTM+U5CYZSVkgQ7w00j1qV60LAeTvy3wzvqTKW5Mpwy98A+Yrcen0LnzU1g4QtUSk9b2f/fXhU8vh/lB1a8izm4JP6RStMxXAwvDMMcHK8JsEygWtI6+PqMNh6R3OFcLSKpido6lFDCrbvzj+OYeVaJRqMwQqkBwuMc4jDnXcAIsJJeU4PUpX7ZDFboJrD2rzTzBfImycIiKxWGY/oUuNbYNs+H2wrxbaSpQWgYGf+scxdGKt5U4MnMO6db4q8dsjdc7F/gvn+qYvqVDYW/r9buwjPUWWtkq65eRSy+PhE9Q6urdcO4yCnJ8F8st6Zj2cH1y/foLGKCgmZjQQzZi8Y5na/ZNrySEDl0QKvHCyasgT2cJoxCWa/rC83FekhJSYTpfGXWVJTvWUR1KPZUUvLwtlZmxoqNcUVU3le26ad3N/H+soLC1nUmJwUglhF3J2JxFxjysQRadu1fPrWxzTCRLPIZ9JIZlM/585P307f9hPN8tSXbAoRCHFCarxy4oKHmukjB0EdGj9EzYlWRRYbP2fWgs4MymO1z3yTshyMP+HWj5iI3HfsZHKhrGR6av5O68DVHS7WkRNgy91iYuEniKtSQ3zz/vBmKNDuModNAXshZFVZvxzPYcotrPCEooCqdM8lDq9HUmtz883GhoXZwFjUDbMoZVkCg0jJjdcFGHf5NBvBva2dzZ0NAxKbrg7x9Jf9Q27TvgPR51k/xJss6JrvzvZ688IzFwPK8M7q4uPRRKgQewF+Uic2gswUGkaxElgAI7znRiqGB1SDYLOFrELn20W0txvsly5xrgBaWX62O2aZC66GDA4RgGS4G+iESS6OYpiwQtiqpGaymLeLxExcVVReb9mYwQxC/GA42PEjydEoloXAkkcDdmYmTkUbJOqmmZ05VaNGuDS393Cvbe1Xq6AeAm4yDeMjGSrxCCGVjRZTlT88fVKVmTMheVXKquToLh2DPYsZCfGqSDgXmdtwAuMixHTawqX0bAOrFsaPnrqQLAzsBq3wleGsKo04MeKYG+nyMXK6GDCRp6w6cfXnxytRjxMBPEr7TezPWsFEG2wv7f4gnZrlLMsxTyRaok1VOXUlDWVJG3p1qizkE/zvFZ8lMV+o2iZu01nI9B4WH01DNSvpG/fseTStr5Up8CS12F23t3JLemQ3BcIiWzBBUMyjU+wQw8HmFsx6x627Rx7i/0aWRUBCsIe4fx0vQWPE1GH0GlM9j5BaAZ4/AcjeQnqcKo3R4VlCVEawqIiAiSWGx+AklnCtB9WxEndP/EclukZSa6lcFPAYCVYPjdOTF5uDAN37cXN99P38QOl2vuh82fm6E3S2O6POd51nneedqPtL99fub93fr/65dmntytrVhvXihbnMjU5rrH3+F2kI6yo=</latexit><latexit sha1_base64="rYpXM0JMurw2IlTRNfl9i1RVe0s=">AAAPXXic3Vdfb9s2EHe7tfO0rmnXhz3shV3qYShkx0qbphlQwMCKYsVarJvTP0AYZJR0lgiTokpSjVNB32OfZq/bV9jTvsqOkp1YTra9DEg7Apao4/373R2PdJgLbuxw+MeFix98eOnyR92PvU+ufHp17dr1z14YVegInkdKKP0qZAYEz+C55VbAq1wDk6GAl+H0W7f+8g1ow1W2a49y2JcsyfiER8wi6eB6N6AGUCpLbFpSy0JUaSCvyru5rcj7NzwaQsKzEpEUgumqFESQUUlTM+U5CYZSVkgQ7w00j1qV60LAeTvy3wzvqTKW5Mpwy98A+Yrcen0LnzU1g4QtUSk9b2f/fXhU8vh/lB1a8izm4JP6RStMxXAwvDMMcHK8JsEygWtI6+PqMNh6R3OFcLSKpido6lFDCrbvzj+OYeVaJRqMwQqkBwuMc4jDnXcAIsJJeU4PUpX7ZDFboJrD2rzTzBfImycIiKxWGY/oUuNbYNs+H2wrxbaSpQWgYGf+scxdGKt5U4MnMO6db4q8dsjdc7F/gvn+qYvqVDYW/r9buwjPUWWtkq65eRSy+PhE9Q6urdcO4yCnJ8F8st6Zj2cH1y/foLGKCgmZjQQzZi8Y5na/ZNrySEDl0QKvHCyasgT2cJoxCWa/rC83FekhJSYTpfGXWVJTvWUR1KPZUUvLwtlZmxoqNcUVU3le26ad3N/H+soLC1nUmJwUglhF3J2JxFxjysQRadu1fPrWxzTCRLPIZ9JIZlM/585P307f9hPN8tSXbAoRCHFCarxy4oKHmukjB0EdGj9EzYlWRRYbP2fWgs4MymO1z3yTshyMP+HWj5iI3HfsZHKhrGR6av5O68DVHS7WkRNgy91iYuEniKtSQ3zz/vBmKNDuModNAXshZFVZvxzPYcotrPCEooCqdM8lDq9HUmtz883GhoXZwFjUDbMoZVkCg0jJjdcFGHf5NBvBva2dzZ0NAxKbrg7x9Jf9Q27TvgPR51k/xJss6JrvzvZ688IzFwPK8M7q4uPRRKgQewF+Uic2gswUGkaxElgAI7znRiqGB1SDYLOFrELn20W0txvsly5xrgBaWX62O2aZC66GDA4RgGS4G+iESS6OYpiwQtiqpGaymLeLxExcVVReb9mYwQxC/GA42PEjydEoloXAkkcDdmYmTkUbJOqmmZ05VaNGuDS393Cvbe1Xq6AeAm4yDeMjGSrxCCGVjRZTlT88fVKVmTMheVXKquToLh2DPYsZCfGqSDgXmdtwAuMixHTawqX0bAOrFsaPnrqQLAzsBq3wleGsKo04MeKYG+nyMXK6GDCRp6w6cfXnxytRjxMBPEr7TezPWsFEG2wv7f4gnZrlLMsxTyRaok1VOXUlDWVJG3p1qizkE/zvFZ8lMV+o2iZu01nI9B4WH01DNSvpG/fseTStr5Up8CS12F23t3JLemQ3BcIiWzBBUMyjU+wQw8HmFsx6x627Rx7i/0aWRUBCsIe4fx0vQWPE1GH0GlM9j5BaAZ4/AcjeQnqcKo3R4VlCVEawqIiAiSWGx+AklnCtB9WxEndP/EclukZSa6lcFPAYCVYPjdOTF5uDAN37cXN99P38QOl2vuh82fm6E3S2O6POd51nneedqPtL99fub93fr/65dmntytrVhvXihbnMjU5rrH3+F2kI6yo=</latexit><latexit sha1_base64="rYpXM0JMurw2IlTRNfl9i1RVe0s=">AAAPXXic3Vdfb9s2EHe7tfO0rmnXhz3shV3qYShkx0qbphlQwMCKYsVarJvTP0AYZJR0lgiTokpSjVNB32OfZq/bV9jTvsqOkp1YTra9DEg7Apao4/373R2PdJgLbuxw+MeFix98eOnyR92PvU+ufHp17dr1z14YVegInkdKKP0qZAYEz+C55VbAq1wDk6GAl+H0W7f+8g1ow1W2a49y2JcsyfiER8wi6eB6N6AGUCpLbFpSy0JUaSCvyru5rcj7NzwaQsKzEpEUgumqFESQUUlTM+U5CYZSVkgQ7w00j1qV60LAeTvy3wzvqTKW5Mpwy98A+Yrcen0LnzU1g4QtUSk9b2f/fXhU8vh/lB1a8izm4JP6RStMxXAwvDMMcHK8JsEygWtI6+PqMNh6R3OFcLSKpido6lFDCrbvzj+OYeVaJRqMwQqkBwuMc4jDnXcAIsJJeU4PUpX7ZDFboJrD2rzTzBfImycIiKxWGY/oUuNbYNs+H2wrxbaSpQWgYGf+scxdGKt5U4MnMO6db4q8dsjdc7F/gvn+qYvqVDYW/r9buwjPUWWtkq65eRSy+PhE9Q6urdcO4yCnJ8F8st6Zj2cH1y/foLGKCgmZjQQzZi8Y5na/ZNrySEDl0QKvHCyasgT2cJoxCWa/rC83FekhJSYTpfGXWVJTvWUR1KPZUUvLwtlZmxoqNcUVU3le26ad3N/H+soLC1nUmJwUglhF3J2JxFxjysQRadu1fPrWxzTCRLPIZ9JIZlM/585P307f9hPN8tSXbAoRCHFCarxy4oKHmukjB0EdGj9EzYlWRRYbP2fWgs4MymO1z3yTshyMP+HWj5iI3HfsZHKhrGR6av5O68DVHS7WkRNgy91iYuEniKtSQ3zz/vBmKNDuModNAXshZFVZvxzPYcotrPCEooCqdM8lDq9HUmtz883GhoXZwFjUDbMoZVkCg0jJjdcFGHf5NBvBva2dzZ0NAxKbrg7x9Jf9Q27TvgPR51k/xJss6JrvzvZ688IzFwPK8M7q4uPRRKgQewF+Uic2gswUGkaxElgAI7znRiqGB1SDYLOFrELn20W0txvsly5xrgBaWX62O2aZC66GDA4RgGS4G+iESS6OYpiwQtiqpGaymLeLxExcVVReb9mYwQxC/GA42PEjydEoloXAkkcDdmYmTkUbJOqmmZ05VaNGuDS393Cvbe1Xq6AeAm4yDeMjGSrxCCGVjRZTlT88fVKVmTMheVXKquToLh2DPYsZCfGqSDgXmdtwAuMixHTawqX0bAOrFsaPnrqQLAzsBq3wleGsKo04MeKYG+nyMXK6GDCRp6w6cfXnxytRjxMBPEr7TezPWsFEG2wv7f4gnZrlLMsxTyRaok1VOXUlDWVJG3p1qizkE/zvFZ8lMV+o2iZu01nI9B4WH01DNSvpG/fseTStr5Up8CS12F23t3JLemQ3BcIiWzBBUMyjU+wQw8HmFsx6x627Rx7i/0aWRUBCsIe4fx0vQWPE1GH0GlM9j5BaAZ4/AcjeQnqcKo3R4VlCVEawqIiAiSWGx+AklnCtB9WxEndP/EclukZSa6lcFPAYCVYPjdOTF5uDAN37cXN99P38QOl2vuh82fm6E3S2O6POd51nneedqPtL99fub93fr/65dmntytrVhvXihbnMjU5rrH3+F2kI6yo=</latexit><latexit sha1_base64="rYpXM0JMurw2IlTRNfl9i1RVe0s=">AAAPXXic3Vdfb9s2EHe7tfO0rmnXhz3shV3qYShkx0qbphlQwMCKYsVarJvTP0AYZJR0lgiTokpSjVNB32OfZq/bV9jTvsqOkp1YTra9DEg7Apao4/373R2PdJgLbuxw+MeFix98eOnyR92PvU+ufHp17dr1z14YVegInkdKKP0qZAYEz+C55VbAq1wDk6GAl+H0W7f+8g1ow1W2a49y2JcsyfiER8wi6eB6N6AGUCpLbFpSy0JUaSCvyru5rcj7NzwaQsKzEpEUgumqFESQUUlTM+U5CYZSVkgQ7w00j1qV60LAeTvy3wzvqTKW5Mpwy98A+Yrcen0LnzU1g4QtUSk9b2f/fXhU8vh/lB1a8izm4JP6RStMxXAwvDMMcHK8JsEygWtI6+PqMNh6R3OFcLSKpido6lFDCrbvzj+OYeVaJRqMwQqkBwuMc4jDnXcAIsJJeU4PUpX7ZDFboJrD2rzTzBfImycIiKxWGY/oUuNbYNs+H2wrxbaSpQWgYGf+scxdGKt5U4MnMO6db4q8dsjdc7F/gvn+qYvqVDYW/r9buwjPUWWtkq65eRSy+PhE9Q6urdcO4yCnJ8F8st6Zj2cH1y/foLGKCgmZjQQzZi8Y5na/ZNrySEDl0QKvHCyasgT2cJoxCWa/rC83FekhJSYTpfGXWVJTvWUR1KPZUUvLwtlZmxoqNcUVU3le26ad3N/H+soLC1nUmJwUglhF3J2JxFxjysQRadu1fPrWxzTCRLPIZ9JIZlM/585P307f9hPN8tSXbAoRCHFCarxy4oKHmukjB0EdGj9EzYlWRRYbP2fWgs4MymO1z3yTshyMP+HWj5iI3HfsZHKhrGR6av5O68DVHS7WkRNgy91iYuEniKtSQ3zz/vBmKNDuModNAXshZFVZvxzPYcotrPCEooCqdM8lDq9HUmtz883GhoXZwFjUDbMoZVkCg0jJjdcFGHf5NBvBva2dzZ0NAxKbrg7x9Jf9Q27TvgPR51k/xJss6JrvzvZ688IzFwPK8M7q4uPRRKgQewF+Uic2gswUGkaxElgAI7znRiqGB1SDYLOFrELn20W0txvsly5xrgBaWX62O2aZC66GDA4RgGS4G+iESS6OYpiwQtiqpGaymLeLxExcVVReb9mYwQxC/GA42PEjydEoloXAkkcDdmYmTkUbJOqmmZ05VaNGuDS393Cvbe1Xq6AeAm4yDeMjGSrxCCGVjRZTlT88fVKVmTMheVXKquToLh2DPYsZCfGqSDgXmdtwAuMixHTawqX0bAOrFsaPnrqQLAzsBq3wleGsKo04MeKYG+nyMXK6GDCRp6w6cfXnxytRjxMBPEr7TezPWsFEG2wv7f4gnZrlLMsxTyRaok1VOXUlDWVJG3p1qizkE/zvFZ8lMV+o2iZu01nI9B4WH01DNSvpG/fseTStr5Up8CS12F23t3JLemQ3BcIiWzBBUMyjU+wQw8HmFsx6x627Rx7i/0aWRUBCsIe4fx0vQWPE1GH0GlM9j5BaAZ4/AcjeQnqcKo3R4VlCVEawqIiAiSWGx+AklnCtB9WxEndP/EclukZSa6lcFPAYCVYPjdOTF5uDAN37cXN99P38QOl2vuh82fm6E3S2O6POd51nneedqPtL99fub93fr/65dmntytrVhvXihbnMjU5rrH3+F2kI6yo=</latexit>

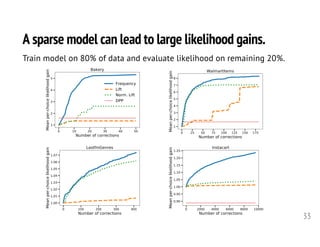
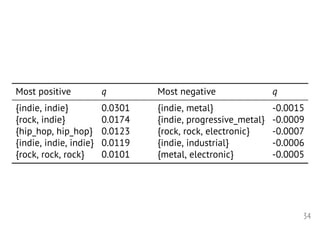
35. We learn by maximum likelihood estimation.
35
maximize
p,q,H, ,z
LL({Si, Ci}N
i=1 | p, q, H, , z)
subject to |H|  k<latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit><latexit sha1_base64="707x0S5/YqBTy1rPPzphETN+EXg=">AAAIEHicfVXdbts2FHa6rem0v3a93A27wEUXyI6dImuzIkCAFkWKpls2J22BMMso6UjiTFIKSTVOCL7EnmZ3w273BnuAvccOZaeJk2wyLNOH53wfzzkfyaQW3NjB4O+FGx98+NHNxVsfR598+tnnX9y+8+VrUzU6hb20EpV+mzADgivYs9wKeFtrYDIR8CYZPw3zb96BNrxSu/akhgPJCsVznjKLpsPb/9AECq4cHDWtZdnPDEzwQkHmo/uENipDCLCujslRTLZiQgsmJYvJqXfUwsQ6ySZc8lPwntzHD5lat7f9A+pGhzwmTw859YeObwz9z+57T+gTiuuy9Am5CvoNoTTwthimSX6F1BJbnUGLEEi2CNXtgAog44iCyt4vuv1znlJ0eHtp0B+0D7k6GM4GS53Zs3N45+ZdmlVpI0HZVDBj9oeD2h44pi1PBfiINgZqlo5ZAfs4VEyCOXBtPzzpoiUjeaXxqyxprdHFEMTR7GQOxVmWNILpybw1qaoxzhgfRfOcNn984LiqGwsqnVLmjcAqkdBmknGNRRMnZJ7X8vFprHgKuWZpzKSRzJZxzcM6Yzs+7RWa1WUs2RhSEOLcNF1VCBc80UyfhBSqYxMniFzoCiVi4ppZC1oZjLeaT2JTshpMnHMbp0yk4X8WYmpRWcn02PwXal+CZTjZVk6g8Hab3MJP2FmnIbv3eHAvEch70cOWUGgA5V37E3yOS27hkk8iGvAuvC94RF1SWlub71ZWUHJ9YxEbJmnJVAH9tJIrRw2YICWzMvx2bX11fcWA5Ci+BAUme8fclr2QRI+rXoKbD3Tr9/DR0vQnoqGgDDdnqE9EC1ElTKBuLQ1hm6BMo2EzqwQKYBO3ZlplsEE1CDY5i61w8fMi2t8dHrjQuCCAuS7v7I6YCsXVoOAYE5AM9wPNmeTiJIOcNcLixjX52XheJCYPqvBR9yKZwQ5CtjHor8ep5EiKshAoeSSwE5MHiPkkEZsqOwlQm9NgZ5b3ca+tHfjLST0D3GQaRicyqcRzTMlNUYx3P7za9k4FCsm9k95xXC4dgb3OGQ3Z5ZBkFjLjCAGjJsF22ia09HqCywyj569CSc4Idodz5XPJxDsjzkmC8zTavUDPUAMm6pL586X+8uJS1bNCAE/L3rT2181gow0eL/PngwwwF7ssR7yQyESnqgpwjibS0andX5GF3MbrIrsuYjbh5ymW6SRheh/FR8ukmjj6Lry7ES11g0dxCbwoLZ6uj9ZqS7pktwTCUtswQTAsomM8IQb91TWYdMnZ0yXP8KpjKgWSgD3G/Rt8CZIR05YxmlJ1Izz+A0Bv0B+C7J5Fj8pKY3W4KkilCIqKCMgtMTyDEHEhr6Whfw+CF8DD/wXRbSYtig9VwGtkePnSuDp4vdof4vJ+XF3afDm7UG51vup83XnQGXYedTY7W52dzl4nXXi5cLRwuuAWf1v8ffGPxT+nrjcWZjF3O3PP4l//AlS51bk=</latexit>
• Variable choice sets. Availability changes (Ci varies).
Subset of clicked-on items on Amazon that you buy in browsing session.
• Theorem [Benson-Kumar-Tomkins 18]
Given H, the objective can be transformed into a concave function
with some linear constraints.

36. 36
0 5 10 15 20
Number of corrections
1.00
1.01
1.02
1.03
1.04
1.05
1.06
1.07
1.08
Meanper-choicelikelihoodgain
YcCats
YcItems
A sparse model can lead to large likelihood gains.
Data from 2015 RecSys challenge (http://2015.recsyschallenge.com/)
Train model on 80% of data and evaluate likelihood on remaining 20%.

37. 37
Recap on Set Prediction #2.
Discrete subset choice models.
1. Discrete choice theory is a staple in behavioral econ and ML,
but typically only accounts for single-item structure.
2. Our discrete subset choice model uses linearly separable
utilities with “sparse corrections.”
3. In real-world datasets, a few corrections can lead to a
substantial gain in likelihood.
Code. bit.ly/subset-choice-code
Data. bit.ly/subset-choice-data

38. 38
Set Prediction #3. Higher-order link prediction.
Given a time-evolving hypergraph, which new hyperedges appear?
Which new teams form? Which new substances are combined in drug design?
Simplicial closure and higher-order link prediction.
Benson, Abebe, Schaub, Jadbabaie, & Kleinberg. arXiv:1802.0619, 2018.

39. Networks are sets of nodes and edges (graphs) that
model real-world systems.
39
Collaboration
nodes are people/groups
edges link entities
working together
Communications
nodes are people/accounts
edges show info. exchange
Physical proximity
nodes are people/animals
edges link those that interact
in close proximity
Drug compounds
nodes are substances
edge between substances that
appear in the same drug

40. Real-world systems are composed of“higher-order”
interactions that we often reduce to pairwise ones.
40
Collaboration
nodes are people/groups
teams are made up of
small groups
Communications
nodes are people/accounts
emails often have several
recipients,not just one
Physical proximity
nodes are people/animals
people often gather in
small groups
Drug compounds
nodes are substances
drugs are made up of
several substances

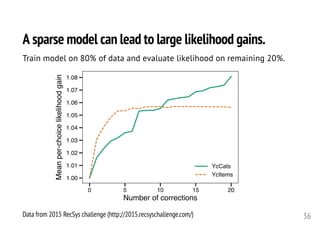
41. There are many ways to mathematically represent the
higher-order structure present in relational data.
41
• Hypergraphs [Berge 89]
• Set systems [Frankl 95]
• Tensors [Kolda-Bader 09]
• Affiliation networks [Feld 81,Newman-Watts-Strogatz 02]
• Multipartite networks [Lambiotte-Ausloos 05,Lind-Herrmann 07]
• Abstract simplicial complexes [Lim 15,Osting-Palande-Wang 17]
• Multilayer networks [Kivelä+ 14,Boccaletti+ 14,many others…]
• Meta-paths [Sun-Han 12]
• Motif-based representations [Benson-Gleich-Leskovec 15,17]
• …
Data representation is not the problem.
The problem is how do we evaluate and compare models and algorithms?

42. Link prediction is a classical machine learning problem
in network science that is used to evaluate models.
42
We observe data which is a list of edges in a graph up to some point t.
We want to predict which new edges will form in the future.
Shows up in a variety of applications
• Predicting new social relationships and friend recommendation.
[Backstrom-Leskovec 11; Wang+ 15]
• Inferring new links between genes and diseases.
[Wang-Gulbahce-Yu 11; Moreau-Tranchevent 12]
• Suggesting novel connections in the scientific community.
[Liben-Nowell-Kleinberg 07; Tang-Wu-Sun-Su 12]
Link prediction is also used as a framework to compare models/algorithms.
[Liben-Nowell-Kleinberg 03, 07; Lü-Zhau 11]

43. We propose“higher-order link prediction”as a similar
framework for evaluation of higher-order models.
43
t1 : {1, 2, 3, 4}
t2 : {1, 3, 5}
t3 : {1, 6}
t4 : {2, 6}
t5 : {1, 7, 8}
t6 : {3, 9}
t7 : {5, 8}
t8 : {1, 2, 6}
Data.
Observe simplices up to some
time t. Using this data, want to
predict what groups of > 2
nodes will appear in a simplex
in the future.
t
1
2
3
4
5
6
7
8
9
We predict structure that classical link
prediction would not even consider!
Possible applications
• Novel combinations of drugs for treatments.
• Group chat recommendation in social networks.
• Team formation.

44. Thinking of higher-order data as a weighted projected
graph with“filled-in”structures is a convenient viewpoint.
44
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
2
2
1
1
1
1
1
1
1
1
1
1
1
1
1
t1 : {1, 2, 3, 4}
t2 : {1, 3, 5}
t3 : {1, 6}
t4 : {2, 6}
t5 : {1, 7, 8}
t6 : {3, 9}
t7 : {5, 8}
t8 : {1, 2, 6}
Data. Pictures to have in mind.
Projected graph W.
Wij = # of simplices containing nodes i and j.

45. 45
5
23
16
20

46. 46
i
j k
i
j k
Warm-up. What’s more common in data?
or
“Open triangle”
each pair has been in a simplex
together but all 3 nodes have
never been in the same simplex
“Closed triangle”
there is some simplex that
contains all 3 nodes

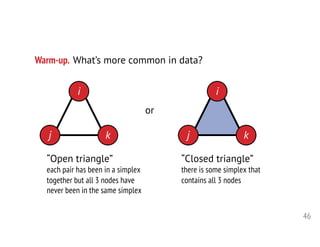
47. music-rap-genius
NDC-substances
NDC-classes
DAWN
coauth-DBLP
coauth-MAG-geology
coauth-MAG-history
congress-bills
congress-committees
tags-stack-overflow
tags-math-sx
tags-ask-ubuntu
email-Eu
email-Enron
threads-stack-overflow
threads-math-sx
threads-ask-ubuntu
contact-high-school
contact-primary-school
10 5
10 4
10 3
10 2
10 1
Edge density in projected graph
0.00
0.25
0.50
0.75
1.00
Fractionoftrianglesopen
There is lots of variation in the fraction of triangles that
are open,but datasets from the same domain are similar.
47
See also [Patania-Petri-Vaccarino 17] for fraction of open
triangles on several arxiv collaboration networks.

48. A simple model can account for open triangle variation.
48
• n nodes; only 3-node simplices; {i, j, k} included with prob. p = 1 / nb i.i.d.
• ⟶ always get ϴ(pn3) = ϴ(n3 - b) closed triangles in expectation.
b = 0.8, 0.82, 0.84, ..., 1.8
Larger b is darker marker.
Proposition (sketch).
• b < 1 ⟶ ϴ(n3) open triangles in
expectation for large n.
• b > 1 ⟶ ϴ(n3(2-b)) open triangles
in expectation for large n.
• The number of open triangles
grows faster for b < 3/2.
10 1
100
Edge density in projected graph
0.00
0.25
0.50
0.75
1.00
Fractionoftrianglesopen
Exactly 3 nodes per simplex (simulated)
n = 200
n = 100
n = 50
n = 25

49. Dataset domain separation also occurs at the local level.
49
• Randomly sample 100 egonets per dataset and measure
log of average degree and fraction of open triangles.
• Logistic regression model to predict domain
(coauthorship, tags, threads, email, contact).
• 75% model accuracy vs. 21% with random guessing.

50. 50
Simplicial closure.
How do new simplices appear?
How do new closed triangles appear?

51. Groups of nodes go through trajectories until finally
reaching a“simplicial closure event.”
51
1
2
3
4
5
6
7
8
9
t1 : {1, 2, 3, 4}
t2 : {1, 3, 5}
t3 : {1, 6}
t4 : {2, 6}
t5 : {1, 7, 8}
t6 : {3, 9}
t7 : {5, 8}
t8 : {1, 2, 6}
1
2 6
1
2 6
1
2 6
1
2 6
1
2 6
{1, 2, 3, 4}
t1
{1, 6}
t3
{2, 6}
t4
{1, 2, 6}
t8
For this talk, we will focus on simplicial closure on 3 nodes.

52. Groups of nodes go through trajectories until finally
reaching a“simplicial closure event.”
52
Substances in marketed drugs recorded in the National Drug Code directory.
HIV protease
inhibitors
UGT1A1
inhibitors
Breast cancer
resistance protein inhibitors
1
2+
2+
1
2+
1
1
2+
2+
1
2+
2+
2+
Reyataz
RedPharm
2003
Reyataz
Squibb & Sons
2003
Kaletra
Physicians
Total Care
2006
Promacta
GSK (25mg)
2008
Promacta
GSK (50mg)
2008
Kaletra
DOH Central
Pharmacy
2009
Evotaz
Squibb & Sons
2015
We bin weighted edges into “weak” and “strong ties” in the projected graph W.
Wij = # of simplices containing nodes i and j.
• Weak ties. Wij = 1 (one simplex contains i and j)
• Strong ties. Wij > 2 (at least two simplices contain i and j)

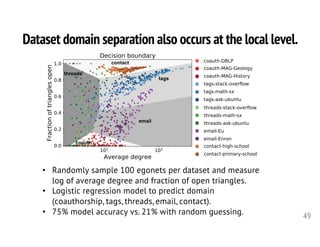
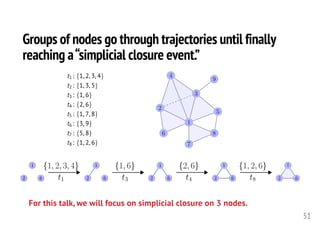
53. Simplicial closure depends on structure in projected graph.
53
• First 80% of the data (in time) ⟶ record configurations of triplets not in closed triangle.
• Remainder of data ⟶ find fraction that are now closed triangles.
Increased edge density
increases closure probability.
Increased tie strength
increases closure probability.
Tension between edge
density and tie strength.
Left and middle observations are consistent with theory and empirical studies of social networks.
[Granovetter 73; Leskovec+ 08; Backstrom+ 06; Kossinets-Watts 06]
Closure probability Closure probability Closure probability

54. 54
How do we use these principles to
do higher-order link prediction?

55. 55
Our structural analysis tells us what we should be
looking at for prediction.
1. Edge density is a positive indicator.
⟶ focus our attention on predicting which open
triangles become closed triangles.
2. Tie strength is a positive indicator.
⟶ various ways of incorporating this information
i
j k
Wij
Wjk
Wjk

56. 56
For every open triangle,we assign a score function on
first 80% of data based on structural properties.
Four broad classes of score functions for an open triangle.
Score s(i, j, k)…
1. is a function of Wij, Wjk, Wjk
arithmetic mean, geometric mean, etc.
2. looks at common neighbors of the three nodes.
generalized Jaccard, Adamic-Adar, etc.
3. uses “whole-network” similarity scores on projected graph
sum of PageRank or Katz scores amongst edges
4. is learned from data
train a logistic regression model with features
i
j k
Wij
Wjk
Wjk
After computing scores, predict that open triangles with highest
scores will be closed triangles in final 20% of data.

57. 57

58. 58
A few lessons learned from applying all of these ideas.
1. We can predict pretty well on all datasets using some method.
→ 4x to 107x better than random w/r/t mean average precision
depending on the dataset/method
2. Thread co-participation and co-tagging on stack exchange are
consistently easy to predict.
3. Simply averaging Wij, Wjk, and Wik consistently performs well.
i
j k
Wij
Wjk
Wjk

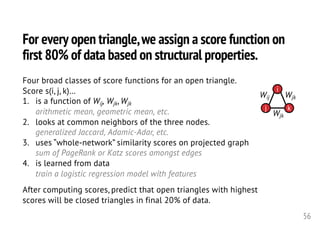
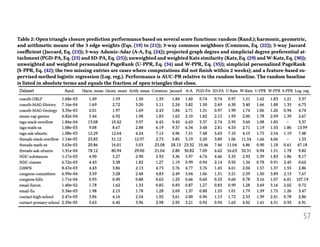
59. Generalized means of edges weights are often good
predictors of new 3-node simplices appearing.
59
music-rap-genius
NDC-substances
NDC-classes
DAWN
coauth-DBLP
coauth-MAG-geology
coauth-MAG-history
congress-bills
congress-committees
tags-stack-overflow
tags-math-sx
tags-ask-ubuntu
email-Eu
email-Enron
threads-stack-overflow
threads-math-sx
threads-ask-ubuntu
contact-high-school
contact-primary-school
harmonic geometric arithmetic
p
4 3 2 1 0 1 2 3 4
0
20
40
60
80
Relativeperformance
4 3 2 1 0 1 2 3 4
p
2.5
5.0
7.5
10.0
12.5
Relativeperformance
4 3 2 1 0 1 2 3 4
p
1.0
1.5
2.0
2.5
3.0
3.5
Relativeperformance
Good performance from this local information is a deviation from classical link prediction, where
methods that use long paths (e.g., PageRank) perform well [Liben-Nowell & Kleinberg 07].
For structures on k nodes, the subsets of size k-1 contain rich information only when k > 2.
i
j k
Wij
Wjk
Wjk
i
j k
?
scorep(i, j, k)
= (Wp
ij + Wp
jk + Wp
ik)1/p
<latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit><latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit><latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit><latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit>

60. 60
Recap on Set Prediction #3.
Higher-order link prediction.
1. Higher-order data is pervasive!
We have ways to represent data, and higher-order link prediction is a
general framework for comparing comparing models and methods.
2. There is rich static and temporal structure in the datasets we collected.
3. Do you have a better model, algorithm, or data representation?
Great! Let’ s out-perform these baselines.
Code. bit.ly/sc-holp-code
Data. bit.ly/sc-holp-data

61. 61
THANKS!
Slides. bit.ly/arb-SCAN18
Austin R. Benson
http://cs.cornell.edu/~arb
@austinbenson
arb@cs.cornell.edu
Set prediction three ways
1. Repeat sets at the
individual level
2. Repeat and novel sets at the
group level
3. Novel sets at the
complex systems level

62. Most open triangles do not come from asynchronous
temporal behavior.
62
i
j k
In 61.1% to 97.4% of open triangles,
all three pairs of edges have an
overlapping period of activity.
⟶ there is an overlapping period of
activity between all 3 edges
(Helly’s theorem).
# overlaps
Dataset # open triangles 0 1 2 3
coauth-DBLP 1,295,214 0.012 0.143 0.123 0.722
coauth-MAG-history 96,420 0.002 0.055 0.059 0.884
coauth-MAG-geology 2,494,960 0.010 0.128 0.109 0.753
tags-stack-overflow 300,646,440 0.002 0.067 0.071 0.860
tags-math-sx 2,666,353 0.001 0.040 0.049 0.910
tags-ask-ubuntu 3,288,058 0.002 0.088 0.085 0.825
threads-stack-overflow 99,027,304 0.001 0.034 0.037 0.929
threads-math-sx 11,294,665 0.001 0.038 0.039 0.922
threads-ask-ubuntu 136,374 0.000 0.020 0.023 0.957
NDC-substances 1,136,357 0.020 0.196 0.151 0.633
NDC-classes 9,064 0.022 0.191 0.136 0.652
DAWN 5,682,552 0.027 0.216 0.155 0.602
congress-committees 190,054 0.001 0.046 0.058 0.895
congress-bills 44,857,465 0.003 0.063 0.113 0.821
email-Enron 3,317 0.008 0.130 0.151 0.711
email-Eu 234,600 0.010 0.131 0.132 0.727
contact-high-school 31,850 0.000 0.015 0.019 0.966
contact-primary-school 98,621 0.000 0.012 0.014 0.974
music-rap-genius 70,057 0.028 0.221 0.141 0.611

63. We still have variety with only 3-node simplices.
63
music-rap-genius
NDC-substances
NDC-classes
DAWN
coauth-DBLP
coauth-MAG-geology
coauth-MAG-history
congress-bills
congress-committees
tags-stack-overflow
tags-math-sx
tags-ask-ubuntu
email-Eu
email-Enron
threads-stack-overflow
threads-math-sx
threads-ask-ubuntu
contact-high-school
contact-primary-school
10 5
10 4
10 3
10 2
10 1
Edge density in projected graph
0.00
0.25
0.50
0.75
1.00
Fractionoftrianglesopen
Exactly 3 nodes per simplex

64. 1
2+1
1
2+
1
1
1
1
2+
2+
2+
1
1
2+
2+
1
2+
2+
2+
245,996
74,219
14,541
7,575
5,781
773
3,560
952
445
389
618
285
2,732,839
157,236
66,644
7,987
8,844
328
3,171
779
722
285
We can also study temporal dynamics in aggregate.
64
Coauthorship data of scholars publishing in history.
Wij = # of simplices containing nodes i and j.
Most groups formed have no previous interaction.
Open triangle of all weak
ties more likely to form a
strong tie before closing.

65. Simplicial closure probability on 4 nodes has similar
behavior to those with 3 nodes,just“up one dimension”.
65
Take first 80% of the data (in time), record the configuration of every 4 nodes,
and compute the fraction that simplicially close in the final 20% of the data.
Increased edge density
increases closure probability.
Increased simplicial tie strength
increases closure probability.
Tension between
simplicial density and
simplicial tie strength.

66. We collected many datasets of timestamped simplices,
where each simplex is a subset of nodes.
66
1. Coauthorship in different domains.
2. Emails with multiple recipients.
3. Tags on Q&A forums.
4. Threads on Q&A forums.
5. Contact/proximity measurements.
6. Musical artist collaboration.
7. Substance makeup and
classification codes applied to
drugs the FDA examines.
8. U.S. Congress committee
memberships and bill sponsorship.
9. Combinations of drugs seen in
patients in ER visits. https://math.stackexchange.com/q/80181
bit.ly/sc-holp-data