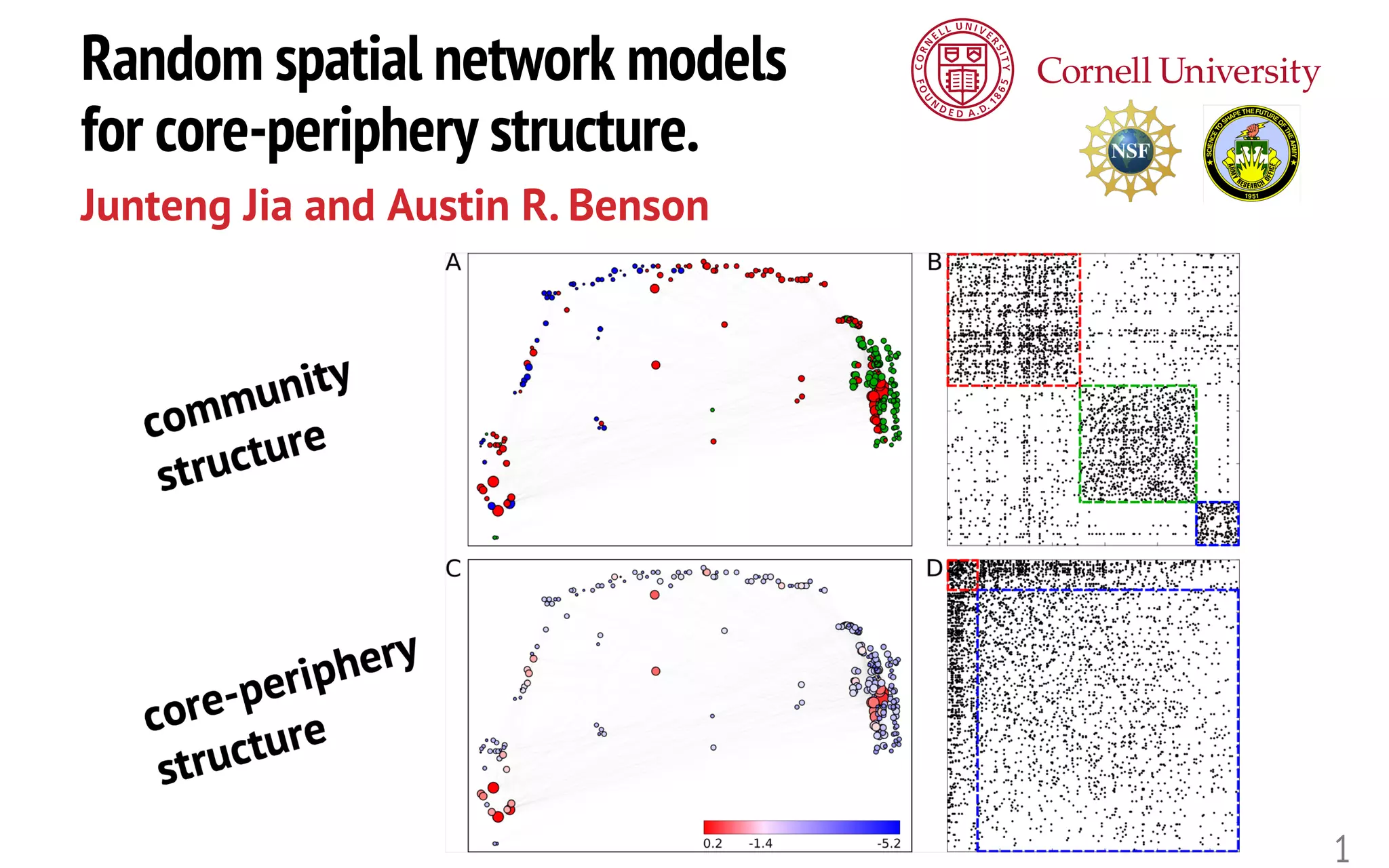
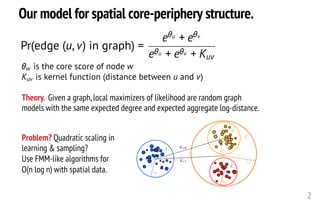
The document proposes a random spatial network model for generating networks with core-periphery structure. The model assigns each node u a weight e^θu and the probability of an edge between nodes u and v is proportional to e^θu + e^θv. This leads to dense connections between high-weight core nodes and sparser connections between core and low-weight peripheral nodes.