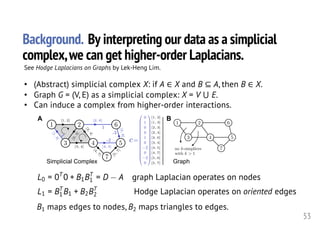
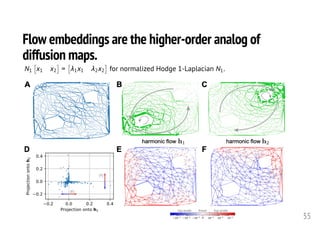
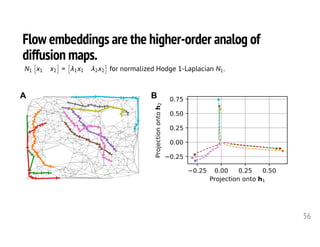
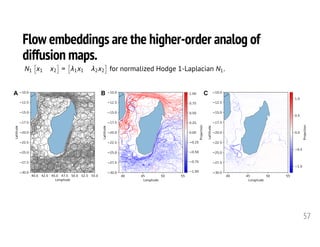
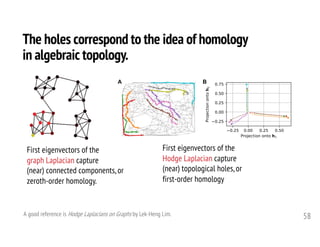
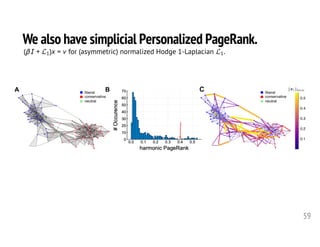
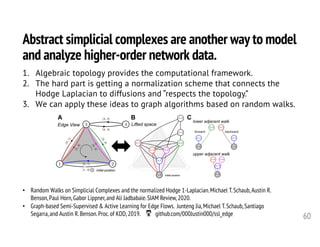
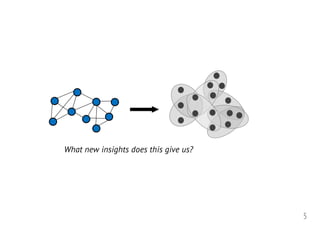
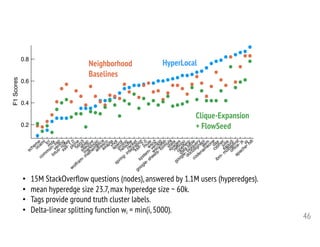
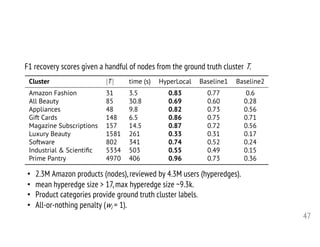
1. The document discusses computational frameworks for analyzing higher-order network data, where interactions can involve more than two nodes. Real-world systems often involve higher-order interactions that are reduced to pairwise connections.
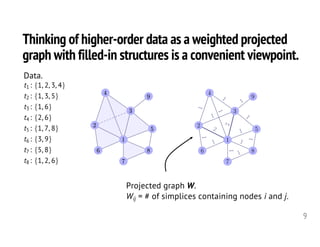
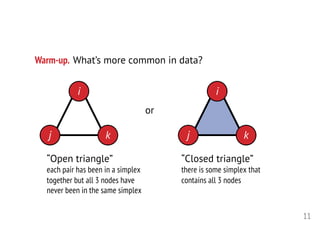
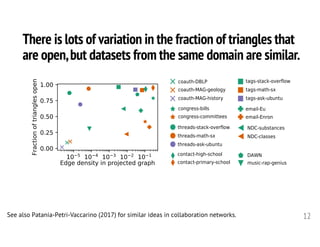
2. The author presents several datasets involving higher-order interactions and shows that predicting the formation of new higher-order connections is similar to link prediction but considers groups of nodes rather than individual links. Structural properties like edge density and tie strength influence the likelihood of simplicial closure.
3. Models are proposed to score open simplices based on structural features and predict which will transition to closed simplices. Accounting for higher-order structure provides new insights beyond traditional network analysis of pairwise connections.







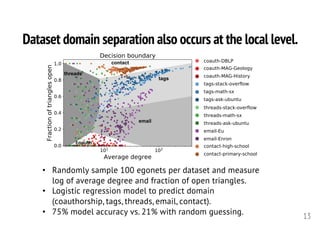


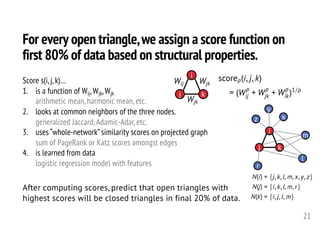
![Simplicial closure depends on structure in projected graph.
17
• First 80% of the data (in time) ⟶ record configurations of triplets not in closed triangle.
• Remainder of data ⟶ find fraction that are now closed triangles.
Increased edge density
increases closure probability.
Increased tie strength
increases closure probability.
Tension between edge
density and tie strength.
Left and middle observations are consistent with theory and empirical studies of social networks.
[Granovetter 73; Kossinets-Watts 06; Backstrom+ 06; Leskovec+ 08]
Closure probability Closure probability Closure probability](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-17-320.jpg)

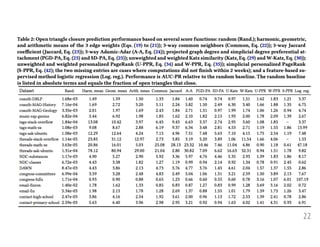

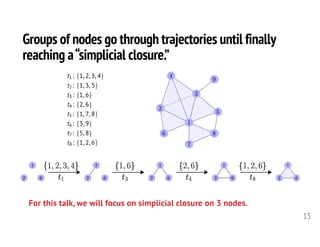
![Generalized means of edges weights are often good
predictors of new 3-node simplices appearing.
24
music-rap-genius
NDC-substances
NDC-classes
DAWN
coauth-DBLP
coauth-MAG-geology
coauth-MAG-history
congress-bills
congress-committees
tags-stack-overflow
tags-math-sx
tags-ask-ubuntu
email-Eu
email-Enron
threads-stack-overflow
threads-math-sx
threads-ask-ubuntu
contact-high-school
contact-primary-school
harmonic geometric arithmetic
p
4 3 2 1 0 1 2 3 4
0
20
40
60
80
Relativeperformance
4 3 2 1 0 1 2 3 4
p
2.5
5.0
7.5
10.0
12.5
Relativeperformance
4 3 2 1 0 1 2 3 4
p
1.0
1.5
2.0
2.5
3.0
3.5
Relativeperformance
Good performance from this local information is a deviation from classical link prediction, where
methods that use long paths (e.g., PageRank) perform well [Liben-Nowell & Kleinberg 07].
For structures on k nodes, the subsets of size k-1 contain rich information only when k > 2.
i
j k
Wij
Wjk
Wjk
i
j k
?
scorep(i, j, k)
= (Wp
ij + Wp
jk + Wp
ik)1/p
<latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit><latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit><latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit><latexit sha1_base64="wECyDT1irjpegMdv/Iox6i4U4iU=">AAAHdXicfVVtb9s2EFa7Lem0t7T7OAxglzlIO/ktXZZkQAADK4oVa7FsdpoCoZtR0sliTEoqSTV2Cf2o/Zph37Zfsa872k5jOdkI2DqR99zDu3tIhYXg2nQ6f966/d77H6yt3/nQ/+jjTz79bOPuvRc6L1UEx1EucvUyZBoEz+DYcCPgZaGAyVDASTj+wa2fvAGleZ4NzLSAoWSjjCc8YganzjZ+2qIGJsbqKFdQnRXbPCDnARk/IJT6W/R1yWJySLZPziw/r14V5BuC5vn4ncmd+eCV7baL6mxjs9PqzAa5bnQXxqa3GEdnd9fu0TiPSgmZiQTT+rTbKczQMmV4JKDyaamhYNGYjeAUzYxJ0EM7y7oiDZyJSZIr/GWGzGb9ZQjGUWxai2INC0vB1KQ+G+b5GFd05dcpTbI/tDwrSgNZNGdMSkFMTlwtScwVREZMSZ3W8PHbIOMRJIpFAZNaMpMGBXfbDMz4bXOkWJEGko0hAiGupuabcnDBQ8XU1GWQX+ggxMgjlZdZrIOCGQMq04g3ik8CnbICdJBwE0RMRO49dphC5EYyNdb/FbUlwTBcnBVOgLGDMjHwK8SVVRDf3+/cDwXyLnuYFEYKIKvs7OF8LlJuYMUnFCVU1v0vefgNkhpT6O/bbVRcSxuMDZMoZdkIWlEu269L0E6Uut39bvdg56CtQXLUbohSlc0LbtKmS6LJs2aICgc183u0tzl/+NQVlOEJcPXx6UjkIRMUX6mD9SDTpYJenAvsfw/1H+UxHFIFgk0usTluvq6h00F3aF3jnABqXT4a9FnmiqsggwtMQLIstjRhkotpDAkrhaks1cmlXReJTpwqKr+xTKaxgxAfdloHQSQ5kqIsBCoeCcxEJy5EPUmMTTMzcaF6c7DVD0/xqO0Oq9WkHgOeMQX9qQxz8QRTsvMourI/P39W2cxRSF5ZWVmO26V9MDc540S8CgkXkAWHA/TLENtpStfSmwlWGfpPnruSXBIMurXy2XBSWS2uSJzzHG2foqerARNFyqqrrf72dKXq8UgAj9LmvPY3rWCjNd4u9etBujDLXZZ9PpLIROeqcuEsDaWl8/nqmizkM7yT45sQi4WqTvGQTkKmTlF8NA3ziaVv3H/Dp6kqBZAU+Cg1eLnu7RaGNMggBcIiUzJBEObTMd4QndbOLkwa5HI0yGP8nrAsAhKCucDz63wJkhE9K6M/p2r4hMwCNDutLsjGJbqf5gqrw7MRyTOCoiICEkM0j8EhlvLa7FbvguD9/+h/g6hZJrMolasCfkW6q9+M68aLnVYXt/fLt5u9/cX35I73hfeVt+11vT2v5/3oHXnHXuT97v3h/eX9vfbP+pfrX69vzV1v31pgPvdqY739L4qSnVk=</latexit>](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-24-320.jpg)
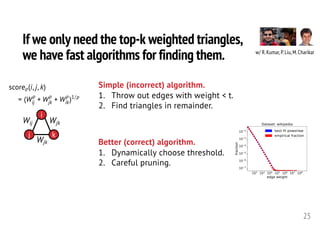
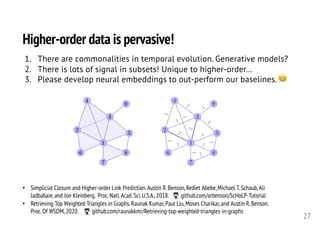

![Graph minimum s-t cuts are fundamental.
29
minimizeS⇢V cut(S)
subject to s 2 S, t /2 S.<latexit sha1_base64="xm7lCa+sznQv4hBLJYdds1WJ/eg=">AAAHn3icfVVtb9s2EFa6rW61t3T9uC/MAg9dITt2uizJhgIGVnQr0G7Z7KQdQiOjpJPEmaQ0kmrsCPqh26/Z0XIWy80mwBZ1vOee48M7MiwEN3Yw+Gvrznvvf3C3c+++/+FHH3/y6faDz85MXuoITqNc5PpNyAwIruDUcivgTaGByVDA63D2vZt//Ra04bma2EUBU8lSxRMeMYumi21LQ0i5qpjWbFFXQtQ+lVxxya/gohoTasrQgCVnNfmSUAtzW0WlrR+NvyKU+o0BXf6AyBKbE+dlCOWKjAP6HbGEqty6r75PQcUrmovt3UF/sHzIu4PharDrrZ6Tiwd3H9I4j0oJykaCGXM+HBR2iuEsjwRgzqWBgkUzlsI5DhWTYKbVUp6adNESkyTX+FOWLK3+OmSVVstkWVgKpudta5jnM5wxte+3OW1yNK24KkoLKmook1I4SZzqJOYaFRIL0ua1fHYVKB5BolkUMGkks1lQcJdnYGdXvVSzIgskm0EEQtyYmqwcXPBQM71wS8gvTRBi5FTnpYpNUDBrQSuDeKv5PDAZK8AECbdBxETkvmOHKURuJdMz819R+xIsw8mlcgJsNSkTC79CXFca4p2jwU4okHfdw2aQagBVV8uX87nMuIUNn1CUUFfuf83D75LM2sJ8u7eH9dU3FmPDPMqYSqEf5XLvzxKMK1+zN/zm4Hj/eM+A5FjlIRa17F1ym/XcInpc9ULsBdBLvyeHu80LKxwFZdgrTh+fpiIPmaD4SR1sBMqUGkZxLrAARtgpUR7DU6pBsPk1Nsfk20V0PhlOK7dxrgBau3wyGTPlxNWg4BIXIBm2Ak2Y5GIRQ8JKYeuKmuR63C4Sk7iqqP3uOpnBHYT46aB/HETYrxbVZgJLHgns3CQuRHuRGJsqO3ehRg24Mo/PsdcOpvXmop4BNpmG8UKGuXiOS6qaKKaufn71sq6Uo5C8rmRdcUyXjsHe5oyGeBMSriArDgcY4xGDR1fptvR2gk2G8fNXTpJrgsmwJV8VzuvKiBsS59ygqxfo6TRgoshYfZPq7y82VI9TATzKeo32t83gRhs8Xtrng3Rh1ndZjnkqkYk2VeXCVTSUFW3s9TtlIV/i6R3fhlhN1G2Kx3QeMn2OxUezMJ9X9K377/o006UAkgFPM4un6+FBYUmXTDIgLLIlEwRhPp3hCTHo7x/AvEuuny55hjcPUxGQEOwl9q/zJUhGzFJGv6Hq+oQsA/QG/SHI7jV6nOUa1eEqJbkiWFREQGKJ4TE4xNq6dof1v0HwAnjyv0H0ciXLKLVTAa+R4eal8e7gbL8/xPR++Xp3dLS6UO55n3tfeI+8oXfojbwfvRPv1Iu8v7e8rftbfmen80Pnp85J43pna4V56LWezm//AOeeq5s=</latexit><latexit sha1_base64="xm7lCa+sznQv4hBLJYdds1WJ/eg=">AAAHn3icfVVtb9s2EFa6rW61t3T9uC/MAg9dITt2uizJhgIGVnQr0G7Z7KQdQiOjpJPEmaQ0kmrsCPqh26/Z0XIWy80mwBZ1vOee48M7MiwEN3Yw+Gvrznvvf3C3c+++/+FHH3/y6faDz85MXuoITqNc5PpNyAwIruDUcivgTaGByVDA63D2vZt//Ra04bma2EUBU8lSxRMeMYumi21LQ0i5qpjWbFFXQtQ+lVxxya/gohoTasrQgCVnNfmSUAtzW0WlrR+NvyKU+o0BXf6AyBKbE+dlCOWKjAP6HbGEqty6r75PQcUrmovt3UF/sHzIu4PharDrrZ6Tiwd3H9I4j0oJykaCGXM+HBR2iuEsjwRgzqWBgkUzlsI5DhWTYKbVUp6adNESkyTX+FOWLK3+OmSVVstkWVgKpudta5jnM5wxte+3OW1yNK24KkoLKmook1I4SZzqJOYaFRIL0ua1fHYVKB5BolkUMGkks1lQcJdnYGdXvVSzIgskm0EEQtyYmqwcXPBQM71wS8gvTRBi5FTnpYpNUDBrQSuDeKv5PDAZK8AECbdBxETkvmOHKURuJdMz819R+xIsw8mlcgJsNSkTC79CXFca4p2jwU4okHfdw2aQagBVV8uX87nMuIUNn1CUUFfuf83D75LM2sJ8u7eH9dU3FmPDPMqYSqEf5XLvzxKMK1+zN/zm4Hj/eM+A5FjlIRa17F1ym/XcInpc9ULsBdBLvyeHu80LKxwFZdgrTh+fpiIPmaD4SR1sBMqUGkZxLrAARtgpUR7DU6pBsPk1Nsfk20V0PhlOK7dxrgBau3wyGTPlxNWg4BIXIBm2Ak2Y5GIRQ8JKYeuKmuR63C4Sk7iqqP3uOpnBHYT46aB/HETYrxbVZgJLHgns3CQuRHuRGJsqO3ehRg24Mo/PsdcOpvXmop4BNpmG8UKGuXiOS6qaKKaufn71sq6Uo5C8rmRdcUyXjsHe5oyGeBMSriArDgcY4xGDR1fptvR2gk2G8fNXTpJrgsmwJV8VzuvKiBsS59ygqxfo6TRgoshYfZPq7y82VI9TATzKeo32t83gRhs8Xtrng3Rh1ndZjnkqkYk2VeXCVTSUFW3s9TtlIV/i6R3fhlhN1G2Kx3QeMn2OxUezMJ9X9K377/o006UAkgFPM4un6+FBYUmXTDIgLLIlEwRhPp3hCTHo7x/AvEuuny55hjcPUxGQEOwl9q/zJUhGzFJGv6Hq+oQsA/QG/SHI7jV6nOUa1eEqJbkiWFREQGKJ4TE4xNq6dof1v0HwAnjyv0H0ciXLKLVTAa+R4eal8e7gbL8/xPR++Xp3dLS6UO55n3tfeI+8oXfojbwfvRPv1Iu8v7e8rftbfmen80Pnp85J43pna4V56LWezm//AOeeq5s=</latexit><latexit sha1_base64="xm7lCa+sznQv4hBLJYdds1WJ/eg=">AAAHn3icfVVtb9s2EFa6rW61t3T9uC/MAg9dITt2uizJhgIGVnQr0G7Z7KQdQiOjpJPEmaQ0kmrsCPqh26/Z0XIWy80mwBZ1vOee48M7MiwEN3Yw+Gvrznvvf3C3c+++/+FHH3/y6faDz85MXuoITqNc5PpNyAwIruDUcivgTaGByVDA63D2vZt//Ra04bma2EUBU8lSxRMeMYumi21LQ0i5qpjWbFFXQtQ+lVxxya/gohoTasrQgCVnNfmSUAtzW0WlrR+NvyKU+o0BXf6AyBKbE+dlCOWKjAP6HbGEqty6r75PQcUrmovt3UF/sHzIu4PharDrrZ6Tiwd3H9I4j0oJykaCGXM+HBR2iuEsjwRgzqWBgkUzlsI5DhWTYKbVUp6adNESkyTX+FOWLK3+OmSVVstkWVgKpudta5jnM5wxte+3OW1yNK24KkoLKmook1I4SZzqJOYaFRIL0ua1fHYVKB5BolkUMGkks1lQcJdnYGdXvVSzIgskm0EEQtyYmqwcXPBQM71wS8gvTRBi5FTnpYpNUDBrQSuDeKv5PDAZK8AECbdBxETkvmOHKURuJdMz819R+xIsw8mlcgJsNSkTC79CXFca4p2jwU4okHfdw2aQagBVV8uX87nMuIUNn1CUUFfuf83D75LM2sJ8u7eH9dU3FmPDPMqYSqEf5XLvzxKMK1+zN/zm4Hj/eM+A5FjlIRa17F1ym/XcInpc9ULsBdBLvyeHu80LKxwFZdgrTh+fpiIPmaD4SR1sBMqUGkZxLrAARtgpUR7DU6pBsPk1Nsfk20V0PhlOK7dxrgBau3wyGTPlxNWg4BIXIBm2Ak2Y5GIRQ8JKYeuKmuR63C4Sk7iqqP3uOpnBHYT46aB/HETYrxbVZgJLHgns3CQuRHuRGJsqO3ehRg24Mo/PsdcOpvXmop4BNpmG8UKGuXiOS6qaKKaufn71sq6Uo5C8rmRdcUyXjsHe5oyGeBMSriArDgcY4xGDR1fptvR2gk2G8fNXTpJrgsmwJV8VzuvKiBsS59ygqxfo6TRgoshYfZPq7y82VI9TATzKeo32t83gRhs8Xtrng3Rh1ndZjnkqkYk2VeXCVTSUFW3s9TtlIV/i6R3fhlhN1G2Kx3QeMn2OxUezMJ9X9K377/o006UAkgFPM4un6+FBYUmXTDIgLLIlEwRhPp3hCTHo7x/AvEuuny55hjcPUxGQEOwl9q/zJUhGzFJGv6Hq+oQsA/QG/SHI7jV6nOUa1eEqJbkiWFREQGKJ4TE4xNq6dof1v0HwAnjyv0H0ciXLKLVTAa+R4eal8e7gbL8/xPR++Xp3dLS6UO55n3tfeI+8oXfojbwfvRPv1Iu8v7e8rftbfmen80Pnp85J43pna4V56LWezm//AOeeq5s=</latexit><latexit sha1_base64="xm7lCa+sznQv4hBLJYdds1WJ/eg=">AAAHn3icfVVtb9s2EFa6rW61t3T9uC/MAg9dITt2uizJhgIGVnQr0G7Z7KQdQiOjpJPEmaQ0kmrsCPqh26/Z0XIWy80mwBZ1vOee48M7MiwEN3Yw+Gvrznvvf3C3c+++/+FHH3/y6faDz85MXuoITqNc5PpNyAwIruDUcivgTaGByVDA63D2vZt//Ra04bma2EUBU8lSxRMeMYumi21LQ0i5qpjWbFFXQtQ+lVxxya/gohoTasrQgCVnNfmSUAtzW0WlrR+NvyKU+o0BXf6AyBKbE+dlCOWKjAP6HbGEqty6r75PQcUrmovt3UF/sHzIu4PharDrrZ6Tiwd3H9I4j0oJykaCGXM+HBR2iuEsjwRgzqWBgkUzlsI5DhWTYKbVUp6adNESkyTX+FOWLK3+OmSVVstkWVgKpudta5jnM5wxte+3OW1yNK24KkoLKmook1I4SZzqJOYaFRIL0ua1fHYVKB5BolkUMGkks1lQcJdnYGdXvVSzIgskm0EEQtyYmqwcXPBQM71wS8gvTRBi5FTnpYpNUDBrQSuDeKv5PDAZK8AECbdBxETkvmOHKURuJdMz819R+xIsw8mlcgJsNSkTC79CXFca4p2jwU4okHfdw2aQagBVV8uX87nMuIUNn1CUUFfuf83D75LM2sJ8u7eH9dU3FmPDPMqYSqEf5XLvzxKMK1+zN/zm4Hj/eM+A5FjlIRa17F1ym/XcInpc9ULsBdBLvyeHu80LKxwFZdgrTh+fpiIPmaD4SR1sBMqUGkZxLrAARtgpUR7DU6pBsPk1Nsfk20V0PhlOK7dxrgBau3wyGTPlxNWg4BIXIBm2Ak2Y5GIRQ8JKYeuKmuR63C4Sk7iqqP3uOpnBHYT46aB/HETYrxbVZgJLHgns3CQuRHuRGJsqO3ehRg24Mo/PsdcOpvXmop4BNpmG8UKGuXiOS6qaKKaufn71sq6Uo5C8rmRdcUyXjsHe5oyGeBMSriArDgcY4xGDR1fptvR2gk2G8fNXTpJrgsmwJV8VzuvKiBsS59ygqxfo6TRgoshYfZPq7y82VI9TATzKeo32t83gRhs8Xtrng3Rh1ndZjnkqkYk2VeXCVTSUFW3s9TtlIV/i6R3fhlhN1G2Kx3QeMn2OxUezMJ9X9K377/o006UAkgFPM4un6+FBYUmXTDIgLLIlEwRhPp3hCTHo7x/AvEuuny55hjcPUxGQEOwl9q/zJUhGzFJGv6Hq+oQsA/QG/SHI7jV6nOUa1eEqJbkiWFREQGKJ4TE4xNq6dof1v0HwAnjyv0H0ciXLKLVTAa+R4eal8e7gbL8/xPR++Xp3dLS6UO55n3tfeI+8oXfojbwfvRPv1Iu8v7e8rftbfmen80Pnp85J43pna4V56LWezm//AOeeq5s=</latexit>
1 3
2 4
5
6
7
8
s
t
• Maximum flow / min s-t cut [Ford, Fulkerson, Dantzig 1950s]
• Densest subgraph [Goldberg 84; Shang+ 18]
• Graph-based semi-supervised learning algorithms [Blum-Chawla 01]
• Local graph clustering [Andersen-Lang 08; Oreccchia-Zhu 14; Veldt+ 16]
poly-time algorithms!](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-29-320.jpg)

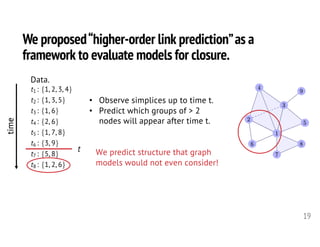
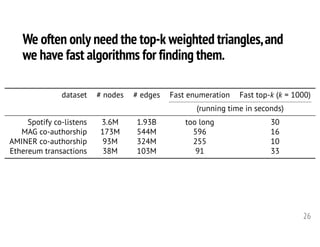
![What is a hypergraph minimum s-t cut?
31
s
t
Should we treat the 2/2 split
differently from the 1/3 split?
Historically, no. [Lawler 73, Ihler+ 93]
More recently, yes.
[Li-Milenkovic 17, Veldt-Benson-Kleinberg 20]
edge in a graph size-3 hyperedges
“Only one way to split a triangle”
[Benson+ 16; Li-Milenkovic 17; Yin+ 17]
Must be split 1/1.](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-31-320.jpg)
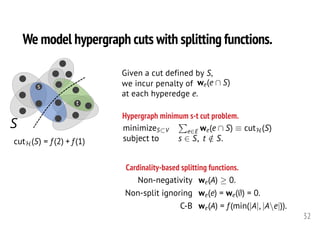
![Cardinality-based splitting functions appear
throughout the literature.
33
[Lawler 73; Ihler+ 93; Yin+ 17]
[Hu-Moerder 85; Heuer+ 18]
[Agarwal+ 06; Zhou+ 06; Benson+ 16]
[Yaros- Imielinski 13]
[Li-Milenkovic 18]
<latexit sha1_base64="gX/87S67KKdqKR6T9Qjl8vcDiHo=">AAAJt3icfVZbb9s2FHbTrau9W7s97oVd4qHbZMdOl7UZUCDBimIFWqxd0gsQehklHVmESVElqdoewx/aX7MdynJrO2n1YFHk+b5zP3RcCm7sYPD2ytbVTz699tn1dufzL7786usbN795YVSlE3ieKKH0q5gZELyA55ZbAa9KDUzGAl7Gk9/D+cs3oA1XxYmdlzCSbFzwjCfM4tbZzS1NYxjzwlkWV4Jp74TwHUKOhOgp3SuUzXkxJj+QHfpmega3j34k90kDSVCv8WSAp9TCzDqekZ0jQnlBqIOIUJClnRuw1O94QikZvpNEWtBTbsBTKNKGaYeg0OkvUo7QgMfoENOkhIIJO980QNY6yPnReUTOAQ1iycQIZnJydE6oJzsrTM8qlmp0N/kA2XmAJKmym0SrJA+4SVRVWJJU9sPG/E2ZKHN20abmYGHaqpe9J8RUsVRpCP4mcaZZ4obe7Xny89pXbW6tmArIcOWGUSNABabbEkyDDgvvCBWZUEqTpQkLAWgE8FUf+w0CWLX/HdnHuRoq4tFFzce5bfzt1EleVljn7Mb2oD+oH3JxMWwW263meXp281pEU5VUEgqboEXmdDgo7cgxjVkV4Du0MlCiuWwMp7gsmAQzcnV3eNLFnZRkaFemQgLDbmcVgjyazddYlsbO1ndjpSZ4Yvwa/jQ0nykqGYOGNNKVgBSNE2Oluc3lHmyIVza7N3K8KCsLRbIwMKsEsYqEFiUp15BYMSfrVlo++TcqeAIhTRGTRjKbRyUPXkWSTSCB0LsBEkQFjzXT8+CcmpooZHOssYRTE5XMWtCFQZTVfBaZnJVgoozbKGEiCd9pwJRCWcn0xHyItS/BMjysYyrAupMqs/AXpN5hJG7dG9yKBepdlcDGH2uAwrv6FWSmObewIROLCrwLvysSnS7JrS3Nb7u7OEX6xiI3zJKcFWPoJ0ruvq7AhLlmdoe/7h/sHewakBwrM8b2l70pZqMXnOjxohfjkARdy925u714dWgII8MhGuLToWOhYiawxSwNsEMoTKXhMFUCS+MQR2iiUrhPNQg2W2Lrybae75PhyIUkhWSvZfTpyTErQnA1FDBFByTDPqEZk1zMU8hYJULPmWy5Xi8Ik4UK8J3uqjKDGYT0/qB/ECU4HyxGmwlsBlRgZyYLFOtOIjct7CxQHS7Azvx0il24P/KbTj0AbD8Nx3MZK/EQXXILFuPdn08ee1cEFZJ7J73jaC49BnuZMG6km5C4gTQ6AuC4ijGdtgopvVzBpobjh09CSJYKToZr4XPxzDsj3isJwgu0e4SSIQb1YPPvTf3n0UbU07EAnuS9RewvO8FEGxw865NDBprVLMtjPpaoiS6qKtA5GktHF/v+QlnIx3itp5chmgO/ruInOouZPsXio3msZo6+Cb/dDs3DhCI51BN60L+7X1rSJSc5EJbYigmCsA6d4IQY9Pf2YdYly6cb7kHLigRIDHaK/RtkCSojpg5jZ6Gqi1dbTdAb9Icgu0v0ca40Rif8o1AFwaIi9fVleAoBseLX9tC/I8Gr4c5HSRZ3Tc2CQfB4vww3b5OLixd7/eF+f/Bsb/vwXnPTXG991/q+dbs1bN1tHbb+aD1tPW8lW2+3/rt6/Wq7fdA+a2ftfCG6daXBfNtae9qv/wf+EGQx</latexit>
All-or-nothing we(A) =
(
0 if A 2 {e, ;}
1 otherwise
Linear penalty we(A) = min{|A|, |eA|}
Quadratic penalty we(A) = |A| · |eA|
Discount cut we(A) = min{|A|↵ , |eA|↵ }
L-M submodular we(A) = 1
2 + 1
2 · min
n
1, |A|
b↵|e|c , |eA|
b↵|e|c
o](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-33-320.jpg)
![We solve hypergraph cut problems with graph reductions.
34
1/21/2
1/2
1
1
1
1
∞
∞ ∞
∞
∞∞
Gadgets (expansions) model a hyperedge with a small graph.
clique expansion star expansion Lawler gadget [1973]hyperedge
In a graph reduction, we first replace all hyperedges with graph gadgets...
s
t
s
t
s
t
s
t
… then solve the (min s-t cut) problem exactly on the graph,
and finally convert the solution to a hypergraph solution.
Quadratic penalty
f(i) = i ( |e| – i )
Linear penalty
f(i) = i
All-or-nothing
f(0) = 0,o/w f(i) = 1](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-34-320.jpg)
![b
We made a new gadget for C-B splitting functions.
35
This gadget models min(|A|, |eA|, b).
Theorem [Veldt-Benson-Kleinberg 20a]. Nonnegative linear combinations of the
C-B gadget can model any submodular cardinality-based splitting function.
See also Graph Cuts for Minimizing Robust Higher Order Potentials,Kohli et al.,2008.
<latexit sha1_base64="beQz4cdyY+p8N+9L01TDcNAiwcQ=">AAAHvnicfVVbb9s2FFa6rem8S9PtcS/sAg9JIDt2iizJgADuWhQr0GLZnLQFzCClpCOJMElpJBXLJfRD97afskNf2tjJRkASRZ7vO3cyKgU3ttf7e+PeZ59/cX/zwZetr77+5tuHW4++e2OKSsdwERei0O8iZkBwBReWWwHvSg1MRgLeRuNnfv/tNWjDC3VupyVcSpYpnvKYWVy62vpAI8i4ckzwTO01LWqhtu5Z59eG/ERzU7IYXK97cBjLhtDryRXsPN0lpyTdoZKrHSqQ25KnhGo/CcliAQiNWDw2gpn84+7ubrdFQSVLXVdb271ubzbI7Ul/MdkOFuPs6tH9kCZFXElQNkZqM+r3SnvpmLY8FoDGVwbQ4jHLYIRTxSSYSzcLUkPauJKQtND4KEtmq62bEOTRbLrC4iyLKsF0vboaFcUYd0yzgh/5HBhVyQg0JKGuBCRonMgKzW0uD2BNvLLp8aXjqqwsqHhuYFoJYgviM0USriG2YkpWrbR8/CFUPIZUszhk0khm87Dk3qtQsjHEIMTcXi8qeKSZnnrniokJfVoyXVQqMWHJrAWtDKKs5nVoclaCCVNuw5iJ2P8nHlOKwkqmx+a/WLsSLMPNWUwFWHdepRb+hKRxGInHx73HkUC9NyVsDpkGUI2bfbzMJOcW1mQiUUHj/PuGRKtNcmtL88v+PlZr11jkhjrOmcqgGxdy/68KjC9vs9//+fDk4GTfgORYghEWvexMMBsd70SHq06EvQJ6JvfkaHv+aVEfRoa95OPTopkoIiYo/lIPG4AylYZBUggsjQF2UlwkcEo1CFYvsQUav1peo/P+pfNJ8sleyejZ+ZApH1wNCibogGTYJTRlkotpAimrhG0cNelyvloQJvUV0LTaN5UZzCAkp73uSRhjp1qMNhPYDKjA1ib1FKtOIjdVtvZUgznYmb0RduHhZbPu1HPA9tMwnMqoEC/QJTdnMY37/fWrximvQvLGycZxNJcOwd4ljAvJOiRaQBY6PGBYRZhOW/mU3q1gXcPwxWsfkqWC8/5K+FxUN86IT0q88BztXqKkjwETZc6aT6a+f7kW9SQTwOO8M4/9XTuYaIMHz+rJIT3NzSzLIc8kaqLzqvJ0jkbS0fl6c6ss5Cs83ZO7EIuNZlXFHq0jpkdYfDSPitrRa/9ut2juTyiSA89yi+fu0WFpSZuc50BYbCsmCMJadIwnhL8AoG6T5WiT53gzMRUDicBOsH+9LEFlxMzC2JqrarcImRF0et0+yPYSPcwLjdHhKiOFIlhUREBqieEJeMQNv7b7zUcSvBqe/C+JnnkyY8Eg+Pulv36b3J68Oej2D7u9Pw62B8eLm+ZB8EPwY7AT9IOjYBD8FpwFF0Ec/LNxf+PhxtbmYDPdlJvFXPTexgLzfbAyNut/AfzCt34=</latexit>
C-B we(A) = f (min(|A|, |eA|)).
(F is submodular on X if F(A B) + F(A [ B) F(A) + F(B) for any A, B ✓ X.)<latexit sha1_base64="jx6llVBabtrhi3TShW9c6Ptv2Kc=">AAAHkXicfVXfb9s2EFa7re60H02Xx72wiw0knezYKbIkAwq4WRGsWItls9MGiIyMkk4WYZJSSaqxK+g/3D+wf2Ov28OOkrNYbjY9SNTxvvt4x4/HIONMm37/jzt3P/r4k3ut+5+6n33+xZcPNh5+9VqnuQrhLEx5qs4DqoEzCWeGGQ7nmQIqAg5vgtkPdv7NO1CapXJsFhlMBJ1KFrOQGjRdbsTb7ZM2YZroPBBplHOqSCpJ+xyNMWmfbD8jfkgzcrxDviX1X179+RzeWkNtP95pkzhVhMoFaT/zyDHxMaAGg07n7d7O5cZWv9evHvLhYLAcbDnL5/Ty4b1NP0rDXIA0IadaXwz6mZkUVBkWcihdP9eQ0XBGp3CBQ0kF6ElRFaQkHbRE1YLiVBpSWd1VCMZRdNGIUhga2PTnTWuQpjOc0aXrNjlNfDgpmMxyAzKsKeOcE5MSW2cSMQWh4QvS5DVs9t6TLIRY0dCjQgtqEi9jdp2emb3vThXNEk/QGYTA+Y2pXpWFcxYoqhY2hfRKewFGnqo0l5H2MmoMKKkRbxSbezqhGWgvZsYLKQ/tf2QxGU+NoGqm/ytqT4ChOFlVjoMpxnls4FeIykJB9Oiw/yjgyLvqYRKYKgBZFtXH+lwlzMCaT8BzKAv7XvFwOyQxJtPf7+4amPe0wdgwDxMqp9ALU7H7NgdtBat3B9/tH+0d7WoQDHUdoIxF94qZpGuT6DLZDVD9oCq/Jwdb9cf1bUEpng5bH9ef8jSgHCVsfAsbgtS5gmGUchTAEM9GmEbw1FfA6fwam+LimyK6GA8mhd04K4DGLp+OR1Ta4iqQcIUJCCqjwo+pYHwRQUxzbsrC1/H1uCkSHVtVlG5nlUzjDkL0tN878kLBkBRlwVHySGDmOrYhmklibF+auQ01rMGFfnyBZ21/Uq4n9RzwkCkYLUSQ8hNMqaij6LL4+dXLspCWQrCyEGXBcLn+CMxtzmiI1iHBErLksIAR9gZsVrnd0tsJ1hlGJ69sSa4JxoNG+YpgXhaa35BY5xpdvEBPWwPKs4SWN0v97cVa1aMpBxYm3br2t83gRmtsL83+IGyY1V0WIzYVyOTXqrLhCj8QhV/byw9kIV5iv45uQywnyibFY38eUHWB4vOTIJ0X/jv77rh+onIOJAE2TQx214P9zJAOGSdAaGhyygnCXH+GHaLf29uHeYdcPx3yHO8aKkMgAZgrPL/WF9t5RHRVRrem6riEVAG6/d4AROcaPUpShdVhcmpvDxQV4RAbolkEFrGS19ag/DcIXgBP/jeIqjKpopS2CniNDNYvjQ8Hr/d6A1zeL3tbw8PlhXLf+dr5xtl2Bs6BM3R+dE6dMyd0fnf+dP5y/m5tto5aw9Zx7Xr3zhKz6TSe1k//AIESoIo=</latexit><latexit sha1_base64="jx6llVBabtrhi3TShW9c6Ptv2Kc=">AAAHkXicfVXfb9s2EFa7re60H02Xx72wiw0knezYKbIkAwq4WRGsWItls9MGiIyMkk4WYZJSSaqxK+g/3D+wf2Ov28OOkrNYbjY9SNTxvvt4x4/HIONMm37/jzt3P/r4k3ut+5+6n33+xZcPNh5+9VqnuQrhLEx5qs4DqoEzCWeGGQ7nmQIqAg5vgtkPdv7NO1CapXJsFhlMBJ1KFrOQGjRdbsTb7ZM2YZroPBBplHOqSCpJ+xyNMWmfbD8jfkgzcrxDviX1X179+RzeWkNtP95pkzhVhMoFaT/zyDHxMaAGg07n7d7O5cZWv9evHvLhYLAcbDnL5/Ty4b1NP0rDXIA0IadaXwz6mZkUVBkWcihdP9eQ0XBGp3CBQ0kF6ElRFaQkHbRE1YLiVBpSWd1VCMZRdNGIUhga2PTnTWuQpjOc0aXrNjlNfDgpmMxyAzKsKeOcE5MSW2cSMQWh4QvS5DVs9t6TLIRY0dCjQgtqEi9jdp2emb3vThXNEk/QGYTA+Y2pXpWFcxYoqhY2hfRKewFGnqo0l5H2MmoMKKkRbxSbezqhGWgvZsYLKQ/tf2QxGU+NoGqm/ytqT4ChOFlVjoMpxnls4FeIykJB9Oiw/yjgyLvqYRKYKgBZFtXH+lwlzMCaT8BzKAv7XvFwOyQxJtPf7+4amPe0wdgwDxMqp9ALU7H7NgdtBat3B9/tH+0d7WoQDHUdoIxF94qZpGuT6DLZDVD9oCq/Jwdb9cf1bUEpng5bH9ef8jSgHCVsfAsbgtS5gmGUchTAEM9GmEbw1FfA6fwam+LimyK6GA8mhd04K4DGLp+OR1Ta4iqQcIUJCCqjwo+pYHwRQUxzbsrC1/H1uCkSHVtVlG5nlUzjDkL0tN878kLBkBRlwVHySGDmOrYhmklibF+auQ01rMGFfnyBZ21/Uq4n9RzwkCkYLUSQ8hNMqaij6LL4+dXLspCWQrCyEGXBcLn+CMxtzmiI1iHBErLksIAR9gZsVrnd0tsJ1hlGJ69sSa4JxoNG+YpgXhaa35BY5xpdvEBPWwPKs4SWN0v97cVa1aMpBxYm3br2t83gRmtsL83+IGyY1V0WIzYVyOTXqrLhCj8QhV/byw9kIV5iv45uQywnyibFY38eUHWB4vOTIJ0X/jv77rh+onIOJAE2TQx214P9zJAOGSdAaGhyygnCXH+GHaLf29uHeYdcPx3yHO8aKkMgAZgrPL/WF9t5RHRVRrem6riEVAG6/d4AROcaPUpShdVhcmpvDxQV4RAbolkEFrGS19ag/DcIXgBP/jeIqjKpopS2CniNDNYvjQ8Hr/d6A1zeL3tbw8PlhXLf+dr5xtl2Bs6BM3R+dE6dMyd0fnf+dP5y/m5tto5aw9Zx7Xr3zhKz6TSe1k//AIESoIo=</latexit><latexit sha1_base64="jx6llVBabtrhi3TShW9c6Ptv2Kc=">AAAHkXicfVXfb9s2EFa7re60H02Xx72wiw0knezYKbIkAwq4WRGsWItls9MGiIyMkk4WYZJSSaqxK+g/3D+wf2Ov28OOkrNYbjY9SNTxvvt4x4/HIONMm37/jzt3P/r4k3ut+5+6n33+xZcPNh5+9VqnuQrhLEx5qs4DqoEzCWeGGQ7nmQIqAg5vgtkPdv7NO1CapXJsFhlMBJ1KFrOQGjRdbsTb7ZM2YZroPBBplHOqSCpJ+xyNMWmfbD8jfkgzcrxDviX1X179+RzeWkNtP95pkzhVhMoFaT/zyDHxMaAGg07n7d7O5cZWv9evHvLhYLAcbDnL5/Ty4b1NP0rDXIA0IadaXwz6mZkUVBkWcihdP9eQ0XBGp3CBQ0kF6ElRFaQkHbRE1YLiVBpSWd1VCMZRdNGIUhga2PTnTWuQpjOc0aXrNjlNfDgpmMxyAzKsKeOcE5MSW2cSMQWh4QvS5DVs9t6TLIRY0dCjQgtqEi9jdp2emb3vThXNEk/QGYTA+Y2pXpWFcxYoqhY2hfRKewFGnqo0l5H2MmoMKKkRbxSbezqhGWgvZsYLKQ/tf2QxGU+NoGqm/ytqT4ChOFlVjoMpxnls4FeIykJB9Oiw/yjgyLvqYRKYKgBZFtXH+lwlzMCaT8BzKAv7XvFwOyQxJtPf7+4amPe0wdgwDxMqp9ALU7H7NgdtBat3B9/tH+0d7WoQDHUdoIxF94qZpGuT6DLZDVD9oCq/Jwdb9cf1bUEpng5bH9ef8jSgHCVsfAsbgtS5gmGUchTAEM9GmEbw1FfA6fwam+LimyK6GA8mhd04K4DGLp+OR1Ta4iqQcIUJCCqjwo+pYHwRQUxzbsrC1/H1uCkSHVtVlG5nlUzjDkL0tN878kLBkBRlwVHySGDmOrYhmklibF+auQ01rMGFfnyBZ21/Uq4n9RzwkCkYLUSQ8hNMqaij6LL4+dXLspCWQrCyEGXBcLn+CMxtzmiI1iHBErLksIAR9gZsVrnd0tsJ1hlGJ69sSa4JxoNG+YpgXhaa35BY5xpdvEBPWwPKs4SWN0v97cVa1aMpBxYm3br2t83gRmtsL83+IGyY1V0WIzYVyOTXqrLhCj8QhV/byw9kIV5iv45uQywnyibFY38eUHWB4vOTIJ0X/jv77rh+onIOJAE2TQx214P9zJAOGSdAaGhyygnCXH+GHaLf29uHeYdcPx3yHO8aKkMgAZgrPL/WF9t5RHRVRrem6riEVAG6/d4AROcaPUpShdVhcmpvDxQV4RAbolkEFrGS19ag/DcIXgBP/jeIqjKpopS2CniNDNYvjQ8Hr/d6A1zeL3tbw8PlhXLf+dr5xtl2Bs6BM3R+dE6dMyd0fnf+dP5y/m5tto5aw9Zx7Xr3zhKz6TSe1k//AIESoIo=</latexit><latexit sha1_base64="jx6llVBabtrhi3TShW9c6Ptv2Kc=">AAAHkXicfVXfb9s2EFa7re60H02Xx72wiw0knezYKbIkAwq4WRGsWItls9MGiIyMkk4WYZJSSaqxK+g/3D+wf2Ov28OOkrNYbjY9SNTxvvt4x4/HIONMm37/jzt3P/r4k3ut+5+6n33+xZcPNh5+9VqnuQrhLEx5qs4DqoEzCWeGGQ7nmQIqAg5vgtkPdv7NO1CapXJsFhlMBJ1KFrOQGjRdbsTb7ZM2YZroPBBplHOqSCpJ+xyNMWmfbD8jfkgzcrxDviX1X179+RzeWkNtP95pkzhVhMoFaT/zyDHxMaAGg07n7d7O5cZWv9evHvLhYLAcbDnL5/Ty4b1NP0rDXIA0IadaXwz6mZkUVBkWcihdP9eQ0XBGp3CBQ0kF6ElRFaQkHbRE1YLiVBpSWd1VCMZRdNGIUhga2PTnTWuQpjOc0aXrNjlNfDgpmMxyAzKsKeOcE5MSW2cSMQWh4QvS5DVs9t6TLIRY0dCjQgtqEi9jdp2emb3vThXNEk/QGYTA+Y2pXpWFcxYoqhY2hfRKewFGnqo0l5H2MmoMKKkRbxSbezqhGWgvZsYLKQ/tf2QxGU+NoGqm/ytqT4ChOFlVjoMpxnls4FeIykJB9Oiw/yjgyLvqYRKYKgBZFtXH+lwlzMCaT8BzKAv7XvFwOyQxJtPf7+4amPe0wdgwDxMqp9ALU7H7NgdtBat3B9/tH+0d7WoQDHUdoIxF94qZpGuT6DLZDVD9oCq/Jwdb9cf1bUEpng5bH9ef8jSgHCVsfAsbgtS5gmGUchTAEM9GmEbw1FfA6fwam+LimyK6GA8mhd04K4DGLp+OR1Ta4iqQcIUJCCqjwo+pYHwRQUxzbsrC1/H1uCkSHVtVlG5nlUzjDkL0tN878kLBkBRlwVHySGDmOrYhmklibF+auQ01rMGFfnyBZ21/Uq4n9RzwkCkYLUSQ8hNMqaij6LL4+dXLspCWQrCyEGXBcLn+CMxtzmiI1iHBErLksIAR9gZsVrnd0tsJ1hlGJ69sSa4JxoNG+YpgXhaa35BY5xpdvEBPWwPKs4SWN0v97cVa1aMpBxYm3br2t83gRmtsL83+IGyY1V0WIzYVyOTXqrLhCj8QhV/byw9kIV5iv45uQywnyibFY38eUHWB4vOTIJ0X/jv77rh+onIOJAE2TQx214P9zJAOGSdAaGhyygnCXH+GHaLf29uHeYdcPx3yHO8aKkMgAZgrPL/WF9t5RHRVRrem6riEVAG6/d4AROcaPUpShdVhcmpvDxQV4RAbolkEFrGS19ag/DcIXgBP/jeIqjKpopS2CniNDNYvjQ8Hr/d6A1zeL3tbw8PlhXLf+dr5xtl2Bs6BM3R+dE6dMyd0fnf+dP5y/m5tto5aw9Zx7Xr3zhKz6TSe1k//AIESoIo=</latexit>](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-35-320.jpg)
![36
Theorem [Veldt-Benson-Kleinberg 20a]. The hypergraph min s-t cut problem
with a cardinality-based splitting function is graph-reducible (via gadgets)
if and only if the splitting function is submodular.
Cardinality-based splitting functions.
s
t
S<latexit sha1_base64="wtJ1SkLACwJOcMcL9/jLEzSB0Ao=">AAAHLHicfVVdj9w0FE0LDCV8tfSRF5ftSKjKfG217C5SpZGoKiq1YmFm20qbUXGSm8Qa2wm2083Uyk/gFf4Fv4YXhHjld3A9mWUnswuWZuLY95zje31iRyVn2ozHf9y4+c677/Xev/WB/+FHH3/y6e07n73QRaViOI0LXqhXEdXAmYRTwwyHV6UCKiIOL6PlN27+5RtQmhVyblYlLATNJEtZTA0Oze7P7r++vTcejteNXO1MNp09b9NOXt/p3Q2TIq4ESBNzqvXZZFyahaXKsJhD44eVhpLGS5rBGXYlFaAXdr3WhvRxJCFpofAnDVmP+tsQ5FF01WGxhkYVp6rujkZFscQZ3fh+V9OkRwvLZFkZkHErmVacmIK4EpCEKYgNX5GurmHLt4FkMaSKxgEVWlCTByVz6wzM8u0gU7TMA0GXEAPnl0Ptqhycs0hRtXIpFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaqn/i3UowFCcXFeOg7HzKjXwAySNVZDcOxrfizjqbkeYHDIFIBu7friY85wZ2ImJeAWNdf9bEX6f5MaU+uvRyEA91Aa5oY5zKjMYxoUY/VSBdl7So8lXB8f7xyMNgqHlInSYGJwzkw9cEgMmBxEaE9Q67uHhXvvwQ1dQisZ19fHDjBcR5SG+hg42BakrBdOk4GiAKdo2LhJ4FCrgtL7AFrj4ronO5pOFdRvnDNDZ5ZP5jEpXXAUSzjEBQWViw5QKxlcJpLTiprGhTi/6XZPo1Lmi8fvbYhp3EJJH4+FxEAuGomgLjpZHAVPr1FF0k0TuUJraUU1bsNUPzvBbO1g0u0k9BvzIFMxWIir4E0zJtiy6sd89f9ZY6SQEa6xoLMPlhjMw1wXjQLILiTaQjYYDzKoIt9NUbkuvF9hVmD157kpyITCfdMpno7qxml+KuOAWbZ9ipKsB5WVOm8ul/vh0p+pJxoHF+aCt/XUzuNEaj5fu+SAczfYuixnLBCqFrascnQ0jYcN2vLliC/EMj9LkOsRmoulKPAjriKozNF+YR0Vtwzfuv++Huao4kBxYlhs8XQ8PSkP6ZJ4DobGpKCcI88MlnhDj4f4B1H1y0frkMV4DVMZAIjDn+P26WIJiRK/L6LdSfZ+QNcFgPJyA6F+gZ3mhsDpMZqSQBE1FOKSGaJaAQ2zltTdp/iXBC+Dh/5KodSZrlsZVAa+Rye6lcbXzYn84weV9v783PdpcKLe8z70vvC+9iXfoTb1vvRPv1Iu9zPvZ+8X7tfdb7/fen72/2tCbNzaYu16n9f7+BwqfheM=</latexit><latexit sha1_base64="wtJ1SkLACwJOcMcL9/jLEzSB0Ao=">AAAHLHicfVVdj9w0FE0LDCV8tfSRF5ftSKjKfG217C5SpZGoKiq1YmFm20qbUXGSm8Qa2wm2083Uyk/gFf4Fv4YXhHjld3A9mWUnswuWZuLY95zje31iRyVn2ozHf9y4+c677/Xev/WB/+FHH3/y6e07n73QRaViOI0LXqhXEdXAmYRTwwyHV6UCKiIOL6PlN27+5RtQmhVyblYlLATNJEtZTA0Oze7P7r++vTcejteNXO1MNp09b9NOXt/p3Q2TIq4ESBNzqvXZZFyahaXKsJhD44eVhpLGS5rBGXYlFaAXdr3WhvRxJCFpofAnDVmP+tsQ5FF01WGxhkYVp6rujkZFscQZ3fh+V9OkRwvLZFkZkHErmVacmIK4EpCEKYgNX5GurmHLt4FkMaSKxgEVWlCTByVz6wzM8u0gU7TMA0GXEAPnl0Ptqhycs0hRtXIpFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaqn/i3UowFCcXFeOg7HzKjXwAySNVZDcOxrfizjqbkeYHDIFIBu7friY85wZ2ImJeAWNdf9bEX6f5MaU+uvRyEA91Aa5oY5zKjMYxoUY/VSBdl7So8lXB8f7xyMNgqHlInSYGJwzkw9cEgMmBxEaE9Q67uHhXvvwQ1dQisZ19fHDjBcR5SG+hg42BakrBdOk4GiAKdo2LhJ4FCrgtL7AFrj4ronO5pOFdRvnDNDZ5ZP5jEpXXAUSzjEBQWViw5QKxlcJpLTiprGhTi/6XZPo1Lmi8fvbYhp3EJJH4+FxEAuGomgLjpZHAVPr1FF0k0TuUJraUU1bsNUPzvBbO1g0u0k9BvzIFMxWIir4E0zJtiy6sd89f9ZY6SQEa6xoLMPlhjMw1wXjQLILiTaQjYYDzKoIt9NUbkuvF9hVmD157kpyITCfdMpno7qxml+KuOAWbZ9ipKsB5WVOm8ul/vh0p+pJxoHF+aCt/XUzuNEaj5fu+SAczfYuixnLBCqFrascnQ0jYcN2vLliC/EMj9LkOsRmoulKPAjriKozNF+YR0Vtwzfuv++Huao4kBxYlhs8XQ8PSkP6ZJ4DobGpKCcI88MlnhDj4f4B1H1y0frkMV4DVMZAIjDn+P26WIJiRK/L6LdSfZ+QNcFgPJyA6F+gZ3mhsDpMZqSQBE1FOKSGaJaAQ2zltTdp/iXBC+Dh/5KodSZrlsZVAa+Rye6lcbXzYn84weV9v783PdpcKLe8z70vvC+9iXfoTb1vvRPv1Iu9zPvZ+8X7tfdb7/fen72/2tCbNzaYu16n9f7+BwqfheM=</latexit><latexit sha1_base64="wtJ1SkLACwJOcMcL9/jLEzSB0Ao=">AAAHLHicfVVdj9w0FE0LDCV8tfSRF5ftSKjKfG217C5SpZGoKiq1YmFm20qbUXGSm8Qa2wm2083Uyk/gFf4Fv4YXhHjld3A9mWUnswuWZuLY95zje31iRyVn2ozHf9y4+c677/Xev/WB/+FHH3/y6e07n73QRaViOI0LXqhXEdXAmYRTwwyHV6UCKiIOL6PlN27+5RtQmhVyblYlLATNJEtZTA0Oze7P7r++vTcejteNXO1MNp09b9NOXt/p3Q2TIq4ESBNzqvXZZFyahaXKsJhD44eVhpLGS5rBGXYlFaAXdr3WhvRxJCFpofAnDVmP+tsQ5FF01WGxhkYVp6rujkZFscQZ3fh+V9OkRwvLZFkZkHErmVacmIK4EpCEKYgNX5GurmHLt4FkMaSKxgEVWlCTByVz6wzM8u0gU7TMA0GXEAPnl0Ptqhycs0hRtXIpFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaqn/i3UowFCcXFeOg7HzKjXwAySNVZDcOxrfizjqbkeYHDIFIBu7friY85wZ2ImJeAWNdf9bEX6f5MaU+uvRyEA91Aa5oY5zKjMYxoUY/VSBdl7So8lXB8f7xyMNgqHlInSYGJwzkw9cEgMmBxEaE9Q67uHhXvvwQ1dQisZ19fHDjBcR5SG+hg42BakrBdOk4GiAKdo2LhJ4FCrgtL7AFrj4ronO5pOFdRvnDNDZ5ZP5jEpXXAUSzjEBQWViw5QKxlcJpLTiprGhTi/6XZPo1Lmi8fvbYhp3EJJH4+FxEAuGomgLjpZHAVPr1FF0k0TuUJraUU1bsNUPzvBbO1g0u0k9BvzIFMxWIir4E0zJtiy6sd89f9ZY6SQEa6xoLMPlhjMw1wXjQLILiTaQjYYDzKoIt9NUbkuvF9hVmD157kpyITCfdMpno7qxml+KuOAWbZ9ipKsB5WVOm8ul/vh0p+pJxoHF+aCt/XUzuNEaj5fu+SAczfYuixnLBCqFrascnQ0jYcN2vLliC/EMj9LkOsRmoulKPAjriKozNF+YR0Vtwzfuv++Huao4kBxYlhs8XQ8PSkP6ZJ4DobGpKCcI88MlnhDj4f4B1H1y0frkMV4DVMZAIjDn+P26WIJiRK/L6LdSfZ+QNcFgPJyA6F+gZ3mhsDpMZqSQBE1FOKSGaJaAQ2zltTdp/iXBC+Dh/5KodSZrlsZVAa+Rye6lcbXzYn84weV9v783PdpcKLe8z70vvC+9iXfoTb1vvRPv1Iu9zPvZ+8X7tfdb7/fen72/2tCbNzaYu16n9f7+BwqfheM=</latexit><latexit sha1_base64="wtJ1SkLACwJOcMcL9/jLEzSB0Ao=">AAAHLHicfVVdj9w0FE0LDCV8tfSRF5ftSKjKfG217C5SpZGoKiq1YmFm20qbUXGSm8Qa2wm2083Uyk/gFf4Fv4YXhHjld3A9mWUnswuWZuLY95zje31iRyVn2ozHf9y4+c677/Xev/WB/+FHH3/y6e07n73QRaViOI0LXqhXEdXAmYRTwwyHV6UCKiIOL6PlN27+5RtQmhVyblYlLATNJEtZTA0Oze7P7r++vTcejteNXO1MNp09b9NOXt/p3Q2TIq4ESBNzqvXZZFyahaXKsJhD44eVhpLGS5rBGXYlFaAXdr3WhvRxJCFpofAnDVmP+tsQ5FF01WGxhkYVp6rujkZFscQZ3fh+V9OkRwvLZFkZkHErmVacmIK4EpCEKYgNX5GurmHLt4FkMaSKxgEVWlCTByVz6wzM8u0gU7TMA0GXEAPnl0Ptqhycs0hRtXIpFOc6iJA5U0UlEx2U1BhQUiPeKFYHOqcl6CBlJogpj9174jAlL4ygaqn/i3UowFCcXFeOg7HzKjXwAySNVZDcOxrfizjqbkeYHDIFIBu7friY85wZ2ImJeAWNdf9bEX6f5MaU+uvRyEA91Aa5oY5zKjMYxoUY/VSBdl7So8lXB8f7xyMNgqHlInSYGJwzkw9cEgMmBxEaE9Q67uHhXvvwQ1dQisZ19fHDjBcR5SG+hg42BakrBdOk4GiAKdo2LhJ4FCrgtL7AFrj4ronO5pOFdRvnDNDZ5ZP5jEpXXAUSzjEBQWViw5QKxlcJpLTiprGhTi/6XZPo1Lmi8fvbYhp3EJJH4+FxEAuGomgLjpZHAVPr1FF0k0TuUJraUU1bsNUPzvBbO1g0u0k9BvzIFMxWIir4E0zJtiy6sd89f9ZY6SQEa6xoLMPlhjMw1wXjQLILiTaQjYYDzKoIt9NUbkuvF9hVmD157kpyITCfdMpno7qxml+KuOAWbZ9ipKsB5WVOm8ul/vh0p+pJxoHF+aCt/XUzuNEaj5fu+SAczfYuixnLBCqFrascnQ0jYcN2vLliC/EMj9LkOsRmoulKPAjriKozNF+YR0Vtwzfuv++Huao4kBxYlhs8XQ8PSkP6ZJ4DobGpKCcI88MlnhDj4f4B1H1y0frkMV4DVMZAIjDn+P26WIJiRK/L6LdSfZ+QNcFgPJyA6F+gZ3mhsDpMZqSQBE1FOKSGaJaAQ2zltTdp/iXBC+Dh/5KodSZrlsZVAa+Rye6lcbXzYn84weV9v783PdpcKLe8z70vvC+9iXfoTb1vvRPv1Iu9zPvZ+8X7tfdb7/fen72/2tCbNzaYu16n9f7+BwqfheM=</latexit>
cutH(S) = f (2) + f (1)<latexit sha1_base64="JdV0NHpso/GwwYvqd/CeIvys+E4=">AAAHdnicfVVtb9s2EFa7Lem0t3T9OGBgFxhLUtuxU2RJBgQwsKJosRbLZqctYBkZJZ0kwiSlklRjl9CP2q8Z9m37F/u4o+UslpNNgC3qeM89vLuHZFhwpk2v98edux98+NHG5r2P/U8+/ezzL7buf/lK56WK4DzKea7ehFQDZxLODTMc3hQKqAg5vA6nP7j51+9AaZbLkZkXMBE0lSxhETVoutj6MQghZdLC23Jh2av8wMDM2Kg01YUNBDVZRLl9VlU7w11ySpKdg13yCF/9XT8AGa8gL7a2e93e4iE3B/3lYNtbPmcX9zceBHEelQKkiTjVetzvFWZiqTIs4oBLKTUUNJrSFMY4lFSAnthF1hVpoSUmSa7wJw1ZWP1VCMZRdN6IYg0NS07VrGkN83yKM7ry/SanSY4nlsmiNCCjmjIpOTE5ccUkMVMQGT4nTV7Dpu/bkkWQKBq1qdCuiu2CuXW2zfR9J1W0yNqCTiECzq9N9aocnLNQUTV3KeSXuh1i5FTlpYx1u6DGgJIa8UaxWVtntADdTphpY6ci9x07TMFzI6ia6v+K2hVgKE4uKsfB2FGZGPgF4soqiB8e9x6GHHlXPUwGqQKQlV28nM9lxgys+YS8hMq6/xUPv0UyYwr9/f4+KqyrDcaGWZRRmUI3ysX+2xK0U5Le7393eHJwsq9BMBRviPoSnUtmso5LosNkJ0SJg1r4PT7arl9+4ApKcQu4+vhByvOQ8gA/AwcbgNSlgkGccxTAADdAlMdwGijgdHaFzXHxTRGNR/2JdY1zAmh0+Ww0pNIVV4GES0xAUNwOQUIF4/MYElpyU9lAJ1fjpkh04lRR+a1VMo0dhPi01z1pR4IhKcqCo+SRwMx04kI0k8TYgTQzF2pQg63eG+NeO5xU60k9AdxkCoZzEeb8KaZk6yi6sj+9fFFZ6SgEq6yoLMPlBkMwtzmjIV6HhEvIksMBhmWI7TSla+ntBOsMw6cvXUmuCEb9RvlsOKus5tckzrlG2+dVfVRRXmS0ul7qr8/Xqh6nHFiUdera3zaDjdZ4vDTPB+HCrHZZDFkqkCmoVeXC2SAUNqjt1Q1ZiBd4KMe3IZYTVZNiL5iFVI1RfEEW5jMbvHP/LT/IVMmBZMDSzODpenRYGNIiowwIjUxJOUGYH0zxhOh1Dw5h1iJXT4s8wQuFyghICOYS96/zJUhG9KKMfk3V8glZBOj0un0QrSv0MMsVVofJlOSSoKgIh8QQzWJwiJW8tvvVv0HwAnj8v0HUIpNFlMpVAa+R/vqlcXPw6qDbx+X9fLA9OF5eKPe8r7xvvB2v7x15A++Zd+ade5H3m/e796f318bfm19vtja/rV3v3lliHniNZ7P3DzhnnvQ=</latexit><latexit sha1_base64="JdV0NHpso/GwwYvqd/CeIvys+E4=">AAAHdnicfVVtb9s2EFa7Lem0t3T9OGBgFxhLUtuxU2RJBgQwsKJosRbLZqctYBkZJZ0kwiSlklRjl9CP2q8Z9m37F/u4o+UslpNNgC3qeM89vLuHZFhwpk2v98edux98+NHG5r2P/U8+/ezzL7buf/lK56WK4DzKea7ehFQDZxLODTMc3hQKqAg5vA6nP7j51+9AaZbLkZkXMBE0lSxhETVoutj6MQghZdLC23Jh2av8wMDM2Kg01YUNBDVZRLl9VlU7w11ySpKdg13yCF/9XT8AGa8gL7a2e93e4iE3B/3lYNtbPmcX9zceBHEelQKkiTjVetzvFWZiqTIs4oBLKTUUNJrSFMY4lFSAnthF1hVpoSUmSa7wJw1ZWP1VCMZRdN6IYg0NS07VrGkN83yKM7ry/SanSY4nlsmiNCCjmjIpOTE5ccUkMVMQGT4nTV7Dpu/bkkWQKBq1qdCuiu2CuXW2zfR9J1W0yNqCTiECzq9N9aocnLNQUTV3KeSXuh1i5FTlpYx1u6DGgJIa8UaxWVtntADdTphpY6ci9x07TMFzI6ia6v+K2hVgKE4uKsfB2FGZGPgF4soqiB8e9x6GHHlXPUwGqQKQlV28nM9lxgys+YS8hMq6/xUPv0UyYwr9/f4+KqyrDcaGWZRRmUI3ysX+2xK0U5Le7393eHJwsq9BMBRviPoSnUtmso5LosNkJ0SJg1r4PT7arl9+4ApKcQu4+vhByvOQ8gA/AwcbgNSlgkGccxTAADdAlMdwGijgdHaFzXHxTRGNR/2JdY1zAmh0+Ww0pNIVV4GES0xAUNwOQUIF4/MYElpyU9lAJ1fjpkh04lRR+a1VMo0dhPi01z1pR4IhKcqCo+SRwMx04kI0k8TYgTQzF2pQg63eG+NeO5xU60k9AdxkCoZzEeb8KaZk6yi6sj+9fFFZ6SgEq6yoLMPlBkMwtzmjIV6HhEvIksMBhmWI7TSla+ntBOsMw6cvXUmuCEb9RvlsOKus5tckzrlG2+dVfVRRXmS0ul7qr8/Xqh6nHFiUdera3zaDjdZ4vDTPB+HCrHZZDFkqkCmoVeXC2SAUNqjt1Q1ZiBd4KMe3IZYTVZNiL5iFVI1RfEEW5jMbvHP/LT/IVMmBZMDSzODpenRYGNIiowwIjUxJOUGYH0zxhOh1Dw5h1iJXT4s8wQuFyghICOYS96/zJUhG9KKMfk3V8glZBOj0un0QrSv0MMsVVofJlOSSoKgIh8QQzWJwiJW8tvvVv0HwAnj8v0HUIpNFlMpVAa+R/vqlcXPw6qDbx+X9fLA9OF5eKPe8r7xvvB2v7x15A++Zd+ade5H3m/e796f318bfm19vtja/rV3v3lliHniNZ7P3DzhnnvQ=</latexit><latexit sha1_base64="JdV0NHpso/GwwYvqd/CeIvys+E4=">AAAHdnicfVVtb9s2EFa7Lem0t3T9OGBgFxhLUtuxU2RJBgQwsKJosRbLZqctYBkZJZ0kwiSlklRjl9CP2q8Z9m37F/u4o+UslpNNgC3qeM89vLuHZFhwpk2v98edux98+NHG5r2P/U8+/ezzL7buf/lK56WK4DzKea7ehFQDZxLODTMc3hQKqAg5vA6nP7j51+9AaZbLkZkXMBE0lSxhETVoutj6MQghZdLC23Jh2av8wMDM2Kg01YUNBDVZRLl9VlU7w11ySpKdg13yCF/9XT8AGa8gL7a2e93e4iE3B/3lYNtbPmcX9zceBHEelQKkiTjVetzvFWZiqTIs4oBLKTUUNJrSFMY4lFSAnthF1hVpoSUmSa7wJw1ZWP1VCMZRdN6IYg0NS07VrGkN83yKM7ry/SanSY4nlsmiNCCjmjIpOTE5ccUkMVMQGT4nTV7Dpu/bkkWQKBq1qdCuiu2CuXW2zfR9J1W0yNqCTiECzq9N9aocnLNQUTV3KeSXuh1i5FTlpYx1u6DGgJIa8UaxWVtntADdTphpY6ci9x07TMFzI6ia6v+K2hVgKE4uKsfB2FGZGPgF4soqiB8e9x6GHHlXPUwGqQKQlV28nM9lxgys+YS8hMq6/xUPv0UyYwr9/f4+KqyrDcaGWZRRmUI3ysX+2xK0U5Le7393eHJwsq9BMBRviPoSnUtmso5LosNkJ0SJg1r4PT7arl9+4ApKcQu4+vhByvOQ8gA/AwcbgNSlgkGccxTAADdAlMdwGijgdHaFzXHxTRGNR/2JdY1zAmh0+Ww0pNIVV4GES0xAUNwOQUIF4/MYElpyU9lAJ1fjpkh04lRR+a1VMo0dhPi01z1pR4IhKcqCo+SRwMx04kI0k8TYgTQzF2pQg63eG+NeO5xU60k9AdxkCoZzEeb8KaZk6yi6sj+9fFFZ6SgEq6yoLMPlBkMwtzmjIV6HhEvIksMBhmWI7TSla+ntBOsMw6cvXUmuCEb9RvlsOKus5tckzrlG2+dVfVRRXmS0ul7qr8/Xqh6nHFiUdera3zaDjdZ4vDTPB+HCrHZZDFkqkCmoVeXC2SAUNqjt1Q1ZiBd4KMe3IZYTVZNiL5iFVI1RfEEW5jMbvHP/LT/IVMmBZMDSzODpenRYGNIiowwIjUxJOUGYH0zxhOh1Dw5h1iJXT4s8wQuFyghICOYS96/zJUhG9KKMfk3V8glZBOj0un0QrSv0MMsVVofJlOSSoKgIh8QQzWJwiJW8tvvVv0HwAnj8v0HUIpNFlMpVAa+R/vqlcXPw6qDbx+X9fLA9OF5eKPe8r7xvvB2v7x15A++Zd+ade5H3m/e796f318bfm19vtja/rV3v3lliHniNZ7P3DzhnnvQ=</latexit><latexit sha1_base64="JdV0NHpso/GwwYvqd/CeIvys+E4=">AAAHdnicfVVtb9s2EFa7Lem0t3T9OGBgFxhLUtuxU2RJBgQwsKJosRbLZqctYBkZJZ0kwiSlklRjl9CP2q8Z9m37F/u4o+UslpNNgC3qeM89vLuHZFhwpk2v98edux98+NHG5r2P/U8+/ezzL7buf/lK56WK4DzKea7ehFQDZxLODTMc3hQKqAg5vA6nP7j51+9AaZbLkZkXMBE0lSxhETVoutj6MQghZdLC23Jh2av8wMDM2Kg01YUNBDVZRLl9VlU7w11ySpKdg13yCF/9XT8AGa8gL7a2e93e4iE3B/3lYNtbPmcX9zceBHEelQKkiTjVetzvFWZiqTIs4oBLKTUUNJrSFMY4lFSAnthF1hVpoSUmSa7wJw1ZWP1VCMZRdN6IYg0NS07VrGkN83yKM7ry/SanSY4nlsmiNCCjmjIpOTE5ccUkMVMQGT4nTV7Dpu/bkkWQKBq1qdCuiu2CuXW2zfR9J1W0yNqCTiECzq9N9aocnLNQUTV3KeSXuh1i5FTlpYx1u6DGgJIa8UaxWVtntADdTphpY6ci9x07TMFzI6ia6v+K2hVgKE4uKsfB2FGZGPgF4soqiB8e9x6GHHlXPUwGqQKQlV28nM9lxgys+YS8hMq6/xUPv0UyYwr9/f4+KqyrDcaGWZRRmUI3ysX+2xK0U5Le7393eHJwsq9BMBRviPoSnUtmso5LosNkJ0SJg1r4PT7arl9+4ApKcQu4+vhByvOQ8gA/AwcbgNSlgkGccxTAADdAlMdwGijgdHaFzXHxTRGNR/2JdY1zAmh0+Ww0pNIVV4GES0xAUNwOQUIF4/MYElpyU9lAJ1fjpkh04lRR+a1VMo0dhPi01z1pR4IhKcqCo+SRwMx04kI0k8TYgTQzF2pQg63eG+NeO5xU60k9AdxkCoZzEeb8KaZk6yi6sj+9fFFZ6SgEq6yoLMPlBkMwtzmjIV6HhEvIksMBhmWI7TSla+ntBOsMw6cvXUmuCEb9RvlsOKus5tckzrlG2+dVfVRRXmS0ul7qr8/Xqh6nHFiUdera3zaDjdZ4vDTPB+HCrHZZDFkqkCmoVeXC2SAUNqjt1Q1ZiBd4KMe3IZYTVZNiL5iFVI1RfEEW5jMbvHP/LT/IVMmBZMDSzODpenRYGNIiowwIjUxJOUGYH0zxhOh1Dw5h1iJXT4s8wQuFyghICOYS96/zJUhG9KKMfk3V8glZBOj0un0QrSv0MMsVVofJlOSSoKgIh8QQzWJwiJW8tvvVv0HwAnj8v0HUIpNFlMpVAa+R/vqlcXPw6qDbx+X9fLA9OF5eKPe8r7xvvB2v7x15A++Zd+ade5H3m/e796f318bfm19vtja/rV3v3lliHniNZ7P3DzhnnvQ=</latexit>
Submodularity is key to efficient algorithms.
What happens when the splitting function isn’t submodular?
Can we use some other algorithm?
<latexit sha1_base64="vCSQ5hxLftoc4zdzUNdXcsthqGM=">AAAIS3icfVXdbts2FLa7Ncm8v2a73A27wEMSyI6dIksyIEC6FsUKtFs2J20B08go6UgiTFIqScX2CD3FbrdH2gPsOXY37GKHtrPYTlYBtijyfN/55wkLwY3tdP6s33vv/ftr6xsfND786ONPPn2w+dkrk5c6gosoF7l+EzIDgiu4sNwKeFNoYDIU8DocPvHnr69AG56rczspYCBZqnjCI2Zx63KzvkZDSLlyTPBU7VYNamFs3fe5ailIUeiK20lFvqKZKVgErtPeP4hkRejV6BK2H+8QmsJb0mkTShegBk23BAlzzVWKcLKKnxPADjmZLynIwk4MWL+1SPik9e27DDghyTaVXG1TgY5a8phQ7RcBudkIWTQ0gpmMwPx0Z6fdoKDia78vH2x12p3pQ24vuvPFVm3+nF1urgU0zqNSgrIRUpt+t1PYgWPa8kgABrI0gBYPWQp9XComwQzcNGMVaeJOTJJc409ZMt1tLEKQR7PJEouzLCwF0+Pl3TDPh3hiqiV83xeEUaUMQUMc6FJAjMaJFDNiM7kPK+KlTY4GjquitKCimYFJKYjNiS8bEnMNkRUTsmyl5cNfAsUjSDSLAiaNZDYLCu69CiQbQgRCzOz1ooKHmumJdy4fmcCnJdV5qWITFMxa0Mogymo+DkzGCjBBwm0QMRH579hjCpFbyfTQ/B9rW4JleDiNqQDrzsvEwk8QVw4j8fCo8zAUqHdRwmaQagBVuenLy4wybmFFJhQlVM7/L0g0miSztjDf7O1htbaNRW4YRxlTKbSjXO69LcH4XjN73a8PjveP9wxIjiUYYnPJ1giz0fJOtLhqhdi4oKdyjw63Zq8G9WFk2Ng+Pg2aijxkguIn9bBTUKbUcBrnAkvjFNs6ymM4oRoEG19jczR+ubz6592B80nyyV7K6Nl5jykfXA0KRuiAZNglNGGSi0kMCSuFrRw1yfV6uSBM4iugajQXlRnMIMQnnfZxEGGnWow2E9gMqMCOTeIplp1Ebqrs2FOdzsDO7PaxCw8G1apTTwHbT0NvIsNcPEOX3IzFVO6Hly8qp7wKySsnK8fRXNoDe5cwbsSrkHAOmevwgF4ZYjpt6VN6t4JVDb1nL31IrhWcd5fC58Jx5Yy4UeKFZ2j3HCV9DJgoMlbdmPrz85Wox6kAHmWtWezvOsFEG7x4lm8O6WkWsyx7PJWoic6qytM5GkpHZ/vVrbKQL3DUxHch5gfVsopdOg6Z7mPx0SzMx45e+f9mg2b+hiIZ8DSzeO8eHhSWNMl5BoRFtmSCIKxBh3hD+AEA4ya5fprkKY5JpiIgIdgR9q+XJaiMmGkYGzNVzQYOHU/Q6rS7IJvX6F6Wa4wOzimSK4JFRQQklhgeg0cs+LXVrf4jwdHw6J0keurJlAWD4OdLd3Wa3F682m93D9qdH/e3To/mk2aj9kXty9p2rVs7rJ3Wvqud1S5qUV3Wf63/Vv99/Y/1v9b/Xv9nJnqvPsd8Xlt6Nu7/C+Rx6YI=</latexit>
Non-negativity we(A) 0.
Non-split ignoring we(e) = we(;) = 0.
C-B we(A) = f (min(|A|, |Ae|)).](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-36-320.jpg)
![37
Unlike graph min s-t cut,
hypergraph min s-t cut can be NP-hard.
w1 = 1
0 1 2 w2
??
Reducible/Submodular
NP-hard
Unknown
Hard Reducible
w3
3
2.5
2
1.5
1
0.5 1 1.5 2 2.5 w2
0.5
w2
w3
w4
4
3
2
1
0
1
1.5
2
2.5
1
2
3
max hyperedge size 4 or 5 max hyperedge size 6 or 7 max hyperedge size 8 or 9
Theorem [Veldt-Benson-Kleinberg 20a]. For C-B splitting functions,
Open Question: For 4-uniform hypergraphs, is there an efficient algorithm
to find the minimum s-t cut with no 2-2 splits (w1 = 1, w2 = ∞).
s
t
cutH(S) = f (2) + f (1)
= w2 + 1<latexit sha1_base64="buuvN8Zq181Nh/WWQIuguiXmNlg=">AAAHZHicfVXhbts2EFa7Lem0bksX7NeAgV3gIelsx0qXJRkQwMCKogVaLJudtkBoZJR0sgiTkkZStV1Cz7Kn2d/t915gz7Gj5SyWk42ALep43328u09kWAiuTa/31527773/wcbmvQ/9j+5//MmnWw8+e6XzUkVwHuUiV29CpkHwDM4NNwLeFAqYDAW8Dic/uPXXb0FpnmdDMy9gJNk44wmPmEHT5dYJNTAzNipNdWmpZCaNmLDPqmp3sEe+PiXJ7sEe+QYfwR6h1FmmlwdoCPzLrZ1et7cY5OYkWE52vOU4u3ywsU3jPColZCYSTOuLoFeYkWXK8EhA5dNSQ8GiCRvDBU4zJkGP7CLHirTQEpMkV/jLDFlY/VUIxlFs3ohiDQtLwdSsaQ3zfIIruvL9JqdJjkeWZ0VpIItqyqQUxOTElY7EXEFkxJw0eQ2fvGtnPIJEsajNpHZVbBfc7bNtJu86Y8WKtC3ZBCIQ4tpU78rBBQ8VU3OXQj7V7RAjj1VeZrFuF8wYUJlGvFF81tYpK0C3E27a2KnIvccOU4jcSKYm+r+idiUYhouLygkwdlgmBn6GuLIK4ofHvYehQN5VD5PCWAFklV08nM805QbWfEJRQmXd/4qH3yKpMYX+fn8fFdbVBmPDLEpZNoZulMv9X0vQToN6P/ju8OTgZF+D5CjVEJUpO1Nu0o5LosOzToiCBrXwe3y0Uz986grKUPCuPj4dizxkguIrdbA+ZLpU0I9zgQLoo9yjPIZTqkCw2RU2x803RXQxDEbWNc4JoNHls+GAZa64CjKYYgKSZbGlCZNczGNIWClMZalOruZNkejEqaLyW6tkGjsI8Wmve9KOJEdSlIVAySOBmenEhWgmibFpZmYuVL8GW/3oAr+1w1G1ntQTwI9MwWAuw1w8xZRsHUVX9seXLyqbOQrJKysry3G7dADmNmc0xOuQcAlZcjjAoAyxnaZ0Lb2dYJ1h8PSlK8kVwTBolM+Gs8pqcU3inGu0fV7VRxUTRcqq663+8nyt6vFYAI/STl3721aw0RqPl+b5IF2Y1S7LAR9LZKK1qlw4S0NpaW2vbshCvsAjOL4NsVyomhSP6Cxk6gLFR9Mwn1n61v23fJqqUgBJgY9Tg6fr0WFhSIsMUyAsMiUTBGE+neAJ0eseHMKsRa5GizzB64NlEZAQzBS/X+dLkIzoRRn9mqrlE7II0Ol1A5CtK/QgzRVWh2djkmcERUUEJIZoHoNDrOS1E1T/BsEL4PH/BlGLTBZRKlcFvEaC9Uvj5uTVQTfA7f307U7/eHmh3PO+8L7ydr3AO/L63jPvzDv3Iu8373fvD+/Pjb83729ub35eu969s8Rse42x+eU/D2WUeQ==</latexit><latexit sha1_base64="buuvN8Zq181Nh/WWQIuguiXmNlg=">AAAHZHicfVXhbts2EFa7Lem0bksX7NeAgV3gIelsx0qXJRkQwMCKogVaLJudtkBoZJR0sgiTkkZStV1Cz7Kn2d/t915gz7Gj5SyWk42ALep43328u09kWAiuTa/31527773/wcbmvQ/9j+5//MmnWw8+e6XzUkVwHuUiV29CpkHwDM4NNwLeFAqYDAW8Dic/uPXXb0FpnmdDMy9gJNk44wmPmEHT5dYJNTAzNipNdWmpZCaNmLDPqmp3sEe+PiXJ7sEe+QYfwR6h1FmmlwdoCPzLrZ1et7cY5OYkWE52vOU4u3ywsU3jPColZCYSTOuLoFeYkWXK8EhA5dNSQ8GiCRvDBU4zJkGP7CLHirTQEpMkV/jLDFlY/VUIxlFs3ohiDQtLwdSsaQ3zfIIruvL9JqdJjkeWZ0VpIItqyqQUxOTElY7EXEFkxJw0eQ2fvGtnPIJEsajNpHZVbBfc7bNtJu86Y8WKtC3ZBCIQ4tpU78rBBQ8VU3OXQj7V7RAjj1VeZrFuF8wYUJlGvFF81tYpK0C3E27a2KnIvccOU4jcSKYm+r+idiUYhouLygkwdlgmBn6GuLIK4ofHvYehQN5VD5PCWAFklV08nM805QbWfEJRQmXd/4qH3yKpMYX+fn8fFdbVBmPDLEpZNoZulMv9X0vQToN6P/ju8OTgZF+D5CjVEJUpO1Nu0o5LosOzToiCBrXwe3y0Uz986grKUPCuPj4dizxkguIrdbA+ZLpU0I9zgQLoo9yjPIZTqkCw2RU2x803RXQxDEbWNc4JoNHls+GAZa64CjKYYgKSZbGlCZNczGNIWClMZalOruZNkejEqaLyW6tkGjsI8Wmve9KOJEdSlIVAySOBmenEhWgmibFpZmYuVL8GW/3oAr+1w1G1ntQTwI9MwWAuw1w8xZRsHUVX9seXLyqbOQrJKysry3G7dADmNmc0xOuQcAlZcjjAoAyxnaZ0Lb2dYJ1h8PSlK8kVwTBolM+Gs8pqcU3inGu0fV7VRxUTRcqq663+8nyt6vFYAI/STl3721aw0RqPl+b5IF2Y1S7LAR9LZKK1qlw4S0NpaW2vbshCvsAjOL4NsVyomhSP6Cxk6gLFR9Mwn1n61v23fJqqUgBJgY9Tg6fr0WFhSIsMUyAsMiUTBGE+neAJ0eseHMKsRa5GizzB64NlEZAQzBS/X+dLkIzoRRn9mqrlE7II0Ol1A5CtK/QgzRVWh2djkmcERUUEJIZoHoNDrOS1E1T/BsEL4PH/BlGLTBZRKlcFvEaC9Uvj5uTVQTfA7f307U7/eHmh3PO+8L7ydr3AO/L63jPvzDv3Iu8373fvD+/Pjb83729ub35eu969s8Rse42x+eU/D2WUeQ==</latexit><latexit sha1_base64="buuvN8Zq181Nh/WWQIuguiXmNlg=">AAAHZHicfVXhbts2EFa7Lem0bksX7NeAgV3gIelsx0qXJRkQwMCKogVaLJudtkBoZJR0sgiTkkZStV1Cz7Kn2d/t915gz7Gj5SyWk42ALep43328u09kWAiuTa/31527773/wcbmvQ/9j+5//MmnWw8+e6XzUkVwHuUiV29CpkHwDM4NNwLeFAqYDAW8Dic/uPXXb0FpnmdDMy9gJNk44wmPmEHT5dYJNTAzNipNdWmpZCaNmLDPqmp3sEe+PiXJ7sEe+QYfwR6h1FmmlwdoCPzLrZ1et7cY5OYkWE52vOU4u3ywsU3jPColZCYSTOuLoFeYkWXK8EhA5dNSQ8GiCRvDBU4zJkGP7CLHirTQEpMkV/jLDFlY/VUIxlFs3ohiDQtLwdSsaQ3zfIIruvL9JqdJjkeWZ0VpIItqyqQUxOTElY7EXEFkxJw0eQ2fvGtnPIJEsajNpHZVbBfc7bNtJu86Y8WKtC3ZBCIQ4tpU78rBBQ8VU3OXQj7V7RAjj1VeZrFuF8wYUJlGvFF81tYpK0C3E27a2KnIvccOU4jcSKYm+r+idiUYhouLygkwdlgmBn6GuLIK4ofHvYehQN5VD5PCWAFklV08nM805QbWfEJRQmXd/4qH3yKpMYX+fn8fFdbVBmPDLEpZNoZulMv9X0vQToN6P/ju8OTgZF+D5CjVEJUpO1Nu0o5LosOzToiCBrXwe3y0Uz986grKUPCuPj4dizxkguIrdbA+ZLpU0I9zgQLoo9yjPIZTqkCw2RU2x803RXQxDEbWNc4JoNHls+GAZa64CjKYYgKSZbGlCZNczGNIWClMZalOruZNkejEqaLyW6tkGjsI8Wmve9KOJEdSlIVAySOBmenEhWgmibFpZmYuVL8GW/3oAr+1w1G1ntQTwI9MwWAuw1w8xZRsHUVX9seXLyqbOQrJKysry3G7dADmNmc0xOuQcAlZcjjAoAyxnaZ0Lb2dYJ1h8PSlK8kVwTBolM+Gs8pqcU3inGu0fV7VRxUTRcqq663+8nyt6vFYAI/STl3721aw0RqPl+b5IF2Y1S7LAR9LZKK1qlw4S0NpaW2vbshCvsAjOL4NsVyomhSP6Cxk6gLFR9Mwn1n61v23fJqqUgBJgY9Tg6fr0WFhSIsMUyAsMiUTBGE+neAJ0eseHMKsRa5GizzB64NlEZAQzBS/X+dLkIzoRRn9mqrlE7II0Ol1A5CtK/QgzRVWh2djkmcERUUEJIZoHoNDrOS1E1T/BsEL4PH/BlGLTBZRKlcFvEaC9Uvj5uTVQTfA7f307U7/eHmh3PO+8L7ydr3AO/L63jPvzDv3Iu8373fvD+/Pjb83729ub35eu969s8Rse42x+eU/D2WUeQ==</latexit><latexit sha1_base64="buuvN8Zq181Nh/WWQIuguiXmNlg=">AAAHZHicfVXhbts2EFa7Lem0bksX7NeAgV3gIelsx0qXJRkQwMCKogVaLJudtkBoZJR0sgiTkkZStV1Cz7Kn2d/t915gz7Gj5SyWk42ALep43328u09kWAiuTa/31527773/wcbmvQ/9j+5//MmnWw8+e6XzUkVwHuUiV29CpkHwDM4NNwLeFAqYDAW8Dic/uPXXb0FpnmdDMy9gJNk44wmPmEHT5dYJNTAzNipNdWmpZCaNmLDPqmp3sEe+PiXJ7sEe+QYfwR6h1FmmlwdoCPzLrZ1et7cY5OYkWE52vOU4u3ywsU3jPColZCYSTOuLoFeYkWXK8EhA5dNSQ8GiCRvDBU4zJkGP7CLHirTQEpMkV/jLDFlY/VUIxlFs3ohiDQtLwdSsaQ3zfIIruvL9JqdJjkeWZ0VpIItqyqQUxOTElY7EXEFkxJw0eQ2fvGtnPIJEsajNpHZVbBfc7bNtJu86Y8WKtC3ZBCIQ4tpU78rBBQ8VU3OXQj7V7RAjj1VeZrFuF8wYUJlGvFF81tYpK0C3E27a2KnIvccOU4jcSKYm+r+idiUYhouLygkwdlgmBn6GuLIK4ofHvYehQN5VD5PCWAFklV08nM805QbWfEJRQmXd/4qH3yKpMYX+fn8fFdbVBmPDLEpZNoZulMv9X0vQToN6P/ju8OTgZF+D5CjVEJUpO1Nu0o5LosOzToiCBrXwe3y0Uz986grKUPCuPj4dizxkguIrdbA+ZLpU0I9zgQLoo9yjPIZTqkCw2RU2x803RXQxDEbWNc4JoNHls+GAZa64CjKYYgKSZbGlCZNczGNIWClMZalOruZNkejEqaLyW6tkGjsI8Wmve9KOJEdSlIVAySOBmenEhWgmibFpZmYuVL8GW/3oAr+1w1G1ntQTwI9MwWAuw1w8xZRsHUVX9seXLyqbOQrJKysry3G7dADmNmc0xOuQcAlZcjjAoAyxnaZ0Lb2dYJ1h8PSlK8kVwTBolM+Gs8pqcU3inGu0fV7VRxUTRcqq663+8nyt6vFYAI/STl3721aw0RqPl+b5IF2Y1S7LAR9LZKK1qlw4S0NpaW2vbshCvsAjOL4NsVyomhSP6Cxk6gLFR9Mwn1n61v23fJqqUgBJgY9Tg6fr0WFhSIsMUyAsMiUTBGE+neAJ0eseHMKsRa5GizzB64NlEZAQzBS/X+dLkIzoRRn9mqrlE7II0Ol1A5CtK/QgzRVWh2djkmcERUUEJIZoHoNDrOS1E1T/BsEL4PH/BlGLTBZRKlcFvEaC9Uvj5uTVQTfA7f307U7/eHmh3PO+8L7ydr3AO/L63jPvzDv3Iu8373fvD+/Pjb83729ub35eu969s8Rse42x+eU/D2WUeQ==</latexit>](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-37-320.jpg)


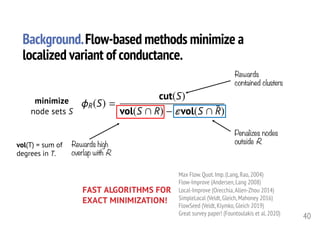
![s
t
2
4
4
7
3
4
7
3
2
1
3
2
6
4
5
7
8
9
10Set
R
4
1
3
2
6
4
5
7
8
9
10
s
t
2
4
4
7
3
4
7
3
2
1
3
2
6
4
5
7
8
9
10Set
R
4
[Andersen-Lang 08,Orecchia-Zhou 14,Veldt+ 16]
Construct G’
R(S) < ↵ () min s-t cut of G0
< ↵vol(R)
Compute min s-t cut of G’.
41
Connect R to a source node s ; edges weighted with respect to 𝛼.
Connect VR to a sink node t ; edges weighted with respect to β = 𝛼ε.
Is R(S) < ↵ for any S?
Background.Flow methods repeatedly solve min-cut
problems on an auxiliary graph.](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-41-320.jpg)
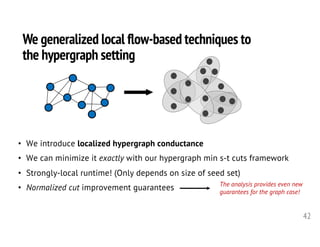
![43
We define hypergraph s-t cut problems similar to the
ones used in the graph case.
t
𝜀𝛼dj
r
j
s
𝛼dr
R
minimize
S⇢V
HLCR,"(S) =
cutH(S)
volH(S R) "volH(S ¯R)
cutH(S) = cut from C-B splitting function
volH(X) =
X
i2X
X
e2E
1 = sum of hypergraph deg
<latexit sha1_base64="1b3WAyFb1xHR0eMss1XSCe103wc=">AAAInXicfVVtb9s2EHayrfW0l7brx30Yu9RDW9iOnS5rsiJAsL6gBdIti9M2QGh4lHSyCJOSSlKJU4L/c/szw46S09hOMgK2+HL3POTD411YCK5Nr/fPyupnn39x42bzy+Crr7/59tbtO9+903mpIngb5SJXRyHTIHgGbw03Ao4KBUyGAt6Hk2d+/f0JKM3z7NCcFTCUbJzxhEfM4NTozsoHKnnGJf8IIzsgVJehBkPeOfqUPg2ogakJE/tq75kb2YM2PWEKCs1FnrkHg4fkpx0S0ESxyFaWNiqNG1HJTBoxYV95G2dJvXaSi6U1GrGCHDwkHTKHe601qcxpyJQ9cA8dofR4S8phcC2z392nRZKoXJJnnd+IRlmN4dmYJGUWeRUqrI0LrEvcRzWWLuXIckJ5Ro5cPYJq9MKRPjknw3mSJyRFsdVYsSIlMYwVgCZoef/ovhvdXut1e1Ujlzv9WWetMWv7ozs37tI4j0oJmYkE0/q43yvM0DJleCTABbTUULBowsZwjN2MSdBDWwWHIy2ciUmSK/xlhlSzwbwL4ih2toBiDQtLwdR0cTbM8wmuaBcEi5wm2RpanhWlgSyqKZNSEJMTH3Mk5goiI87IIq/hk4/tjEfgI6jNpPaStwvu99k2k4+dSr62ZBOIQIiLqXpX3l3wUDF15o+Qn+p2iMhjlZdZrNsFMwZUptHfKD5t65QVoNsJN2281siPY+9TiNxIpib6OtSuBMNwsVJOgLGHZWLgAGJnFcT3tnr3QoG88xYmra48c7b6eJvTlBtYsglFCc76/zmLoEVSYwr96/o6xlNXG8SGaZSybAzdKJfrH0rQPmz1ev+Xze2N7XUNkuMbD/FJy84pN2nHH6LDs06ImQBUZff4yVr9CagXlGGm8PoEdCzykAmKQ+rddiHTpYLdOBcYALuYJ6I8hh2qQLDpuW+Om18MouPD/tD6i/MBsHDL+4cDlnlxFWRwigeQLIstTZjk4iyGhJXCOEt1ct5fDBKd+KhwQWueTOMNQrzT6263I0xfBtVmAkMeCcxUJx5i8ZCITTMz9VC7tbPVj47xrW0O3fKhngM+MgWDMxnm4iUeydYo2tk/3uw5m3kKyZ2VznLcLh2AucoYJ+Jll3DmMuPwDgPMuJi4S3+lVxMsMwxevvGSnBMc9hfks+HUWS0uSLxx7W1fo6XXgIkiZe5iq3+9XlI9HgvgUdqptb9qBS9aY3pZzA/Sw8zfshzwsUQmWkeVh7M0lJbW8+5SWMg9rF3xVR6zBbdI8YhOsSIcY/DRNMynlp74/1ZAU1UKICnwcWowuz7ZLAxpkcMUCItMyQRBt4BOMEP0uhubMG2R89Yiz7HusiwCEoI5xffrbQmSEV3JGNRUrYCQCqDT6/ZBts69B2muUB1fYbCcYVARAYkhmsfgPebOtdZ3n0CwADz+XxBVnaRCcV4FLCP95aJxufNuo9vH7f3589ru1qygNBvfN35sPGj0G08au41Xjf3G20a08vfKv6s3V5vNH5ovmnvN32vT1ZWZz93GQmu+/w8XFAmq</latexit><latexit sha1_base64="1b3WAyFb1xHR0eMss1XSCe103wc=">AAAInXicfVVtb9s2EHayrfW0l7brx30Yu9RDW9iOnS5rsiJAsL6gBdIti9M2QGh4lHSyCJOSSlKJU4L/c/szw46S09hOMgK2+HL3POTD411YCK5Nr/fPyupnn39x42bzy+Crr7/59tbtO9+903mpIngb5SJXRyHTIHgGbw03Ao4KBUyGAt6Hk2d+/f0JKM3z7NCcFTCUbJzxhEfM4NTozsoHKnnGJf8IIzsgVJehBkPeOfqUPg2ogakJE/tq75kb2YM2PWEKCs1FnrkHg4fkpx0S0ESxyFaWNiqNG1HJTBoxYV95G2dJvXaSi6U1GrGCHDwkHTKHe601qcxpyJQ9cA8dofR4S8phcC2z392nRZKoXJJnnd+IRlmN4dmYJGUWeRUqrI0LrEvcRzWWLuXIckJ5Ro5cPYJq9MKRPjknw3mSJyRFsdVYsSIlMYwVgCZoef/ovhvdXut1e1Ujlzv9WWetMWv7ozs37tI4j0oJmYkE0/q43yvM0DJleCTABbTUULBowsZwjN2MSdBDWwWHIy2ciUmSK/xlhlSzwbwL4ih2toBiDQtLwdR0cTbM8wmuaBcEi5wm2RpanhWlgSyqKZNSEJMTH3Mk5goiI87IIq/hk4/tjEfgI6jNpPaStwvu99k2k4+dSr62ZBOIQIiLqXpX3l3wUDF15o+Qn+p2iMhjlZdZrNsFMwZUptHfKD5t65QVoNsJN2281siPY+9TiNxIpib6OtSuBMNwsVJOgLGHZWLgAGJnFcT3tnr3QoG88xYmra48c7b6eJvTlBtYsglFCc76/zmLoEVSYwr96/o6xlNXG8SGaZSybAzdKJfrH0rQPmz1ev+Xze2N7XUNkuMbD/FJy84pN2nHH6LDs06ImQBUZff4yVr9CagXlGGm8PoEdCzykAmKQ+rddiHTpYLdOBcYALuYJ6I8hh2qQLDpuW+Om18MouPD/tD6i/MBsHDL+4cDlnlxFWRwigeQLIstTZjk4iyGhJXCOEt1ct5fDBKd+KhwQWueTOMNQrzT6263I0xfBtVmAkMeCcxUJx5i8ZCITTMz9VC7tbPVj47xrW0O3fKhngM+MgWDMxnm4iUeydYo2tk/3uw5m3kKyZ2VznLcLh2AucoYJ+Jll3DmMuPwDgPMuJi4S3+lVxMsMwxevvGSnBMc9hfks+HUWS0uSLxx7W1fo6XXgIkiZe5iq3+9XlI9HgvgUdqptb9qBS9aY3pZzA/Sw8zfshzwsUQmWkeVh7M0lJbW8+5SWMg9rF3xVR6zBbdI8YhOsSIcY/DRNMynlp74/1ZAU1UKICnwcWowuz7ZLAxpkcMUCItMyQRBt4BOMEP0uhubMG2R89Yiz7HusiwCEoI5xffrbQmSEV3JGNRUrYCQCqDT6/ZBts69B2muUB1fYbCcYVARAYkhmsfgPebOtdZ3n0CwADz+XxBVnaRCcV4FLCP95aJxufNuo9vH7f3589ru1qygNBvfN35sPGj0G08au41Xjf3G20a08vfKv6s3V5vNH5ovmnvN32vT1ZWZz93GQmu+/w8XFAmq</latexit><latexit sha1_base64="1b3WAyFb1xHR0eMss1XSCe103wc=">AAAInXicfVVtb9s2EHayrfW0l7brx30Yu9RDW9iOnS5rsiJAsL6gBdIti9M2QGh4lHSyCJOSSlKJU4L/c/szw46S09hOMgK2+HL3POTD411YCK5Nr/fPyupnn39x42bzy+Crr7/59tbtO9+903mpIngb5SJXRyHTIHgGbw03Ao4KBUyGAt6Hk2d+/f0JKM3z7NCcFTCUbJzxhEfM4NTozsoHKnnGJf8IIzsgVJehBkPeOfqUPg2ogakJE/tq75kb2YM2PWEKCs1FnrkHg4fkpx0S0ESxyFaWNiqNG1HJTBoxYV95G2dJvXaSi6U1GrGCHDwkHTKHe601qcxpyJQ9cA8dofR4S8phcC2z392nRZKoXJJnnd+IRlmN4dmYJGUWeRUqrI0LrEvcRzWWLuXIckJ5Ro5cPYJq9MKRPjknw3mSJyRFsdVYsSIlMYwVgCZoef/ovhvdXut1e1Ujlzv9WWetMWv7ozs37tI4j0oJmYkE0/q43yvM0DJleCTABbTUULBowsZwjN2MSdBDWwWHIy2ciUmSK/xlhlSzwbwL4ih2toBiDQtLwdR0cTbM8wmuaBcEi5wm2RpanhWlgSyqKZNSEJMTH3Mk5goiI87IIq/hk4/tjEfgI6jNpPaStwvu99k2k4+dSr62ZBOIQIiLqXpX3l3wUDF15o+Qn+p2iMhjlZdZrNsFMwZUptHfKD5t65QVoNsJN2281siPY+9TiNxIpib6OtSuBMNwsVJOgLGHZWLgAGJnFcT3tnr3QoG88xYmra48c7b6eJvTlBtYsglFCc76/zmLoEVSYwr96/o6xlNXG8SGaZSybAzdKJfrH0rQPmz1ev+Xze2N7XUNkuMbD/FJy84pN2nHH6LDs06ImQBUZff4yVr9CagXlGGm8PoEdCzykAmKQ+rddiHTpYLdOBcYALuYJ6I8hh2qQLDpuW+Om18MouPD/tD6i/MBsHDL+4cDlnlxFWRwigeQLIstTZjk4iyGhJXCOEt1ct5fDBKd+KhwQWueTOMNQrzT6263I0xfBtVmAkMeCcxUJx5i8ZCITTMz9VC7tbPVj47xrW0O3fKhngM+MgWDMxnm4iUeydYo2tk/3uw5m3kKyZ2VznLcLh2AucoYJ+Jll3DmMuPwDgPMuJi4S3+lVxMsMwxevvGSnBMc9hfks+HUWS0uSLxx7W1fo6XXgIkiZe5iq3+9XlI9HgvgUdqptb9qBS9aY3pZzA/Sw8zfshzwsUQmWkeVh7M0lJbW8+5SWMg9rF3xVR6zBbdI8YhOsSIcY/DRNMynlp74/1ZAU1UKICnwcWowuz7ZLAxpkcMUCItMyQRBt4BOMEP0uhubMG2R89Yiz7HusiwCEoI5xffrbQmSEV3JGNRUrYCQCqDT6/ZBts69B2muUB1fYbCcYVARAYkhmsfgPebOtdZ3n0CwADz+XxBVnaRCcV4FLCP95aJxufNuo9vH7f3589ru1qygNBvfN35sPGj0G08au41Xjf3G20a08vfKv6s3V5vNH5ovmnvN32vT1ZWZz93GQmu+/w8XFAmq</latexit><latexit sha1_base64="1b3WAyFb1xHR0eMss1XSCe103wc=">AAAInXicfVVtb9s2EHayrfW0l7brx30Yu9RDW9iOnS5rsiJAsL6gBdIti9M2QGh4lHSyCJOSSlKJU4L/c/szw46S09hOMgK2+HL3POTD411YCK5Nr/fPyupnn39x42bzy+Crr7/59tbtO9+903mpIngb5SJXRyHTIHgGbw03Ao4KBUyGAt6Hk2d+/f0JKM3z7NCcFTCUbJzxhEfM4NTozsoHKnnGJf8IIzsgVJehBkPeOfqUPg2ogakJE/tq75kb2YM2PWEKCs1FnrkHg4fkpx0S0ESxyFaWNiqNG1HJTBoxYV95G2dJvXaSi6U1GrGCHDwkHTKHe601qcxpyJQ9cA8dofR4S8phcC2z392nRZKoXJJnnd+IRlmN4dmYJGUWeRUqrI0LrEvcRzWWLuXIckJ5Ro5cPYJq9MKRPjknw3mSJyRFsdVYsSIlMYwVgCZoef/ovhvdXut1e1Ujlzv9WWetMWv7ozs37tI4j0oJmYkE0/q43yvM0DJleCTABbTUULBowsZwjN2MSdBDWwWHIy2ciUmSK/xlhlSzwbwL4ih2toBiDQtLwdR0cTbM8wmuaBcEi5wm2RpanhWlgSyqKZNSEJMTH3Mk5goiI87IIq/hk4/tjEfgI6jNpPaStwvu99k2k4+dSr62ZBOIQIiLqXpX3l3wUDF15o+Qn+p2iMhjlZdZrNsFMwZUptHfKD5t65QVoNsJN2281siPY+9TiNxIpib6OtSuBMNwsVJOgLGHZWLgAGJnFcT3tnr3QoG88xYmra48c7b6eJvTlBtYsglFCc76/zmLoEVSYwr96/o6xlNXG8SGaZSybAzdKJfrH0rQPmz1ev+Xze2N7XUNkuMbD/FJy84pN2nHH6LDs06ImQBUZff4yVr9CagXlGGm8PoEdCzykAmKQ+rddiHTpYLdOBcYALuYJ6I8hh2qQLDpuW+Om18MouPD/tD6i/MBsHDL+4cDlnlxFWRwigeQLIstTZjk4iyGhJXCOEt1ct5fDBKd+KhwQWueTOMNQrzT6263I0xfBtVmAkMeCcxUJx5i8ZCITTMz9VC7tbPVj47xrW0O3fKhngM+MgWDMxnm4iUeydYo2tk/3uw5m3kKyZ2VznLcLh2AucoYJ+Jll3DmMuPwDgPMuJi4S3+lVxMsMwxevvGSnBMc9hfks+HUWS0uSLxx7W1fo6XXgIkiZe5iq3+9XlI9HgvgUdqptb9qBS9aY3pZzA/Sw8zfshzwsUQmWkeVh7M0lJbW8+5SWMg9rF3xVR6zBbdI8YhOsSIcY/DRNMynlp74/1ZAU1UKICnwcWowuz7ZLAxpkcMUCItMyQRBt4BOMEP0uhubMG2R89Yiz7HusiwCEoI5xffrbQmSEV3JGNRUrYCQCqDT6/ZBts69B2muUB1fYbCcYVARAYkhmsfgPebOtdZ3n0CwADz+XxBVnaRCcV4FLCP95aJxufNuo9vH7f3589ru1qygNBvfN35sPGj0G08au41Xjf3G20a08vfKv6s3V5vNH5ovmnvN32vT1ZWZz93GQmu+/w8XFAmq</latexit>
Hypergraph cut function
Encourage overlap with
reference set.
Discourage overlap
outside reference set
⟶
di = # hyperedges node r is in
volH(S) =
X
i2S
di
<latexit sha1_base64="E541uqeWvYyixS/NzXbACyuddlM=">AAAE73icjVNLbxMxEHZpgBJeLRy5bKkqFRSipIAoh0oVoKqVqCgkfUjdKHi9s4kV7wPb2ya1/Be4ckNcOXHhCv+Df8M4SWk27QFLuzs78803nleQCa50rfZn5sps6eq163M3yjdv3b5zd37h3r5Kc8lgj6UilYcBVSB4AnuaawGHmQQaBwIOgt5rZz84Bql4mjT1IINWTDsJjzijGlXt+RX/OBVtP6a6y6gwW3al8chb93yVx23DPZ8nXsN6YZu355dq1drweBeF+lhYIuOz216Y/eGHKctjSDQTVKmjei3TLUOl5kyALfu5goyyHu3AEYoJjUG1zDAl6y2jJvSiVOKTaG+onfRAGkkHtqiKlRrEATq7dNS0zSkvtWka5ILKfpEtSNMeWtTURXW01jI8yXINCRvdM8qFp1PPldcLuQSmxcArRuidPulImnVHZJr3TgUPJJUDl0d6oiqqSzNQFewBq0RcI26YsgBtmnmk4QOE1kgIF9dqi4FA2kmE7kJHAiTWDD8Oc9LlGqYwgcjBGveeREwk16y3jCu3y6xw/91mgyauEhISOGFpHNMkNH5EYy4GIUQ0F9oaX0VncsFbRcPSl5cnYylMFcL1WvVlhcUcY2J9BPYf+XVfRcgQ0x5QHGitAVuPzH6i+45pY+Rr1OMjnLvnrX/YFJNE6BvAeZPQwFlIxSbmY0Ykypp3O2+tSVyAmFsTWzMsdQP0ZWBUhNMuwdhlHMM5NPJA4eblbqH+K0Bjc8fV44y/WS+UzgR9a5Q4j+HAI2+zjUhXASqyLrXnN/24bctlf7I1LHcN0dDXQWTcjy3acevP7e4HCXDF69MLfVHYX63Wn1ZX3z9b2ng1XvY58oA8JCukTl6QDbJFdskeYeQz+Ul+kd+lT6Uvpa+lbyPolZmxz31SOKXvfwH7u76o</latexit>
Theorem [Veldt-Benson-Kleinberg 20b]. We can repeatedly solve min
hypergraph s-t cut problems with different 𝛼 to exactly minimize the
hypergraph localized conductance (HLC) exactly.](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-43-320.jpg)
![We carefully apply graph reduction techniques
to growing subsets of the hypergraph.
44
s
R
t
s
t
𝛼
Theorem [Veldt-Benson-Kleinberg 20b]. Strong locality.
Can make this algorithm run in time proportional to the
size of seed set (does not look at the full hypergraph).](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-44-320.jpg)
![<latexit sha1_base64="ff4QhRAHZfL2qp7+qW21R4vDGq8=">AAAIZXicfVXdbhtFFLYLtGahtAHEDRdMiS0lwXbsVCEJUiVLVBWRWhFqJ63kscLs7tndkWdmtzOzsc1qr3kabuFZeAJegzO2k9pOYKX1jmfOd86c7/z5meDGdjp/V+998OFH9x/UPvY++fThZ48eb31+YdJcB3AepCLVb31mQHAF55ZbAW8zDUz6At744x/d+Zsr0IanamBnGYwkixWPeMAsbl1uVQlVKVchKEtOI8KIZToGSwy+9QGhJvfd8qJODCJMxMF41IeYq4IJHqu90qORZkFBLUytHxVXqSh3EBiwjLzeLTf2d0tCY3hH7sBQn+liUN4NXB4i/DuC5i3zKKjw5gqDBBSp0yzhO/1dQsWNhS7qceJo1h0OdkmdTBLQQOr9OuGG2ATmvmqwuVYQEn9GkFvCRJxqbhPZvny83Wl35g+5veguF9uV5XN2uXW/ScM0yCVyGghmzLDbyeyoYNryQAASlhvIWDBmMQxxqZgEMyrmsSxJA3dCEqUaX4zJfNdbhaAezWZrWgrL/FwwPV3f9dN0jCemXMMPXaoYlUsfaQibOhcQ4uWu/T2ADfHcRsejgqsst6CCxQWjXBCbEpdQJOQaAitmZP2Wlo9/ayoegItDk0kjmU2aGXdeNSUbQwBCLO7rRAX3NdMz51w6MU0ftcQ6zVVomhmzFrQyiLKaT5smYRmYZsRtM2AicP9Dh8lEaiXTY/NfWtvSZYJH55wKsMUgjyy8hrAskIknx50nvkC7qxKYHrEGUGUx/ziZScItbMj4IoeycL8rEl6DJNZm5of9fUzltrGoG6ZBwlQM7SCV++9yMK4KzX73+8OTg5N9A5JjsfpYabI1wWi0nBMtrlo+ljToudzTo+3Fx6OORoYl7/jxaCxSnwlMfksdrAfK5Bp6YSowNXpY8EEawjOqQbDpNTbFy6+n13DQHRUuSC7YaxE9G/SZcuRqUDBBByTDEqQRk1zMQohYLiyWm4mu1+sJYSKXAaXXWDVmMIIQPuu0T5qB5Gg01kxgMaABOzWRU7HuJOqmyk6dqt4CXJi9IVbh4ajcdOo5YPlp6M+kn4oX6FKx0GLK4udXL8tCOROSl4UsC47XpX2wdwnjRrgJ8ZeQpQ0H6GOrxA6cu5DebWDTQv/FK0fJtYFBd42+wp+WhRHvjTjhBbo4RUnHARNZwsr3V/31dIP1MBbAg6S14P6uEwy0wcaz3jmkU7MaZdnnsURLdJFVTh12VlnQxX55Ky3kSxxC4V2I5UG5bmKPTrHHDzH5aOKn04Jeud+GRxPXoUgCPE4s9t2jw8ySBsGOT1hgcyYIwjw6xg7RaR8cwrRBrp8GeY4DlKkACM6ACdavkyVojJg5jd7CVMMjZK6g1Wl3QTau0f0k1cgOVzFJ1XxSCIhwNPIQHGLFr+1ueaMER8PT/1Wi557MtSAJJc6X7uY0ub24OGh3D9udXw62e8fLSVOrfF35trJT6VaOKr3KT5WzynklqP5e/aP6Z/WvB//UHta+rH21EL1XXWK+qKw9tW/+Ba2e9dU=</latexit>
If a target set T ⇢ V satisfies
vol(T R)
vol(T)
vol(¯T R)
vol(¯T)
+
Then (S) 1
(T) where S is the set returned by our algorithm.
45
We prove new normalized cut guarantees
that are new even for the graph case.
(S) =
cut(S)
vol(S)
+
cut(S)
vol(S)<latexit sha1_base64="+2zPfSQ7UOPKTHfrSfqqRxABg7w=">AAAFDXicjVNLbxMxEHbbACW8Wjhy2VJVaiFESQFRDpUqQBWVqCgkfUjdqHi9s4kV70O2t01q+TfwR5A4cUNcuXND8GMYJynNpj1gKdnxzDffPDwTZIIrXav9mpqeKV25em32evnGzVu378zN391TaS4Z7LJUpPIgoAoET2BXcy3gIJNA40DAftB95ez7xyAVT5Om7mfQimk74RFnVKPqaG7Tzzp8ubHirXt+JCkzPss13q3xj1PhBO/RpRY/RVoX1TTsij2aW6xVa4PjXRTqI2GRjM7O0fzMFz9MWR5DopmgSh3Wa5luGSo1ZwJs2c8VZJR1aRsOUUxoDKplBgVbbwk1oRelEn+J9gbacQ+kkbRvi6pYqX4coHNMdUdN2pzyUpumQS6o7BXZgjTtokVNJKqjtZbhSZZrSNgwzygXnk4913wv5BKYFn2vGKF7+rgtadYZkmnePRU8kFT2XR3piaqoDs1AVRgVrBJxjbhByQK0aeaRhg8QWiMhXFirLQQCaccRugNtCZBYM/g4zEmHa5jABCIHa9z/OGKsuGa9ZVy7XWWF/HeaDZq4TkhI4ISlcUyT0PgRjbnohxDRXGicGhWdyQVvFQ1aX14aj6WwVAjXa9UXFRZzjIn9Efj+yK97KkKGmHaB4rhrDfj0yOwnuueYNoa+Rj08xLl71vqHTbFIhL4GnDcJDZyFVGxiPWZIoqx5t/3WmsQFiLk1sTWDVjdAXwZGRTjpEoxcRjGcQyMPFO5l7tbtvwI0NrddP874m/VC60zQs0aJ8xgOPPQ2W4h0HaAi61B7nunHLVsu++NPg5uMWA09HUTGXWzRjgt+bncXJMAVr08u9EVhb7Vaf1Jdff90cePlaNlnyX3ygCyTOnlONsgbskN2CSOfyU/ym/wpfSp9LX0rfR9Cp6dGPvdI4ZR+/AUEuMqZ</latexit>
Normalized cut is another ratio-cut
objective related to conductance.
If T overlaps enough
with seed set R...
...then our output has normalized cut almost as good as T.
Theorem [Veldt-Benson-Kleinberg 20b]. Normalized cut improvement.](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-45-320.jpg)
![48
Gadget reductions sometimes create dense graphs,
which can make computations expensive.
Theorem [Veldt-Benson-Kleinberg 20c].Any submodular C-B splitting function can
be 𝜀-approx with log r / 𝜀 splitting functions (instead of r, r = hyperedge size).
And one specific case…
• r = 60k clique expansion only need O(r / √𝜀) instead of O(r2)
0 1 2 3
0
2
4
6
8
10
e0
1 e00
1
e0
2 e00
2
e0
3 e00
3
2 2
2 2
2 2
2 2
2 2
2 2
2 2
2 2
2 2
2 2
2 2
2 2
1 1
1 1
1 1
1 1
1 1
1 1
2
4
3
0 1 2 3
0
2
4
6
8
10
e0
e00
5 5
5 5
5 5
5 5
5 5
5 5
9](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-48-320.jpg)


![Background.Graph Laplacians,diffusions,and spectral
graph theory underly many graph data methods.
51
Low-dimensional embeddings
[Belkin-Niyogi 02; Coifman-Lafon 06]
Personalized PageRank
[Andersen-Chung-Lang 08; Gleich 15]
<latexit sha1_base64="QQhZuRTVdivo8Dt7YLhgdqyYsKI=">AAAHqHicfVVtb9s2EFa7rem8t3T7uC/sUg9DIDuWuyzNgAAGVhQr0G7Z7DQdrCAjpZNEmKQ0kmqUCfqD+wf7F/u6fdrRslvLzSbAFkXe8xzvuTuSFYIbOxr9eev2O+++d2fn7vu9Dz786ONPdu99+sLkpY7gLMpFrl8yakBwBWeWWwEvCw1UMgHnbPGdWz9/BdrwXM3sdQEXkqaKJzyiFqcud+MHP4QMUq5qJqnVvGqqy4B8SarLcQgqfj1LTsiWHQkFuonpZdAi1p9jhJIO9sHl7t5oOFo+5O1BsBrseavn9PLeHT+M86iUoGwkqDHzYFTYi5pqyyMBTS8sDRQ0WtAU5jhUVIK5qJdyNKSPMzFJco0/ZclytrcJQR5NrzsstaWsFFRX3VmW5wtcMU0HP3dqG1VKBhpiX5cCYtycSHPNbSbHsGVe2uTRRc1VUVpQUbvBpBTE5sTlhMRcQ2TFNenu0vLF777iESSaRj6VBvXM/IK7qHxJFxCBEO1+nangTFN97YLLr4zPkCXVeali4xfUWtDK+G1GfJPRAoyfcOtHVETuO3aYQuRWUr0w/8U6lGApLi41FWDrWZlY+BnipkYl7j8a3WcC/W5a2AxSDaCaevlyNlcZt7Blw0QJTe3+Nyx6fZJZW5hvDw4sVENjkRuqKKMqhWGUy4PfSjCukM1B8M3h8fj4wIDkWO8My1sOrjAbAxfEgKsBw64AvbR7eLTXvnqhk5Fi1zh9emEqckZFiJ+hg01AmVLDJM4FlsYEeybKYzgJNQharbE5br5bXvNZcFG7JLlkdzJ6OptS5cTVoOAKA5AU+yRMqOTiOoaElsI2dWiS9bhbECZxFdD0+pvODGYQ4pPR8NiPJEenqaYCmwEd2MokjqIbJHKHylaOatKCa7M/xy48vGi2g3oM2H4apteS5eIJhlS3LKapf3z+rKmVcyF5U8um5rjdcAr2JmOciLchbAVZ+XCAackwnbZ0Kb3ZwbaH6ZPnTpK1g1nQka9mVVMb8caJM27R9VO0dBpQUWS0ebPVX59uqR6nAniUDVrtb1rBRBs8eLonh3Q0m1mWU55K9BS2VeXo6pDJOmznm7fKQj5bnqg3IFYLTdfFflgxqudYfGHG8qoOX7n/fi/M3AlFMuBpZvHcPTosLOmTWQaERrakgiCsFy7whBgNx4dQ9cn66ZPHeAdRFQFhYK+wf50tQWfELGXsta76PUKWBIPRMADZX6OnWa5RHa5SkiuCRUUEJJYYHoNDbMS1FzSvSfBqePi/JHoZyZIFRWjwfgm2b5O3By/Gw+BwOPppvDf5enXT3PU+977wvvIC78ibeN97p96ZF3l/eH95f3v/7OzvnO6c7/zSmt6+tcJ85nWeHfYvuOK0Dg==</latexit>
N
⇥
x1 x2
⇤
=
⇥
1x1 2x2
⇤
Norm. Lap. N = D-1/2LD-1/2. Random walk Lap. LD-1.
D = diagonal degree matrix, A = adjacency matrix, L = D – A is graph Laplacian..
<latexit sha1_base64="POsukIjAahItuceyxYGW6/9e3Cc=">AAAHXnicfVVRb9s2EFbbLem8dU27l2F7YZca6FrZsdNlaQYEMLCgWIAUy2anLWB5GSWdJMIkpZFUIo8QsF+z1+3v7G0/ZUfbWS0nGwFJFHnfd7zvjmRYcKZNr/fXrdt33nt/Y/PuB60PP7r38f2tBw9f67xUEZxFOc/V25Bq4EzCmWGGw9tCARUhhzfh9Fs3/+YClGa5HJlZARNBU8kSFlGDQ+dbnz1+EoRgKDkmz8jJ0U+206+/rMghuXh8vrXd6/bmjVzv9JedbW/ZTs8fbPhBnEelAGkiTrUe93uFmViqDIs41K2g1FDQaEpTGGNXUgF6YudB1KSNIzFJcoWPNGQ+2lqFII+iswaLNTQsOVVVczTM8ynO6LqBHzuNtCxFCApiX5UcYlwcT3PFTCZ2Yc28NMmLiWWyKA3IaLHApOTE5MQpSWKmIDJ8RpqrNGz6qy9ZBImikU+FFtRkfsFcVL6gU4iA88V6nSlnoaJq5oLLL7UfIkuq8lLG2i+oMaCkRpRRrPJ1RgvQfsKMH1Eeuf/YYQqeG0HVVP8Xa1dghnFyrikHY0dlYuBHiGuLSjx60XsUcvS7amEySBWArO3842wuM2ZgzSbkJdTWvVcsWm2SGVPob3Z2DFRdbZAbqiijMoVulIudX0rQrvz0Tv/rvYPdgx0NgmGVhliUonOJ2ei4IDpMdkKsZVBzu+f724tPK3AyUqx1p08rSHkeUh7gb+BgA5C6VDCIc46lMcBKj/IYDgMFnFZX2BwX3yyv8ag/sS5JLtmNjJ6OhlQ6cRVIuMQABJWxDRIqGJ/FkNCSm9oGOrnqNwtCJ64C6lZ71ZnGDEJ82Ose+JFg6DRVlONmQAem0omjaAaJ3IE0laMaLMBWPx3jLtyb1OtBHQFuPwXDmQhz/hJDsgsWXdvvX53UVjoXgtVW1JbhcoMhmJuMcSBeh4RLyNKHAwzLENNpSpfSmx2sexi+fOUkuXIw6jfks2FVW83fOXHGC7Q9RkunAeVFRut3S/35eE31OOXAoqyz0P6mGUy0xoOneXIIR7OaZTFkqUBPwaKqHJ0NQmGDxXh9rSzECZ6+8U2I5UTddPE0qEKqxlh8QRbmlQ0u3LvdCjJ3QpEMWJoZPHf39wpD2mSUAaGRKSknCGsFUzwhet3dPaja5Kq1yRHeHFRGQPBsv8T962wJOiN6LmNr4ardImRO0Ol1+yDaV+hhlitUh8mU5JJgUREOiSGaxeAQK3Ft9+t/SfBqeP6/JGoeyZwFRajxfumv3ybXO693u/29bu+H3e3BV8ub5q73ufeF98Tre/vewPvOO/XOvMj7zfvd+8P7c+PvzY3Ne5v3F6a3by0xn3iNtvnpP4mhlL0=</latexit>
( I + LD 1
)x = v](https://image.slidesharecdn.com/2020-10-23-tamu-201023164345/85/Computational-Frameworks-for-Higher-order-Network-Data-Analysis-51-320.jpg)