eee499

1. ii List Of Figures:
Figure 1.1 multitone test principle..................................................................................... 7
Figure 1.2 Example of 7 frequencies multitone on time and frequency domain.............. 8
Figure 1.3 Audio testing with multitone .......................................................................... 8
Figure 2.1 Single tone test ............................................................................................... 10
Figure 2.2 two tone test................................................................................................... 11
Figure 2.3 multitone test for band bas filter.................................................................... 12
Figure 3.1 Test for linear device with single tone and how it act..................................... 14

2. Figure 3.2 Test for non linear behavior device with single tone and how it act .............. 15
Figure 3.3 the behavior of single tone used to test amplifier in linear region................ 15
Figure 3.4 the act of single tone use to test amplifier in non linear region .................... 16
Figure 3.5 the intermodulation distortion which appear in tow tone testing ................ 18
Figure 3.6 Themultitone output in time domain when constant initial phase used in all tones
........................................................................................................................................... 19
Figure 3.7 Themultitone output in time domain when random initial phase used in all tones
........................................................................................................................................... 20
Figure 3.8 A multitone signal in time and frequency domain ......................................... 21
Figure 3.9 the five measurements obtained from audio testing ..................................... 22
Figure 3.10 the appearance of one tone in time and frequency domain........................ 26
Figure 3.11The frequency response of 13 different frequencies using single tone test. 26
Figure 4.1 Multitone signal with high crest factor........................................................... 30
Figure 4.2 Multitone signal with low crest factor .......................................................... 30
Figure 4.3 generation of multi tone signal in matlab. The number of tones used 4 with the
highest tone frequency is 10 MHz.................................................................................... 31
Figure 4.4 time domain representation of multitone signal with 32 tones ................... 32
Figure 4.5 multi-tone signal with random phase noise. ................................................. 33
Figure 4.6 Magnitude spectrum of the output of the parallel RLC circuit when test with 4 tones.
........................................................................................................................................... 34
Figure 4.7 Magnitude spectrum of the output of the parallel RLC circuit when test with 32
tones.................................................................................................................................. 35
Figure 4.8 Circuit under test with defects tested with 32 multi-tone test signal........... 36
Figure 5.1 Series Tuned Colpitts VCO (Clapp VCO)……………………………….…38
Figure 5.2 the VCO circuit connected in white board………………………………..…39
Figure 5.3 BPF (RLC parallel circuit ) ………………………………………...………40
Figure 5.4 part (a) parallel RLC output with C= 2.2 μF part (b) same filter but di...….41
Figure 5.5 RLC series BPF output shape ……………..…………………………….…41
Figure 5.6 multitone signal in time domain……………………………………..…….44

3. Figure 5.7 multitone signal using the DSP kit and picoscope in time domain ………..45
Figure 5.8 multitone spectrum before testing the filter………………………………..45
Figure 5.9 Testing the BPF using the DSP kit……………………………………….…46
Figure 5.10 show the spectrum after testing the BPF using picoscpe……………..…...47
Figure 5.11 the spectrum of BPF after the test…………………………………………47
Figure 5.12 spectrum of BPF when changed the value of capacitor…….………….….48
Figure 5.13 spectrum of BPF when changed the value of capacitor……….……..……49
iii Abstract
Multitone testing represent an advanced technique used for testing electronic
devices whether it can be passive devices like filters or active like amplifiers and
diodes, accordingly this test done for linear and nonlinear behavior devices, so in
this report we aim to apply this test to linear device like band bass filter (BBF).
Multitone testing considered as a sophisticated method because of the number of
tones used to test device under test (DUT) more greater than traditional

4. technique like single tone and two tone testing. This test stand for an operation of
generating multitone signals consist of a summation of sine waves connected to
the DUT which are connected to spectrum analyzer to obtain the frequency
response and analyze it for the tested device,if it satisfied the determined
specification needed ,then we decide to accept this device or neglect it by
calculating a crest factor (CF) which give us an important indication about our
judge and this practicability one of many applications of multitone testing.
Moreover, this test considered as a practical mechanism done in manufacturing
of electronic devices before product launch in the market to make sure the
productmeets the specifications that labeled to this item.
• Chapter1
• Introduction
• Overview
Modern appetites for increased information from wireless devices has driven the complexity of
communications modulation formats, as well as the complexity of the signal sources needed to
test those communications systems. Advanced modulation formats often cannot tolerate
linearity shortcomings of components in those systems, often visible as unwanted
intermodulation distortion (IMD). Testing active and some passive components for
susceptibility to IMD usually requires multitone test signals. While securing a rack of laboratory-
grade signal generators can be expensive, multitone test signals can be generated cost
effectively. Doing so requires a proper review of an application’s requirements and assembling
a multitone test source that is flexible, practical, and accurate.

5. This principle of using multitone signal allows acquiring the result of several measurement
functions at different frequencies in a single step only.
At the case of single tone and two tone testing represent a traditional technique for testing
devices, these test no longer appropriate because it take longer time to achieve the test by
forcing us to change the input frequency of the signal generator each time, furthermore these
test have less accuracy of it results since it depends on one or two tone as a maximum case to
check the frequency response output appears on the spectrum analyzer.
Nowadays because of the enormous development in communication and the huge demand of
electronic devices in all over the world the previous technique down and anew one arises in the
environment of the communication meet the spread of advanced manufacturing of electronic
products through the productivity stages called multitonetesting which stand for a powerful
approach is the use of a multitone signal as stimulus.
This principle allows to acquire the result of several measurement functions at different
frequencies in a single step only, although this mechanism aims to overcome the time
bottleneck.
It bases on the principle of simultaneously transmitting all the sinusoidal tones -frequencies- of
interest in a single burst. This stimulus is called ‘multitone signal’.
In a typical multitone measurement, the generator sends the user defined burst through the
DUT to the analyzer as in .
Figure 1 1.1 multitone test principle

6. Figure 2 shows two pictures represent a multitone signal with 7 frequencies, displayed on an
oscilloscope in the time domain and on a spectrum analyzer in the frequency domain
respectively:
Figure 2 1.2 Example of 7 frequencies multitone on time and frequency domain
Also multitone used in most audio test instruments stimulate the device under test (DUT) with
a single sinusoidal wave. By analyzing its output signal, one test result per frequency - e.g.
Distortion or Noise - may be acquired. Another, more powerful approach is the use of a
multitone signal as stimulus. This principle allows to acquire the result of several measurement
functions at different frequencies in a single step only. Figure 3 shows how multitone testing
used in audio:
Figure 3 1.3 Audio testing with multitone

7. • Existing Problems
• The key problems that necessitate carrying out this project can be summarized as
follows:. Solving the time and cost issue by finding a way that used for generating a
multitone signals unlike traditional test which need a lot of time to achieve.
• Finding a way for characterizing the linear and non linear behavior to solve the
intermodulation distortion and the harmonics.
• Writing an efficient code using matlab could be able to detect if the device is faulted or
not.
• Knowing the characteristic of the channel that the multitone signal transmitted then
passing throw a channel to test the device under test (DUT).
• Motivation for Carrying out the Research
The main objectives of our project and report are to gain experience in team working and to
practice many aspects of Scientific Research, Web Search and Technical Writing.learn how to
deal with problems you faced during the work and try to use the knowledge we get in practical
way to release the different between the theory and the application. Learn newer methods that
are used in producing companies to examine the electronic devices and try to find a new way
to apply this test with short period of time to test device ,also this way has less cost due to
other traditional techniques.

8. • Chapter 2
• Methods used to test DUT
•
• 2.1 Single tone measurement
This test is simple since it depends on one signal need to test DUT and then characterizing the
out of spectrum analyzer figure 4 demonstrate this test:
Figure 4 2.1 Single tone test
The most striking advantage of single-tone measurements is simplicity:
• It allows the performance of a DUT to be evaluated over a range of frequencies with a
single tone measurement.
• The characteristics of a multitone waveform (e.g., spectral content, crest factor, etc.)
give it a much closer resemblance to typical audio program material like music or
speech, than a single sine wave.

9. •
• 2.2 Two tone test (measurements):
Similar to single tone test but we use tow tones to get the output as shown on figure 5.
Figure 5 2.2 two tone test
This test usually used for third-order intermodulation distortion (IMD3) which represent the
measure of the third-order distortion products produced by a nonlinear device when two tones
closely spaced in frequency are fed into its input. This distortion product is usually so close to
the carrier that it is almost impossible to filter out and can cause interference in multichannel
communications equipment.IMD is measured by examining the output of a device under test
(DUT) with a spectrum analyzer while the DUT is being stimulated with a two tone test signal,
when characterizing the nonlinear behavior of an amplifier. Two discrete tones with equal
power, that fall within the pass band of the DUT, are applied to the input of the DUT as in figure
5.
The resultant harmonic and intermodulation distortion products are then measured using a
spectrum analyzer.

10. • 2.3 Multitone test:
This represent an advanced test which could be more complicated compared with the previous
tests. For example if we want to generate a multitone signal (200 sine waves combined to each
other in the conventional test mentioned before this idea has one meaning that we need 200
signal generators to generate multitone signal and this action requires a lot of money and time.
In this project the signal generator which give us the multitone replaced by constructing a code
in matlab meets our requirement of getting the multitone signals. In this project the multitone
signal represents the test stimulus for the device under test DUT. The DUT parameters are
extracted by using a spectrum analyzer from the DUT output, we can compute the crest factor.
The crest factor can be considered as a good indicator to decide if the DUT meets the desired
specifications or not. Figure 6 demonstrate the terminology of what we conduct in this project:

11. Figure 6 2.3 multitone test for band bas filter
•
• 2.4 Advantages of multitone test
The basic principle of saving time and money through using multitone testing mechanism is to
compare it with the conventional tests used to done before .In the traditional methods like
single and two tone measurement to conduct a test for any device this operation takes a lot of
time since at these test we must have at least one signal generator at the case of single tone
and every time we need to wait for the first frequency generated then analyze the frequency
response output whole this process done for the first frequency generated but these test
depends in using several frequency so we need to generate a new frequency then repeats the
complete steps for several times .
In tow tone testing measurement we need two signal generators connected to the tested
device to obtain the output, similarly the same problem still stand that we need to change the
input frequency of generator every step.
If we want make the test faster by generating more than one frequency in one step this mean
we need a large number of signal generators each one tuned with different frequency than
others with a combiner all connected to DUT and this technique if it is actually reduced the
time but increase the price of achieving this test and it needs a huge budget.

12. On the other hand , in multitone approach we can generate multitone signal simply by writing a
code in matlab this operation represent the multitone signal itself and apply this code for the
tested device to get the frequency response output which we could analyze it by using matlab,
the result we obtain from this test doesn’t take a lot of time , and this meets the requirements
needed in the global factories which specialize of producing electrical devices with its variety in
all applications since multitone testing represent an advance technique achieve three
important factors in a consecutive way accuracy ,speed in taking result , low cost technique.
•
• Chapter 3
• Application of multitone testing
• 3.1 Testing linear and non linear devices like band pass
filter, amplifier….etc.
We decide in this project to work on testing linear device using multitone signal to conduct this
test well as possible. Therefore we should gain a good understand of linear and non linear
behavior concepts of the tested device. Devices that behave linearly only impose magnitude
and phase changes on input signals. Any sinusoid appearing at the input will also appear at the
output at the same frequency. No new signals are created. When a single sinusoid is passed
through a linear network, we don't consider amplitude and phase changes as distortion.
However, when a complex, time-varying signal is passed through a linear network, the
amplitude and phase shifts can dramatically distort the time-domain waveform. Figure 7 shows
how single sinusoidal act through a device has a linear action :

13. Figure 73.1 Test for linear device with single tone and how it act
Unlike linear behavior, non-linear devices can shift input signals in frequency (a mixer for
example) and create new signals in the form of harmonics or inter-modulation products. Many
components that behave linearly under most signal conditions can exhibit nonlinear behavior if
driven with a large enough input signal. This is true for both passive devices such as filters and
even connectors, and active devices like amplifiers. Figure 8 shows the effect of nonlinear
behavior .
Figure 83.2 Test for non linear behavior device with single tone and how it act
To understanding the matter of distortion in both cases of devices behavior we enter a single
sinusoidal cosine wave through an amplifier.
In linear region only the amplitude increased as seen in figure 9.

14. Figure 9 3.3 the behavior of single tone used to test amplifier in linear region
On the other hand,
the intermodulation harmonics clearly appears when the amplifier received an input, the most
critical out-of-band distortion is typically the 2nd order and 3rd order distortion. If we develop
the 2nd order and 3rd order terms in the Malaren series for a single tone input, we obtain
distortion terms at the multiples of the fundamental frequency. These correspond to the 2nd
order and 3rd order harmonics .Harmonic distortion is typically specified relative to the
fundamental level. If the fundamental power level changes by a certain amount in dB, the
power level of 2nd and 3rd order harmonics changes by twice or three times the same amount in
dB, respectively. For example, for a 1 dB increase in the fundamental results in a 2 dB increase
of the 2nd harmonic and in a 3 dB increase of the 3rd harmonic. This means that the relative
level of the 2nd harmonic to the fundamental will be 1 dB larger than it was, and the relative
level of the 3rd harmonic will be 2 dB larger. Therefore, when specifying the relative or absolute
level of the 2nd harmonic distortion, for example, it is imperative to also specify the level of the
fundamental at which the distortion was measured. Once this is provided, the 2nd harmonic

15. distortion can be theoretically predicted for any power level at the fundamental. However, this
prediction only holds true for the more linear section of the power transfer function of the
device, so it can only model distortion in devices under small signal excitation, from figure 10
we can see the harmonic distortion represent in nonlinear region.
Figure 10 3.4 the act of single tone use to test amplifier in non linear region
Now we will see if more than one frequency enters to amplifier at the case of non linear region.
The two-tone continuous wave distortion measurement is the most common test used to
characterized the 3rd order IMD in a device .also two-tone signals are used extensively in the
communications industry to test for nonlinear distortion at the component, device, sub-system,
and system level.
Intermodulation distortion -IMD- is a particular type of nonlinear distortion; other types include
harmonic distortion and cross modulation. IMD is the primary cause of in-band and out-of-band
spectral regrowth (i.e. distortion) and results from unwanted intermodulation between the
multiple frequency components that comprise a signal. Intermodulation occurs as a result of
the signal traversing components and devices with nonlinear transfer functions.
Intermodulation (IMD) is the formation of combination frequencies resulting from a nonlinear
transfer characteristic when the input signal comprises several frequencies. The 3rd order
intermodulation products are typically the most problematic, since their frequencies are
relatively close to the fundamental frequencies. As with any 3rd order distortion, when the
power level of the fundamental increases by a certain amount in dB, the power level in dB of
the IMD will increase by three times that same amount in dB, or its relative level to the
fundamental will increase by twice that amount in dB. Therefore, when specifying the relative
or absolute level of 3rd order IMD, the level of the fundamental must also be specified. Once
this is provided, the 3rd order IMD can also be theoretically predicted for any power level at the
fundamental.

16. Figure 11 shows the intermodulation distortion which occur for non linear device like amplifier
using two tone measurement and shows the IMD products generated when two tones at
frequencies f1 and f2 are presented to the input of a nonlinear device.
Figure 11 3.5 the intermodulation distortion which appear in tow tone testing
It is obvious that tow tone measurement represent a strong technique for characterizing inter
modulation distortion, because of that nonlinear behavior is important to quantify, as it can
cause severe signal distortion. Common nonlinear measurements include harmonic and
intermodulation distortion (usually measured with spectrum analyzers and signal sources). IMD
is measured by examining the output of the device under test (DUT) with a spectrum
analyzerwhile the DUT is being stimulated with a multitone test signal.
Multi tone signals also affected by the relationship of the phase of each tone, so considering
the phase of multitone is zero or adding phase to these signal directly affect the peak value of
the output signal and the average value which directly affect the crest factor .also affect the
IMD measured at a specific frequency varies widely depending on the phase relationships of the
tones that comprise the test signal.

17. So when summing multiple frequencies, the phase relationships of the frequency components
affect the time-domain profile and peak-to-average characteristics of the composite signal.
Figure 12 shows the composite signal when all the tones have the same initial phase :
Figure 12 3.6 Themultitone output in time domain when constant initial phase used in all tones
Figure13 shows the composite signal when the tones have a random initial phase setting.
Although IMD is noticeably dependent of the phase relationships of the tones, IMD
Test results from one phase set are not predictive of IMD test results from another phase
Set based on phase relationships of the tones or peak-to-average ratio of the composite
Signal; in other words, IMD test results are not strongly correlated to the phase relationships of
the tones in a statistical sense. Consequently, as the phase relationships of the spectral
components in the pass band of the DUT vary over time, the nonlinear distortion characteristics
of the DUT vary in an unpredictable manner. As a result, testing with a single phaseset does not
provide enough information to adequately characterize IMD.

18. Figure 13 3.7 The multitone output in time domain when random initial phase used in all tones
•
• 3.2 Audio testing
The trend in modern audio testing is to reduce more and more the time required for complete
performance test of the device being tested. This tendency results partly from the demand of
broadcasters being forced to provide 24hour programming, leaving little time for testing. Most
audio signal measurements are performed by stimulating the device to be tested with a test
signal and analyzing the transmitted signal as soon as it has passed the device. One must be
aware that the result of this evaluation consists of a few core quantities only, all of them
relating to the capabilities of the human hearing sense. More advanced tests such as
intermodulation distortion measurements stimulate the device with a pair of sinusoidal signals
to come closer to the real situation of audio signal transmission.
In the presence of nonlinear transfer characteristics, the DUT generates new harmonic and
intermodulation frequencies.
However, in practice the device is normally stimulated by music or speech which is a far
More complex signal than any single or twin tone test. Many frequencies with non-correlated
phase relations exist in such a real-world signal.

19. Therefore, multitone testing is a much more realistic approach for audio testing, emulating the
complex structure of natural sound. A multitone signal typically contains 2 to ~31 signal
frequencies, each with a certain phase relation, distributed over the frequency band of interest.
Obviously, sophisticated test instruments are necessary to analyze all these signals with their
interactions on each other.
Figure 14shows a typical multitone signal in the time- and frequency domain:
Figure 14 3.8 A multitone signal in time and frequency domain
Obviously, it is necessary to characterize the time signal by an appropriate value in order to
allow the optimization of its phase relations. The most suitable measure for this purpose is the
Crest Factor (CF), which is defined as
For any multitone signal with given RMS value, the Crest factor will change with the peak value,
which in turn depends on the phases of the signal components. An optimal distribution of the
phases results in a low peak value of the resulting time signal and therefore a low Crest factor
will occur.
Alternatively, the principle of a multitone test, providing five measurement results, all acquired
in parallel at a time, may be described by following picture in fig 15.

20. Figure 15 3.9 the five measurements obtained from audio testing
These five measurements are:
• Level: it indicates the complete energy content of the test signal.
• Frequency response is the quantitative measure of the output spectrum of a system or
device in response to a stimulus, and is used to characterize the dynamics of the system. It
is a measure of magnitude and phase of the output as a function of frequency.
• Distortion: Both the Harmonic Distortion (THD+N or SINAD) and Intermodulation Distortion
test refer to new signal components or frequencies that are generated by the DUT.
The Total Harmonic Distortion (THD) is defined as the ratio between the power of the harmonic
frequencies above the base frequency and the power of the base frequency. This ratio is
displayed in dB's. It is a measure of the distortion in a signal.
The THD is calculated using the follow
In formula:

21. Where:
V1 is the signal amplitude in rms voltage
V2 is the second harmonic amplitude in rms voltage
Vn is the nth harmonic amplitude in rms voltage
SINAD: Signal to Noise and Distortion Ratio is a parameter which provides a quantitative
measurement of the quality of an audio signal from a communication device. For the purpose
of this article the device is a radio receiver.
The definition of SINAD is very simple - it’s the ratio of the total signal power level (wanted
Signal+ Noise + Distortion or SND) to unwanted signal power (Noise + Distortion or ND).
• Noise :Noise measurement is normally done with a quasi-peak detector
• Crosstalk : notice when characterizing non linear behavior especially the 3rd harmonic
distortion since it very close the fundamental frequency
In order to understand the multitone testing process and audio testing in special case, it is vital
to understand some basics of signal generation and especially the meaning of the following
concepts:
• Bins & Signal Bins
First, a discretely generated time signal of blocklength, i.e. the number of samples which build
the signal, as well as the sampling frequency fs.
The following equation shows how we calculate the possible frequencies of a time signal

22. limited length can comprise certain frequencies only. These frequencies fn is given by the
Where:
fs: the sampling frequency
n : integer number
Blocklenght: the number of samples that are actually used for one FFT
fn : the possible frequencies of a time signal.
These possible frequencies have been named bins. However, a practical
Multitone signal will almost never comprise all possible frequencies, but a user-defined
selection of them only. These actually set bins are called signal bins.
Furthermore, the bins and signal bins are normally not described by their frequencies,
expressed in Hertz, but instead by their bin number. This value is obtained by numbering all
possible frequencies starting with the lowest possible value. Alternatively, the bin numbers can
be calculated according to:
• Bandwidth
The available frequency range of the transmission path always has to be considered. It is
defined by the minimum and maximum frequency which can pass through the DUT.
• Number of Samples
The analysis of every audio parameter has to be optimized by the appropriate choice of the test
signals. For instance, a detailed frequency response requires more frequencies to be measured
than a crosstalk test, where few frequencies needed.
• Number of Signal Bins
The question about the optimum number of signal bins to be set for a certain test depends on
several parameter.

23. • In most industrial applications, it is necessary to check a few 3 to 5 selected core
frequencies only. Usually, this already allows a Good / No-Good decision, providing
enough security that all faulty samples are found.
• From another point of view, one may take into account the specific demands of the
different measurement functions. The level and phase measurement may require a
larger number of signal bins in order to get a precise representation of the frequency
and phase response. On the other hand, the distortion, noise and crosstalk test should
be restricted to a few signal bins only, resulting in more meaningful measurement
values
• Frequency Spacing
The frequency spacing f corresponds to the lowest frequency that can be generated &
analyzed. It defines the spectral resolution of the FFT and is calculated by following formula.
On the other hand, practically single tone also used a sine signal with one specific frequency,
the following graph for one sinusoidal signal fig 16.

24. Figure 16 3.10 the appearance of one tone in time and frequency domain
In order to get a characterization over the complete frequency range, the generated signal
must be swept through the band of interest, i.e. its frequency has to be increased (or
decreased) stepwise, while at every step a measurement is executed.
For instance, the frequency response of a DUT in the audio range can be evaluated with a single
tone test signal starting at 20Hz and ending at 20 kHz as shown in figure 17:
Figure 17 3.11The frequency response of 13 different frequencies using single tone test
• 3.3 Channel Estimation
In wireless communication channel estimation refers to known channel properties of a
communication link. This information describes how a signal propagates from the transmitter

25. to the receiver and represents the effect which happened to the original signal, for example,
scattering, fading, and power decay with distance. Channel estimation usually refers to
estimation of the frequency (and potentially spatial) response of the path between the
transmitter and receiver. This knowledge can be used to optimize performance and maximize
the transmission rate.
In this application the multitone signal represent the input signal transmitted from the
transmitter through a channel could be a free space, coaxial cable or any medium until the
signal picked up by the receiver.
• Chapter 4
• Simulation
•
• 4.1 Crest factor
The Crest Factor is equal to the peak amplitude of a waveform divided by the RMS value:
Also
Where:

26. Cf: the crest factor
VP: the peak voltage
Vrms: the rms value.
The purpose of the crest factor calculation is to give an analyst a quick idea of how much
impacting is occurring in a waveform.
When measuring a DUT with a test signal, we usually don't think about the peak value of the
signal, it makes sense when we remember that the peak level of a sine wave equals
approximately 1.41 times its RMS value.
However, things are different when working with multitone signals that are put together by two
or more sine waves with different frequencies. In such cases, the resulting time signal, which is
obtained by adding its components, will show a much larger difference between its RMS and
peak value.
In order to allow the characterization of a signal, a relationship between its peak and its RMS
level had to be established, the so-called Crest factor Cf. It indicates the ratio of the peak level
of the signal to its RMS level. Consequently, a high Crest factor corresponds to a signal having a
high peak voltage compared to the average signal level.
Different multitone signals have different Crest factors, depending on the number
of signal bins and the phase relations between them depend on the chosen phase relationship.
Furthermore, it is vital to know that the higher the Crest factor of a multitone signal, the poorer
the signal to noise ratio of the measurement. This can be explained easily when considering the
shape of a multitone signal with a high Crest factor. As we see in figure 18, the peak value of
the signal is far above its average (RMS) level. Obviously, when transmitting such a signal
through a DUT, one must adapt the peak voltage of the signal to the max. Allowable voltage of

27. the DUT in order to avoid clipping. Consequently, the RMS voltage of the signal becomes very
small, thus coming closer to the noise floor of the transmitted signal.
.
Figure 18 4.1 Multitone signal with high crest factor
So if we look to the same multitone signal, but this time with optimized phase relations
between its signal bins, displayed in figure 19.
This time, the difference between the peak voltage of the signal and its RMS level has
become much smaller. This does not only reduce the necessary headroom for signal
transmission, but also improves the signal-to-noise ratio by far.
Figure 19 4.2 Multitone signal with low crest factor

28. As a conclusion, the Crest Factor is a quick and useful calculation that gives the analyst an idea
of how much impacting is occurring in a time waveform.
• 4.2 Generation of multi-tone signal
In this section, the multi-tone testing algorithm will be applied to a linear passive network. The
linear passive network chosen to test the multi-tone stimulus is a parallel RLC circuit.
For example if we use a multi-tone signal composed from four tones with the highest tone
frequency is 10 MHz, then the resulting multi-tone signal appears as shown in :
Figure 20 4.3 generation of multi tone signal in matlab. The number of tones used 4 with the highest tone
frequency is 10 MHz
The crest factor for the multi tone signal shown in is. If the number of tones is increased to 32
with the highest tone frequency of 10 MHz, then we can see the peak of the multi tone signal
became larger and its period also became larger as shown , while the crest factor increases up
to.

29. Figure 21 4.4 time domain representation of multitone signal with 32 tones
The above generation for the multi-tone signal assumes zero phase for the generated signal.
Multitone signal with large crest factor is undesirable for applications with the nonlinearity.
However the crest factor can be reduced by adding phase noise to multi-tone signal. This
concept can be illustrated by re-simulating the previous 32 tones with random Gaussian noise
added to the phase of each tone. The simulation result is shown in . A comparison between
and shows that the peak amplitude of the multi-tone signal with random noise is much less
than the peak amplitude of the signal. The crest factor of the multi-tone signal with phase noise
is 2.81 compared with 5.33 for the multi-tone signal without phase noise.

30. Figure 22 4.5 multi-tone signal with random phase noise. The number of tones is 32 similar to that shown in
•
•
•
•
•
•
•
•

31. • 4.3 Testing the a linear circuit with multi-tone
In this section, testing a parallel RLC circuit with the multi-tone signal will be used to
demonstrate the concept of multi-tone test. The values of R, L and C where selected to model a
band pass filter whose center frequency is and its bandwidth is. In particular the values of RLC
are selected as, and the circuit is first tested with a multi-tone signal composed from four tones
added with phase noise. The output of the circuit is analyzed with Fourier transform to show its
frequency response.
Figure 23 4.6 Magnitude spectrum of the output of the parallel RLC circuit when test with 4 tones.
The magnitude spectrum of the signal detected at the output of the circuit under test is shown
in . From , we can see that there spectrum of the tested circuit is centered about 5 MHz, but the
bandwidth is not properly represented or clarified. If the number of tones is increased to 32
tones, then the resulting signal appears as shown in Figure .

32. Figure 24 4.7 Magnitude spectrum of the output of the parallel RLC circuit when test with 32 tones.
From , it is clear that the spectrum of the tested signal is properly identified. As a result to this
discussion we can see that the as the number of tones is increased we can estimate the
characteristics of the device under test properly.
The crest factor measured at the output of the device under test (parallel RLC circuit) when it is
excited by the 32 tones is.
If we assume that the circuit under test is subjected to manufacturing defects, such that its
center frequency is altered, then the crest factor will change as. The change in crest factor will
indicate that the circuit under test is defected. To demonstrate this results assume that the
inductor value is changed from the to. If the circuit under test is tested again with the 32 tones,
then the resulting magnitude spectrum is shown

33. Figure 25 4.8 Circuit under test with defects tested with 32 multi-tone test signal.
We can see that the center frequency of the defected circuit is not 5 MHz also the crest factor
is. If we compare the crest factor for the circuit with no defect with the defected circuit we can
see a clear difference between them (almost 12.5%). Since analyzing the spectrum of the circuit
under test each time the circuit needs to be tested will take long time for performing the
analysis and comparison. The crest factor represents a faster testing method to determine
whether the circuit under test is defected or not. This testing technique can save time with the
number of devices to be tested is very large (approaching 1 million or larger). For this reason
testing with multi-tone and crest factor analysis is recommended for large volume production.
•
•
•
•

34. • Chapter 5
•Experimental work
• 5.1 Building a VCO (voltage controlled oscillator )
In this chapter we aim to check if the results of theoretical and apply it in practical , by
conducting tow experiment in order to generate the multione signal and use it to test RLC
circuit make sure that our results will be matched by theoretical results ,accordingly these
practical two experiments building a voltage controlled circuit (VCO) and generating the
multitone using dsp kit in the DSP lap to prove that using multitone test to check the DUT is
better than single tone and two tone and getting the results and analyze it ,this test can save
time and give more accurate results and more than one measurement .
Building a voltage control oscillator (VCO) circuit :
The aim of building a VCO circuit to gain a good range of frequency in order to test the DUT by
changing the input voltage which leads to change the output frequency .
Basic oscillator design specifications often require a given output power into a specified load at
the design frequency. The drive level and bias current set the fundamental output current and
the oscillation frequency is set by the resonator components.
Transistor selection of the transistor should consider noise, frequency, and power
requirements. Based on the particular device, the design may account for parasitics of the
device affecting resonator components as well as nonlinear performance specifications.

35. To get a low phase noise we should Maximize the power at the output of the oscillator, Choose
a varactor diode or any device could Meet the same purpose with a low equivalent noise
resistance.
We choose a Series Tuned Colpitts VCO (Clapp VCO) topology to be the circuit which we
conducted in this project as shown below :
Figure 26 5.1 Series Tuned Colpitts VCO (Clapp VCO)
The series-tuned Colpitts circuit (or Clapp oscillator) works in much the same way as the parallel
one.
The capacitor, C1, is positioned so that it is well-protected from being swamped by the large
values of C3 and C4.
In fact, small values of C3, C4 would act to limit the tuning range. Fixed capacitance, C2, is often
added across the varicap to allow the tuning range to be reduced to that required, without
interfering with C3 and C4, which set the amplifier coupling.

36. The series-tuned Colpitts has a reputation for better stability than the parallel-tuned original.
Note how C3 and C4 swamp the capacitances of the amplifier in both versions.
we apply the VCO circuit and connected in white board to get the desired range of frequency
wanted as seen in the following graph :
Figure 27 5.2 the VCO circuit connected in white board
We found that our output range of frequency of the series tuned VCO obtained from the circuit
which shown on the digital oscilloscope 19.34 MHz to 22.75 MHz which mean it can cover a
range of frequency around 3.5 MHz .
This range was not enough to test the BBF and the frequency was very high compared to DSP
kit ,so we decide to use a frequency generator as a VCO to test the RLC circuit .In order to get
the VCO principle and apply it on our circuit we need two function generators , we use one of
them to get a ramp signal to the BBF and we will draw the changing in voltage when we change
the frequency in a graph and we will see if we get exactly the shape of band bass filter or not .

37. •5.2 Building a BPF (RLC parallel circuit )
At this stage we will build a band pass filter (RLC) to get these specifications:
Band width = 4 KHz , cutoff frequency (Fc) = 10 KHz
Accordingly the values of R,L and C calculated from these equations:
And we find R = 1k Ω,L = 0.25μF, C=1mH
Figure 28 5.3 BPF (RLC parallel circuit )
After we connect the RLC circuit we use it to be tested by the VCO which we build it to
implementation the principle of single tone , and test by multitone using the DSP kit .

38. Figure 29 5.4 part (a) parallel RLC output with C= 2.2 μF part (b) same filter but di
we notice from figure 29 part (a) that we
use the principle of single tone by using a function generator with ramp output to test the RLC
parallel circuit and the output was typically a BPF with fc=12.33 kHz and the circuit has And we
find R = 1k Ω,L = 0.25μF, C=1mH while part (b) same filter but we changed the value of C we can
see that the output is defected ,also the center frequency changed in order to get the output
correct which it is the shape of BPF we need to change the frequency from the function
generator to get the correct BPF and this action take a lot of time due to manual calibrating.
Figure 30 5.5 RLC series BPF output shape

39. This graph show how could the output signal of series RLC circuit (BPF) which appears clearly .
•5.3 Generating the multitone signal using DSP kit
This principle of multitone allows to acquire the result of several measurement functions at
different frequencies in a single step only, although this mechanism aims to overcome the time
bottleneck . the multi-tone testing will be applied to a linear passive network. The linear passive
network chosen to test the multi-tone stimulus is a parallel RLC circuit
It bases on the principle of simultaneously transmitting all the sinusoidal tones -frequencies- of
interest in a single burst. This stimulus is called ‘multitone signal’.
The basic idea from both ways of test the BPF that we could get the results from the VCO circuit
and the experiment which done on DSP kit after we analyze the both sources we calculate the
Crest Factor (Cf) and the time duration to be able to judge which test is the best .
In this experiment which done in the DSP lap using DSP kit and picoscope and a program code
composer studio -CCstudio- and the procedure to generate the multitone to be able to test the
band pass filter as the following:
we convert the multitone code which was written in matlab to C language in order to deal with
code composer studio to be able to download the code on the DSP kit and after that we will see
the multitone before using the test on RLC circuit , we connect the picoscpe to see our tone and
how much the bandwidth it covers, and the code needed as the following which used in
composer studio to download it in DSP kit :
include "dsk6713_aic23.h" //support file for codec,DSK#
#include "multitone.h"

40. Uint32 fs = DSK6713_AIC23_FREQ_96KHZ; //set sampling rate
short loop = 0; //table index
short gain = 10; //gain factor
interrupt void c_int11() //interrupt service routine
{
short sample_data;
output_sample(multitone[loop]); //output data
if(++loop>128) loop=0; //reset the loop when all samples are sent to the output
return;
}
void main()
{
comm_intr(); //init DSK, codec, McBSP
while(1); //infinite loop
} //end of main
After that we take a vector contains many sample and represent the number of sample which
we want to take in our consideration to get the multitone signal to be able to check the band
bass filter .
The vector could be like that :
short multitone[]={

41. 212,
208,
102,
21,
-10,
...
…
}
This is multitone signal in time domain which we deal with without testing the RLC from
matlab :
Figure 31 5.6 multitone signal in time domain

42. This is the
multitone signal which we see from using the DSP kit and picoscope in time domain :
Figure 32 5.7 multitone signal using the DSP kit and picoscope in time domain
This one represent the multitone spectrum before testing the filter :

43. Figure 33 5.8 multitone spectrum before testing the filter
We notice that the multitone cover a range of 24 KHZ , so we will take in our design of our
band pass filter .
After that to see what happened when we connect the BPF , we take the output line of the dsp
kit and connect it to the RLC circuit and and we get the spectrum result correct , scince it has
exactly the shape of BPF .
These pictures shows the component needed to apply this experiment :

44. Figure 34 5.9 Testing the BPF using the DSP kit
Experiment in DSP lap using DSP kit .
Figure 35 5.10 show the spectrum after testing the BPF using picoscpe
Experiment work using picoscpe to show the spectrum after testing the BPF .
This picture shows the spectrum using BPF to be tested using the multitone principle:

45. Figure 36 5.11 the spectrum of BPF after the test
From this figure we find that the crest factor CF equal to 2.587 and this is the value which
represented by using a band bass filter with these specifications R = 1k Ω,L = 0.25μF, C=1mH .
It is noticed that the time to get the result in the principle of using multitone is in micro seconds
. this mean that this test can save time when we concerned of big companies .
As we said our judje to accept the device or not by calculating the crest factor so changing any
one of R,L or C should give a difference values of crest factor as shown below :
The spectrum of BPF using R = 1k Ω,C = 10pF, L=1mH :

46. Figure 37 5.12 spectrum of BPF when changed the value of capacitor

47. This lead to change the value if CF .
The spectrum of BPF using R = 1k Ω,L = 100pF, L=1mH

48. Figure 38 5.13 spectrum of BPF when changed the value of capacitor
We notice that that changing any parameter of band pass filter lead to change the crest factor
and this how companies which produce these devices use this principle to check their products
before launch it to the market.
•5.4 Results and conclusion
We find that using the multitone teqnique and the crest factor to judge for the device to be
accepted or not is an efficient way since any change in any parameters on the device lead to
change the crest factor and this what we are looking for that this test can let us compare
between any two devices easily and with a negligple time could reach to micro second .
This mean this test can give and accurate results in less time due to compare with using a VCO
and single tone principle which need more time and less in accuracy and hard to judge when
comparing between any active or passive device .

49. •
•
•
•
•
•
•
• Chapter 6
• References
[1]. KLIPPEL GmbH. http://www.klippel.de/measurements/nonlinear-distortion/multi-tone-
distortion.html. KLIPPEL GmbH in Dresden/Germany. Oct. 2006 .
[2]. Agilent Technologies. Two-tone and Multitone Personalities,Application Note 1410. USA :
Agilent Technologies, February 6, 2003.
[3]. Generation and Conditioning . USA : Agilent Technologies, December 2002.

50. [4]. NTi Audio AG. Comparing Conventiona lvs. Multitone Testing,A2 . Rapid Test.
Liechtenstein : NTi Audio AG, Mar. 2000.
[5]. Alan V.Oppenheim, Ronald W.Schafer,Joun R.Buck. Discrete-Time Signal Processing .
Upper saddle river,New Jersey : Prentice-Hall,Inc., 1999.
[6]. NTI AG. Multitone Testing,RAPID-TEST Applications. FL-9494 Schaan,Liechtenstein : NTI AG,
Mar. 2000.
[7]. José Carlos Pedro, Nuno Borges Carvalho. Intermodulation Distortion in Microwave and
Wireless Circuits. 2003.
• Chapter 7
• Appendices
%function[waveform]=mtpr_input(bin_start,bin_stop,sample_size,samp_freq,max_PAR)
clear all
clc
%for z=1:100,
clear x
tic

51. fcarrier = 10e6; % Frequency of the RF carrier 1 GHz
A = 5; % The perak amplitude of the test signal
sample_size=2^16; % Number of samples taken for simulation
samp_freq=4*fcarrier;
N_Tones=256;
% bin_start=33;
% bin_stop=256;
% max_PAR=16;
% missing=[48 72 96 120 144 168 192 216 240];
% Generating tone frequencies
freq=(fcarrier/N_Tones)*(1:256);
% m=0;
% for k=1:N_Tones,
% freq(k)=m+fcarrier/N_Tones;
% m=freq(k);
% num_tones(k)=k;
% end
%**********************************************************************
%**********************************************************************
%generation phases
thetha(1:N_Tones)=0.6+sqrt(pi)*randn(1,N_Tones);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%thetha(1:N_Tones)=0;
%load('thetha.txt')
%generatin amplitudes
amp=ones(1,N_Tones);

52. GAUSS_NOISE=0.2+sqrt(0.01)*randn(1,sample_size); %This statemnt generates a
gaussian noise signal with 0.2 mean and 0.01 variance
t=0;
Ts=1/samp_freq; % Sampling interval
x=zeros(1,sample_size);
for i=1:sample_size,
for j=1:N_Tones,
x(i)=x(i)+amp(j)*sin(2*pi*t*freq(j)+thetha(j)); % samples taken from the 256
tones
end
%
x(i)=x(i)+GAUSS_NOISE(i); % This statement adds a gaussian noise to
the multitone signal
carrier(i) = A*sin(2*pi*t*fcarrier); % The equation for the signal under test
modu(i)=x(i)*carrier(i); % modu is the signal obtained from
multiplying the carrier by the multi tones
time(i)=t;
t=t+Ts;
end
freq_x=fftshift(fft(x)/sample_size);
freq_carrier=fftshift(fft(carrier)/sample_size);
freq_modu=fftshift(fft(modu)/sample_size);
figure(1);
subplot(3,2,1)

53. plot(linspace(0,Ts*sample_size,sample_size),x);
title('Multitone signals with noise');
xlabel('time ns');
ylabel('Amplitude V');
subplot(3,2,2)
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(freq_x(1:sample_size)));
title('Spectrum Multitone signals with noise');
xlabel('Freq GHz');
ylabel('Magnitude V');
subplot(3,2,3)
plot(linspace(0,Ts*sample_size,sample_size),carrier);
title('RF carrier');
xlabel('time ns');
ylabel('Amplitude V');
subplot(3,2,4);
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(freq_carrier(1:sample_size)));
title('Spectrum carrier');
xlabel('Freq GHz');
ylabel('Magnitude V');
subplot(3,2,5)
plot(linspace(0,Ts*sample_size,sample_size),modu);
title('Carrier x dithered multitone');
xlabel('time ns');
ylabel('Amplitude V');

54. subplot(3,2,6);
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(modu(1:sample_size)));
title('Spectrum carrier x dithered multitone');
xlabel('Freq GHz');
ylabel('Magnitude V');
modu=modu';
% plot(x);
%
% inputplot=Four(x,4e9);
% %converting to db
% inputplot.amp
% figure(2);
% plot(inputplot.frq(1:8:end),inputplot.amp(1:8:end))
% inputplot.amp=10*log10(inputplot.amp.^2)
% figure(3);
% plot(inputplot.frq(2:2:end),inputplot.amp(2:2:end));
% %Root mean square power calculations
% pwr=0;
% for k=1:512
% pwr=pwr+inputplot.amp(k)^2;
% end
% rms=
figure(2);

55. % power_timedomain = sum(abs(modu).^2)/length(modu); % This equation is
intended to compute the rms of a given signal
% poervector=sqrt(power_timedomain)*ones(1,length(modu));
% Crest_Factor=max(modu)/sqrt(power_timedomain); % This equation is used to
compute the crest factor
% CFvector=Crest_Factor*ones(1,length(modu)); % Create a vector to hold
multiple values of the crest factor
% plot(CFvector);
% hold on
% plot(poervector);
% hold off
% save('C:UsersLauraDocumentsMATLABnoisy_signal_GHz.txt', 'x', '-ascii');
l=1*150e-9;
c=1*6.7e-9;
r=10e3;
num=1;
den=[l*c l/r 1];
[numd,dend] = bilinear(num,den,samp_freq)
y=filter(numd,dend,x);
freq_y=fftshift(fft(y)/sample_size);
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(freq_y(1:sample_size)));
% These statments are used to compute the crest factor based on the
% avergaepower of the signal
power_timedomain = sum(abs(y).^2)/length(y); % This equation is intended to
compute the rms of a given signal
poervector=sqrt(power_timedomain)*ones(1,length(y));
Crest_Factor=max(y)/sqrt(power_timedomain);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

56. toc
%
% save thetha.txt thetha -ascii
% copyfile('TXA.txt',['TXA' num2str(z) '.txt']);
% copyfile('thetha.txt',['Thetha' num2str(z) '.txt']);
%end
• The code used in CCstudio
include "dsk6713_aic23.h" //supportfile forcodec,DSK#
#include "multitone.h"
Uint32 fs= DSK6713_AIC23_FREQ_96KHZ; //setsamplingrate
short loop= 0; //table index
short gain= 10; //gainfactor
interruptvoidc_int11() //interruptservice routine
{
short sample_data;
output_sample(multitone[loop]);//outputdata
if(++loop>128) loop=0; //resetthe loopwhenall samplesare senttothe output
return;
}
voidmain()

57. {
comm_intr();//initDSK,codec,McBSP
while(1);//infinite loop
} //endof main
Matlab code after editing
%function[waveform]=mtpr_input(bin_start,bin_stop,sample_size,samp_freq,max_PAR)
clear all
clc
%forz=1:100,
clear x
tic
fcarrier= 24e3; % Frequencyof the RFcarrier 1 GHz
A = 5; % The perakamplitude of the testsignal
sample_size=2^7; % Numberof samplestakenforsimulation
samp_freq=4*fcarrier;
N_Tones=32;
% bin_start=33;
% bin_stop=256;
% max_PAR=16;
% missing=[4872 96 120 144 168 192 216 240];
% Generatingtone frequencies
freq=(fcarrier/N_Tones)*(1:256);
% m=0;

58. % for k=1:N_Tones,
% freq(k)=m+fcarrier/N_Tones;
% m=freq(k);
% num_tones(k)=k;
% end
%**********************************************************************
%**********************************************************************
%generationphases
thetha(1:N_Tones)=0.6+sqrt(pi)*randn(1,N_Tones);
%thetha(1:N_Tones)=0;
%load('thetha.txt')
%generatinamplitudes
amp=ones(1,N_Tones);
GAUSS_NOISE=0.2+sqrt(0.01)*randn(1,sample_size); %Thisstatemntgeneratesagaussian
noise signal with0.2meanand 0.01 variance
t=0;
Ts=1/samp_freq; % Samplinginterval
x=zeros(1,sample_size);
fori=1:sample_size,
forj=1:N_Tones,

59. x(i)=x (i)+amp(j)*sin(2*pi*t*freq(j)+1*thetha(j)); % samplestakenfromthe 256 tones
end
%
x(i)=x(i)+GAUSS_NOISE(i); % Thisstatementaddsa gaussiannoise tothe
multitone signal
carrier(i) =A*sin(2*pi*t*fcarrier); % The equationforthe signal undertest
modu(i)=x(i)*carrier(i); % moduis the signal obtainedfrommultiplyingthe
carrier bythe multi tones
time(i)=t;
t=t+Ts;
end
freq_x=fftshift(fft(x)/sample_size);
freq_carrier=fftshift(fft(carrier)/sample_size);
freq_modu=fftshift(fft(modu)/sample_size);
figure(1);
subplot(3,2,1)
plot(linspace(0,Ts*sample_size,sample_size),x);
title('Multitonesignalswithnoise');
xlabel('timens');
ylabel('Amplitude V');
subplot(3,2,2)
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(freq_x(1:sample_size)));

60. title('SpectrumMultitonesignalswithnoise');
xlabel('FreqGHz');
ylabel('Magnitude V');
subplot(3,2,3)
plot(linspace(0,Ts*sample_size,sample_size),carrier);
title('RFcarrier');
xlabel('timens');
ylabel('Amplitude V');
subplot(3,2,4);
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(freq_carrier(1:sample_size)));
title('Spectrumcarrier');
xlabel('FreqGHz');
ylabel('Magnitude V');
subplot(3,2,5)
plot(linspace(0,Ts*sample_size,sample_size),modu);
title('Carrierx ditheredmultitone');
xlabel('timens');
ylabel('Amplitude V');
subplot(3,2,6);
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(modu(1:sample_size)));
title('Spectrumcarrierx ditheredmultitone');

61. xlabel('FreqGHz');
ylabel('Magnitude V');
modu=modu';
% plot(x);
%
% inputplot=Four(x,4e9);
% %convertingtodb
% inputplot.amp
% figure(2);
% plot(inputplot.frq(1:8:end),inputplot.amp(1:8:end))
% inputplot.amp=10*log10(inputplot.amp.^2)
% figure(3);
% plot(inputplot.frq(2:2:end),inputplot.amp(2:2:end));
% %Rootmeansquare powercalculations
% pwr=0;
% for k=1:512
% pwr=pwr+inputplot.amp(k)^2;
% end
% rms=
figure(2);

62. % power_timedomain=sum(abs(modu).^2)/length(modu); % Thisequationisintendedto
compute the rms of a givensignal
% poervector=sqrt(power_timedomain)*ones(1,length(modu));
% Crest_Factor=max(modu)/sqrt(power_timedomain); % This equationisusedtocompute
the crest factor
% CFvector=Crest_Factor*ones(1,length(modu)); % Create a vectorto holdmultiple
valuesof the crestfactor
% plot(CFvector);
% holdon
% plot(poervector);
% holdoff
% save('C:UsersLauraDocumentsMATLABnoisy_signal_GHz.txt','x','-ascii');
l=2*150e-9;
c=1*6.7e-9;
r=10e3;
num=1;
den=[l*cl/r1];
[numd,dend] =bilinear(num,den,samp_freq)
y=filter(numd,dend,x);
freq_y=fftshift(fft(y)/sample_size);
plot(1/fcarrier*samp_freq*linspace(-5,5,sample_size),abs(freq_y(1:sample_size)));
xlabel('frequency,MHz');
ylabel('Magnitude,V');
% These statmentsare usedtocompute the crest factorbasedon the
% avergaepowerof the signal

63. power_timedomain=sum(abs(y).^2)/length(y); % This equationisintendedtocompute the
rms of a givensignal
poervector=sqrt(power_timedomain)*ones(1,length(y));
Crest_Factor=max(y)/sqrt(power_timedomain);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3)
plot(x)
xlabel('time,us')
ylabel('amplitude,V')
% power_timedomain=sum(abs(x).^2)/length(x);
% Crest_Factor=max(x)/sqrt(power_timedomain);
% Crest_Factor=max(x)/sqrt(power_timedomain);
toc
%
% save thetha.txtthetha-ascii
% copyfile('TXA.txt',['TXA'num2str(z) '.txt']);
% copyfile('thetha.txt',['Thetha'num2str(z) '.txt']);
%end
i=0:length(x)-1;
desired=round(25*x);%sin(1500)addnoise=round(100*sin(2*pi*(i)*312/8000));%sin(312)
fid=fopen('multitone.h','w');%desiredsin(1500)
fprintf(fid,'shortmultitone[]={');

64. fprintf(fid,'%d,n',desired(1:length(desired)-1));
fprintf(fid,'%d',desired(length(desired)));
fprintf(fid,'};n');
fclose(fid);
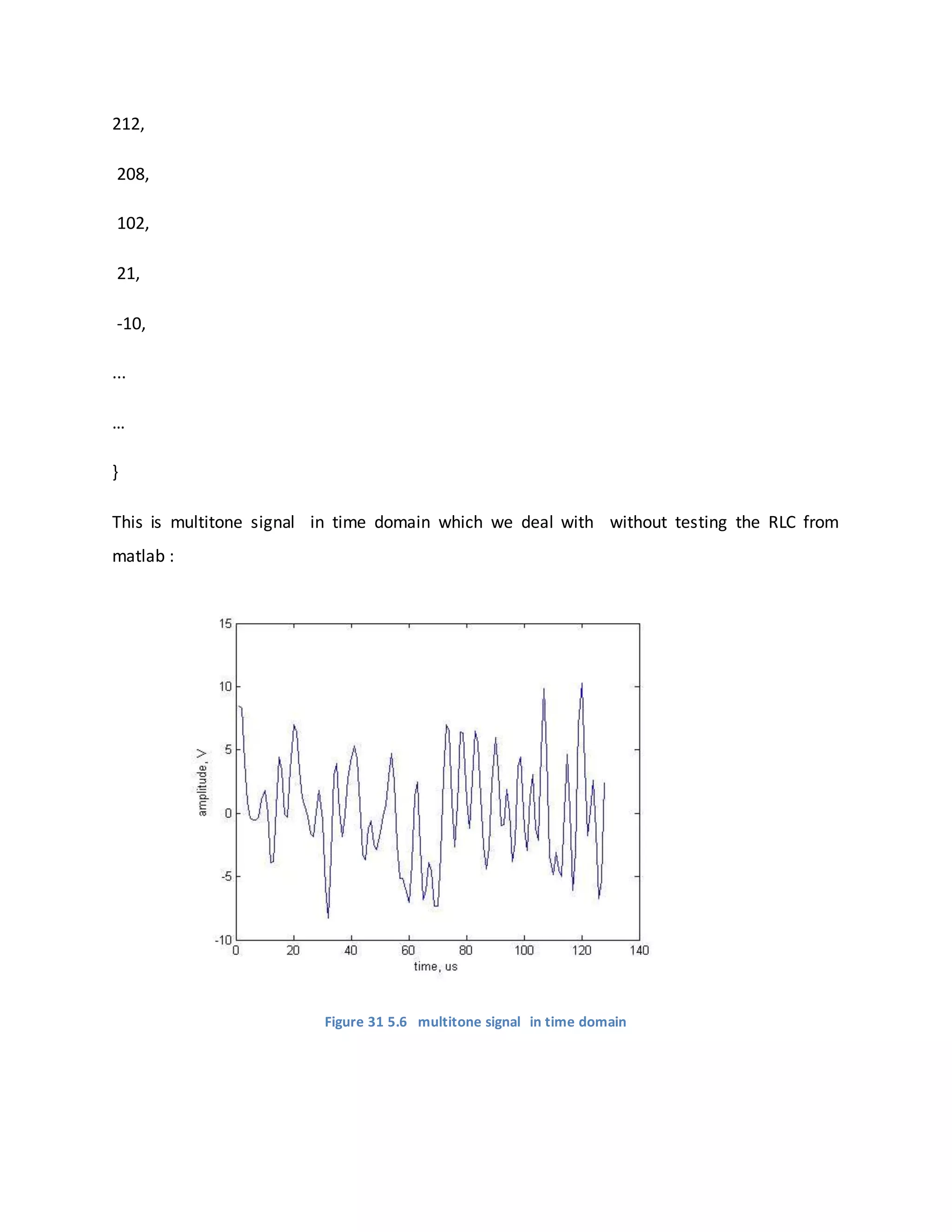
The sample vector of multitone
short multitone[]={212,
208,
102,
21,
-10,
-13,
-14,
-9,
28,
45,
0,
-98,
-96,
10,
111,
85,
-2,
-8,

65. 88,
175,
160,
85,
30,
13,
-6,
-42,
-46,
4,
45,
-15,
-147,
-208,
-82,
75,
99,
3,
-46,
-3,
68,
110,
132,
108,
19,

66. -81,
-92,
-30,
-16,
-61,
-72,
-37,
-4,
16,
73,
118,
62,
-61,
-129,
-129,
-149,
-176,
-99,
35,
61,
-66,
-171,
-152,
-97,
-114,

67. -184,
-182,
-81,
75,
175,
162,
25,
-66,
17,
161,
159,
25,
-30,
69,
163,
139,
33,
-65,
-110,
-66,
61,
149,
81,
-24,
-22,

68. 47,
4,
-96,
-57,
93,
112,
-29,
-74,
32,
77,
-29,
-53,
120,
247,
117,
-85,
-121,
-77,
-112,
-125,
4,
117,
7,
-153,
-76,

69. 175,
257,
93,
-44,
5,
66,
-35,
-168,
-132,
59};
•