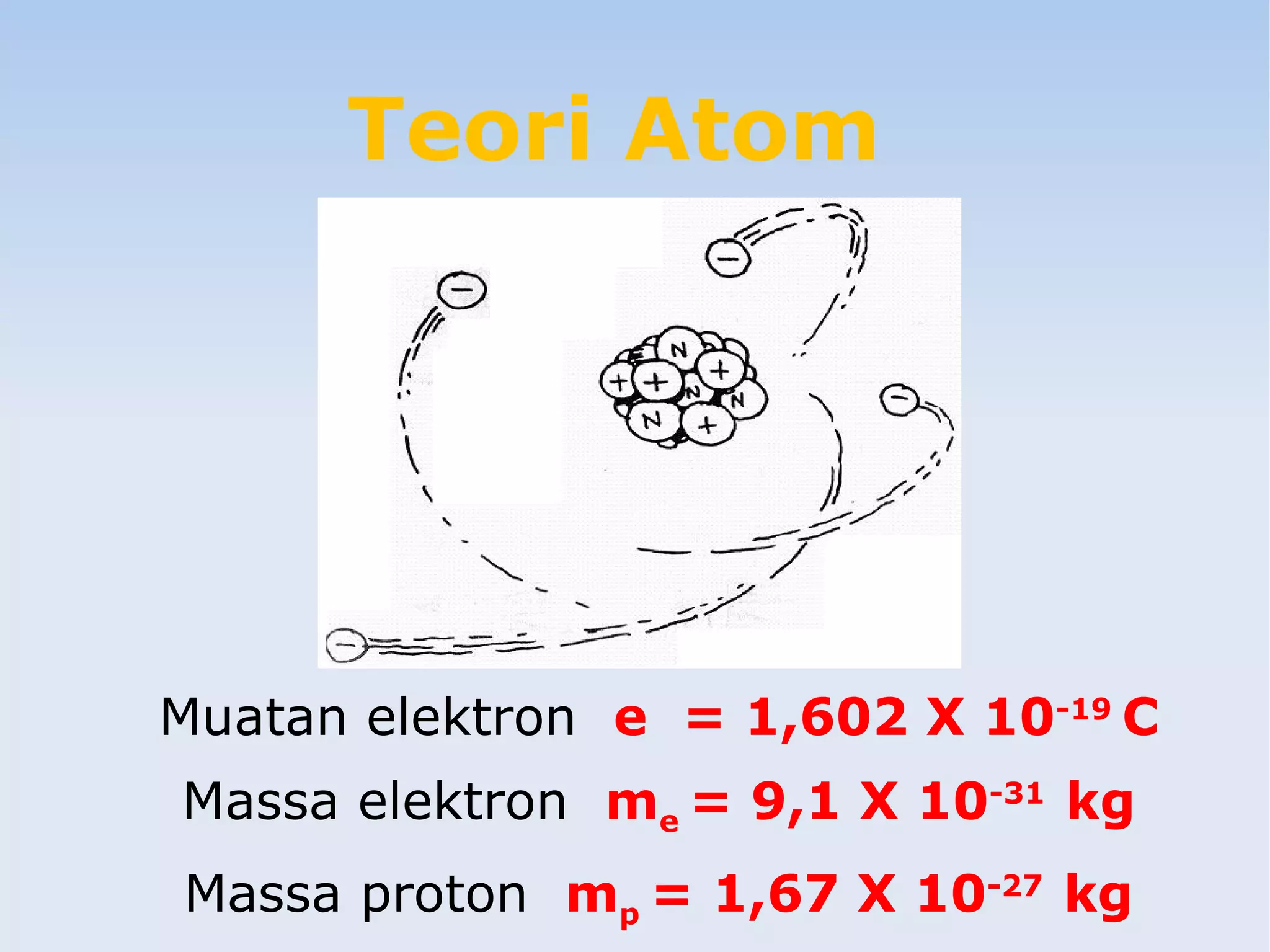
Dokumen tersebut membahas tentang muatan listrik, medan listrik, dan dipol listrik. Muatan listrik adalah besaran skalar yang menentukan interaksi listrik antara partikel, sedangkan medan listrik adalah vektor yang menunjukkan gaya listrik pada muatan. Dipol listrik terdiri atas sepasang muatan berlawanan tanda yang terpisah jarak tertentu.

1. Muatan dan Medan
Listrik

2. Tujuan
Anda mengerti tentang:

Muatan

Gaya Listrik

Medan listrik

Dipol listrik

3. Ilmu Listrik

Ilmu yang mempelajari tingkah laku
muatan

Dalam ilmu listrik, hanya dijelaskan
bagaimana muatan bertingkah laku,
bukan muatan itu apa

Muatan adalah besaran skalar

4. Teori Muatan
o Ada dua j enis muat an: positif dan
negatif
o Dua muat an posit if at au dua muat an
negat if saling tolak- menolak
o Sebuah muat an posit if dan sebuah
muat an negat if saling tarik-
menarik
o Muat an dinyat akan dengan q at au

5. Perhatian
 Muatan sejenis tidak berarti kedua
muatan tersebut identik, hanya bahwa
keduanya positif atau keduanya
negatif
 Muatan berlainan jenis berarti bahwa
kedua muatan memiliki tanda yang
berlawanan

6. Teori Atom
Muatan elektron e = 1,602 X 10-19
C
Massa elektron me = 9,1 X 10-31
kg
Massa proton mp = 1,67 X 10-27
kg

7. Hukum Coulomb
Unt uk muat an q1 dan q2 yang t er pisah
sej auh r, besarnya gaya list r ik pada
masing-masing muat an adalah
F = 1 | q1 q2|
4π∈o r 2
1 = k = 9,0 X 109
N . m2
/ C2
4π∈o

8. Strategi Penyelesaian
Soal
Hukum Coulomb
o J arak harus dinyat akan sat uan dalam
m, muat an dalam C dan gaya dalam N
o Gaya list rik adalah sebuah vekt or,
sehingga gaya t ot al pada muat an adalah
j umlah vekt or dari gaya-gaya individu
o Dalam kasus dist ribusi kont inu dari
muat an, j umlah vekt or dapat dihit ung
dengan cara int egral

9. Contoh Soal
Gaya listrik versus gaya gravitasi
Sebuah part ikel alpha mempunyai
masa m=6,64 X 10-27
kg dan muat an
q=+2e. Bandingkanlah gaya t olak
list rik ant ara dua par t ikel alpha
dengan gaya t arik gr avit asi di
ant aranya.

10. Penyelesaian
Diket ahui : m = 6,64 X 10-27
kg
q = +2e = 3,2 X 10-19
C
Dit anya : Fe / Fg = ?
J awab : Fe = 1 q2
Fg = G m2
4π∈o r 2
r2

11. Gaya Listrik
Untuk muatan q1 dan q2 yang terpisah
sejauh r, besarnya gaya listrik F pada
masing-masing muatan adalah
F = k q1 q2 Hukum Coulomb
r 2
k = 1 = 9,0 X 109
N.m2
/C2
4π∈0

12. Strategi Penyelesaian Soal
Gaya Listrik
Jarak harus dinyatakan dalam satuan
m, muatan dalam C dan gaya dalam N
Gaya listrik adalah sebuah vektor,
sehingga gaya total pada muatan adalah
jumlah vektor dari gaya-gaya individu
Dalam kasus distribusi kontinu dari
muatan, jumlah vektor dapat dihitung
dengan cara integral

13. Contoh Soal
Penjumlahan vektor gaya listrik
Dua muatan titik diletakkan pada sumbu y sbb:
muatan q1 = +2,0 µC di y = 0,30 m dan muatan
q2 = +4,0 µC di y = -0,30 m. Carilah besar dan
arah gaya total yang dikerahkan oleh kedua
muatan ini pada muatan Q = +4,0 µC di x = 0,4 m

14. Penyelesaiannya
Pertama buatlah gambar sumbu xy dan posisi di
mana partikel q1, q2 dan Q berada. Tentukanlah
arah gaya listrik yang ditimbulkan q1 dan q2.

15. Penyelesaiannya
Gaya total pada Q adalah jumlah vektor dari gaya-
gaya yang ditimbulkan oleh q1 dan q2.
Muatan q1 menimbulkan gaya F1 pada muatan Q:
F1 pada Q = k |q1 Q|
r2
= (9,0 x 109
N.m2
/C2
)(2,0 x 10-6
C)(4,0 x 10-6
C)
(0,50 m)2
= 0,29 N

16. Penyelesaiannya
Cara paling mudah menjumlahkan vektor adalah
menggunakan komponen x dan y. Sudut α adalah
di bawah sumbu x, sehingga komponen gaya ini
diberikan oleh:
(F1 pada Q)x = (F1 pada Q) cos α = (0,29 N) 0,40 m
0,50 m
= 0,23 N
(F1 pada Q)y = -(F1 pada Q) sin α = -(0,29 N) 0,30 m
0,50 m
= -0,17 N

17. Penyelesaiannya
Sementara itu muatan q2 menimbulkan gaya F2 pada
muatan Q:
F2 pada Q = k |q2 Q|
r2
= (9,0 x 109
N.m2
/C2
)(4,0 x 10-6
C)(4,0 x 10-6
C)
(0,50 m)2
= 0,58 N
Komponen gaya F2 pada Q adalah:
(F2 pada Q)x = (0,58 N) cos α = 0,46 N
(F2 pada Q)y = (0,58 N) sin α = 0,34 N

18. Penyelesaiannya
Maka komponen gaya Ftotal pada Q adalah:
Fx = 0,23 + 0,46 = 0,69 N
Fy = -0,17 + 0,34 = 0,17 N
Fy Ftotal
= 0,71 N ϕ Fx
Arah Ftotal adalah pada sudut ϕ di atas sumbu x.
tan ϕ = Fy = 0,17 N = 0,25
Fx 0,69 N
o
22
yxtotal FFF +=

19. Medan Listrik
Medan listrik E adalah gaya listrik per
satuan muatan q0 yang dikerahkan pada
muatan tsb.
E = F0 / q0
q0 F0
E
F0 q0

20. Perhatian
 Gaya listrik pada sebuah benda yang
bermuatan ditimbulkan oleh medan
listrik yang diciptakan oleh benda
bermuatan lainnya
 Persamaan Fo = qo E dapat digunakan
hanya untuk mencari gaya listrik pada
sebuah muatan titik

21. Vektor Medan Listrik
E = 1 |q| besarnya medan listrik
4π∈0 r2
sebuah muatan titik
E = 1 qr vektor medan listrik
4π∈0 r2
muatan titik

22. Strategi Penyelesaian
Soal
Penghitungan Medan Listrik
Medan listrik adalah sebuah vektor,
sehingga medan total adalah jumlah vektor
dari medan individu
Vektor E yang dihasilkan oleh muatan titik
positif arahnya menjauhi muatan tersebut
Vektor E yang dihasilkan oleh muatan titik
negatif arahnya menuju muatan tersebut

23. Garis Medan Listrik

24. Garis Medan Listrik

25. Dipol Listrik
Sebuah dipol listrik adalah sepasang muatan
listrik yang besarnya sama, tetapi tandanya
berlawanan dan terpisah sejauh d.
p
d
ϕ d sin ϕ E

26. Momen Dipol Listrik
Hasil kali muatan q dan jarak d
dinyatakan sebagai momen dipol listrik p
dan besarnya p = qd
Arah vektor p adalah dari muatan negatif
menuju muatan positif.
Sebuah molekul air H2O
adalah contoh dipol listrik.

27. Gaya pada Dipol Listrik
Gaya F+ dan F- pada kedua muatan itu
mempunyai besar qE yang sama, tetapi
arahnya berlawanan, dan jumlah kedua
gaya itu sama dengan nol.
p F+= q E
d
ϕ d sin ϕ E
F- = -q E

28. Torsi pada Dipol
Listrik
Torsi dihitung terhadap pusat dipol. Jika ϕ
adalah sudut antara medan listrik dan
momen dipol, maka lengan tuas untuk
setiap F+ dan F- adalah (d /2) sin ϕ.
Torsi dari F+ dan F- mempunyai besar
yang sama, yakni (qE) (d /2) sin ϕ,
dan kedua torsi merotasikan dipol itu
dalam arah sama dgn perputaran jam.
Maka besar torsi netto sama dengan dua
kali besar torsi individu:
τ = (qE ) (d sin ϕ ) = pE sin ϕ

29. Kerja dW yang dilakukan oleh sebuah
torsi τ selama pergeseran dϕ yang sangat
kecil diberikan oleh persamaan:
dW = τ dϕ
Karena torsi tsb adalah dalam arah yang
semakin berkurang, τ = -pE sinϕ
sehingga
dW = -pE sinϕ dϕ
Energi Potensial
Dipol Listrik

30. Energi Potensial
Dipol Listrik
Dalam suatu pergeseran berhingga, kerja
total yang dilakukan pada dipol tsb adalah
Karena W = U1 – U2 , maka
U(ϕ) = - pE cos ϕ
Perkalian skalar p . E = pE cos ϕ
Sehingga energi potensial U (ϕ) = - p . E
1
2
1
2
φ
φ
φcospE-φcospEdφφsinpE-W ∫ ==

31. Contoh
Soal 3
Gaya dan torsi pada sebuah dipol listrik
Sebuah dipol listrik berada dalam medan listrik
homogen 5,0 x 105
N/C. Dipol tersebut adalah ±
1,6 x 10^-19 C dan terpisah sejauh 0,125 nm.
Carilah a) gaya netto yang dikerahkan medan pada
dipol; b) besar dan arah momen dipol listrik; c)
besar dan arah torsi; d) energi potensial sistem
-q
p 35o
145o
E
+q

32. Penyelesaian
Diketahui : q = 1,6 X 10-19
C; d = 0,125 X 10-9
m
E = 5,0 X 105
N/C; ϕ = 145o
Ditanya: a) F = ? b) p = ?
c) τ = ? d) U = ?
Jawab :
a) F+ = qE dan F- = -qE
Karena medan itu homogen maka gaya-gaya pada
kedua muatan itu sama besar dan berlawanan,
sehingga gaya total F = 0 N

33. Penyelesaian
b) p = qd = (1,6 X 10-19
C)(0,125 X 10-9
m)
= 2,0 X 10-29
C.m, dari negatif ke positif
c) τ = pE sinϕ
= (2,0 X 10-29
C.m)(5,0 X 105
N/C)(sin 145o
)
= 5,7 X 10-24
N.m, keluar dari bidang
d) U = -pE cosϕ
= -(2,0 X 10-29
C.m)(5,0 X 105
N/C)(sin 145o
)
-24