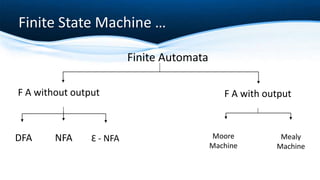
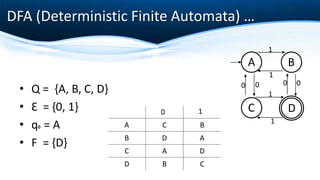
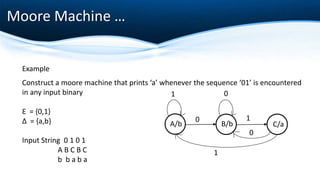
The document outlines key concepts of formalization machines, specifically focusing on finite state machines (FSM) including deterministic (DFA) and non-deterministic (NFA) automata, as well as Mealy and Moore machines. It explains their structures using tuples and provides examples to illustrate their functioning. Additionally, it discusses the transition functions, input alphabets, and output behaviors of these machines.

1. Formalization
Machines and States
D.K.S.Hasaranga & A.G.A.L.Dhanushka

2. Finite State Machine
• Symbol
 Ex: a, b, c, 0, 1, 2, 3, ….
• Alphabet – Collection of symbols (Ɛ)
 Ex: {a,b}, {0,1,2}
• String – Sequence of symbols
 Ex: a, b, 0, 1, aa, bb, ab, 01, ….

3. Finite State Machine …
• Language – Set of Strings
 Ex: Ɛ = {0,1}
L1 = set of all strings of length 2
= {00, 01, 10, 11}
L2 = Set of all strings of length 3
= {000, 001, 010, 011, 100, 101, 110, 111}
L3 = Set of all strings that begin with “0”
= {0, 00, 01, 000, 001, ……}
Finite
Infinite

4. Finite State Machine …
Finite Automata
F A without output F A with output
DFA NFA Moore
Machine
Mealy
Machine
Ɛ - NFA

5. DFA (Deterministic Finite Automata)
 It is the simplest model of the computation
 It has a very limited memory
Every DFA can define using 5 tuples. They are,
 Q = Set of states
 Ɛ = Inputs
 q0 = Start state or initial state
 F = Set of final states
 ƍ = Transition function from Q x Ɛ Q

6. DFA (Deterministic Finite Automata) …
• Q = {A, B, C, D}
• Ɛ = {0, 1}
• q0 = A
• F = {D}
A B
C D
1
1
1
1
00 0 0
A C B
B D A
C A D
D B C
0 1

7. NFA (Non-Deterministic Finite Automata)
Every NFA can define using 5 tuples. They are,
 Q = Set of states - {A, B}
 Ɛ = Inputs - {0, 1}
 q0 = Start state or initial state - A
 F = Set of final states - B
 ƍ = Transition function from Q x Ɛ ?
A B0
0, 1
• The machine can move to any combination of the states in the machine (the exact
state to which the machine moves cannot be determined).
• Hence, it is called Non-deterministic Automaton.
• As it has finite number of states, the machine is called Non-deterministic Finite
Machine or Non-deterministic Finite Automaton.
L = {Set of all strings ends with 0}

8. NFA (Non-Deterministic Finite Automata)
A B0
0, 1
ƍ = Transition function from Q x Ɛ 2Q
Little Exercise
A x 0 A , B , A B
A x 1 A
B x 0 ø
B x 1 ø
Possibilities = A,B,AB, ø
= 4
= 22

9. Mealy Machine
Every Mealy Machine can define using 6 tuples. They are,
 Q = Finite set of state
 Ɛ = Finite non-empty set of Input Alphabets
 Δ = The set of Output Alphabets
 ƍ = Transition function from Q x Ɛ Q
 λ = Output function : Ɛ x Q Δ
 q0 = Initial state / Start state
A Mealy Machine is an FSM whose output depends on the present state as well as the
present input.
a/0
a/1
b/0
b/0
b/1
A
B
a/0
C
L = {Set of all strings ends with aa or bb}

10. Moore Machine
Every Moore Machine can define using 6 tuples. They are,
 Q = Finite set of state
 Ɛ = Finite non-empty set of Input Alphabets
 Δ = The set of Output Alphabets
 ƍ = Transition function from Q x Ɛ Q
 λ = Output function : Q Δ
 q0 = Initial state / Start state
Moore machine is a finite state machine in which the next state is decided by the current
state and current input symbol. The output symbol at a given time depends only on the
present state of the machine.

11. Moore Machine …
A/b B/b
1
01
Example
C/a
0
Construct a moore machine that prints ‘a’ whenever the sequence ‘01’ is encountered
in any input binary
Ɛ = {0,1}
Δ = {a,b}
Input String 0 1 0 1
A B C B C
b b a b a
0 1