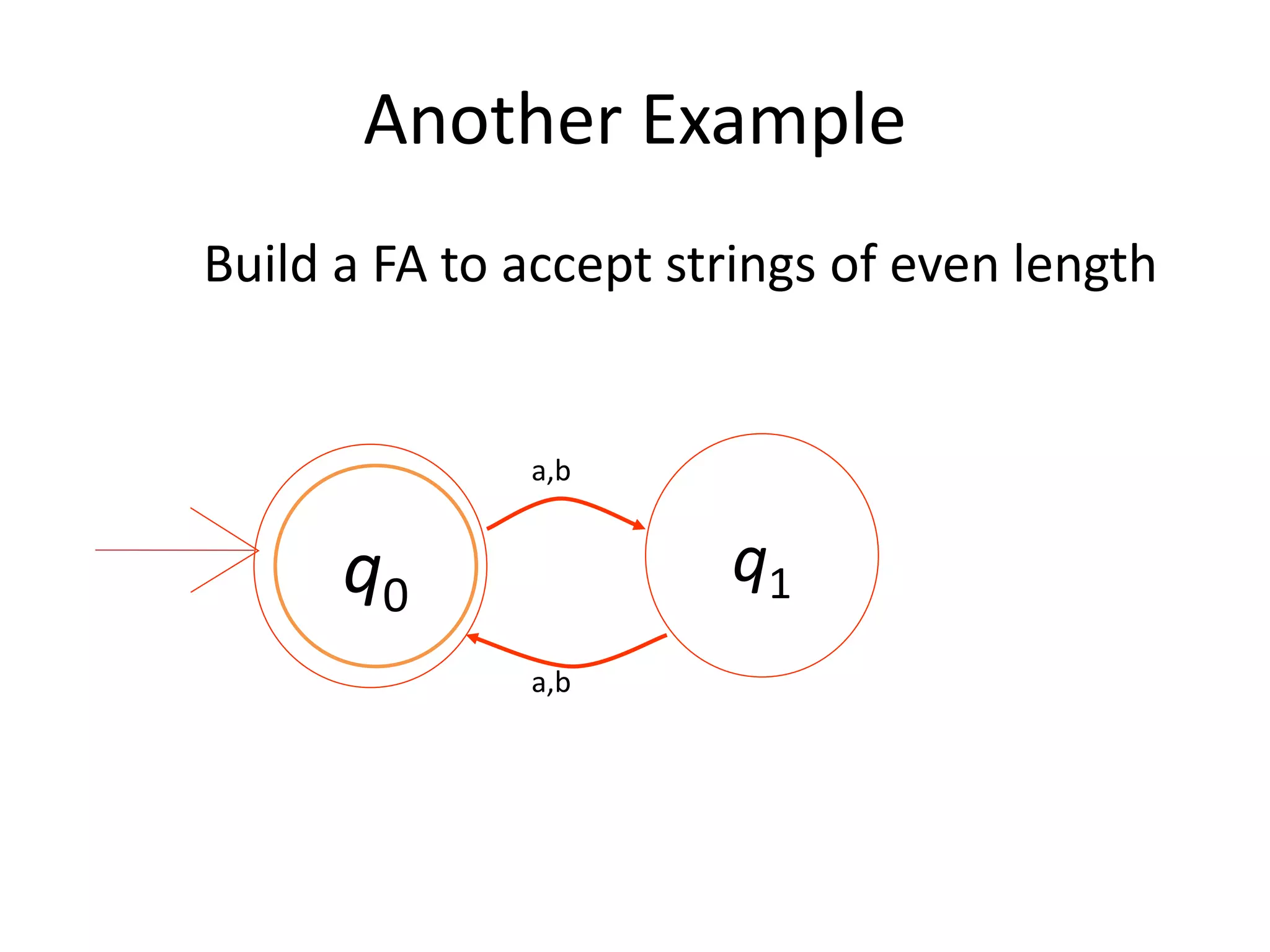
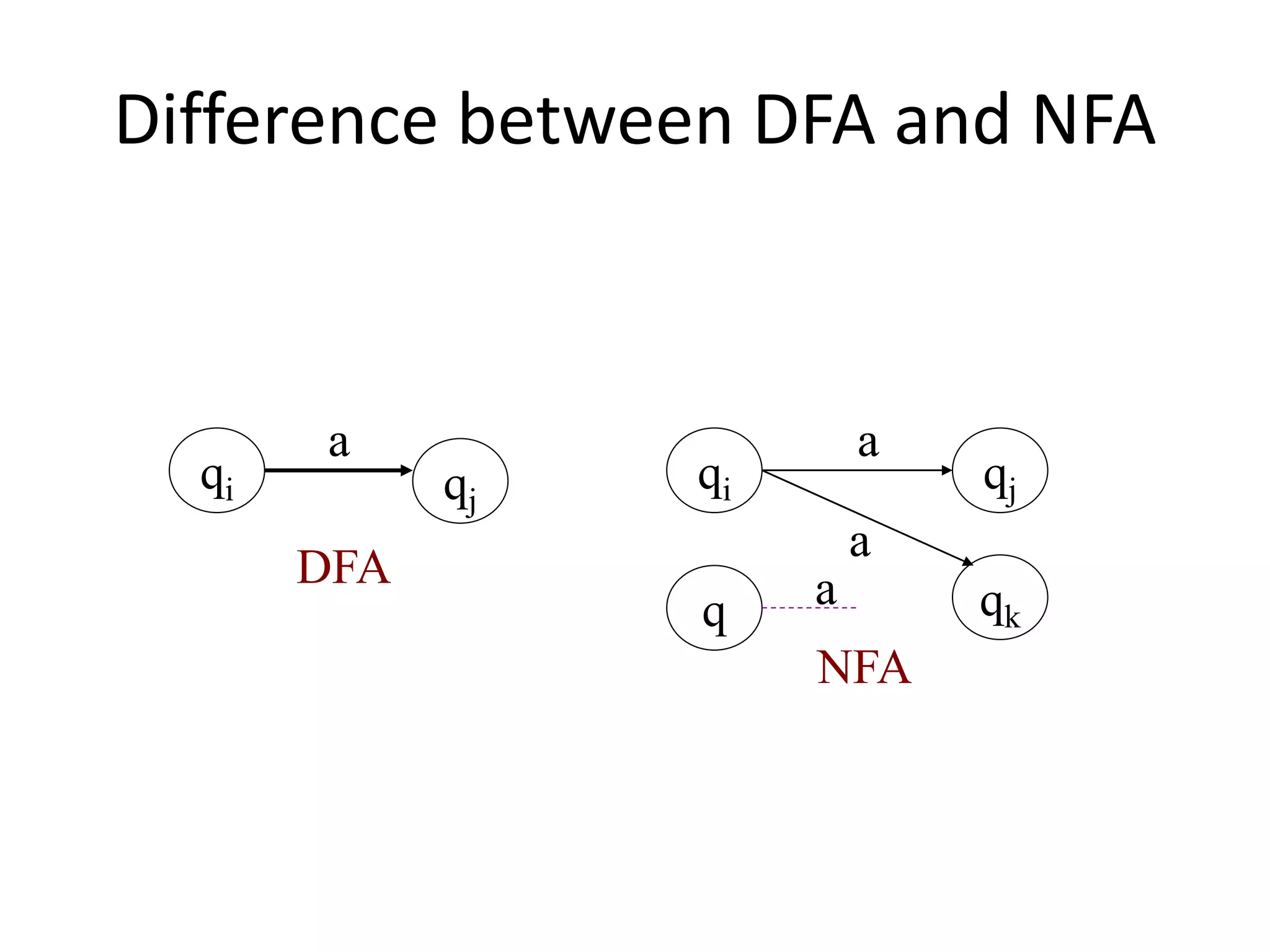
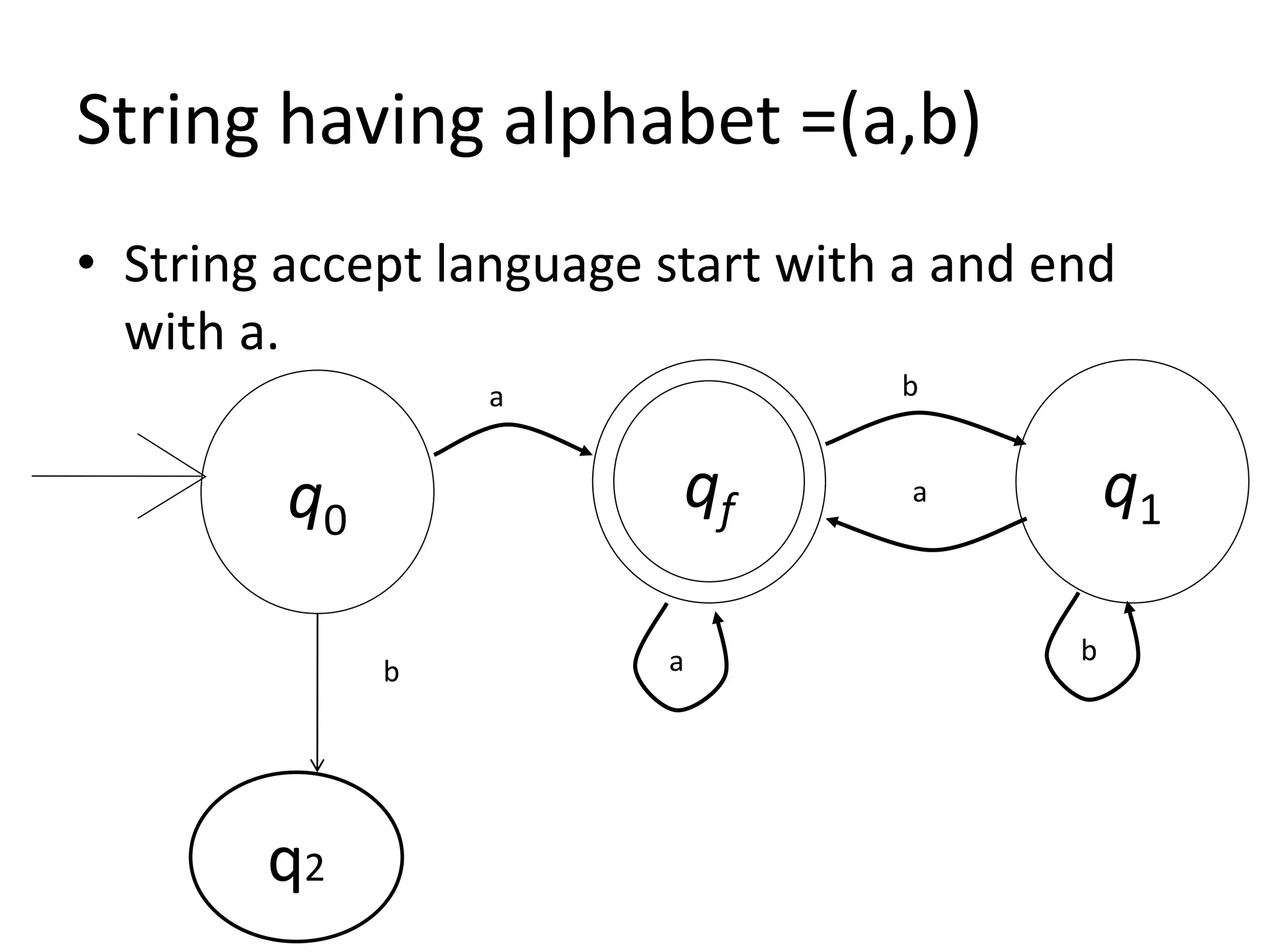
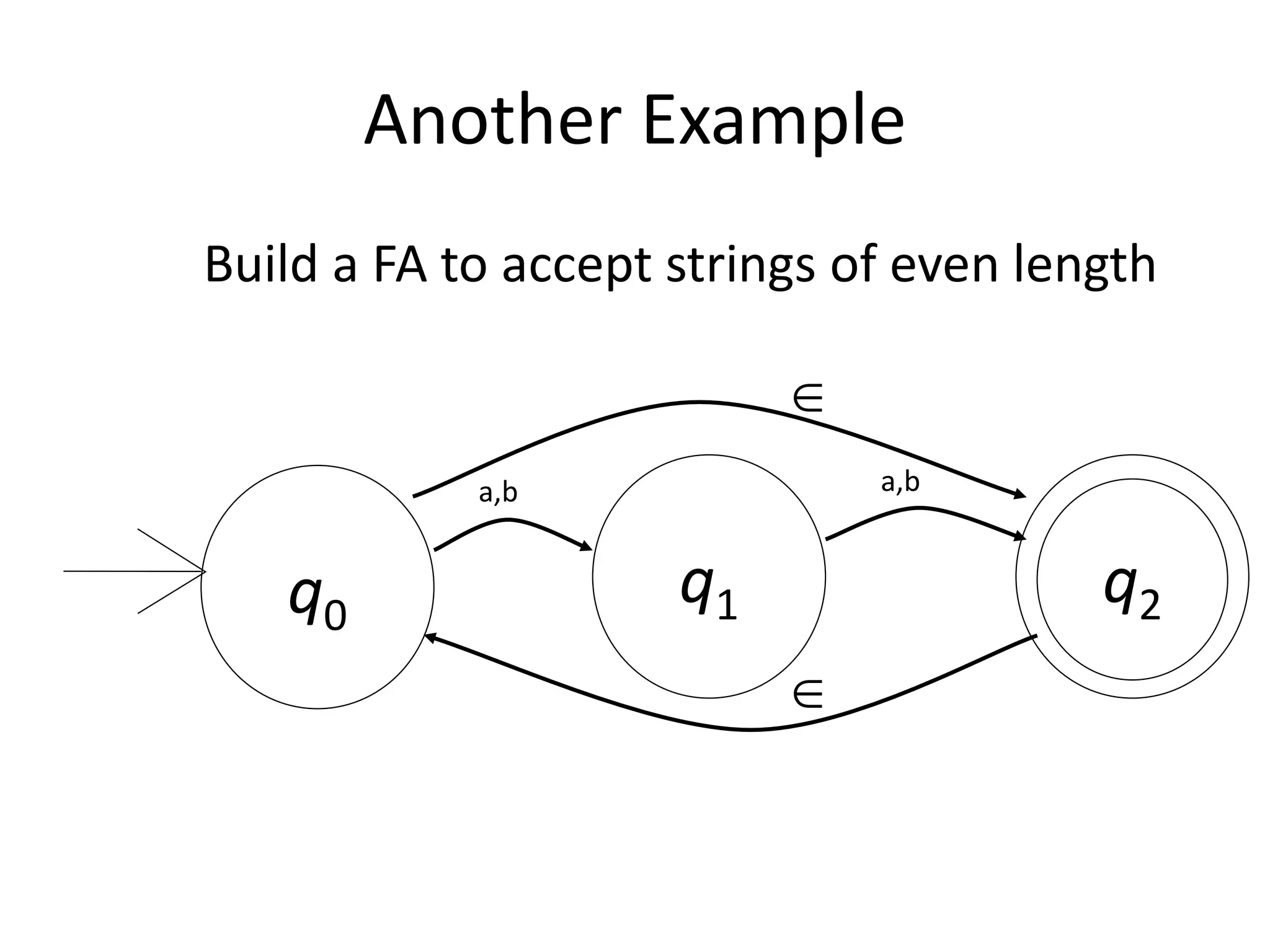
This document discusses finite automata, including: - Finite automata are machines that recognize patterns in input sequences. - There are two main types: deterministic finite automata (DFAs) and non-deterministic finite automata (NFAs). - DFAs have a single transition between states for each input, while NFAs may have multiple possible next states for each input.

1. Finite Automata
by
Manish Tadhiyal

2. Content
• Finite automata
• Types of finite automata
• Finite state diagram
• Deterministic finite automata(DFA)
• Example of DFA
• Non-deterministic finite automata(NFA)
• Example of NFA

3. Finite Automata
A finite automata (FA) is a simple idealized
machine used to recognize patterns within input
taken from some character set (or alphabet) C.
the job of an FA is to accept or reject a input
depending on whether the pattern defined by the FA
occurs in the input.

4. Types of finite automata
Finite automata without output
Deterministic finite automata
Non-deterministic finite automata
Finite automata with output
Mealy machine
Moore machine

5. Finite State Diagram
• A graphic representation of a finite automata
A finite state diagram is a directed graph, where
nodes represent elements in Q (i.e., states) and arrows
are characters in  such that:
qa qb Indicates: transmission between qa to qb
with a.
The initial state is marked with: >
The final state(s) are marked with:
a

6. Deterministic finite automata
For each pair of states and possible input
chars, there is a unique next state (as specified
by the transitions), then the FA is
deterministic finite automata.
That means the DFA follow single path with
single transmission.

7. Deterministic finite automata
Q:Finite set of states
: Finite Alphabet
d: Transition function
- a total function from Qx to Q
q0:Initial/Start State
F :Set of final/accepting state
),,,,( 0 FqQM d

8. Example
Set of strings over {a,b} that contain “bb”
q2q0 q1
a b
a
b
a
b
d a b
q0 q0 q1
q1 q0 q2
q2 q2 q2
}2{
},{
}2,1,0{
qF
ba
qqqQ



],1[],0[ *
qaabq 

9. Another Example
Build a FA to accept strings of even length
q1
a,b
a,b
q0

10. Non-Deterministic finite automata
For each pair of states and possible input
chars, there may be more then one next state
(as specified by the transitions), then the FA is
non-deterministic finite automata.
Conceptually, a nondeterministic FA can
follow many paths simultaneously.

11. Non-deterministic finite automata
(NDFA) or (NFA)
M = (Q,, , s, F) where
Q= Finite set of states
= Input alphabet
 = Q x  2^Q
s = Initial state
F = Final state

12. Difference between DFA and NFA
qi qj
qkq
qi qj
a a
a
DFA
NFA
a

13. String having alphabet =(a,b)
• String accept language start with a and end
with a.
q0
qf q1
a b
a
b a b
q2

14. Another Example
Build a FA to accept strings of even length
q0
q1 q2
a,b a,b

