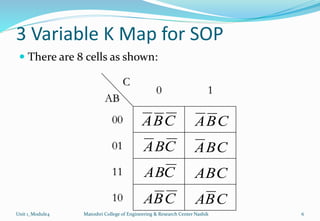
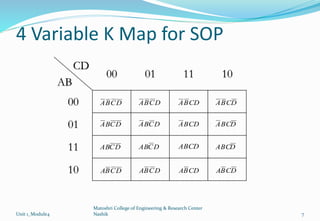
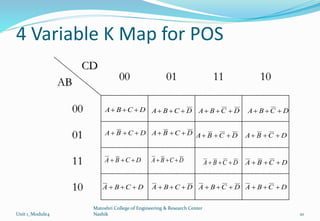
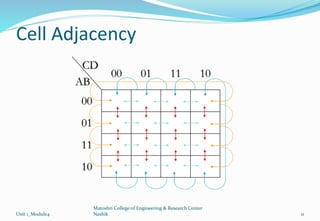
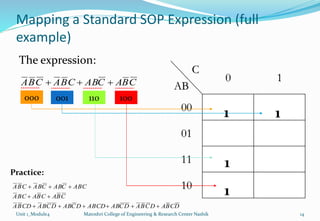
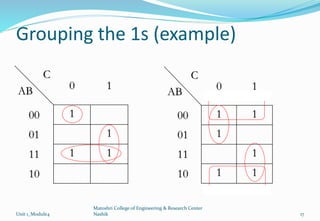
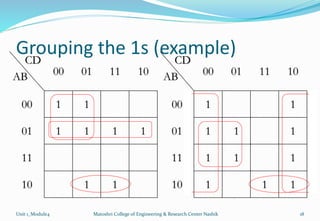
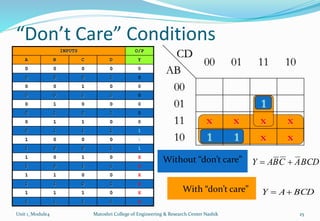
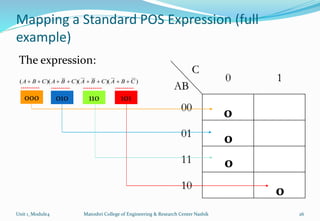
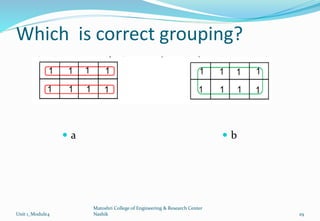
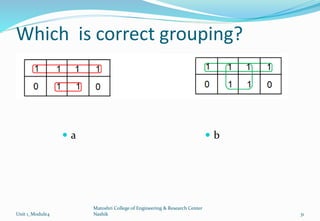
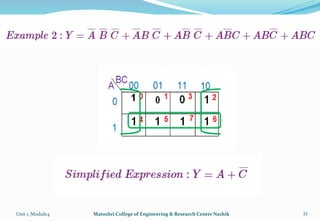
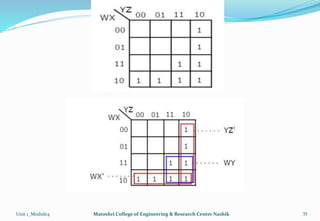
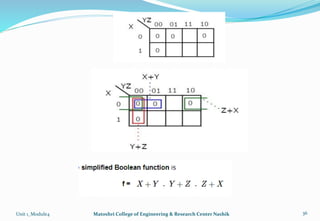
The document discusses Karnaugh maps and their use in simplifying Boolean expressions. It covers the basics of K-maps including their structure for 2, 3, and 4 variables and the rules for grouping cells to find the minimum expressions. Examples are provided to demonstrate mapping standard and nonstandard expressions to K-maps and grouping cells to arrive at simplified sums-of-products forms. The use of "don't care" conditions is also illustrated.

1. By
Mr. C.R.Shinde
Electrical Engineering Department
Matoshri College of Engineering & Research centre, Nashik

2. Unit 01 : Design of combinational circuit
M1:-Introductions
M2:- Booleans algebra, De-Morgan theory.
M3:- Karnaugh map: structure for two, three and four Variables, SOP and
POS form reduction of Boolean expressions by K-map.
M4:- Design of combinational circuits using Boolean expression and K-
map.
M5:- encoder, decoder, half and full adder.
Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 2

3. The Karnaugh Map
Unit 1_Module4 3
Matoshri College of Engineering & Research Center
Nashik

4. What is K-Map
• It’s similar to truth table; instead of being organized
(i/p and o/p) into columns and rows, the K-map is an
array of cells in which each cell represents a binary
value of the input variables.
• The cells are arranged in a way so that simplification of
a given expression is simply a matter of properly
grouping the cells.
• K-maps can be used for expressions with 2, 3, 4, and 5
variables.
Unit 1_Module4 4
Matoshri College of Engineering & Research Center Nashik

5. 2 Variable K Map for SOP
 There are 4 cells as shown:
B
A
0 1
0
1
B
A B
A
AB
B
A
Unit 1_Module4 5
Matoshri College of Engineering & Research Center Nashik

6. 3 Variable K Map for SOP
 There are 8 cells as shown:
C
AB
0 1
00
01
11
10
C
B
A C
B
A
C
B
A BC
A
C
AB ABC
C
B
A C
B
A
Unit 1_Module4 6
Matoshri College of Engineering & Research Center Nashik

7. 4 Variable K Map for SOP
CD
AB
00 01 11 10
00
01
11
10 D
C
B
A
D
C
AB
D
C
B
A
D
C
B
A
D
C
B
A
D
C
AB
D
C
B
A
D
C
B
A
CD
B
A
ABCD
BCD
A
CD
B
A
D
C
B
A
D
ABC
D
BC
A
D
C
B
A
Unit 1_Module4 7
Matoshri College of Engineering & Research Center
Nashik

8. 2 Variable K Map for POS
 There are 4 cells as shown:
B
A
0 1
0
1 B
A 
B
A 
B
A B
A
Unit 1_Module4 8
Matoshri College of Engineering & Research Center Nashik

9. 3 Variable K Map for POS
 There are 8 cells as shown:
C
AB
0 1
00
01
11
10
C
B
A 

C
B
A 

C
B
A 

C
B
A 

C
B
A 

C
B
A 

C
B
A 

C
B
A 

Unit 1_Module4 9
Matoshri College of Engineering & Research Center Nashik

10. 4 Variable K Map for POS
CD
AB 00 01 11 10
00
01
11
10
D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


D
C
B
A 


Unit 1_Module4 10
Matoshri College of Engineering & Research Center
Nashik

11. Cell Adjacency
CD
AB
00 01 11 10
00
01
11
10
Unit 1_Module4 11
Matoshri College of Engineering & Research Center
Nashik

12. K-Map SOP Minimization
 The K-Map is used for simplifying Boolean expressions to
their minimal form.
 A minimized SOP expression contains the fewest possible
terms with fewest possible variables per term.
 Generally, a minimum SOP expression can be implemented
with fewer logic gates than a standard expression.
Unit 1_Module4 12
Matoshri College of Engineering & Research Center Nashik

13. Mapping a Standard SOP Expression
 For an SOP expression in
standard form:
 A 1 is placed on the K-map
for each product term in
the expression.
 Each 1 is placed in a cell
corresponding to the value
of a product term.
 Example: for the product
term , a 1 goes in the
101 cell on a 3-variable
map.
C
B
A
C
AB
0 1
00
01
11
10
C
B
A C
B
A
C
B
A BC
A
C
AB ABC
C
B
A C
B
A1
Unit 1_Module4 13
Matoshri College of Engineering & Research Center Nashik

14. C
AB
0 1
00
01
11
10
Mapping a Standard SOP Expression (full
example)
The expression:
C
B
A
C
AB
C
B
A
C
B
A 


D
C
B
A
D
C
B
A
D
C
AB
ABCD
D
C
AB
D
C
B
A
CD
B
A
C
B
A
C
B
A
BC
A
ABC
C
AB
C
B
A
C
B
A











000 001 110 100
1 1
1
1
Practice:
Unit 1_Module4 14
Matoshri College of Engineering & Research Center Nashik

15. Mapping a Nonstandard SOP Expression
 Map the following SOP expressions on K-maps:
D
BC
A
D
AC
D
C
A
CD
B
A
D
C
B
A
D
C
B
A
C
AB
B
A
C
B
C
A
BC
C
AB
B
A
A











Unit 1_Module4 15
Matoshri College of Engineering & Research Center
Nashik

16. Grouping the 1s (rules)
1. A group must contain either 1,2,4,8,or 16 cells
(depending on number of variables in the
expression)
2. Each cell in a group must be adjacent to one or more
cells in that same group, but all cells in the group do
not have to be adjacent to each other.
3. Always include the largest possible number of 1s in a
group in accordance with rule 1.
4. Each 1 on the map must be included in at least one
group. The 1s already in a group can be included in
another group as long as the overlapping groups
include noncommon 1s.
Unit 1_Module4 16
Matoshri College of Engineering & Research Center Nashik

17. Grouping the 1s (example)
C
AB 0 1
00 1
01 1
11 1 1
10
C
AB 0 1
00 1 1
01 1
11 1
10 1 1
Unit 1_Module4 17
Matoshri College of Engineering & Research Center
Nashik

18. Grouping the 1s (example)
CD
AB 00 01 11 10
00 1 1
01 1 1 1 1
11
10 1 1
CD
AB 00 01 11 10
00 1 1
01 1 1 1
11 1 1 1
10 1 1 1
Unit 1_Module4 18
Matoshri College of Engineering & Research Center Nashik

19. Determining the Minimum SOP Expression from
the Map (example)
CD
AB
00 01 11 10
00 1 1
01 1 1 1 1
11 1 1 1 1
10 1
B
C
A
D
C
A
D
C
A
C
A
B 

Unit 1_Module4 19
Matoshri College of Engineering & Research Center Nashik

20. Determining the Minimum SOP Expression from
the Map (exercises)
C
B
A
BC
AB 

AC
C
A
B 

C
AB 0 1
00 1
01 1
11 1 1
10
C
AB 0 1
00 1 1
01 1
11 1
10 1 1
Unit 1_Module4 20
Matoshri College of Engineering & Research Center Nashik

21. Determining the Minimum SOP Expression from
the Map (exercises)
D
B
A
C
A
B
A 
 C
B
C
B
A
D 

CD
AB 00 01 11 10
00 1 1
01 1 1 1 1
11
10 1 1
CD
AB 00 01 11 10
00 1 1
01 1 1 1
11 1 1 1
10 1 1 1
Unit 1_Module4 21
Matoshri College of Engineering & Research Center Nashik

22. Practicing K-Map (SOP)
D
C
B
A
D
ABC
D
BC
A
D
C
B
A
CD
B
A
CD
B
A
D
C
AB
D
C
B
A
D
C
B
Q
C
B
A
C
B
A
C
B
A
BC
A
C
B
A
Q












)
2
(
)
1
(
C
A
B 
C
B
D 
Unit 1_Module4 22
Matoshri College of Engineering & Research Center Nashik

23. Mapping Directly from a Truth Table
I/P O/P
A B C X
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1
C
AB
0 1
00
01
11
10
1
1
1
1
Unit 1_Module4 23
Matoshri College of Engineering & Research Center
Nashik

24. “Don’t Care” Conditions
 Sometimes a situation arises in which some input
variable combinations are not allowed, i.e. BCD code:
 There are six invalid combinations: 1010, 1011, 1100, 1101, 1110,
and 1111.
 Since these unallowed states will never occur in an
application involving the BCD code  they can be
treated as “don’t care” terms with respect to their effect
on the output.
 The “don’t care” terms can be used to advantage on the
K-map (how? see the next slide).
Unit 1_Module4 24
Matoshri College of Engineering & Research Center Nashik

25. “Don’t Care” Conditions
INPUTS O/P
A B C D Y
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 X
1 0 1 1 X
1 1 0 0 X
1 1 0 1 X
1 1 1 0 X
1 1 1 1 X
CD
AB
00 01 11 10
00
01 1
11 x x x x
10 1 1 x x
BCD
A
C
B
A
Y 

BCD
A
Y 

Without “don’t care”
With “don’t care”
Unit 1_Module4 25
Matoshri College of Engineering & Research Center Nashik

26. C
AB
0 1
00
01
11
10
Mapping a Standard POS Expression (full
example)
The expression:
)
)(
)(
)(
( C
B
A
C
B
A
C
B
A
C
B
A 







000 010 110 101
0
0
0
0
Unit 1_Module4 26
Matoshri College of Engineering & Research Center Nashik

27. K-map Simplification of POS Expression
)
)(
)(
)(
)(
( C
B
A
C
B
A
C
B
A
C
B
A
C
B
A 









C
AB
0 1
00
01
11
10
0 0
0 0
0
C
B 
A
1
1
1
)
( C
B
A 
Unit 1_Module4 27
Matoshri College of Engineering & Research Center
Nashik

28. Which is correct grouping?
 a  b
Unit 1_Module4
Matoshri College of Engineering & Research Center
Nashik 28

29. Which is correct grouping?
 a  b
Unit 1_Module4
Matoshri College of Engineering & Research Center
Nashik 29

30. Which is correct grouping?
 a  b
Unit 1_Module4
Matoshri College of Engineering & Research Center
Nashik 30

31. Which is correct grouping?
 a  b
Unit 1_Module4
Matoshri College of Engineering & Research Center
Nashik 31

32. Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 32

33. Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 33

34. Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 34

35. Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 35

36. Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 36

37. Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 37

38. Thank you
Mr. C. R. Shinde
Electrical Engineering Department
Matoshri College of Engineering & Research centre, Nashik
If you have any query, ask me anytime on…… … .. . . .
cshinde58@gmail.com
chandrakant.shinde@matoshri.edu.in
9970031353
Unit 1_Module4 Matoshri College of Engineering & Research Center Nashik 38