Dokumen ini membahas tentang konsep dasar sistem Linear Time Invariant (LTI) dalam pengolahan sinyal digital. Materi meliputi analisis respon impulse, perilaku hubungan input-output melalui persamaan beda dan representasi diagram blok. Tujuan pembelajaran adalah agar mahasiswa mampu menjelaskan dan mengimplementasikan sistem LTI.

1. Bab 4 Sistem Linear Time
Invariant
Prodi Teknik Telekomunikasi, Departemen Teknik Elektro
Politeknik Elektronika Negeri Surabaya
Penyusun:
Tri Budi Santoso
Miftahul Huda
Pengolahan Sinyal Digital

2. Tujuan Instruksional:
• Mahasiswa mampu menjelaskan konsep dasar
system linear time invariant (LTI), representasi
system LTI dalam bentuk persamaan beda,
inplementasi system LTI dalam bentuk diagram
blok.

3. Outline:
1. Konsep Sistem Linear Time Invariant
2. Respon Impulse Sistem LTI
3. Perilaku Hubungan Input-Output pada
Persamaan Beda
4. Representasi Diagram Blok

4. 4.1. Konsep Sistem Linear Time Invariant
• Sistem Linear memiliki sifat bahwa ouputnya akdalah linear dengan
input terkait. Sehingga jika input x1(t)menghasilkan output y1(t) dan input
x2(t) menghasilkan output y2(t), selanjutnya kombinasi linear pada kedua
input tersebut akan menghasilkan kombinasi linear pada kedua output
tersebut.
• Input (x1(t) + x2(t)) akan menghasilkan output (y1(t) + y2(t)). Selanjutnya,
input (a1x1(t) + a2x2(t)) akanmenghasilkan output (a1y1(t) +a2y2(t)) untuk
suatu konstanta a1 dan a2.
• Sistem Time-invariant adalah sistem di mana output untuk sebuah
input partikular tidak akan berubah tergantung pada waktu ketika input
terebut diaplikasikan.
• Sebuah sistem time-invariant yang memasukkan signal x(t) dan
menghasilkan output y(t), ketika eksitasi sinyal x(t + s), akanmenghasilkan
sebuah output y(t) dengan bentuk time tergeser (time-shifted) y(t + s).

5. Analisa atau pencirian sistem LTI:
Analisa atau pencirian sistem LTI dapat dilakukan dengan
berbagai cara:
• Respon Impulse
• Hubungan Input/Output pada pers. beda / pers. differensial
• Representasi diagram blok

6. 4.2. Analisa Sistem LTI dengan Melihat
Respon Impulse
Ketika diberi sinyal impulse, akan diperoleh output yang
diekpresikan sebagai superposisi terbobot dan time-shifted.
Discrete time system
Concolution Sum
Continouse time system
Concolution Integral
Sinyal Input
(Impulse)
Sinyal Output
(Respon Impulse)
Sistem

7.  Convolution Sum
• Misal sebuah sinyal x[n] dikalikan dengan sekuen impulse d[n]
x[n]d[n] = x[0]d[n]
• Bila digeneralisir menjadi product of x[n] dan suatu time-
shifted impulse sequence, untuk mendapatkan:
x[n]d[n-k] = x[0]d[n-k]
n time indek, x[k]
suatu nilai spesifik pada x[n] untuk waktu k. Maka ekpresi x[n]:




k
knkxny ][][][ d

8. • Jika dikaitkan dengan operator H pada sistem yang diberi input x[n], maka:
• Sifat linearity bisa menukar posisi operator H
• Bisa juga dilanjutkan sebagai:
Persamaan ini menggambrkan respon lengkap yang mencirikan perilaku
input-output, dan merupakan sifat fundamental dari sistem linear.
    
   











knnxH
nxHny
d
      


 knnxHny d
      


 knHnxny d
time-shifted
weighted sum
impulse

9. • Output uyang dikaitkan dengan time-shifted impulse adalah
suatu time-shifted version dari output terkait dengan input
impulse. Sehingga:
• Maka persamaan tsb bisa dituliskan ulang sbg:
• Yang juga punya bentuk umum:
    
    nHnh
knhknH
d
d


Respon impulse
sistem LTI
     


 knhkxny
       


 knhkxnkx d

10. Contoh 1:
Suatu sistem memiliki hubungan input-output sebagai:
Dapatkan output sistem untuk input sbb:
Solusi :
Diawali dengan x[n]= d[n], akan diperoleh:....
     1
2
1
 nxnxny
 











lainyangn
n
n
n
nx
;0
2;;2
1;4
0;2
 










lainyangn
n
n
nh
;0
1;
2
1
0;1
..0 1 2 3 4 5 n
1
1/2

11. Cara sederhana kita juga memiliki (dari input x[n])
x[n] sebagai weighted sum of time-shifted impulse
Output bisa dihitung sbb:
Dan bis a dituliskan sbb:
       22142  nnnnx ddd
-1 0 1 2 3 4 5 n
2
4
x[n]
-2
     
     
     
     
      032144
11022133
02212122
51402111
212100





xxy
xxy
xxy
xxy
xxy
 

















4;0
3;1
2;0
1;5
0;2
0;0
n
n
n
n
n
n
ny
-1 0 1 2 3 4 5 n
2
5
y[n]
-1

12.  Convolution Integral
Ekpresikan suatu continouse-time signal sebagai weighted superposition dari
suatu time-weighted impulse:
Tetapkan operator H:
Dengan lenearity property of the sum:
Kita definisikan h(t)=H{d(t)}, maka untuk sistem time-invariant bisa diperoleh
hubungan:
      


 d dtHxty
         


 d dtHxtxHty
     


 d dtxtx
    d  thdtH

13. h(t)
t0
x() d(t-)
t
x(2)
2
h(t)
LTI
t0
x()h(t)
x()
Jika:
Outputnya:
Dalam bentuk umum juga dikenal sbg:
     


  dthxty
       


  dthxthtx

14. Contoh:
t
u(t-1)
0 1 2 3 4....
....
t
u(t-3)
0 1 2 3 4....
....
t
x(t) = u(t-1)-u(t-3)
0 1 2 3 4....
....
Input: x(t) = u(t1)  u(t  3)

15. t0 1 2 3 4....
....
2
1
t
h(t) = u(t) - u(t-2)
0 1 2 3 4....
....
Dapatkan: )()( thtx 



  dthtxthtxty )().()()()(
Hasilnya kurang lebih:












5;0
53;5
31;1
1;0
)(
t
tt
tt
t
ty

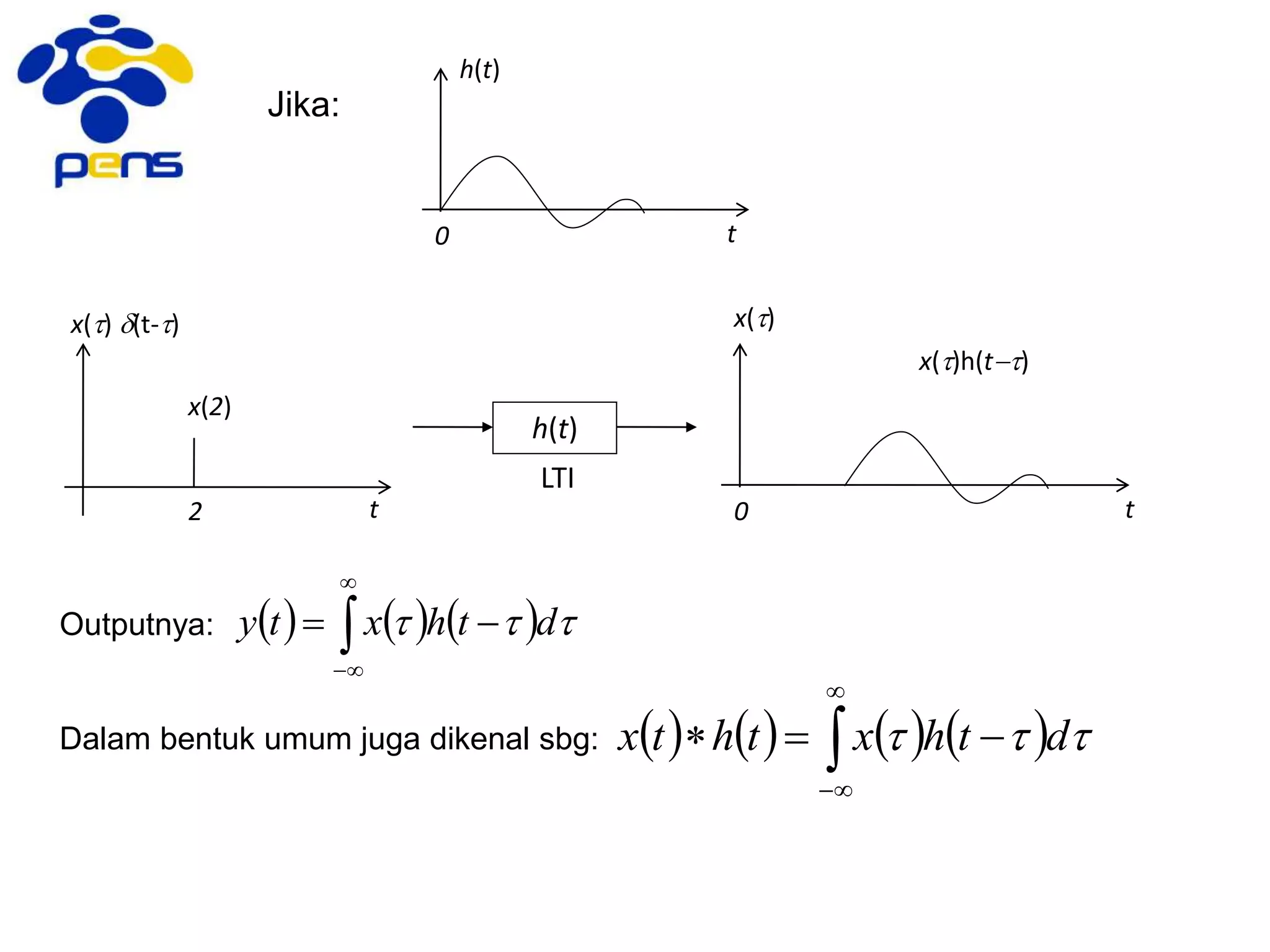
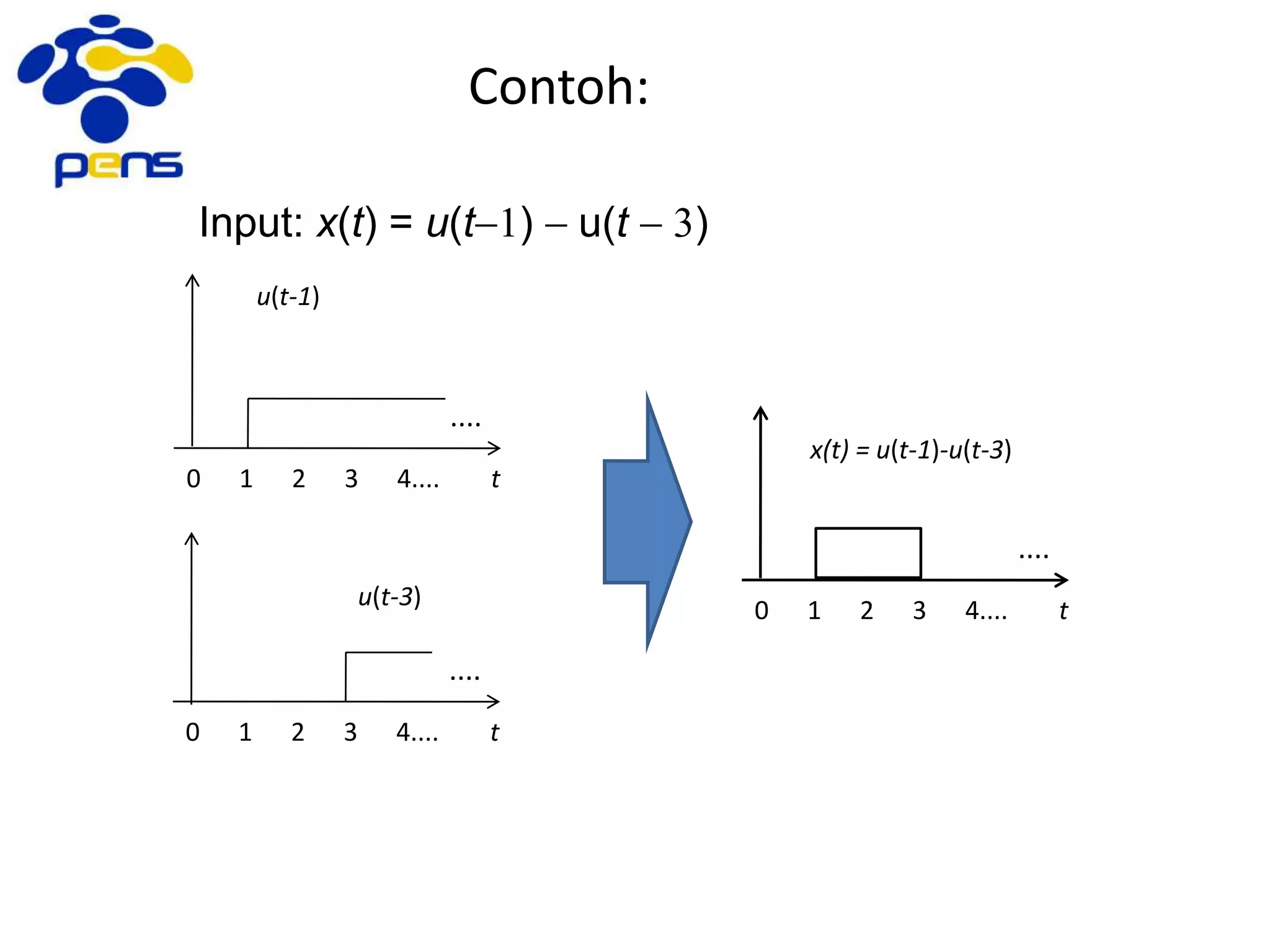
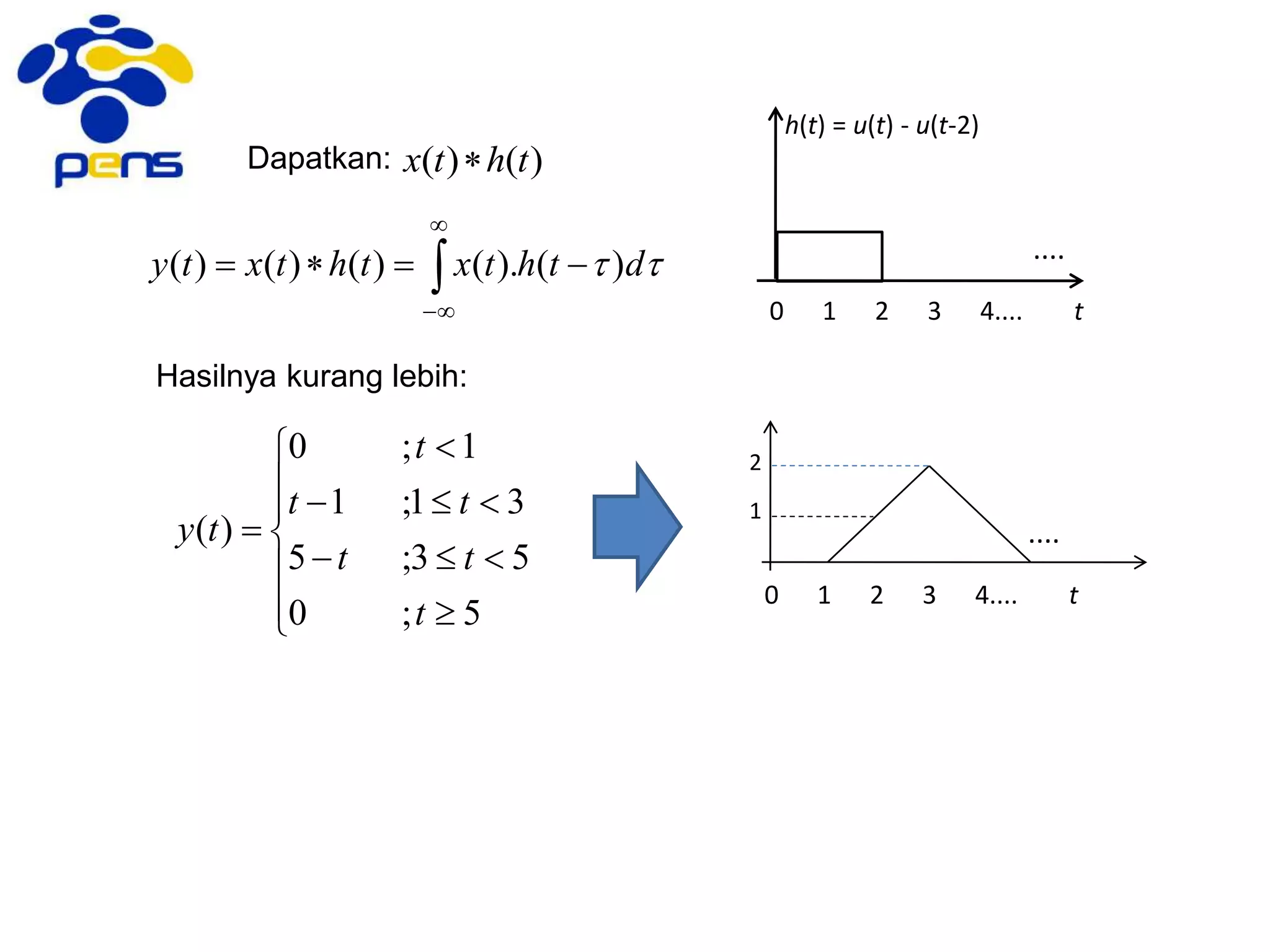
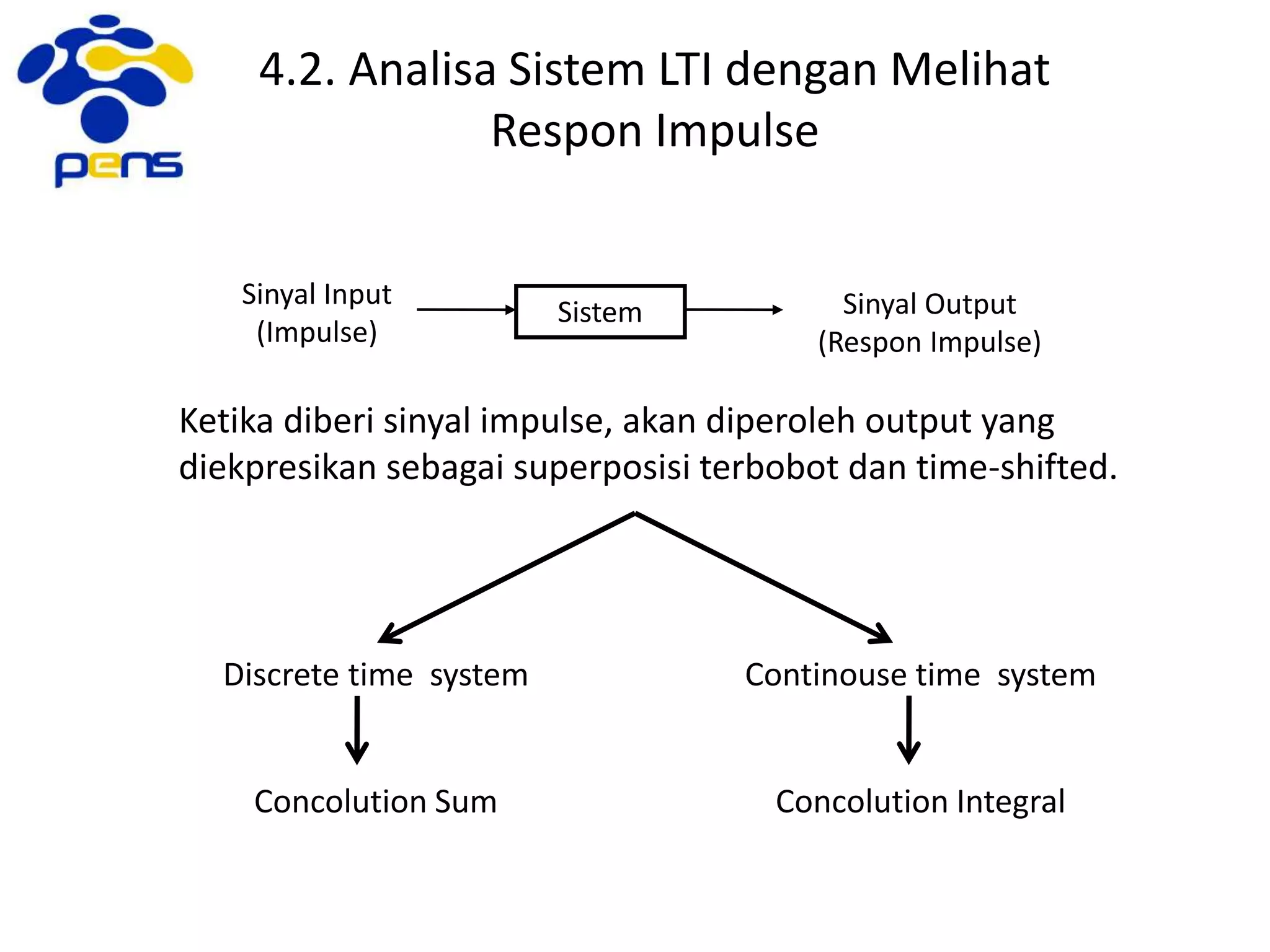
16. 4.3. Perilaku Hubungan Input-Output
pada Persamaan Beda
Hubungan input-output pada sistem LTI bisa direpresentasikan dalam bentuk:
• Persamaan beda discrete time
• Persamaan differensial continuous time
Bentuk umum persamaan beda:
di mana ak dan bk adalah koefisien-koefisien pada sistem, dan x[n] adalah
input, sedang y[n] adalah output.
Bentuk derivative:
Digantikan sebagai bentuk operator delay.
M dan N menyatakan orde pada persamaan beda, yang
merepresentasikan jumlah energy storage device di dalam sistem.
    

M
k
k
N
k
k knxbknya
00
       knxtx
dt
d
knyty
dt
d
k
k
k
k


17. Contoh:
Persamaan diferensial yang merepresentasikan sistem tsb:
Input x(t) = v(t)
Output arus  y(t)
Maka:
Diferensiasi kedua sisi persamaan memberikan:
Ini merupakan persamaan beda orde N=2. Jika dikaitkan dengan persamaan beda
bisa direpresentasikan sbb:
       

t
txdy
C
ty
dt
d
LtRy 
1
       tx
dt
d
ty
dt
d
Lty
dt
d
Rty
C
 2
2
1
       122
1
 nxnLynRyny
C

18. 4.4. Representasi Diagram Blok
• Diagram blok: suatu interkoneksi operasional dasar yang
memberikan perlakuan pada sinyal input.
• Dibanding impulse response dan persamaan beda/diff, maka
representasi diagram blok mampu memberi gambaran yang
lebih detail pada sistem LTI, dan dapat digunakan sebagai
dasar dalam implementasi software atau hardare

19. 3 elemen dasar operasional pada diagram blok:
• Operasi perkalian (skalar)
• Addition
• Integrasi (waktu kontinyu)
Untuk waktu diskrit, operasi integral bisa dikaitkan dengan pergeseran atau delay (diferensial)
       ncxnyatautcxty 
     
     nwnxny
atau
twtxty


x(t)
x[n]
y(t)
y[n]
c
   nxatautx
   nwatautw
   nyatauty

x(t) y(t) x[n] x[n-1]
D
x[n] x[n-1]
z-1

20. contoh:
Suatu sistem dinytakan dalam persamaan beda sbb:
Sementara:
Maka persamaan tsb dapat dinyatakan sbg:
Di dalam bentuk diagram blok dapat digambarkan sbb:
       21 210  nxbnxbnxbnw
Gambarkan diagram
bloknya…       21 21  nyanyanwny
           
           2121
2121
21021
21210


nxbnxbnxbnyanyany
nyanyanxbnxbnxbny
x[n]
x[n-1]
D
b0
x[n-1]
D
b1
b2
D
D
a1
a2
y[n]
y[n-1]
y[n-1]
Direct Form I

21. Atau bisa disederhanakan lagi
x[n]
D
b0
D
-a1
-a2
b1
b2
y[n]

22. Soal:
1. Berikan diagram blok yang merepresentasikan sistem LTI sbb:
a)
b)
         122
3
1
1
2
1
 nxnxnynyny
       12
4
1
1
2
1
 nxnynyny