1. The document discusses econometrics and the linear regression model. It outlines the methodology of econometric research which includes stating a theory or hypothesis, specifying a mathematical model, specifying an econometric model, obtaining data, estimating parameters, hypothesis testing, forecasting, and using the model for policy purposes. 2. It provides an example of specifying Keynes' consumption function as the mathematical model C= β1 + β2X where C is consumption and X is income. For the econometric model, an error term is added to allow for inexact relationships. 3. Assumptions of the classical linear regression model are discussed including the error term being uncorrelated with X, having a mean of zero,

1. ECONOMETRICS
-

2. Module-I: Linear Regression model
• Nature,
• Meaning and scope of econometrics;
• Methodology of econometric research;
• Basic concepts of estimation; desirable properties of estimators,
• Simple Linear Regression Model: assumptions, estimation (through OLS
method).
• Gauss- Markov Theorem, interpretation of regression coefficients.

3. Methodology of econometric research
How do econometricians proceed in their analysis of an economic problem?
That is, whatis their methodology? So methodology is in this steps:
1. Statement of theory or hypothesis.
2. Specification of the mathematical model of the theory.
3. Specification of the statistical, or econometric, model.
4. Obtaining the data.
5. Estimation of the parameters of the econometric model.
6. Hypothesis testing.
7. Forecasting or prediction.
8. Using the model for control or policy purposes.

4. 1. Statement of Theory or Hypothesis
Keynes stated:
The fundamental psychological law . . . is that men [women] are disposed,
as a rule and on average, to increase their consumption as their income
increases, but not as much as the increase in their income.10
In short, Keynes postulated that the marginal propensity to consume
(MPC), the rate of change of consumption for a unit (say, a dollar) change in
income, is greater than zero but less than 1.

5. Meaning and scope of econometrics
Econometrics, the result of a certain outlook on the role of economics, consists
of the application of mathematical statistics to economic data to lend empirical
support to the models constructed by mathematical economics and to obtain
numerical results.
SCOPE
Why a Separate Discipline?
econometrics is an amalgam of economic theory, mathematical economics,
economic statistics, and mathematical statistics.
Economic theory makes statements or hypotheses that are mostly qualitative
in nature.
The main concern of mathematical economics is to express economic theory
in mathematical form (equations) without regard to measurability or empirical
verification of the theory.
Economic statistics is mainly concerned with collecting, processing, and
presenting economic data in the form of charts and tables.

6. 2. Specification of the Mathematical Model of
Consumption
Although Keynes postulated a positive relationship between consumption
and income, he did not specify the precise form of the functional relationship
between the two. For simplicity, a mathematical economist might suggest
the following form of the Keynesian
consumption function:
Y = β1 + β2X 0 < β2 < 1
where Y = consumption expenditure and X = income, and where β1 and β2,
known as the parameters of the model, are, respectively, the intercept and
slope coefficients.

7. Consumption function

8. 3. Specification of the Econometric Model
of Consumption
The purely mathematical model of the consumption function is of limited
interest to the econometrician, for it assumes that there is an exact or
deterministic relationship between consumption and income. But relationships
between economic variables are generally inexact.
To allow for the inexact relationships between economic variables, th
econometrician would modify the deterministic consumption function
Y = β1 + β2X + u
where u, known as the disturbance, or error, term, is a random (stochastic)
variable that has well-defined probabilistic properties. The disturbance term u
may well represent all those factors that affect consumption but are not taken
into account explicitly.
It is an example of a linear regression model.

9. 4. Obtaining Data
To estimate the econometric model given in Eq. (I.3.2), that is, to obtain the
numerical values of β1 and β2, we need data.
TYPES OF DATA
Time Series Data
A set of observations that a variable takes at different times, such as daily
(e.g., stock prices), weekly (e.g., money supply), monthly (e.g., the
unemployment rate), quarterly (e.g., GDP), annually (e.g., government
budgets), quinquenially or every five years (e.g., the census of manufactures),
or decennially or every ten years (e.g., the census of population).

10. .
Cross-Section Data
Data on one or more variables collected at the same point in time.
Examples are the census of population conducted by the Census Bureau every
10 years, opinion polls conducted by various polling organizations, and
temperature at a given time in several places.
Panel, Longitudinal or Micro-panel Data
Combines features of both cross-section and time series data.
Same cross-sectional units are followed over time.
Panel data represents a special type of pooled data (simply time series, cross-
sectional, where the same cross-sectional units are not necessarily followed over
time).

11. Basic concepts of estimation

12. STATISTICS
• A statistic is a function of only the value of random sample
• X1,X2……….Xn

13. Properties of estimation
• 1.Unbaised

14. Continued
• Minimum variance : Minimum variance of all the unbaised
estimators, the best estimator has a sampling distribution with
the smallest standard error.
• In statistics a minimum-variance unbiased estimator (MVUE)
/uniformly minimum variance unbiased estimator (UMVUE)
is an unbiased estimator that has lower variance than any
other unbiased estimator for all possible values of the
parameter.

15. Conitued
• Minimum mean square error- it is defined as the expected value of
squared difference of the estimator around the true population
parameter.
• Efficiency : some econometrics equate efficiency with minimum MSE
of estimator, other define efficiency only in the context of asymptotic
properties rather that finite sample properties, other consider as
estimator to be efficient if it is unbaised and at same time has
minimum varience.

16. Estimation
• Estimator: Statistic whose calculated value is used to
estimate a population parameter, theta
• Estimate: A particular realization of an estimator,
Types of Estimators:
• point estimate: single number that can be regarded as the
most plausible value of theta.
The aim is to obtain a singlr value which is best guess of the
parameter of interest.

17. Continued
• interval estimate: a range of numbers, called a confidence interval
indicating, can be regarded as likely containing the true value of
theta.
• In The interval estimation the object is to obtain interval within
which the true value of parameter may be said to lie with some given
level of probability which expresses the confidence we have that the
value lies within the stipulated range.

18. Simple Linear Regression Model
• We consider the modeling between the dependent and one independent variable. When
there is only one independent variable in the linear regression model, the model is
generally termed as simple linear regression model. When there are more than one
independent variables in the model, then the linear model is termed as the multiple linear
regression model.
• Consider a simple linear regression model
• where y is termed as the dependent or study variable and X is termed as independent
or explanatory variable.
• The terms beta0 and beta1 are the parameters of the model. The parameter is termed as
intercept term and the parameter is termed as slope parameter. These parameters are
usually called as regression coefficients.

19. CONTINUED
• The unobservable error component accounts for the failure of data to lie on the straight line and
represents the difference between the true and observed realization of y. This is termed as
disturbance or error term. There can be several reasons for such difference, e.g., the effect of all
deleted variables in the model, variables may be qualitative, inherit randomness in the observations
etc. We assume that is observed as independent and identically distributed random variable with
mean zero and constant variance . Later, we will additionally assume that error components is
normally distributed.

20. Assumption
• in regression analysis our objective is notonly to obtain ˆ β1 and ˆ β2
but also to draw inferences about the true β1 and β2.
• We have to see how close Yˆi is to the true E(Y | Xi ).
So we have ot only show it equation but also provide some assumptions
about how Yi generated.
• Reason – Yi = β1 + β2Xi + ui , we see that Yi depend on Xi and ui
.So firstly we have to specific about them then about parameters.
The Gaussian, standard, or classical linear regression model (CLRM),
which is the base of most econometric theory, makes 8 assumptions.

21. Assumption 1.
• Linear Regression Model: The regression model is linear in the
parameters though it may or may not be linear in the variables.
Yi = β1 + β2 Xi + ui
• this model can be extended to include more explanatory variables
Y = B1² + B2²X + u. = it is not Linear Regression model
Y = B1 + B2X ² + u :it is linear regression model

22. Assumption 2
• Fixed X Values or X Values Independent of the Error Term:
It means that there should not relation between u and explanatory
variables.
cov (Xi , ui) = 0.

23. Assumption 3
• Zero Mean Value of Disturbance ui: E(ui |Xi) = Or, if X is nonstochastic,
E(ui) = 0 the mean value of ui conditional upon the given Xi is zero.

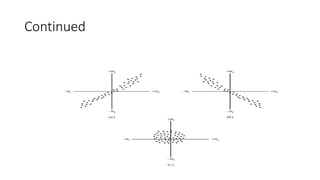
24. Assumption 4
• Homoscedasticity or Constant Variance of ui:
• var (ui) = E[ui − E(ui |Xi)]2
= E(u2i|Xi), because of Assumption 3
= E(u2i), if Xi are nonstochastic
= σ2
It means equal (homo) spread
(scedasticity) or equal variance

25. Continued
• In contrast, where the conditional variance of the Y population varies
with X. This situation is known appropriately as heteroscedasticity, or
unequal spread, or variance. Symbolically, in this situation,can be
written as var (ui |Xi) = σ2i.

26. Assumption 5
• No Autocorrelation between the Disturbances:
• Given any two X values in equation, Xi andXj (i & j), the correlation
between any two ui and uj (i & j ) is zero. In short, the observations are
sampled independently. Symbolically, cov(ui, uj |Xi, Xj) = 0
• cov(ui, uj) = 0, if X is nonstochastic ,( i and j are two different observations
& cov means covariance).
• We can also say that there is no serial correlation, or no autocorrelation
• u’s are negatively correlated when there is negative relation between
them and negatively sloped.
• u’s are positively correlated when there is positive relation between
them and positively sloped.

27. Continued

28. Assumption 6 & 7
• The Number of Observations n
Must Be Greater than the
Number of Parameters to Be
Estimated: the number of
observations must be greater
than the number of explanatory
variables.
• The Nature of X Variables: The X
values in a given sample must
not all be the same . Technically,
var (X) must be a positive
number. Furthermore, there can
be no outliers in the values of
the X variable, that is, values
that are very large in relation to
the rest of the observations.

29. Assumption 8
• There is no perfect multicollinearity:
It means that there are no perfect linear relationship among
explanatory variables .
Example : health : b1+ b2education+ b3consumption+b4 income + u
Here income effected health , education , consumption . So it shows
the multicollinearity.

30. Gauss- Markov Theorem (Properties of
Least-Squares Estimator)
• Given the assumptions of the classical linear regression model, the
least squares estimates possess some ideal or optimum properties.
These properties are contained in the well-known Gauss–Markov
theorem.
• Sometimes this theorem is referred to as the BLUE theorem , where
BLUE mean best linear unbaised estimator and lieast suares
estimators are referred to as BLUE.